Edelstein-Keshet L. Mathematical Models in Biology
Подождите немного. Документ загружается.


66
Discrete Processes
in
Biology
Typical population data
are
17.
This problem pursues
further
the
topic
of
blood
COa and
ventilation volume
first
described
in
Section
1.9 and
problem
16 of
Chapter
1.
There
we
studied
a
linear
model
for the
process;
we now
examine
a
nonlinear extension,
(a)
Whereas
in
problem 1.16
we
assumed that
the
amount
of CO2
lost,
£(V
n
, C
n
),
was
simply proportional
to V
n
and
independent
of C
n
, let us
now
consider
the
case
in
which
Explain
the
biological
difference between these distinct hypotheses.
(b)
Further assume that
the
ventilation volume
V
n
+\
is
simply proportional
to
C
n
, so
that
as
before. Write down
the
system
of
(nonlinear) equations
for C
n
and V
n
.
(c)
Show that
the
steady state
of
this system
is
and
determine
its
stability.
(d) Are
oscillations
in V
n
and C
n
possible
for
certain ranges
of the
parame-
ters?
(e) Now
consider
a
more realistic model (based
on
Mackey
and
Glass, 1977,
1978). Assume that
the
sensitivity
of
chemoreceptors
to CO2 is not
linear
but
rather sigmoidal, i.e.,
where
Further suppose that
with
t£(V
n
,
C
n
) as
before. Write down
the
system
of
equations,
and
show
that
it can be
reduced
to the
following single equation
for C
n
:
(f)
Sketch Sf(C)
as a
function
of C for € = 0, 1, 2. The
integer
€ can be de-
scribed
as a
cooperativity
parameter. (For
£ > 1 the
binding
of a
single
CO2
molecule
to its
chemoreceptor
enhances additional binding; this type
of
kinetic assumption
is
described
in
Chapter
7.)
(g)
Determine what equation
is
satisfied
by the
steady states
C
n
and V
n
.
(h) For € = 1 find the
value
of the
physiological steady state(s). Give
a
con-
dition
for
their
stability,
(i)
Investigate
the
model
by
writing
a
computer simulation
or by
further
analysis.
Are
oscillations possible
f
or € = 1 or for
higher
€
values?
Comment:
After
thinking about this problem,
you may
wish
to
refer
to the
arti-
cles
by
Mackey
and
Glass. Their model combines differential
and
difference
equations
so
that
the
details
of the
analysis
are
different.
See
references
in
Chapter
1.

Nonlinear
Difference
Equations
67
REFERENCES
Stability,
Oscillations,
and
Chaos
in
Difference
Equations
Frauenthal,
J. C.
(1979).
Introduction
to
Population
Modelling
(UMAP Monograph
Series).
Birkhauser, Boston,
59-73.
Frauenthal,
J. C.
(1983).
Difference
and
differential
equation population growth models.
Chap.
3 in (M.
Braun,
C. S.
Coleman,
and D. A.
Drew, eds.),
Differential
Equation
Models.
Springer-Verlag,
New
York.
Guckenheimer,
J.;
Oster,
G.; and
Ipaktchi,
A.
(1977).
The
dynamics
of
density-dependent
population models.
J.
Math. BioL,
4,
101–147.
Hofstadter,
D.
(1981). Strange attractors: Mathematical patterns delicately poised between
order
and
chaos. Sci. Am., November 1981 vol. 245,
pp.
22-43.
Kloeden, P.E.,
and
Mees, A.I.
(1985).
Chaotic phenomena. Bull. Math. Biol.,
47,
697-738.
Li, T. Y., and
Yorke,
J. A.
(1975). Period three implies chaos. Amer. Math.
Monthly,
82,
985-992.
May,
R. M.
(1975). Biological populations obeying difference equations: Stable points, sta-
ble
cycles,
and
chaos.
J.
Theor. BioL,
51,
511–524.
May,
R. M.
(1976). Simple mathematical models
with
very
complicated dynamics. Nature,
261, 459–467.
May,
R. M., and
Oster,
G.
(1976).
Bifurcations
and
dynamic complexity
in
simple ecological
models.
Am.
Nat., 110,
573-599.
Perelson,
A.
(1980).
Chaos.
In L. A.
Segel,
ed.,
Mathematical
Models
in
Molecular
and
Cel-
lular
Biology. Cambridge University Press, Cambridge.
Rogers,
T. D.
(1981).
Chaos
in
Systems
in
Population Biology,
in R.
Rosen ed., Progress
in
Theoretical
Biology,
6,
91–146.
Academic Press,
New
York.
Physiological
Applications
Glass,
L., and
Mackey,
M. C.
(1978).
Pathological conditions resulting
from
instabilities
in
physiological control systems. Ann.
N. Y.
Acad. Sci., 316,
214-235,
published 1979.
Ikeda,
N.,
Yoshizawa,
S., and
Sato,
T.
(1983). Difference equation model
of
ventricular
parasystole
as an
interaction between cardiac pacemakers based
on the
phase response
curve.
J.
Theor. Biol., 103,
439-465.
Keener,
J. P.
(1981).
Chaotic cardiac dynamics.
Pp.
299–325
in
F.C. Hoppenstaedt,
ed. in
Mathematical
Aspects
of
Physiology.
American Mathematical Society, Providence,
R.I.
Mackey,
M.C.,
and
Glass,
L.
(1977). Oscillation
and
chaos
in
physiological control sys-
tems. Science, 197,
287-289.
Mackey,
M. C., and
Milton,
J.
(1986).
Dynamical
Diseases,
Ann, N.Y. Acad. Sci.,
in
press.
May, R.M.
(1978).
Dynamical
Diseases.
Nature, 272,
673-674.
(See
also
miscellaneous papers
in New
York Academy
of
Sciences (1986).
Perspectives
on
Biological
Dynamics
and
Theoretical
Medicine;
and in
Ann.
N. Y.
Acad. Sci.,
vol. 316.)

68
Discrete
Processes
in
Biology
Miscellaneous
Anderson,
R., and
May,
R.
(1982).
The
logic
of
vaccination.
New
Scientist, November
1982.
Greenwell,
R.
(1984).
The
Ricker salmon model. UMAP Unit
653.
Reprinted
in
UMAP
Journal,
5(3), 337-359.
Hassell,
M. P.
(1975).
Density dependence
in
single-species populations.
J.
Anim. EcoL,
44,
283-295.
Jury,
E. I.
(1971).
The
inners approach
to
some problems
of
system theory.
IEEE
Trans.
Au-
tomatic
Contr., AC–16,
233
–240.
Levine,
S. H.
(1975).
Discrete
time modeling
of
ecosystems with applications
in
environmen-
tal
enrichment. Math. Biosci.,
24,
307-317.
Lewis,
E. R.
(1977). Network
Models
in
Population Biology (Biomath.,
vol.
7).
Springer-
Verlag,
New
York.
Marotta,
F. R.
(1982).
The
dynamics
of a
discrete population model with threshold. Math.
Biosci.,
58,
123–128.
May,
R. M.,
Conway,
G. R.,
Hassell,
M. P., and
Southwood,
T. R. E.
(1974). Time delays,
density
dependence
and
single species oscillations.
J.
Anim. EcoL,
43,
747–770.
Maynard
Smith,
J.
(1974).
Models
in
Ecology. Cambridge University Press, Cambridge,
Eng.
APPENDIX
TO
CHAPTER
2:
TAYLOR
SERIES
PART
1:
FUNCTIONS
OF ONE
VARIABLE
Technical
Matters
In
order
for a
function F(x)
to
have
a
Taylor series
at
some point
XQ,
it
must have derivatives
of
all
orders
at
that point. (The
function
F(x)
- \ x \ at x = 0
does
not
qualify
because
of the
sharp
corner
it
makes
at x = 0.)
A
Taylor
series about
x
0
is an
expression involving powers
of (x —
XQ),
where
XQ
is a
point
at
which
F and all its
derivatives
are
known. Written
in the
form
this
expression
is
called
a
power series
and may be
thought
of as a
polynomial with infinitely
many
terms. Equation
(37)
makes
sense
only
for
values
of x for
which
the
infinite
sum is
some
finite
number
(i.e.,
when
the
series converges). There
are
precise tests
(e.g.,
the
ratio
test)
that determine whether
a
given power series converges.
Suppose T(x)
is a
power
series
that converges whenever
\x —
XQ\
< r (r is
then called
the
radius
of
convergence).
It can be
shown that
provided
the
coefficients
a
n
are of the
following form:

Nonlinear
Difference
Equations
69
where
these
expressions
are
derivatives
of F
evaluated
at the
point
XQ.
A
technical
question
is
whether
the sum
(37) with
the
coefficients
in
(38) actually equals
the
value
of F at
points
x
other than
XQ.
Below
we
assume this
to be the
case.
Practical
Matters
The
Taylor
series
of a
function
of one
variable
can be
written
as
follows:
When
x -
XQ
is a
very small quantity,
the
terms
(x -
xo)
k
for
k > 1 can
usually
be
neglected
(provided
the
derivative coefficients
are not
very
large;
i.e.,
the
function
does
not
make
abrupt
changes).
In
this
case
Figure 2.12 demonstrates
how
this
expression
approximates
the
actual function.
Figure 2,12
By
retaining
the first two
terms
in a
Taylor
series
expansion
for a
function,
the
value
of
the
function
at a
point
x, P
2
=
F(x),
.is
approximated
by the
expression
P
3
=
F.(x)
=
F(XO)
+ Ay =
F(XO)
+
(slope)
Ax.
dF
is the
slope
of
the
tangent line,
*o
The
quantity
-p
and Ax = x — Xo.
Using
these terms
one
arrives
at
an
approximation that
is
accurate
only
when
XQ
and
x
are
close.

70
Discrete
Processes
in
Biology
PART
2:
FUNCTIONS
OF TWO
VARIABLES
Technical
Matters
Consider
the
function
of two
variables F(x,
y)
that
has
partial derivatives
of all
orders with
respect
to x and y at
some point (x
0
,
yo)
such that
Pi =
F(x
Q
, y
0
). Then
the
value
of F at a
neighboring point
P
2
=
F(x,
y) can be
calculated using
a
Taylor
series
expansion
for F,
pro-
vided this expansion converges
to the
value
of the
function.
Since variation
in
both
x and y
must
be
taken into account,
the
series
involves partial derivatives.
It
proves convenient
to
define
the
following quantity:
Using
this notation,
we can now
express
the
Taylor series
of F as
follows:
Practical
Matters
When
(x, y) is
close
to
(xo, yo),
the
function
F can be
approximated
by
retaining
the first two
terms
of a
Taylor
series
expansion,
as
follows:
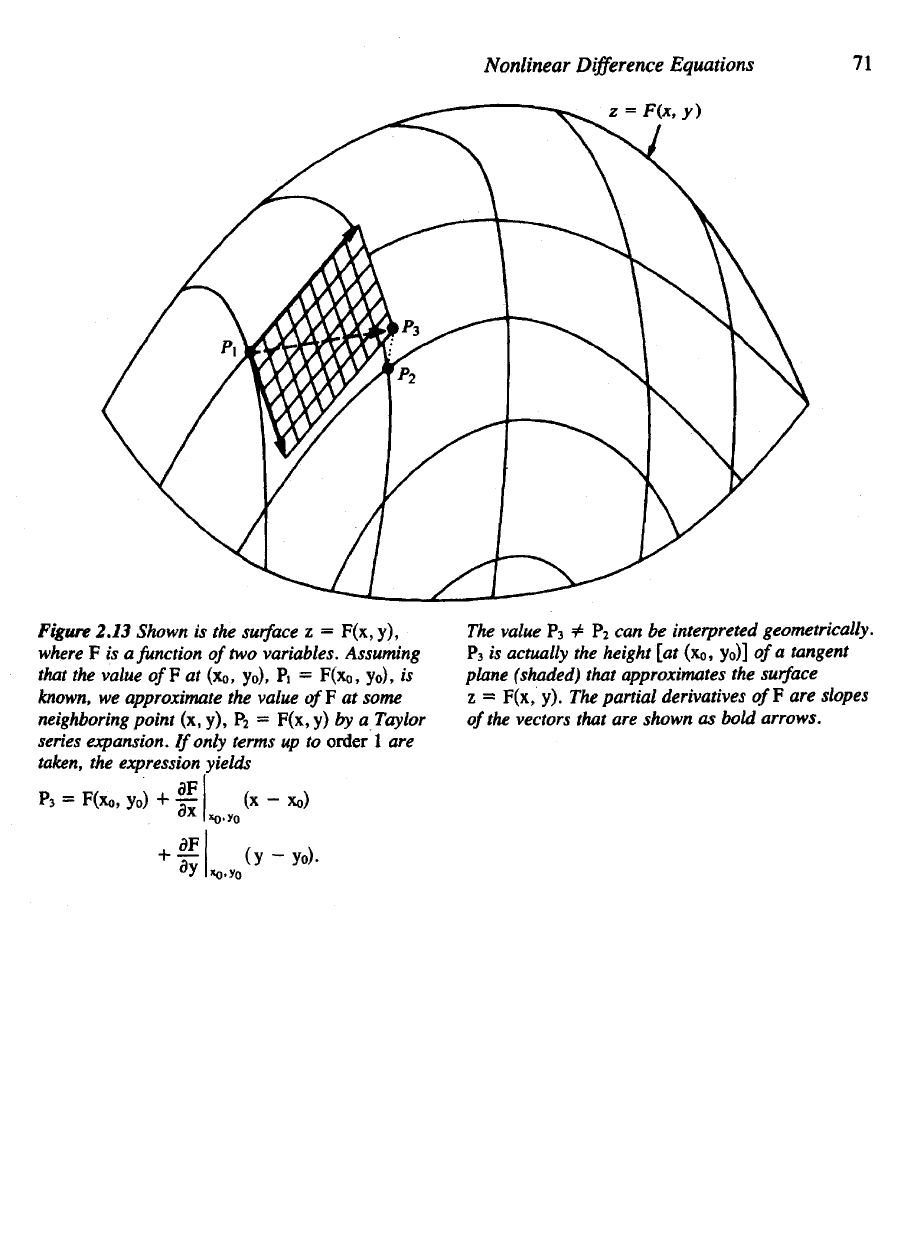
Figure 2.13 illustrates
how
this expression approximates
the
value
of the
function.
The
geo-
metric ideas underlining this expression
are
best understood
by
readers
who
have
had
some
exposure
to
vector calculus.
For
others
it
suffices
to
remark that this
is a
natural extension
of
the
one-variable
case
to a
higher dimension.
By
nth
power
of the
above expression
we
mean
the
following:
In
this shorthand,
the
similarity
to
functions
of one
variable
is
apparent. Note that
the
expres-
sions
A"F are
binomial expansions involving mixed partial derivatives
of F
that
are
evaluated
at
(XQ,
y
0
).
Nonlinear
Difference
Equations
71
Figure 2.13 Shown
is the
surface
z =
F(x,y),
where
F is a
function
of
two
variables. Assuming
that
the
value
of¥ at
(x
0
, yo),
Pi =
F(x
0
, yo),
is
known,
we
approximate
the
value
of
F at
some
neighboring
point
(x, y), P
2
=
F(x,
y) by a
Taylor
series expansion.
If
only terms
up to
order
1 are
taken,
the
expression yields
The
value
P
3
=£ P
2
can be
interpreted geometrically.
P
3
is
actually
the
height
[at
(XQ,
yo)]
of a
tangent
plane
(shaded)
that approximates
the
surface
z
=
F(x,
y). The
partial derivatives
off are
slopes
of
the
vectors that
are
shown
as
bold
arrows.

J
Applications
of
Nonlinear
Difference
Equations
to
Population
Biology
Great
fleas
have
little
fleas
upon
their
backs
to
bite
'em.
And
little
fleas
have
lesser
fleas, and so ad
infinitum.
The
great
fleas
themselves
in
turn
have
greater
fleas to go on,
While
these
again
have
greater
still,
and
greater
still,
and so on.
Anonymous
(1981).
The
brand
x
anthology
of
poetry,
Burnt
Norton edition,
William
Zaranka,
ed.
Apple-wood Books, Cambridge, Mass.
They
hop in
tens
and in
hundreds
they
fly
Thousands
lie
still
while
millions
go by
That
makes
billions
of
bugs
who
jump
and who
crawl
So try as you
will,
you
can't
count
them
all.
Haris
Petie (1975). Billions
of
bugs, Prentice-Hall,
Englewood
Cliffs,
N.J.
Methods
developed
in
Chapter
2
prove
useful
in
addressing
the
population dynamics
of
organisms that have distinct breeding periods
and
life-cycle stages, notably
in-
sects
and
other
arthropods
(the phylum consisting
of
segmented-leg organisms).
Since insects
often
compete
with
humans
for
crops
or
natural resources,
efforts
at
pest management have been
of
fundamental
economic interest.
Recognizing
that chemical sprays
and
toxins
are as
unhealthy
in the
long
run
for
people
as for
pests, recent
efforts
have been directed
at
biological control
of
pest

Applications
of
Nonlinear
Difference
Equations
to
Population
Biology
73
species using other potential competitors, predators,
or
parasites. Folk tradition
has
held that this would lead
to
eradication
of the
undesirable pest.
In
fact,
however,
the
outcomes
of
biological
intervention
are not
always
as
clear-cut
as we
might naively
expect.
We
discover
time and
again that interactions
of a
species
with
the
environ-
ment,
with other members
of its own
species,
or
with
another population
can be po-
tentially
complex
and
bizarre.
To
understand some
of the
outcomes
of
population interactions,
an
examina-
tion
of
fairly elementary mathematical models proves quite illuminating. Here again,
we
make
no
claim
to
describe
the
full
intricacies
of a
given situation. Rather,
the ap-
proach
is to
examine
the
consequences
of
several
simplifying
assumptions.
Often
these assumptions lead
us to
predictions that
are
biologically unrealistic (see
the
Nicholson-Bailey model,
for
example,
as
described
in
Section 3.3).
It is
then
in-
structive
to
consider
how
modifying
the
underlying assumptions tends
to
change
the
predictions.
To
introduce discrete models into population dynamics
we first
consider single-
species populations
in
Section 3.1.
As
indicated
in
Chapter
2,
nonlinear
difference
equations arise rather naturally
in
models
for
populations that have nonoverlapping
generations. Many
of
these models
are
based
on the
observation that
the net
growth
rate
of the
population depends
in
some
way on its
density. These
effects
may
stem
from
competition
of
individuals
for
limited resources
or
from
numerous other envi-
ronmental
considerations
including predation,
disease,
and so
forth.
Single-species
models
are
often
based
on
empirical
formulae
rather
than
on
detailed interactions
in
the
population.
We
examine several
of
these
in
Section 3.1.
In
many ecological settings
one finds
that
two or
more species
are
intimately
related
in
their influence
on
each other.
A
classic example, that
of the
host-parasitoid
system,
is
outlined
in
Sections
3.2
through 3.4. Here
one
species
(the parasitoid)
can
reproduce only
in the
presence
and at the
expense
of the
other (its host).
We
observe
that
under
the
simplest reasonable assumptions,
a
model
for
such systems (the
Nicholson-Bailey model) predicts growing population oscillations
in the two
species.
Section
3.4
summarizes
a
number
of
potentially stabilizing
influences.
Models
described
in
Sections
3.1
through
3.4
proceed largely
from
detailed
choices
for
functions that represent growth rates, fraction
of
hosts parasitized,
or
survivorships.
In a
model
for
plant-herbivore interactions (Section 3.5)
we
depart
somewhat
from
this traditional approach.
We
observe that certain logical deductions
about
population behavior
can be
made even
when
only broad features
of the
system
are
known.
For
would-be modelers this approach
is an
instructive
one and
reappears
in
later material.
Sections
3.5 and 3.3 as
well
as 3.1
contain several explicit exam-
ples
of how to
apply
the
stability criteria derived
in
Chapter
2. As
such, these exam-
ples
may
enhance your appreciation
of the
techniques previously developed.
The
concluding section
of
this chapter contains some introductory material
on
population genetics. This topic provides
an
excellent example
of yet
another realm
in
which discrete difference equations
are
important.
Note
to the
instructor:
For
rapid coverage
of
this chapter, include only Sec-
tions
3.1
through
3.3 and
3.6, leaving Sections
3.4 and 3.5 for
further
independent
study
by
more advanced students.

74
Discrete Processes
in
Biology
3.1
DENSITY DEPENDENCE
IN
SINGLE-SPECIES POPULATIONS
1
An
assumption that growth
rate,
reproductive rate,
or
survivorship depends
on the
density
of the
population leads
us to
consider models
of the
following
form:
Next,
we let
where
f(N
t
)
is
some (nonlinear)
function
of the
population density.
Quite
often
single-species populations
(of
insects,
for
example)
are
described
by
such equations,
where/is
a
function
that
is fit to
data obtained
by
following
suc-
cessive
generations
of the
population. Here
we
consider several models
of
this type
and
demonstrate their properties.
1.
A
model
by
Varley, Gradwell,
and
Hassell (1973) consists
of the
single equation
Here
A is the
reproductive rate, assumed
to be
greater than
1, and I/a N
t
b
is the
fraction
of the
population that survives
from
infancy
to
reproductive adulthood.
The
equation
is
thus best understood
in the
form
where
a, b, A > 0.
Since
the
fraction
of
survivors
can at
most equal
but not
exceed
1,
we find
that
the
population must exceed
a
certain
size,
N
t
> N
c
for
this model
to
be
biologically reasonable (see problem
1).
Populations
satisfying
equation
(3) can be
maintained
at
steady density levels.
To
observe this
we
look
for the
steady-state solutions
to (3) by
setting
Substituting
into
(3) we find
that
Cancelling
the
common factor
N and
rearranging terms gives
us
1.
This section contains material compiled
by
Laurie Roba.

Applications
of
Nonlinear
Difference
Equations
to
Population
Biology
75
and
proceed
to
test
for the
stability
of N. We find
that perturbations
8, from
this
steady state must
satisfy
It is
clear
that
b — 0 is a
situation
in
which survivorship
is not
density-dependent;
that
is, the
population grows
at the
rate A/a. Thus
the
lower bound
for the
stabiliz-
ing
values
of b
makes sense.
It is at first
less clear
from
an
intuitive point
of
view
why
values
of b
greater than
2 are not
consistent with stability;
it
appears that den-
sity
dependence that
is too
strong
is
destabilizing
due to the
potential
for
boom-and-
bust
cycles.
2. A
second model cited
in the
literature (for example, May, 1975) consists
of the
equation
Since
N =
f(N),
recall
that this simplifies
to
But
Thus
stability
of N
hinges
on
whether
the
quantity
1 - b is of
magnitude smaller
than
1;
that
is, N
will
be
stable provided that
or
where
r, K are
positive constants.
The
quantity
A = exp r(l
—
N
t
/K) could
be
con-
sidered
the
density-dependent reproductive rate
of the
population. Again,
by
carry-
ing
out
stability analysis
we
observe that
is the
nontrivial steady state.
To
analyze
its
stability properties
we
remark that
for
we
have
Evaluated
at N = K,
(10) leads
to
