Дубровский В.Г. Теоретические основы технологии полупроводниковых наноструктур
Подождите немного. Документ загружается.

G+=Φ
ζ
Здесь идеальное пересыщение как функция времени
(2.89)
имеет вид
⎨
>
=Φ
0
)(
t
t
(2.90)
есть время, за которое концентрация адатомов достигает
n
eq
при постоянном потоке материала на поверхность J в
изменения полного
(t)=Jt при t<t
0
и n
tot
=n
max
=Jt
0
при t>t
0
. Величина
Φ
0
есть
адатомов, достигаемое в момент остановки роста.
островков в им с ос
енному в п. II.2. Именно, будем рассматривать
нуклеации, число атомов в островках и другие
*
(t) есть максимально представительный размер островков, зародившихся при
формулой (1.47). Очевидно, точка максимума
соответствует x 0. В
распределения островков по размерам, выраженная в единицах равновесной концентрации
адатомов на поверхности n
eq
, есть
)())((),( xfxftf ≡=
⎩
⎧
Φ≡−
≤−
∞
∞
00
0
,1/
,1/
ttt
tttt
Характерное время t
∞
=n
eq
/J
своего равновесного значения
отсутствие десорбции. Это время задает характерный масштаб
количества материала на поверхности. Очевидно,
Φ
(t)=n
tot
(t)/n
eq
-1, где полная
поверхностная концентрация атомов (в составе островков и двумерного пара адатомов) в
рассматриваемом случае есть n
tot
максимальное идеальное пересыщение
Для исследования процесса нуклеации реж е тановкой роста
воспользуемся методом работ [24,60], который технически несколько отличен, но идейно
полностью эквивалентен методу, излож
пересыщение адатомов, скорость
физические характеристики
процесса нуклеации как функции переменной x(
ρ
,t)=z(t)-
ρ
.
Здесь z(t)
≡ρ
максимальном пересыщении, определяемый
пересыщения в терминах переменной x = частности, функция
s
ζ
ρ
(2.91)
где f
s
(ζ)=I(ζ)
τ
D
/
ς
т
eq
– безразмерная стационарная функция распределения, определяемая
из (2.6)
139

⎥⎢
−+= exp)1(ln)(
ζζ
f
(2.92)
е
∫
⎦
⎤
⎣
⎡
+
+
)1ln(
)1(1
2/1
ζζ
ζ
θπ
a
eq
s
В терминах безразмерной функции распределения островков обще число атомов в
островках G имеет вид
∞−
−= xfxzdxzG )()()(
2
ее вблизи точки максимума
z
(2.93)
где учтено, что число атомов в островке размера
ρ
равно
ρ
2
=(z-x)
2
.
Действуя аналогично п. II.2, воспользуемся экспоненциальной зависимостью
функции распределения (2.92) от пересыщения и представим
пересыщения ζ
*
≈Φ
*
в виде (2.8)
()
⎥⎢
−Φ−Φ=
∗∗
)(exp)()( xfxf
ζ
(2.94)
>ΓΦ
+Φ
=Φ
00**
*
,)/(
(
)(
zxz
x
⎦
⎤
⎣
⎡
Φ
Γ
∗
s
Параметр
Γ
>>1 здесь имеет тот же вид, что и в (2.9). Идеальное пересыщение
Φ
заменим
линейной аппроксимацией вблизи x=0
⎩
⎨
⎧
+Φ
≤ΓΦ
0*
,)/ zxcx
(2.95)
Параметр
eq
D
eq
x
V
d
τ
**
0
Γ
ΓΦΓ
=
(2.96)
с поверхности. Кинетический контрольный параметр Q в (2.96) совпадает с (2.19).
0
Q
dx
c
θθ
23/12
*
Φ
=
Φ
=
Φ
=
получается из формулы (2.32) при
ε→
0, или
τ
A
→∞
, поскольку мы пренебрегли десорбцией
Величина z в (2.95) определяется отношением максимального идеального пересыщения в
момент остановки роста
Φ
0
и максимального пересыщения адатомов
Φ
*
:
⎟
⎟
⎠
⎜
⎜
⎝
−
Φ
= 1
*
0
c
z
(2.97)
⎞
⎛
Φ
Γ
0
140

Как было показано в п. II.2, в режиме без остановки роста максимум пересыщения
достигается за счет того, что поступление атомов на поверхность из газообразной среды
уравно
м значении пересыщения
Φ
с
, которое при данных условиях роста и параметрах
вешивается их потреблением растущеми островками. Это наблюдается при
критическо
системы определяется формулой (2.18). В режиме без остановки роста критическое
пересыщение одновременно является и максимальным пересыщением, то есть
Φ
с
=
Φ
*
.
Для исследования зависимости структурных параметров растущего слоя от температуры
поверхности учтем, что для конденсированных сред межфазовая энергия границы
двумерного островка
ε
может быть представлена в виде [213]
sTkh
B
∆−∆=
ε
(2.98)
Здесь
∆
h и
∆
s – изменения энтальпии и энтропии системы при образовании границы
е
островка, отнесенные к единицы длины этой границы, которые в некотором интервале
температур можно приближенно считать не зависящими от T. Тогда из выражения (1.26)
для эн ргетической константы a получаем
2
4
1
⎞
⎛
=
T
a
A
A В
ы
⎟
⎠
⎜
⎝
− B
T
(2.99)
где T
≡
4
σ
1/2
∆
h/k – параметр размерности температуры и B
≡
4
σ
1/2
∆
s – безразмерная
константа. Используя (2.99) и формулу (2.19) для Q, в ражение (2.18) для критического
пересыщения можно представить в виде
()
1
/)3/10(/ln12
exp),(
2
−
⎟
⎟
⎠
⎜
⎜
⎝
+−
=Φ
TTTV
VT
A
c
ν
(2.100)
D D c
)/(
1
⎞
⎛
− BTT
cDD
где T
D
≡
E
D
/k
B
– характерная диффузионная температура и Т
с
– критическая температура
фазового перехода. Из (2.100) следует, что критическое пересыщение убывает при
увеличении температуры поверхности и несколько медленее возрастает с увеличением
потока вещества на поверхность. Поскольку всегда ln(
ν
/V)>>(T +10T /3)/T, главная
температурная зависимость критического пересыщения содержит лишь энергетические
141
параметры T
A
и B, а значит, величина критического пересыщения определяется, в
основном, термодинамикой системы.
Очевидно, в
ситуации:
режиме с остановкой роста возможны две принципиально различные
1)
Закритические количество осажденного материала n
max
>n
c
=n
eq
(
Φ
c
+1). Максимальное
остановки роста больше ,
тогда
Φ
0
>
Φ
c
,
Φ
∗
=
Φ
c
<
Φ
0
и z
0
>0. Максимум поверхностной концентрации адатомов
достигается за счет кинетического баланса процессов адсорбции и поглощения адатомов
островков в присутствии потока вещества на поверхность, для которого справедливы
идеальное пересыщение в момент критического пересыщения
растущеми островками. При достаточно больших z
0
этот случай соответствует нуклеации
результаты п. II.2.
2) Докритическое количество осажденного материала n <n =n (
Φ
+1).. Максим
max c eq c
остановки роста меньше критического пересыщения,
ого пересыщения (2.95)
откуда выражаем разность
Φ
∗
-ζ(x) через G(x). Получившееся
островков. Далее используем эту формулу в (2.93), что, как и ранее, дает замкнутое
интегральное уравнение для числа атомов в островках G(x). Это уравнение решается
итерациями, причем мы ограничиваемся точностью первой итерации, которая
соответствует подстановке G=0 в подинтегральное выражение
в правой части (2.93).
Получившийся интеграл разбивается на два, с областями интегрирования по x при x<z
и
при x>z
. Оба интеграла легко вычисляются аналитически. Полученное выражение для
G(x) подставляется в (2.94), откуда получаем функцию распределения по размерам в
альное
идеальное пересыщение в момент
тогда
Φ
0
<
Φ
c
,
Φ
∗
=
Φ
0
и z
0
=0. Максимум поверхностной концентрации адатомов
достигается просто в результате остановки роста.
Общее выражение для поверхностной плотности адатомов в режиме с остановкой
роста получается следующим образом [212]. Формула для идеальн
подставляется в (2.89),
выражение подставляем в формулу (2.94) для функции распределения по размерам
0
0
142

терминах переменной x. Поверхностная плотность островков по окончании стадии
зарождения N
isl
определяется инте рированием функции распределения f(x) по x
∫
eqisl
(2.101)
Окончат
г
∞
∞−
= )(xdxfnN
ельный результат для N
isl
имеет вид
(
)
)(1 fGeKNN
f
isl
+−=
−
где
(2.102)
⎧
Φ≤Φ+Φ+Φ+Φ+ΦΦΦ
c0
),1ln()1/()1ln()1()/(
()
⎩
⎨
Φ>Φ
=
cccc
K
000
2
0
,1
(2.103)
[
]
⎧
Φ≤ΦΦ−Φ−+Φ+ΦΦΦ+Φ+Φ
ccc
c
FF
00
0
422/9
,)()(exp)]1/()1[()/()]1ln(/)1[ln(
⎩
⎨
Φ>Φ−ΦΦΓ
=
cccc
f
0000
)],1/(exp[
(2.104)
∫
∑
⎥
⎢
−=
exp)(
i
fdffG
µ
∞
⎤
⎡
3
i
µ
=
⎦
⎣
0
0
!
i
(2.105)
Здесь F(
Φ
)=a/ln(1+
Φ
) есть активационный барьер нуклеации и
Γ
c
≡Γ
(
Φ
c
). Максимальная
поверхностная плотность островков, наблюдаемая в закритической области количества
осажденного материала, совпадает с выражением (2.24) при
ε→
0
3
2
3
)(
2
eq
D
c
c
Vt
θ
σ
Φ
Γ
Наиболее представительный латеральный размер островков L в режиме с
остановкой роста не
N
=
(2.106)
возрастает неограниченно, как в случае постоянного осаждения, а
квазистационарному значению L
R
, соответствующему
размерам. В конце данной стадии концентрация
равновесному значению, а весь остальной материал
островках
охлаждается, в режиме с остановкой роста обязательно будет наблюдаться стадия
стремиться к вполне определенному
окончанию стадии релаксации по
адатомов стремиться к своему
оказывается распределенным в . В дальнейшем, если поверхность не
143

Оствальдовского созревания [61]. Однако эта стадия требует лительной кспозиции
поверхности и происходит на временах, много больших, чем характерное время
релаксации островков по размерам. Квазистационарный размер островков L
д э
)
R
легко
оценить из уравнения баланса вещества на поверхности при ζ
→
0:
Φ
0
=G
≈
(N
isl
/n
eq
(L
R
/l
0
) ,
откуда
2
2/12/1
)(
⎞⎛
−
⎞⎛
nnn
max
eqeq
R
, медленнее,
сажденного материала. Квазистационарный размер L
R
есть максимально
Выражения (2.102)-(2.107) позволяют описать два предельных механизма
0
⎟
⎟
⎠
⎜
⎜
⎝
=
⎟
⎟
⎠
⎜
⎜
⎝
Φ=
islisl
R
NN
L
σσ
(2.107)
Разумеется, реально наблюдаемый размер островков L(t) на стадии релаксации по
размерам может быть меньшим L
причем островки растут тем чем меньше
количество о
достижимый размер островков при данном количестве материала на поверхности.
формирования островков в режимах с остановкой роста [212]:
1)
Кинетический механизм, который наблюдается при существенно закритическом
количестве осажденного материала. Этот случай соответствует
f>>1 в формуле (2.102).
Тогда K=1, G(f)
→
0 и N
isl
→
N, то есть ков такая же, как и в режим плотность остров е с
постоянным потоком материала на поверхность. При этом, как следует из (2.106) и (2.107)
роста (диффузионной температурой T
D
и скоростью осаждения материала V) и не
нуклеации (T
A
и B):
п определяются кинетикой ри
Φ
c
~1, структурные характеристики ансамбля островков
содержат термодинамических параметров, связанных с активационным барьером
⎥
⎦
⎤
⎢
⎣
⎡
+
∝=
T
TT
VNN
isl
62
exp
1
σ
(2.108)
cD
2
⎟
⎠
⎜
⎝
−∝
TV
L
cD
R
exp
2/1
2/1
σ
(2.109)
⎞⎛
+Φ TT
3
0
144

При закритическом количестве осажденного материала плотность островков
увеличивается при увеличении потока, меньшается при увеличении температуры и не
зависит от количества осажденного материала. Характерный размер островков по
окончании стадии релаксации по размерам уменьшается при увеличении
у
потока,
велич
ко в
у ивается при увеличении температуры и степенным образом увеличивается при
увеличении личест а осажденного материала.
2)
Термодинамический механизм, который наблюдается при существенно докритическом
количестве осажденного материала. Этот случай соответствует f<<1 в формуле (2.102).
Тогда 1-exp(-f)
≈
f, а асимптотика функции G(f) в (2.105) при малых f определяется
выражением
∫
∞
⎟
⎜
Γ=
⎟
⎜
−=
exp)(
ffdffG
µ
(2.110)
к
и асимптотического соотношения
⎠
⎞
⎝
⎛
⎟
⎠
⎞
⎜
⎝
⎛
0
3/2
3/2
3/13
3
1
3
2
6
µ
где
Γ
(x) – гамма-функция. Как следует из (2.104), при существенно докритических
оличествах осажденного материала по порядку величины функция f~exp[F(
Φ
c
)-F(
Φ
0
)].
Поэтому поверхностная плотность островков N
isl
~ exp[F(
Φ
c
)-F(
Φ
0
)]N, что с учетом (2.106)
[]
1~)(exp
D
F Φ
, следующего из (2.17), дает
)(
5
3
c
eq
Vt
θ
⎥
⎤
⎢
−
−−=
Φ−∝ exp)(exp
FN
(2.111)
⎦
⎣
⎡
+Φ
⎥
⎦
⎤
⎢
⎣
⎡
)1ln(6
)/(
3
2
1
3
2
0
2
0
3/1
BTT
T
T
A
c
eq
isl
σσ
θ
⎥⎢
+=
⎥
⎢
∝ exp
exp
L
R
σ
(2.112)
и
экспоненциально увеличивается с
величением количества осажденного материала. Размер островков по окончании стадии
⎦
⎤
⎣
⎡
+Φ
−
⎦
⎤
⎣
⎡
Φ
)1ln(12
)(
33
)(
0
2
2/1
0
6/1
2/1
BTT
T
TF
A
c
eq
θ
σ
Полученные выражения для плотности и размера островков в рассматриваемом случае
имеют чисто термодинамическую природу, поскольку они содержат только равновесные
параметры T
c
, T
A
и B и вообще не зависят от кинетик роста. Плотность островков
увеличивается при увеличении температуры и
у
145
релаксации по размерам уменьшается при увеличении температуры и при ув
количества осажденного материала. Структурные характеристики докритических
ансамблей островков не зависят от скорости осаждения материала V, поскольку
длительной стадии нуклеации неважно, с какой скоростью материал был осажден.
Таким образом, при увеличении количества осажденного материала n
max
в режиме
остановкой роста до критической концентрации n
c
происходит переход
термодинамического к кинетическому механизму формирования островков. Проведенное
рассмотрение позволяет представить поверхностную плотность N и квазистационарный
островков L
R
в виде функций от трех управляющих параметров ростового
процесса: температуры T, скорости осаждения материала V (или потока J) и количества
осажденного материала n
max
(или идеального пересыщения в момент остановки роста
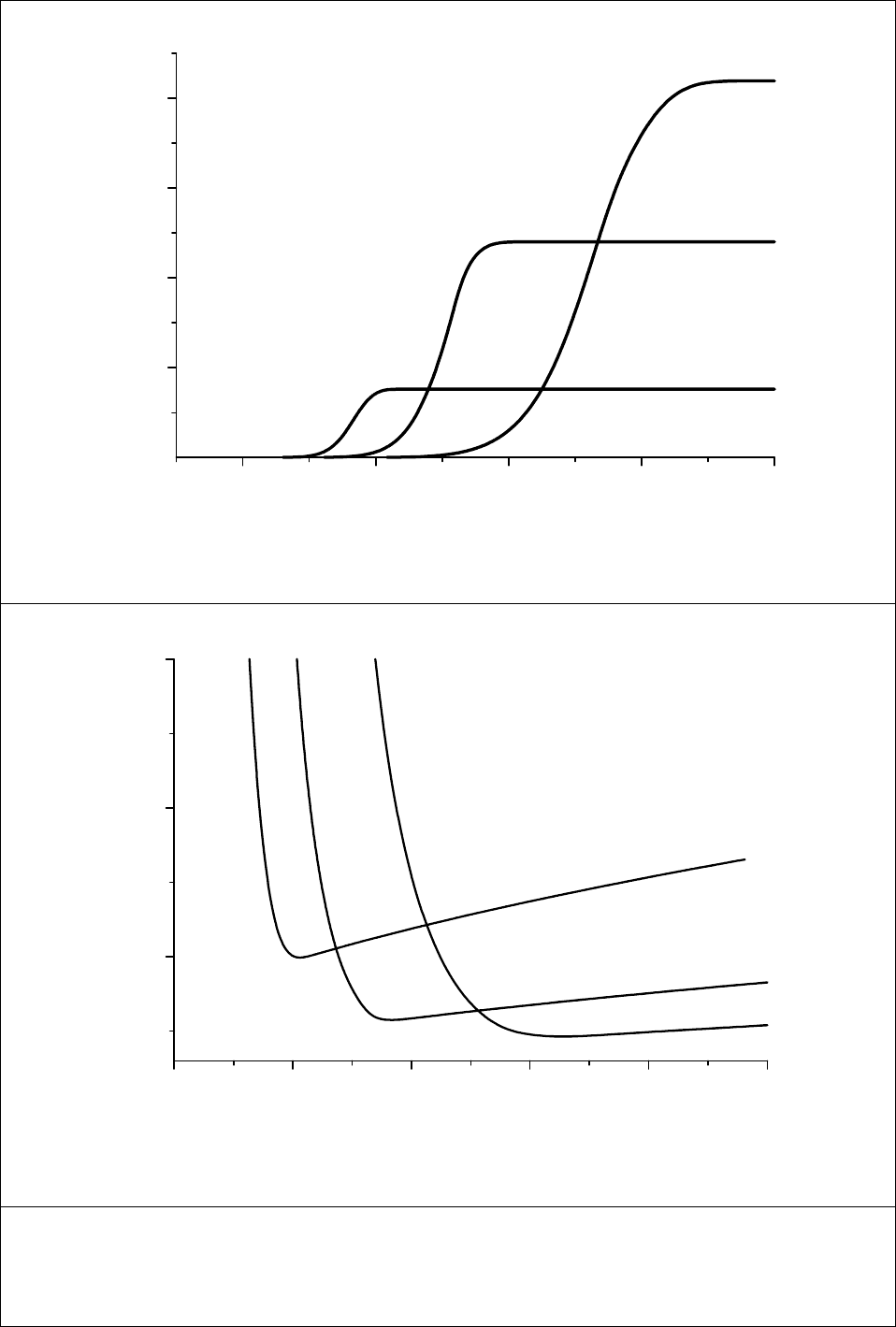
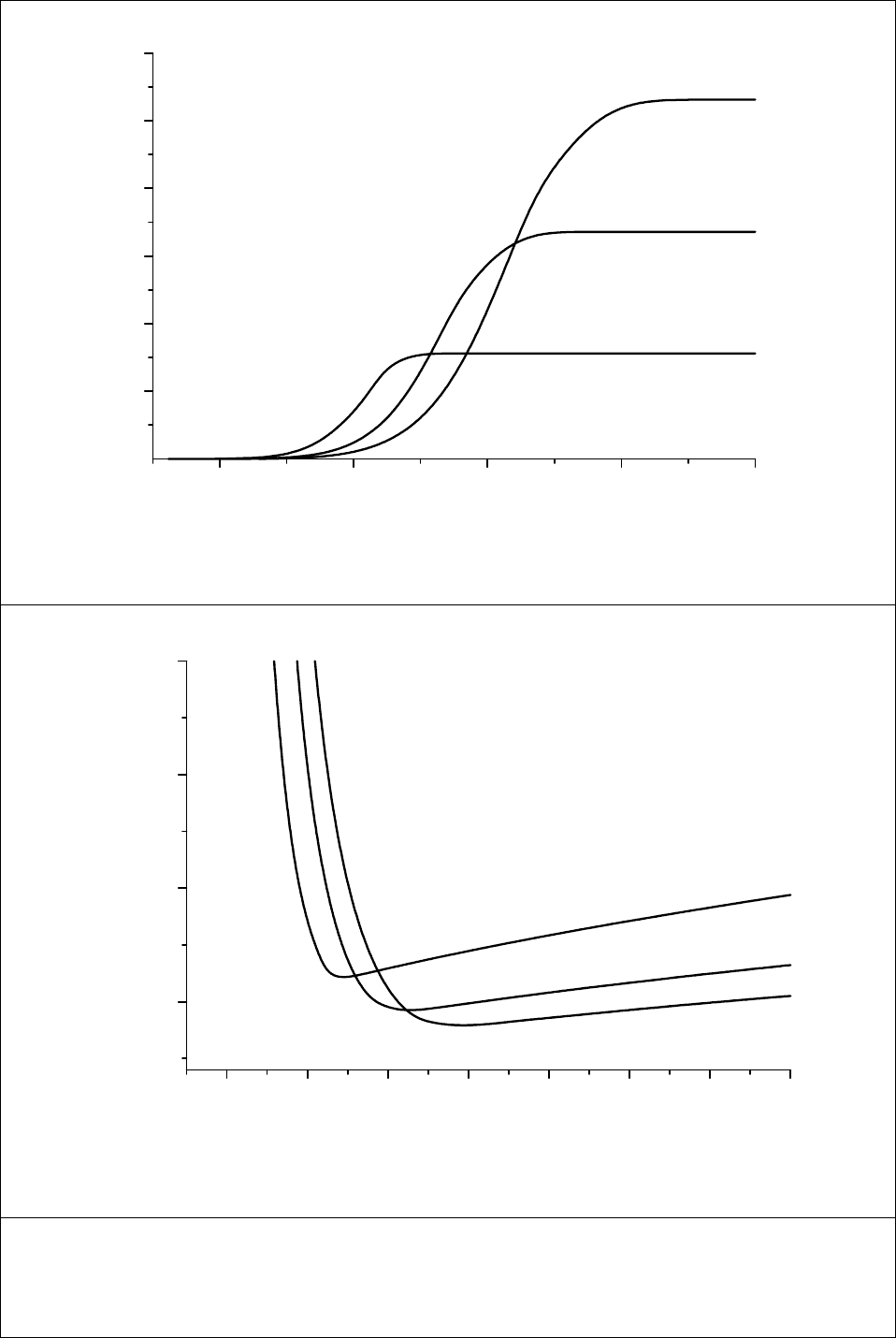
таких зависимостей представлен на Рис. 37 и 38. Плотность и квазистационарный
еличении
при
с
от
размер
Φ
0
).
Пример
Φ
при
по
T
A
от
Φ
так
что
при
повыш в
докритической
размер островков представлены в виде функций максимального идеального пересыщения
0
при фиксированном потоке и различных температурах (Рис. 37) и, наоборот,
фиксированной температуре и различных потоках (Рис.38). Вычисления проводились
формулам (2.102)-(2.107) для следующих значений параметров:
σ
1/2
=0.4 nm, T
c
=2200 K,
=4200 K, B=1, T
D
=10500 K (E
D
≈0.9 eV) и
ν
D
=10
12
s
-1
. Из рисунков видно, что вблизи
критического значения идеального пересыщения
Φ
с
происходит переход
термодинамически к кинетически контролируемому режиму нуклеации островков. Вблизи
с
зависимости N и L
R
от потока J при фиксированной температуре T расщепляются,
в закритической области
Φ
>
Φ
с
плотность островков при увеличении J становиться
больше, а размер L
R
– меньше. Зависимости N и L
R
от температуры T при фиксированном
потоке J вблизи
Φ
с
опрокидываются. В закритической области плотность островков
ении температуры уменьшается, а их размер увеличивается, тогда как
области ситуация обратная.
146
0.2 0.4 0.6 0.8 1.0
4.0x10
7
8.0x10
7
1.2x10
8
1.6x10
8
T=650K
T=625K
T=600K
Island density N
isl
[cm
-2
]
Maximum ideal supersaturation Φ
0
0.2 0.4 0.6 0.8 1.0 1.2
100
200
300
T=600K
T=625K
T=650K
Lateral size L
R
[lattice spacings]
Maximum ideal supersaturation Φ
0
Рис.37. Зависимости поверхностной плотности двумерных островков N
isl
и их
максимального размера по окончании стадии релаксации по размерам L
R
от
Φ
0
при трех
зличных темперурах поверхности и фиксированном потоке J=2x10ра
-1
.
10
см
-2
сек
147
0.4 0.6 0.8 1.0 1.2
7
1.0x10
8
1.5x10
8
8
2.5x10
8
3.0x10
8
5.0x10
2.0x10
J=3.3x10
10
cm
-2
s
-1
J=2x10 cm s
J=0.8x10
10
cm
-2
s
-1
N
l
[cm
-2
]
Maximum ideal supersaturation Φ
0
10 -2 -1
Island density
is
0.4 0.6 0.8 1.0 1.2 1.4 1.6 1.8
50
100
150
200
J=3.3x10
10
cm
-2
s
-1
J=2x10 cm s
J=0.8x10
10
cm
-2
s
-1
Average size L
Maximum ideal supersaturation Φ
0
10 -2 -1
R
[lattice spacings]
Рис.37. Зависимости поверхностной плотности двумерных островков N
isl
и их
максимального размера по окончании стадии релаксации по размерам L
R
от
Φ
0
при трех
различных потоках и фиксированной температуре поверхности T=600 K.
148
