Duan C.G., Karelin V.Y. Abrasive Erosion and Corrosion of Hydraulic machinery
Подождите немного. Документ загружается.


104 Abrasive Erosion and Corrosion of Hydraulic Machinery
And F
Mi
is the Magnus force. The drag term expressed in Equation (3.15)
also can include effects of the added mass force and the Basset force, which is
discussed in the section 3.2.4 for the unsteady particle motion.
For the two-phase flow at the dilute concentration condition the
momentum equations for of liquid phase are in the following form:
Ot OX, OX
i
OX
i
k X
rk
(3.17)
And momentum equations for particulate phases are as follows:
*
+
J-0W«) = P
k
Si
+
—(Mi -««)
+ *<A +
F
mi
(3.18)
In Equation (3.18) it is assumed that pressure and viscosity stresses are
zero,
that is, \.ft)
=
0 , \
T
k,ji)
=
®, for dilute concentration particulate
phase.
The energy equation and the component equation also can be obtained in
similar forms.
Basic Equations by Using an Expression of Particle Number n^ in a Unit
Volume.
By using Equation (3.11), Equations (3.10) and (3.18) have the following
form
a &j
klg;
(3.19)
a dx
j
r
rk
m
k
(3.20)

Analysis and Numerical Simulation of Liquid-Solid Two-Phase Flow
105
Basic Conservative Reynolds Averaged Equations for Turbulent Two-Phase
Flow
By using Reynolds averaging method to average basic equations of laminar
two phase flow, i.e., equation (3.14) to equation (3.20), the basic equations of
turbulent dilute liquid-particulate two-phase flow can be obtained as follows.
(1) Continue equation for liquid phase
(2) Continue equation for
&th
particulate phase
dp d
P
+^-(P^J =
«+S
p
(3.22)
dt dx
i
where the averaging note ' ' for every variable has been removed off for
simplicity. And the superscript ''' represents fluctuate value of turbulence
i.i _>..i „_/ i
pUj,
p
k
u
kj
,n
k
m
k
and so on are correlative terms in turbulence. Equation
(3.22) is expressed in the form of particle number in equation (3.23).
dn
k
8 i \ d
+ -r—
(
n
k
u
ki
)=-^—KK
+s
*
(3
-
23
>
dt dx. dx
J
(3) Momentum equations for liquid phase
d , , d . , DP d
—
if",■)
+ -—
(pUjU,)
= —— + —-
dt dXj dx
i
dXj
duj du,. 2 <2u,
dx, dx. 3 dx,
^
p
p
{
^ v o
d
^
pu
i
Ui
)
NP
m
p
i~r~r ~T~T\
T
rp <*/
T
rp
-(M
l
Y.
n
P
™P
+
H
n
P
u
'
rh
'p
+
H™P
u
'> K +Z
M
>X)
(3.24)

106 Abrasive Erosion and Corrosion of Hydraulic Machinery
(4) Momentum equations for particle phase:
d(nu.) d(nu.u.) n„ F
n
. fl
dt dx
j
**' T^ '
p,J
m
p
cT
p p,J
+ n
p
-(u
i
-u
pi
)
m„
d
m
p
dXj
(nu'.u'. +u.n'u' +u.n'u' +n'u'u')
\ p pj pi pj p pi pi p pj p pj pi->
(n'u'-n'u' ) i ——- ——
+ " ' " "' +—<M
t
ri
p
m' +n
u\rti
+m n u\ + rim'u\
rp
m,
. .%'m' —n u' m'
pi p p p pi p
-u n m —n urn —m n u —n m u )
■*„,»«„"«„
»»„■»„,«»»„ „,
p
,i
p
^
pl
"
p
'"p"
pl/
r
(3.25)
where, the Coriolis force is in the following relation:
F=-YF
..
Cl / i p,Cl
And
T■
is the particle dynamic response
time,
which can be expressed in
the following Wallis-Kiliachko drag formula,
T
rp =
d pp„ f * ^
-^
1
+ /JI/6
18//
I j
(3.1<fl
e
<1000)
and R
e
is the relative Reynolds number:
R
e
=d\u-u
p
Iv
(5) Energy equations of liquid phase

Analysis
and Numerical Simulation
of
Liquid-Solid Two-Phase
Flow
107
-cjJ^\^c
p
Y
j
n
k
TW
k
-c^m^-^{c
p
yr')
d
ipc
p
u'
j
T'+u
J
c
p
pT+c
p
Tu'
J
p'
+
c
p
p'u'
j
T
dX
i (3.26)
where Q
k
is
the heat transfer caused by convection between liquid phase and
particulate phases for every particle.
Q
k
=mi
k
N
u
X(T
k
-T)
ln
(
l
+
B
l
B
where Qh
is the
heat reaction
on
particle surface. And
Q
s
is the
heat
of a
particle produced in chemical reaction.
(6) Energy equation of &th particulate phase
^f^-fr-.v.rj-"-®-a
-a,y
t
V-«W
j
(c
k
KT\)--~(n
k
cjy
kj
.+c
k
u
kJ
MlT;
+
cJ
k
n'
k
u'
kj
-+c
k
n'
k
T
k
V
kJ
)
dt^"
"
K
' ac
}
+ (c
p
Tri
k
m'
k
+c
p
n
k
TW
k
+
c
p
m
k
ri
k
T'+ c
p
m'
k
T'ri
k
+c
k
Tn'
k
m
k
CkKm'XX
c
p
T
k
m'
k
n
k
+c
k
T
k
n'
k
m'
k
^
(3 27)
(7) The turbulent Reynolds stresses equations for liquid phase
g
ff g r
—
(pu'
i
u'
J
+
—
(pu
k
uy
j
)
=
-—-\pu'
k
u\u'. +p'u'.S.
k
+p'u'
i
S
J
dt
ck
k
dx
k
+
M
Jk
—(i#;«)-P(«X
—
L
+u'
j
u
,
k
-^)-2p(—^-—^,
ox
k
dx
k
dx
k
ox
k
cx
k

108
Abrasive Erosion and Corrosion of Hydraulic Machinery
du'
du' ^n„m„
+ P'(—
L
)
+
T
-
J
—^KV*
+ « - 2w>') + 2u'
l
u'
+
S
(3.28)
(8) The turbulent Reynolds stresses equations for particle phase
0 g du .
—(n„u'.u')-\
(nu.u'.u'.)
=
-(n„u'.u'
+
u.n'u'.)——
<-y
v
P P> PJ' fl \ p pk pi pj / \ p pk pj pk p pj
■>
o
du . du . du,
(n u',u'+u
k
n'u' )——
—
n'u\u'.—-—n'u'.u'
V p pk pi pk p pi) o P pk pj ~ p pk pi ~
d
(n u',u' u' +u .n'u'.u'.
+
n' u',u' u' )
V>
p
"
pk
"
p
,"
p
j '
P
k p pi pj p pk"pi"pjS
m
p
+
m
p
r,
P rp
~ k (
U
'KJ
+
u
'i
u
pi
-
2U
'PKJ
) +
u
i KKJ
m
p
T
rp
du„,
du. d
-n'jt'n,—--n'u',—JL-SL. (n'u'.u'.) (3.29)
p PJ
dt
p p
' dt dt
p
"'
PJ
(9) The equations of correlation terms between the particle number
density fluctuation and the velocity
fluctuation,
n
'
s
v
'
gi
' , for particle phase
@ ff
—("„«X,')
+ — (
n
p
u
pk
n
'p
u
pi) = -(
n
p
n
p
u
pk+Upk
n
'prip
+
riprip
u
'pk)
du . dn
x
-^-(
2u
pi
n
>P*
+n
p
u
>'
P
i +Upk"'p
u
'
P
i
+n
»'
P
i
+n
»'pj)^-
— du, d
-(2nn'u'
t
+2u„
i
n'ri
+
2n'n'u')——-—(n'riu'.u')
\ p p pt pi p p p p pi
>
- o, _ V p p pk pi J
dx
k
dx
k

Analysis and Numerical Simulation of Liquid-Solid Two-Phase Flow
109
+
m
p
T
rp
-k»;(«.-«
l
.)-'',W)-«;»;«;]-«^;'';^-
d d
dn
r
aKK»',)-aV,»W-»>.
m
du'
pt -,. "P"P"P>
dx,
d
d d
v
?i
^(»X)-s^K«>;j-"M^(»>;%)
du'
-nnu.
p p
"' dx
Pk
-IttM^n'
du' du'
P
pi
P
dx,
vk
-In
v
n'u' —*-
p p
"' dx,
(3.30)
(10) The equation of correlation term of the particle number density
-'2
fluctuation, n , for particle phase
— («X
2
) + — (nu.n'
2
) = ——{nn'
2
u')-(2nn'
2
— u')
dt
K p p)
dx
k
p pk p)
dx
k
pppkJ
K p p
dx
k
pk)
-2n n'
2
u. -Inn'u',—
p
--2n
2
n' u
p p
dx
k
pk p p pk
dx
k
p p
dx
k
pk
—^
du
P
k 1 &*
-n — u
p
dx
k
3
pK
dx
k
>2
p
n'
2
Sn\u'
pk
i g —
dx
k
3 dt
K
3
)
(3.31)
(11) The turbulent energy dispassion equation for liquid phase
, x
d
t
^ ^\ , du'
n
du) du\ du
t
(pe) + (pu
i
£) = -2ju '—.u' —'—2 ft—-—
dt dXj dx
J
dx
k
dXj dx
k
dx
k
dx
j
d
du du' du'
n
du' du' du' d
2ju—-.—'■ '--2/u—-—- --ju
dx
k
dx
k
dXj dx
k
dx
k
dx
}
- dx
;
f
du'
2
^
u
\dx
k
j

110
Abrasive Erosion
and
Corrosion of Hydraulic Machinery
-2v
d
dx.
y^k
&k j
+
-
d_
dx,
(ps)-2p
2...
^
2
d
z
u
dxjdx,
j
2v
d
dx
h
p
u
Hp
p,
du
7\
dx
+
2v
d
j
J
dx
v
,
, du
p
'
u
"Tx.
T\
k
J
t d
2
u'
f
_ , du' dp
k
_
-2vpu'---f-2vu'
^ P
-2p
p
e
P
"'
dx
2
k
1
dx. dx
v
„o
„ ,du\ dS
+
2Se + 2vu —-
+ ■
dx
k
dx
k
(3.32)
3.2 Closed Turbulent Equations
for
Liquid-Solid Two-
Phase Flow through Hydraulic Machinery
3.2.1 Closed Turbulence Model Using
the
Modeled Second
Correlation
It
is
necessary
to
apply
the
turbulence model
to
close
the
foregoing equations
of multiphase flow.
In
this session,
the
modeled second correlation terms
are
used
to
simulate
the
third order correlation term
and
others, such
as, the
term
containing
the
fluctuate pressure, which results
in
closing of Reynolds stresses
equations.
Modeled Turbulent Reynolds Stresses Equations for Liquid Phase
The modeled equations
of
the turbulent Reynolds stresses equations
for the
liquid phase,
i.e.,
equation (3.28)
is as
follows:
d d
^(P^
+
^PU^^^
+ p
v
+Yl
v
-**
+G
VM +Gw
(3.33)

Analysis and Numerical Simulation of Liquid-Solid Two-Phase Flow 111
where the gradient model, i.e., the Daly-Harlow model is used for the
turbulence diffusion term in the following form:
dx
k
vr K
'
J
'
] m
* '
1K
' dx
k
d \~ k -7-7 d rj-Ts , . <?
[C
s
p-u'
k
u'
l
—(u'
i
u'
J
)
+
J
u—-(u'
i
u'
j
)
ox
k
s ax
t
ax
t
77
77
»,.«,.w ^»w «,...»,
£
k
', has the same dimensions as that of the eddy
viscosity, fj,j, which reflects its anisotropy. The constant C
s
in this equation is
taken as 0.24.
The turbulence posses the local isotropy at the high Reynolds number
condition, the dissipation for different turbulence energy components are the
du'.
du'
same, that is, the term, —'-. , is zero at conditions of / *
j.
So the
dx
k
dx
k
turbulent energy dissipation can be defined as follows:
du'.
du' 2
e
v
=2
M
(-^.-^) = -S
ii
p
e
dx
k
dx
k
3
The correlation terms, which including the pressure fluctuation, can be
divided into three parts: the correlation between fluctuate velocity
components, the correlation between fluctuate velocity components and the
mean strains and the correlation between fluctuate velocity components and
buoyancy, which are modeled by the following n,
y
,, Il
jy2
and
Yl
jj3
in the
Launder-Rotta model:
n,=/>'
du\
du
>
\
3
+-
y
dx
k
dx
kJ
n
ff
.,+n,.
2
+n,
i3
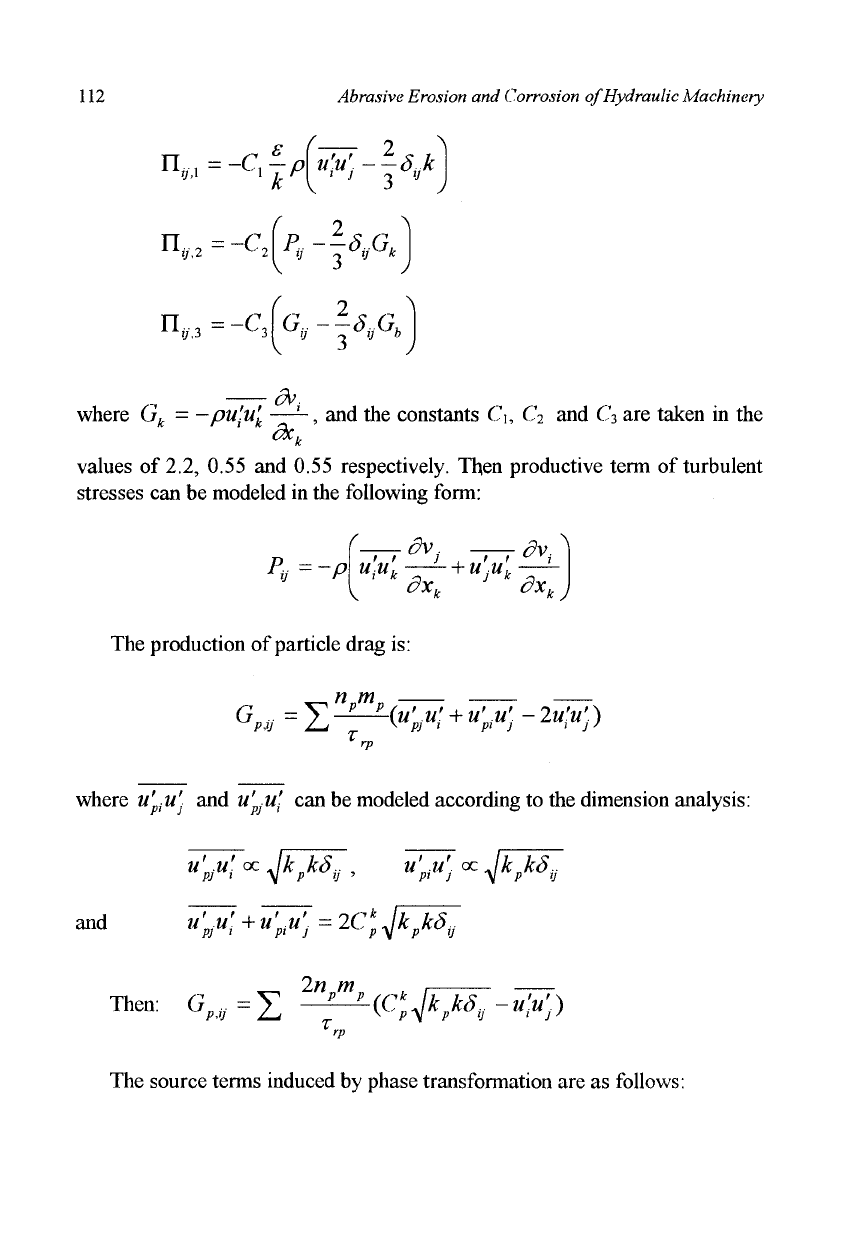
112
n„=-c,-„
Abrasive Erosion and Corrosion of Hydraulic Machinery
r
2
A
n,,
2
= -c
2
n
tfi3
= -Q
f
2 ^
v
'i;
VJ
jt
y
^
2 ^
eV.
where
G
k
= -pu\u'
k
—-, and the constants C\, C
2
and C
3
are taken in the
dx
k
values of 2.2, 0.55 and 0.55 respectively. Then productive term of turbulent
stresses can be modeled in the following form:
P* = ~P
dv
t
u[u[ —1-
+
u'ju'
k
dv
4
<i"k
dx^
dx,
k
J
The production of particle drag is:
njn
Grt^-^iuW
+
W-ZW)
where u'^u'. and u'
pj
u\ can be modeled according to the dimension analysis:
u;. u\
oc
^k
p
ks
v
, u;.«;
oc
Jk
p
ks
u
and
^
+
w>y
=
2Cj^M..
2A?
TYl
Then:
G
rt
=I
-^(CjJW^;)
The source terms induced by phase transformation are as follows:

Analysis and Numerical Simulation of Liquid-Solid Two-Phase Flow
113
G
RJI
= lulu]
■
S
And the constant C can be taken as 0.11.
Modeled Turbulent Kinetic Energy Equation and Turbulent Energy
Dissipation Rate Equation for Liquid Phase
The exact turbulent kinetic energy, k, equation for liquid phase can be
obtained from equations (3.28) through adding / =j.
d_
dt
a Z$ r ;3
(pu'
i
u'
i
)
+
-—(jw
kU
y.)
=
\p
U
'
k
u'.u\
+2p'u'
t
+
ft-r—(uy.) ]
dx dx
dx,,
—r—,
du
■2pu'
k
u —^-2ju
dx
L
f
du'^
\dx
k
j
Inm.
+
p P si I .,'.,'
y
p
y-uy)+2uys
(3.34)
Defining the turbulent kinetic energy k = v/v/ / 2, the modeled turbulent
kinetic energy, i.e., k equation can be deduced through introducing the
foregoing correlation terms:
(
p
k)+ (pu k) = —
at dx
}
. dx
j
^
'
k^-,dk^
pi... —u.u. —
c
s ' ' dx.
pu
j
.u
j
• J
du
i
dx.
+
n
P
m
P
r
v
(C
k
py
[k~^k-k)
+
2kS-ps (3.35)
where the constant C
k
is taken as 0.24, and the constant C
=0.11.
The modeled turbulent energy dissipation rate, i.e., s equation for liquid
phase can be also obtained by using the same method:
d d
d
(pS)
+
{pU,£) =
dt ^ dXj ^
J
' dXj
v
k -r~, ds
pi
r
—u,u
i
J
'
dx,
• J
s
+
—
k
C
,l i-pUjU'i
dx..
