Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

952 Part E Scattering Experiment

where θ

= 2u

and u

is the target binding en-

ergy. The function f rises rapidly for V <v

, reaching

a value near unity near V = v

and falling very slowly

thereafter. Tables of f for K- and L-shell ionization

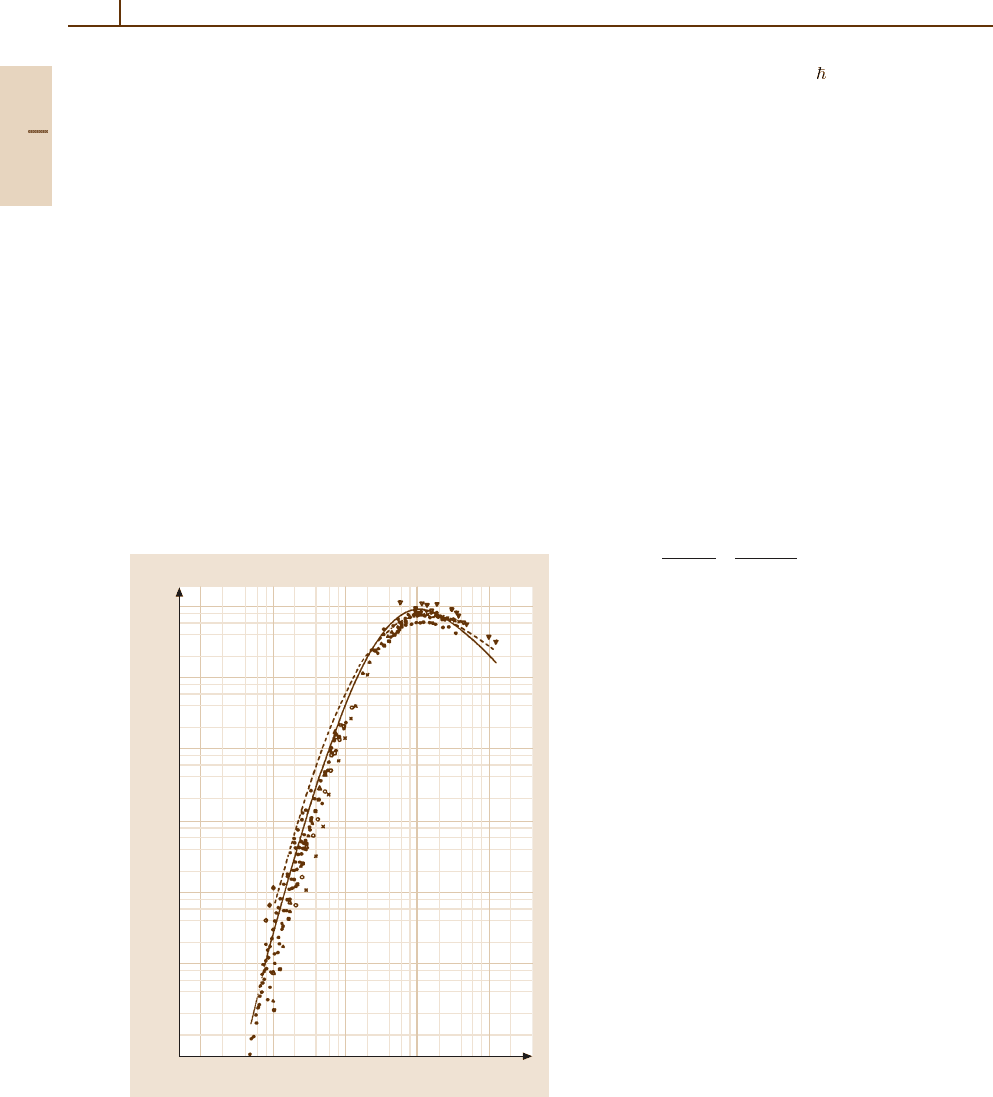
are given in [65.3, 4]. Figure 65.1 shows a compari-

son of experimental data for K vacancy production by

protons with PWBA calculations, and with a classical bi-

nary encounter approximation [65.12] for a large range

of proton data [65.6]. For larger Z

, corrections to the

PWBA and SCA must be made for the effective increase

of u

due to the presence of the projectile during the

ionization, for nuclear projectile deﬂection, for relativis-

tic corrections, and for the polarization of the electron

cloud, as reviewed in [65.13–17]. Total cross section

measurements for inner shell vacancy production in the

perturbative region are reviewed in [65.15, 16].

In the SCA treatment, the heavy particle motion

is taken to be classical, and the evolution of the elec-

tronic wave function under the inﬂuence of the projectile

ﬁeld is calculated by time-dependent perturbation the-

ory. The assumption of classical motion is valid if the

–19

–20

–21

–22

–23

–24

–25

–3

–2

–1

(keV

)

E/λU

Fig. 65.1 Comparison of experimental cross sections for

K-shell vacancy production with PWBA (dashed) and bi-

nary encounter (solid) theories. U

is the target binding

energy in keV and λ the projectile/electron mass ratio [65.6]

Bohr parameter K = 2Z

/( V ) is much larger than

unity [65.18]. If this condition is satisﬁed, the projec-

tile scattering angle can be associated with a particular b

through a classical deﬂection function. For K-shell ion-

ization, the action occurs typically at sufﬁciently small b

that a screened Coulomb potential is sufﬁcient for cal-

culating the deﬂection. In the absence of screening,

θ =r

/b,wherer

= Z

/E with θ and E expressed

in either the laboratory or c.m. system. Calculations for

K- and L-shell ionization have been carried out [65.10].

The typical ionization probability P(b) for V ∼ v

and

b = 0isP(0) ∼ (Z

)

.ForV <v

, P(b) decreases

with increasing b with a characteristic scale length of

= V/ω,theadiabatic radius,whereω is the transition

energy. For V >v

, P(b) cuts off near the K-shell radius

of the target. A more sophisticated relativistic SCA pro-

gram has been written [65.19], and is widely used for

calculating P(b), cross sections, and probabilities differ-

ential in ﬁnal electron energy and angle. Experimentally,

the probability P(b) for inner shell ionization can be

determined from

P(b) =

ω∆Ω



N[θ(b)]



(65.2)

where Y is the coincidence yield for the scattering of

N(θ) ions into a well-deﬁned angle θ(b) accompanied

by X-ray (or Auger electron) emission with ﬂuorescence

yield ω into a detector of efﬁciency  and solid angle ∆Ω

[65.20]. The necessary ω can be obtained from calcu-

lations for neutral targets [65.21](Chapt.62). However,

they must be corrected for changes due to extensive outer

shell ionization during the collision. Such corrections are

particularly important for targets with low ﬂuorescence

yields, for Z

below 30, and for collisions in which the

L-shell is nearly depleted in the collision [65.15,16]. Val-

ues of P(b) have been measured for many systems and

generally show good agreement (better than 10%) with

the SCA for fast light projectiles such as protons, with

increasing deviation as higher Z

or slower V are used

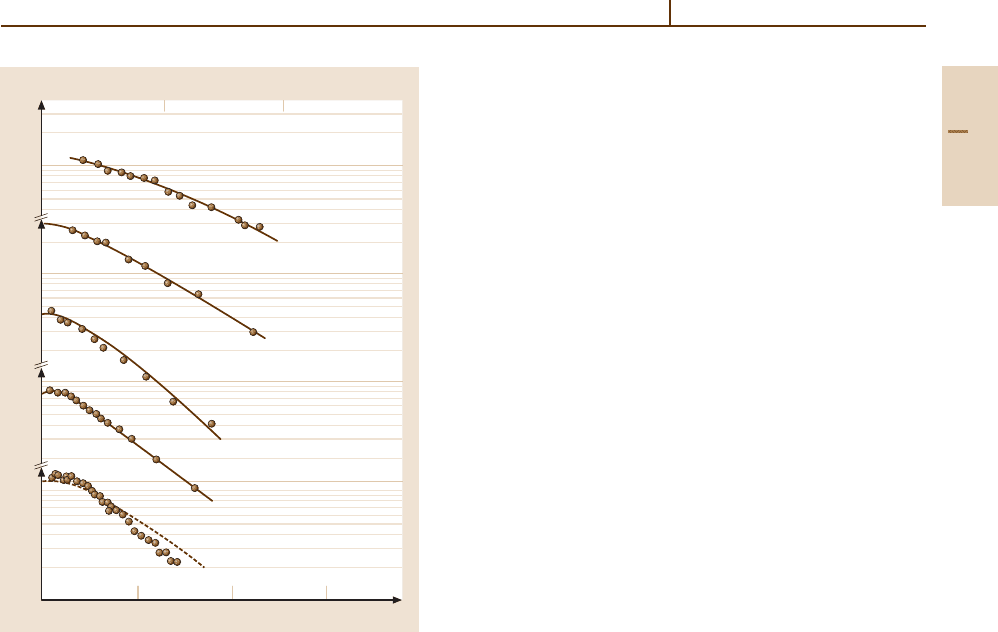
[65.22]. Examples of P(b) for K vacancy production for

several systems are shown in Fig. 65.2, showing the evo-

lution away from the SCA as the collision becomes less

perturbative.

Ionization of Light Target Atoms

Ionization of light target atoms by bare ion impact is

a particularly suitable process to study the atomic few-

body problem. In the case of an atomic hydrogen target

the collision represents a three-body system, i. e., the

simplest system for which the Schrödinger equation is

not analytically solvable. However, because of the ex-

Part E 65.1

Ion–Atom Collisions – High Energy 65.1 Basic One-Electron Processes 953

–3

1.0 2.0 3.0

b/r

P(b)/ Z

Projectile/Target

2.0

3.0

3.62

7.25

0.52

0.35

F(5+)/Ar

C(4+)/Ar

O(6+)/Cu

Be/Cu

p/Cu

SCA

Fig. 65.2 P(b) for K-shell vacancy production versus b/r

for several systems (see text). The ratio V/v

is desig-

nated as “V” in this ﬁgure. For protons p, agreement with

the SCA theory is found [65.10], while for higher Z

P(b) moves to larger impact parameters as one leaves the

perturbative region [65.22]

perimental difﬁculties associated with atomic hydrogen,

measurements with this target species are rare [65.23]

and experimental studies have focused on helium tar-

gets. Here, the collision still constitutes a relatively

simple four-body system. With regard to the few-body

problem, studies of ionization processes have the im-

portant advantage that, in contrast to pure excitation and

capture processes, the ﬁnal state involves at least three

independently moving particles.

Detailed information about the few-body dynamics

in a collision can be extracted from multiply differential

measurements. This can be accomplished by measur-

ing the kinematic properties (e.g., energy, momentum,

ejection angle) of one or more of the collision frag-

ments. The ﬁrst experimental multiply differential single

ionization cross sections were obtained by studying

the ionized electron spectra as a function of energy

and ejection angle. Such studies were reviewed by

Rudd et al. [65.24] and are discussed in more detail

in Sect. 65.3. More recently, complementary multiply

differential data were obtained by measuring projectile

energy-loss spectra as a function of scattering angle in

p+He collisions [65.25, 26].

A comprehensive picture of ionizing collisions can

be obtained from kinematically complete experiments.

In such a study the momentum vectors of all collision

fragments need to be determined. However, in the case

of single ionization it is sufﬁcient to directly measure

the momentum vectors of any two particles in the ﬁnal

state; the third one is then readily determined by mo-

mentum conservation. For ionization by electron impact,

this has been accomplished by momentum-analyzing

the scattered and the ionized electrons (for a review

see [65.27]). For ion impact, this approach is difﬁcult

because of the very small scattering angles and energy

losses (relative to the initial collision energy) resulting

from the large projectile mass. Consequently, the only

kinematically complete experiments involving a direct

projectile-momentum analysis were reported for light

ions at relatively low projectile energies [65.28]. For

heavy-ion impact at high projectile energies, in con-

trast, the complete determination of the ﬁnal space state

is only possible through a direct measurement of the

ionized electron and recoil-ion momenta [65.29].

The technology to measure recoil-ion momenta with

sufﬁcient resolution, and therefore to perform kinemat-

ically complete experiments for heavy-ion impact, has

only become available over the last decade (for re-

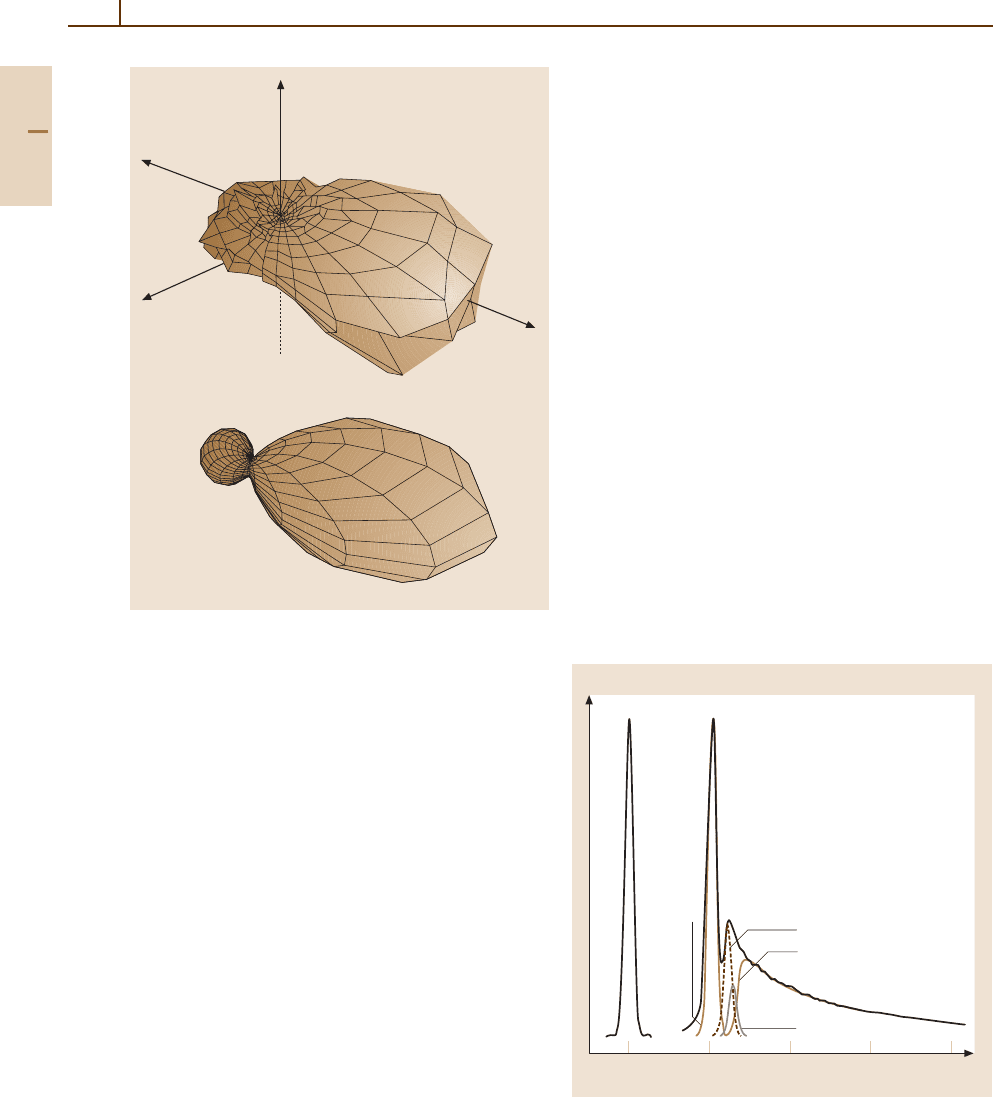
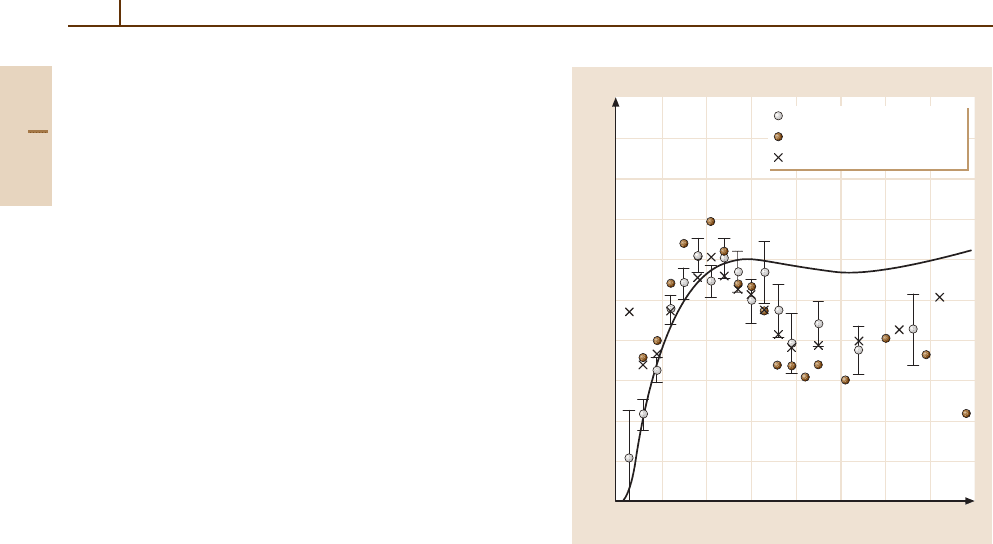
views, see [65.30–32]). Figure 65.3 shows measured

(top) and calculated (bottom) three-dimensional angu-

lar distributions of electrons ionized in 100 MeV/a.m.u.

+He collisions for fully determined kinematic con-

ditions [65.33]. The arrows labeled p

and q indicate

the direction of the initial projectile momentum and the

momentum transfer deﬁned as the difference between

and the ﬁnal projectile momentum p

.Thisplotis

rich in information about the dynamics of the ioniza-

tion process. The main feature is a pronounced peak in

the direction of q. It can be explained in terms of a bi-

nary interaction between the projectile and the electron,

i. e., a ﬁrst-order process, and is thus dubbed the “Bi-

nary Peak”. A second, signiﬁcantly smaller, structure is

a contribution centered on the direction of −q (called the

“Recoil Peak”). This has been interpreted as a two-step

mechanism where the electron is initially kicked by the

projectile in the direction of q and then backscattered by

the residual target ion by 180

◦

. Although this process in-

volves two interactions of the electron, it is nevertheless

a ﬁrst-order process in the projectile–target atom inter-

Part E 65.1

954 Part E Scattering Experiment

(z-axis)

Fig. 65.3 Three-dimensional angular distribution for fully

determined kinematic conditions of electrons ionized in

100 MeV/a.m.u. C

+He collisions. To p, experimental

data; bottom, CDW calculation (see text)

action. Therefore, as expected for this very large value

of η

= 100 (in a.u.), the ionization cross sections are

dominated by ﬁrst-order contributions.

The basic features of the data in Fig. 65.3 are

well reproduced even by the relatively simple ﬁrst

Born approximation (FBA). Furthermore, the calcula-

tion shown in the bottom of Fig. 65.3, which is based

on the more sophisticated continuum distorted wave ap-

proach (CDW)([65.35–37] see also Chapt. 52), yields

practically identical results to the FBA.IntheCDW

method, higher-order contributions are accounted for

in the ﬁnal-state scattering wavefunction. Apart from

this good overall agreement, a closer inspection of the

comparison between experiment and theory also reveals

some signiﬁcant discrepancies. While in the calculation

the Binary and Recoil peaks are sharply separated by

a minimum near the origin, in the data this minimum

is almost completely ﬁlled up giving rise to a “ring-

like” shape of the recoil peak. This was explained by

a higher-order ionization mechanism involving an in-

teraction between the projectile and the residual target

ion [65.33,37,38]. Although the contribution of this pro-

cess to the total cross section is negligible, it is a very

surprising result that for selected kinematic conditions

higher-order processes can be important even at large

projectile energies. A sobering conclusion of recent re-

search on ionization of light target atoms is that evenwell

inside the perturbativeregimethe atomic few-body prob-

lem is not nearly as well understood as was previously

assumed based on studies for restricted collision geom-

etries. At large perturbation, the lack of understanding

is dramatic [65.39].

Excitation

Inner shell excitation can be treated within the same

perturbative framework, which leads to a cross section

given in terms of the generalized oscillator strength for

the transition [65.40–42]. For inner shell vacancy pro-

duction by light projectiles, the excitation is generally

much smaller than the ionization, since the strongest os-

cillator strengths are to low-lying occupied orbitals, as

reviewed by Inokuti [65.41]. Excitation cross sections

can be deduced from photon production cross sections

and from inelastic energy loss experiments. An example

of the cross section for excitation of the n = 2levelofH

by protons, measured by the latter technique, is shown

in Fig. 65.4 [65.34].

0 10203040

Energy loss (eV)

Contributions of individual terms in dσ/dξ

σ(n =4)

σ(n =3)

Continuum terms

σ(n =2)

Fig. 65.4 Energy loss spectrum for 50 keV protons in

atomic hydrogen, showing excitation to discrete states in

H proceeding smoothly into ionization at the continuum

limit [65.34]

Part E 65.1

Ion–Atom Collisions – High Energy 65.1 Basic One-Electron Processes 955

Capture

As Z

is raised, the probability for direct trans-

fer of inner shell electrons from projectile to target

becomes competitive with, and can even exceed, that

for ionization of the target electron into the continuum.

The ﬁrst-order perturbation treatment for electron cap-

ture, given by Oppenheimer [65.43] and by Brinkman

and Kramers [65.44](OBK) ([65.11], p. 379) results in

a cross section per atom

OBK

= 2

π(Z

)

/5 V

, (65.3)

from a ﬁlled shell ν to all ﬁnal states n,where

β =



+2V



/ν

+ Z





/ν

− Z





(65.4)

Both the PWBA/SCA and the OBK cross sections

maximize near the matching velocity, but the OBK falls

off much more strongly with increasing V beyond this,

eventually falling as V

−12

, while the ionization cross

section only falls as V

−2

ln V .TheOBK amplitude for

capture is simply the momentum space overlap of the

initial wave function with the ﬁnal state wave func-

tion, where the latter is simply a bound state on the

projectile but moving at a velocity V relative to the

initial bound state. The integral is done only over the

transverse momentum, since the longitudinal momen-

tum transfer is ﬁxed by energy conservation [65.11].

This capture amplitude thus depends heavily on there

being enough momentum present in the initial and/or

ﬁnal wave function to enable the transfer, and the loss of

this match is what leads to the steep decrease in the OBK

cross section above velocity matching. Cross sections

for K-shell capture have been measured by detection of

K Auger electrons and K X-rays in coincidence with

charge capture by the projectiles [65.22, 45,46]. On the

basis of these and many other data on electron cap-

ture, the OBK is a factor of approximately three too

large [65.45–48]. This factor comes from a fundamental

failure of ﬁrst-order perturbation theory for electron cap-

ture. As pointed out already in 1927 by Thomas [65.49],

who proposed a classical two-collision mechanism for

capture, it is essential that the electron interacts with

both nuclei during the collision in order to be captured

(Chapt. 57). In quantum theories, this corresponds to the

fundamental need to include second-order terms (and

higher) in the capture amplitude. In the limit of large V,

the second-order cross section decreases more slowly

than the OBK term, as V

−10

, and thus is asymptotically

larger than the ﬁrst-order term [65.50]. At large V ,the

coefﬁcient of the V

−12

term, the dominant one at most

experimentally reachable V ,is0.29 times the OBK cross

section when the theory is carried out to second-order

in the projectile potential [65.50,51]. Roughly speaking,

this provides an explanation for the factor of three. Much

more sophisticated treatments of high velocity capture

are now available [65.52–60]. The underlying role of

the second-order scattering process was conﬁrmed ex-

perimentally by the detection of the Thomas peak in the

angular distribution of protons capturing electrons from

He and H [65.61,62](Chapt.57).

In spite of the basic importance of second-order

amplitudes in perturbative capture, the OBK gives an

excellent account of the relative contributions from and

to different ﬁnal shells over a large range of V above v

and is thus, when appropriately reduced, still useful as an

estimate for perturbative capture cross sections between

well deﬁned ν and n for large V .

For electron capture, as in the case of ionization (see

previous section), the development of recoil-ion mo-

mentum spectroscopy (RIMS) has enabled much more

detailed studies of the collision dynamics. The trans-

verse (perpendicular to the beam direction) recoil-ion

momentum component p

⊥

reﬂects the closeness of the

collision both relative to the target nucleus and the elec-

trons. The longitudinal (parallel to the beam direction)

component p

, on the other hand, is related to the internal

energy transfer Q in the collision by (in a.u.)

=−Q/V −nV/2 , (65.5)

where n is the number of captured electrons. A meas-

urement of p

is therefore equivalent to a measurement

of Q. The advantage over measuring Q from the projec-

tile energy loss is that at large collision energies a much

better energy resolution is achievable. A sample Q meas-

urement with RIMS is shown in Fig. 65.5 [65.63]. Very

recently, RIMS was applied to study capture processes

in collisions with an atomic hydrogen target [65.64].

This could be an important breakthrough in advancing

our understanding of the atomic few-body problem as it

opens the possibility to perform kinematically complete

experiments on the true three-body system X

Z+

+H,

where X can be any bare projectile.

65.1.2 Nonperturbative Processes

Fano–Lichten Model

When the collision becomes increasingly perturba-

tive, either due to a decreased V or increased Z

higher-order effects become generally more impor-

tant. One approach to account for such contributions

Part E 65.1

956 Part E Scattering Experiment

–3 –2 –1 0 1

Counts (arb. units)



rec

(a.u.)

0.25 MeVHe

+ He– – He

(n) + He

(n)

(1, 2) & (2, 1)

(n, n)=

(1, 1)

0.26 a.u.

FWHM

(1,3)&(3, 1)

(2, 2)

Fig. 65.5 Longitudinal momentum spectrum of recoil ions

from 0.25 MeVHe

capturing a single electron from a cold

He target, showing clear resolution of capture to n = 1 from

that which leaves target or projectile excited [65.63]

is the continuum distorted wave–eikonal initial state

(CDW-EIS)model ([65.35, 36, 65], see also Chapt. 52

and Sect. 65.1.1). The range of validity of CDW-EIS is

roughly given by Z

 1 [65.35]. Therefore, if the

perturbation is large due to the projectile charge, the col-

lision may still be treated perturbatively provided that

the collision energy is sufﬁciently large. Otherwise, the

perturbation treatment is replaced by a molecular orbital

treatment.

Fano and Lichten [65.67] pointed out that the ra-

tio V/v

can be small for inner orbitals even for V

of several a.u., and thus an adiabatic picture of the

collision holds. K vacancy production cross sections

become much larger than the perturbation treatments

above predict and extend to much larger b.Inthemo-

lecular orbital picture, the collision system is described

in terms of time-dependent molecular orbitals (MO)

formed when the inner shells of the systems overlap.

Vacancy production occurs due to rotational, radial, and

potential coupling terms between these orbitals during

the collision. The independent electron model is used,

but the results in any speciﬁc collision are quite sen-

sitive to the occupation numbers (or vacancies) in the

initial orbitals. These are very difﬁcult to control in

ion–atom collisions in solids and even problematic in

gases, since outer shell couplings can produce vacan-

cies at large internuclear distances which then enable

transfers at smaller distances. Numerous reviews of

the subject are available, including [65.68–72]. The

most famous MO ionization mechanism involves the

R = O

3p Cl

3s Cl

2p Ar

2s Ar

2p Cl

2s Cl

4fσ

ls Cl

ls Ar

R = ∞

lsσ

Radial

coup

Rot coup

2pπ

2pσ

Fig. 65.6 Schematic correlation diagram for the Cl

−

system, indicating the rotational coupling and radial coup-

lings important for K vacancy production and the 4fσ orbital

whose promotion leads to L vacancy production [65.66]

promotion of the 4fσ orbital in a symmetric collision

(Fig. 65.6), which promotes both target and projectile

L electrons to higher energies where they are easily

lost to the continuum during the collision. There are

now many treatments of inner shell vacancy produc-

tion mechanisms based on MO expansions (Chapts.

50, 51). For the case of K vacancy production in

quasisymmetric collisions, an important MO mecha-

nism is the transfer of L vacancies in the projectile

to the K-shell of the target through the rotational cou-

pling between 2pπ and 2pσ orbitals which correlate

to the L- and K-shells respectively of the separated

systems (Fig. 65.6) [65.73, 74]. The process can be

dynamically altered by the sharing at large b be-

tween L vacancies of target and projectile through

a radial coupling mechanism [65.75, 76]. This shar-

ing mechanism can also give rise to the direct transfer

of K vacancies from projectile to target (KK shar-

ing). In symmetric systems, the KK sharing results in

an oscillation of the K vacancy back and forth be-

tween target and projectile during the collision, and

leads to an oscillatory behavior of the transfer prob-

Part E 65.1

Ion–Atom Collisions – High Energy 65.2 Multi-Electron Processes 957

ability with V and b [65.77, 78]. Both of the above

vacancy production mechanisms are electron transfer

processes rather than direct ionization processes, in that

no inner shell electron need be liberated into the con-

tinuum. Between the perturbation region and the full

MO region the importance of transfer increases rela-

tive to ionization. While the MO correlation diagrams

and mechanisms are qualitatively useful, actual close

coupling calculations for both inner and outer shell

processes are often carried out using atomic orbitals

instead of molecular orbitals, as well as other basis

sets (Chapts. 50, 51).

65.2 Multi-Electron Processes

In a single collision between multi-electron partners,

two or more electrons may be simultaneously excited

or ionized. The electric ﬁelds created during a violent

ion–atom collision are so large that the probability of

such multi-electron processes can be of order unity.

While there are many similarities between ion–atom col-

lisions and the interaction of atoms with photons (X-rays

or short laser pulses) or electrons, the dominance of

multi-electron processes is very much less common in

the photon and electron cases. As an example, when

a K-shell electron is removed from a target atom by the

passage of a fast highly charged ion through its heart,

the probability that L-shell electrons will be removed

at the same time can be large. This gives rise to target

X-ray and Auger-electron spectra which are dominated

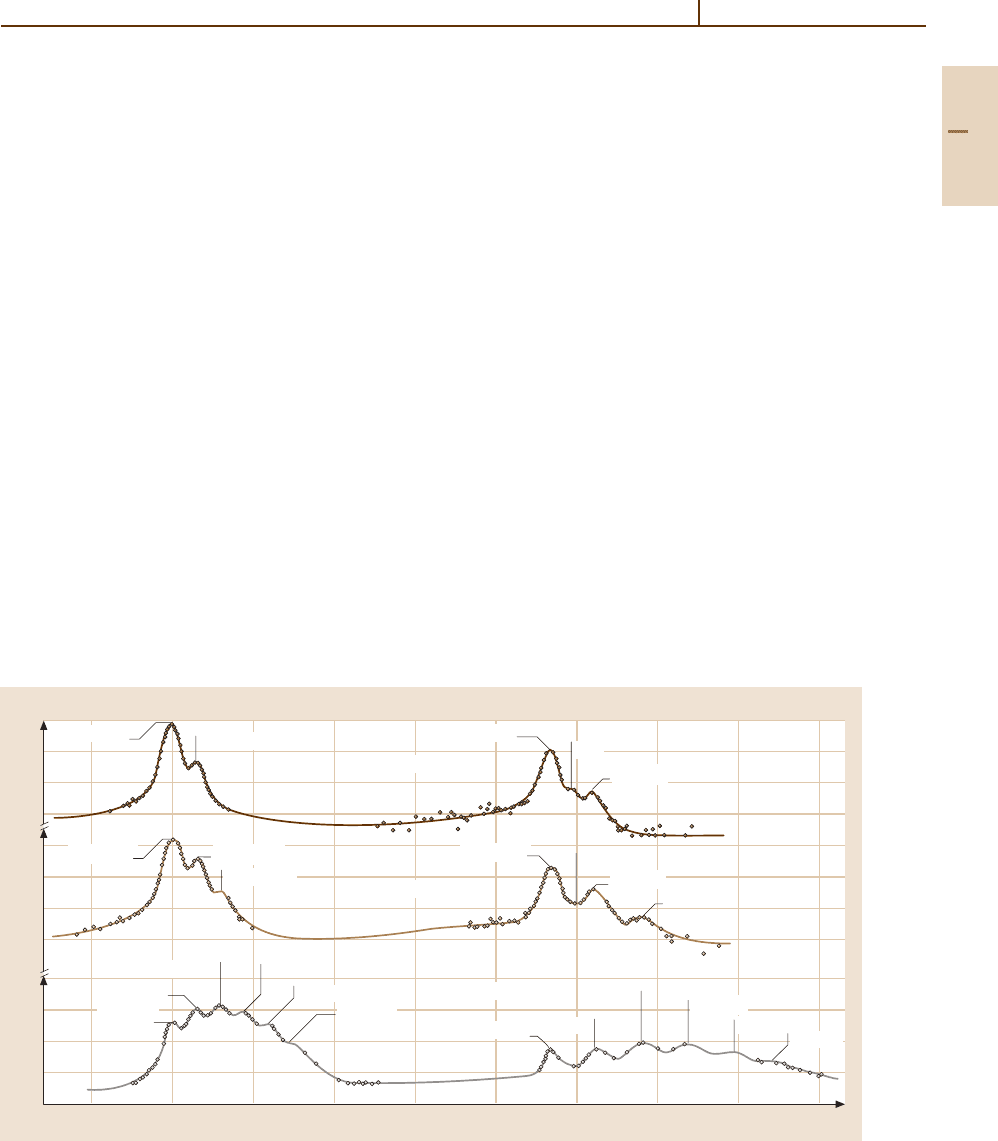
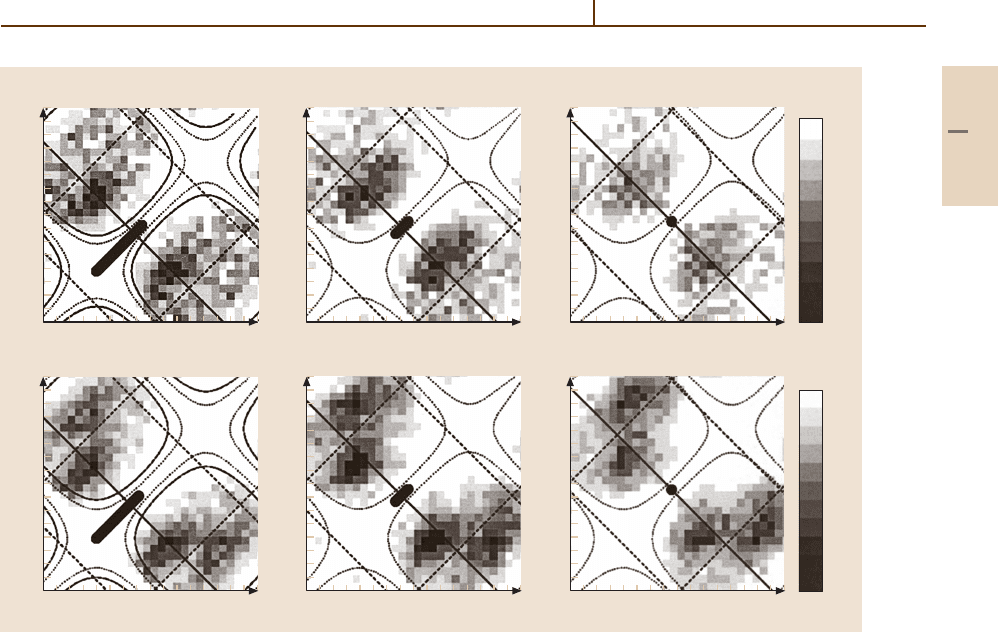
by satellite structure [65.20]. For example, the spectrum

2.80

Wavelength (Å)

2.70 2.60 2.50 2.40

Number of counts

Kα

1.2

(2p)

Kα

3.4

(2p)

+ Ti

= 0.8 MeV

= v

Kβ

1.3

(2p)

Kβ

Kβ(2p)

Kα

1.2

(2p)

Kα

3.4

(2p)

Kα

3.6

(2p)

+ Ti

= 3.2 MeV

Kβ

1.3

(2p)

Kβ

Kβ(2p)

Kα(2p)

+ Ti

= 30 MeV

Kβ(2p)

Fig. 65.7 K X-ray spectrum of Ti for various projectiles, showing dominance of multi-electron transitions when

K vacancies are collisionally produced by heavily ionizing projectiles



O beam



[65.79]

of X-rays from Ti bombarded by 30 MeV oxygen shows

that the production of the K vacancy is accompanied

by multiple L vacancy production, and that the domi-

nant K X-rays are those of systems which are missing

several L electrons [65.79](Fig.65.7).

When a gas target is used, the recoil target ion is

heavily ionized and/or excited electronically without re-

ceiving much translational kinetic energy. In the impulse

approximation the transverse momentum ∆ p

⊥

received

by the target from a projectile passing at impact par-

ameter b isgivenina.u.by∆ p

⊥

= 2Z

/bV.This

expression ignores the exchange of electronic trans-

lational momentum but gives a good estimate. The

resulting recoil energies are typically quite small, rang-

ing from thermal to a few eV. This subject has been

reviewed in [65.63,80]. These slow moving recoils have

Part E 65.2

958 Part E Scattering Experiment

been used to provide information about the primary col-

lision dynamics, and as secondary highly charged ions

from a fast-beam-pumped ion source. Such an ion source

has, for moderately charged ions, a high brightness

and has been used extensively for energy-gain measure-

ments. The primary recoil production process is difﬁcult

to treat without the independent electron model, and

even in this model the nonperturbative nature of the col-

lision makes the theory difﬁcult. The most successful

treatments have been the CTMC (see Chapt. 58)and

a solution of the Vlasov equation [65.64].

Studies of many-electron transitions in collisions

of bare projectiles with a He target are particularly

suitable to investigate the role of electron–electron cor-

relation effects because such collisions represent the

simplest systems where the electron–electron inter-

action is present. Such studies have been performed

extensively for a variety of processes, such as dou-

ble ionization, transfer-ionization, double excitation,

transfer-excitation, or double capture (for reviews

see [65.82–84]). It is common to distinguish (somewhat

artiﬁcially) between such correlations in the initial state,

the ﬁnal state, and during the transition (dynamic cor-

relation). From a theoretical point of view, the biggest

challenge is to describe electron–electron correlation

effects and the dynamics of the two-center potential

generated by the projectile and the target nucleus si-

multaneously with sufﬁcient accuracy.

In the case of double ionization, an experimental

method, based on the so-called correlation func-

tion [65.81], was developed to analyze electron–electron

correlations independently of the collision dynamics.

Here, a measured two-electron spectrum (for example

the momentum difference spectrum of both ionized elec-

trons) is normalized to the corresponding spectrum one

would obtain for two independent electrons. An example

of such a correlation function R isshowninFig.65.8 for

three very different collision systems (η

ranging from

0.05 to 100 and η

from 0.01 to 0.5ina.u.).Thesimilar-

ity in these three data sets illustrates that R is remarkably

insensitive to the collision dynamics. Rather, the shape

of R is determined predominantly by correlations in

the ﬁnal state [65.81, 85]. However, for selected kin-

ematic conditions, R can also be sensitive to initial-state

correlations [65.86]. Clear signatures of initial-state cor-

relations were found in the recoil-ion momentum spectra

for transfer-ionization [65.87].

Early attempts to identify dynamic correlations were

based on measurements of the ratio of double to single

ionization cross sections [65.88, 89]. From such stud-

ies, it was found that at small V double ionization

0.8

0.4

0.0

–0.4

–0.8

02468

p

–p

(a. u.)

100 MeV/amu C

+ He

3.6 MeV/AMU Au

53+

+ He

3.6 MeV/AMU Au

53+

+ Ne

Fig. 65.8 Correlation function R for double ionization in

the collisions indicated in the legend as a function of the

momentum difference between the two electrons [65.81].

R is deﬁned as R = I

exp

IEM

−1, where I

exp

is the directly

measured momentum spectrum and I

IEM

the one obtained

for independent electrons

is dominated by an uncorrelated mechanism involving

two independent interactions of the projectile with both

electrons. In contrast, at large V the double to single

ionization ratio asymptotically approaches a common

value for all collision systems [65.90]. This is indica-

tive of the dominance of ﬁrst-order double ionization

mechanisms, where the projectile interacts with only

one electron and the second electron is ionized through

an electron–electron correlation effect. This may either

be a rearrangement process of the target atom adjusting

to a new Hamiltonian (shake-off, an initial-state cor-

relation), or a direct interaction with the ﬁrst electron

(i. e., dynamic correlation). However, a recent nearly

kinematically complete experiment on double ioniza-

tion in p + He collisions revealed that even at large V

higher-order contributions are not negligible [65.91].

In Fig. 65.9 the ejection angles of both electrons are

plotted against each other for almost completely deter-

mined kinematics. For comparison, the bottom part of

Fig. 65.9 shows the corresponding spectra for electron

impact at the same V [65.92]. For both projectiles, the

basic features of these spectra are determined by the

Part E 65.2

Ion–Atom Collisions – High Energy 65.3 Electron Spectra in Ion–Atom Collisions 959

270

225

180

135

–45

–90

–90 –45 0 45 90 135 180 225 270

270

225

180

135

–45

–90

–90 –45 0 45 90 135 180 225 270

270

225

180

135

–45

–90

–90 –45 0 45 90 135 180 225 270

270

225

180

135

–45

–90

–90 –45 0 45 90 135 180 225 270

270

225

180

135

–45

–90

–90 –45 0 45 90 135 180 225 270

270

225

180

135

–45

–90

–90 –45 0 45 90 135 180 225 270

Fig. 65.9a–f Differential double ionization cross sections in 6 MeV p +He (top)and2keVe

−

+He (bottom) collisions

as a function of the polar emission angle of both electrons, which are emitted into the scattering plane. The electrons have

equal energy and data are shown for small (left), medium (center), and large momentum transfers (right) [65.91]

electric dipole selection rules, which again is indica-

tive of dominating ﬁrst-order contributions. However,

a closer inspection of the comparison between the pro-

ton and electron impact data shows some non-negligible

differences. Since in a ﬁrst-order treatment the cross sec-

tions should be identical for both projectile species, this

demonstrates that higher-order contributions cannot be

ignored.

65.3 Electron Spectra in Ion–Atom Collisions

65.3.1 General Characteristics

An ionizing collision between a single ion and a neutral

atom ejects electrons into the continuum via two major

processes. Electrons ejected during the collision form

broad features or continua, and are traditionally referred

to as delta rays; electrons ejected after the collisions

from the Auger decay of vacancies created during the

collision form sharp lines in the spectra. The distribu-

tions of energy and angle of all electrons determine the

electronic stopping power and characteristics of track

formation of ions in matter (Chapt. 91), and the study

of these distributions in the binary encounter of one ion

with one atom form the basis of any detailed understand-

ing of these averaged quantities. Figure 65.10 shows

a typical electron spectrum from the collision of a fast

O ion with O

[65.93,94]. Electrons from the projectile

can be identiﬁed in the cusp peak (electron loss, P) or

ELC, and the O-K-Auger (P) peak. Electrons from the

target include the soft (large b) collision electrons (T)

which are ejected directly by Coulomb ionization by

the projectile, the binary collision (or encounter) elec-

trons coming from hard collisions between projectile and

quasifree target electrons, and the target O-K-Auger (T)

Part E 65.3

960 Part E Scattering Experiment

01234

Cross section × Electron energy (10

–17

/sr)

Electron energy (keV)

25°

30°

40°

90°

30 MeV 0

on O

Soft collisions (T)

O–K Auger (T)

Electron

loss (P)

O–K

Auger (P)

Binary

collisions (T)

180 190 200 210 220 230 240 250 260

(10

–20

/eV sr)d

σ/ddε

dσ/d

(10

–18

/sr)

Electron energy (eV)

2l2l

2 1

2s2p

2 1

D 2s2p

2 1

2l3l

2l4l

2l5l

2lnl Series limit

3.91 MeV B

+ H

–

+ B

(1s)

Fig. 65.10 Electron spectrum from 30 MeV O on molecular

oxygen. See text for explanation of features [65.93,94]

electrons. The electron loss peak is widely called the

cusp peak because the doubly differential cross section

in the laboratory d

σ/ dE dΩ becomes inﬁnite, in prin-

ciple, if it is ﬁnite in the projectile frame. In general, this

peak may also contain capture to the continuum. All of

these features have been heavily studied; some reviews

are [65.95, 96]. Capture to the continuum [65.96]isan

extension of normal capture into the continuum of the

projectile, and is not a weak process. Both it and ELC

produce a heavy density of events in the electron mo-

mentum space centered on the projectile velocity vector,

and thus appear strongly only at or near zero degrees in

the laboratory and at v

 V .

The binary encounter electrons at forward angles

occur at v

∼

2V . For relatively slow collisions it was

found that the ELC and binary peaks are just part of

a more general and complex structure of the electron

spectra [65.98]. Additional peaks in the forward direc-

tion were found for v

∼

nV,wheren in principle can be

any integer number. These structures reﬂect a “bounc-

ing back and forth” (known as Fermi shuttle) between

the projectile and the target core before the electron

eventually gets ejected from the collision system.

In electron spectra for molecular targets, additional

structures were found that were not observed for atomic

targets [65.99]. These were initially interpreted as an

interference effect. The electronic wavefunction has

maxima at the atomic centers of the molecule. Since

in the experiment it cannot be distinguished from which

center the electron is ionized, both possibilities have

to be treated coherently. However, more recent studies

showed that at small electron energies the structures in

the electron spectra reﬂect vibrational excitation of the

molecule [65.100].

65.3.2 High Resolution Measurements

The Auger electron spectra provide detailed informa-

tion about inner shell vacancy production mechanisms.

Fig. 65.11 High resolution Auger electron spectrum from

H-like B on H

, showing resolved lines from doubly ex-

cited projectile states lying on top of a continuum due to

electron elastic scattering [65.97]. The bottom part shows

an R-matrix calculation which does not account for the ex-

perimental resolution. The smooth line in the upper ﬁgure is

the R-matrix calculation convoluted with the experimental

spectrometer resolution

Part E 65.3

Ion–Atom Collisions – High Energy 65.4 Quasi-Free Electron Processes in Ion–Atom Collisions 961

When coupled with ﬂuorescence yields, Auger elec-

tron production probabilities and cross sections can be

converted into the corresponding quantities for vacancy

production [65.15, 95]. This is best done when sufﬁ-

cient resolution can be obtained to isolate individual

Auger lines. The Auger spectra in ion–atom collisions

are often completely different from those obtained from

electron or photon bombardment because of the multiple

outer shell ionization which attends the inner shell va-

cancy producing event, in close analogy to X-ray spectra

(see previous section). Projectile Auger electron spectra

suffer from kinematic broadening due to the ﬁnite solid

angle of the spectrometer and velocity of the emitter, but

at 0

◦

to the beam this problem vanishes, and the reso-

lution in the emitter frame is actually enhanced by the

projectile motion, such that for electrons with eV ener-

gies in the projectile frame, resolutions in the meV region

are possible [65.101,102]. The highest resolution Auger

lines from ion–atom collisions has been done on the pro-

jectiles. A sample spectrum is shown in Fig. 65.11.From

such high resolution spectra, one-electron processes in

which one electron is excited, captured or ionized can

be distinguished from the conﬁguration of the emitting

state.

65.4 Quasi-Free Electron Processes in Ion–Atom Collisions

At sufﬁciently low V , those electrons not actively in-

volved in a transition play only a passive role in

screening the Coulomb potential between the nu-

clei, and thereby create a coherent effective potential

for their motion. However, at high V the colliding

electrons begin behaving as incoherent quasifree par-

ticles capable of inducing transitions directly via the

electron–electron interaction. Such processes signal

their presence through their free-particle kinematics,

as if the parent nucleus were not present. For exam-

ple, a projectile ionization process requiring energy U

has a threshold at

 U, in collisions with light

targets where the quasifree picture is meaningful. The

threshold is not sharp, due to the momentum dis-

tribution or Compton proﬁle of the target electrons.

Within the impulse approximation, the cross section

for any free electron process can be related to the cor-

responding cross section for the ion–atom process by

folding the free electron cross section into the Compton

proﬁle [65.97,103, 104].

65.4.1 Radiative Electron Capture

The ﬁrst quasifree electron process to be observed was

radiative electron capture (REC), the radiative capture

of a free electron by an ion. Conservation of energy

and momentum is achieved by the emission of a photon

which carries away the binding energy. The cross sec-

tion exceeds that for bound state capture at high V .

Radiative electron capture was observed through the

X-ray spectra from fast heavy projectiles for which the

electrons of light targets appear to be ‘quasi-free’. The

corresponding free electron process was seen [65.105]

and has recently been heavily studied in EBIT [65.106],

cooler [65.107], and storage rings [65.108]. Total cross

sections for REC have also been deduced from meas-

ured total capture cross sections at large V where REC

dominates bound state capture [65.109]. At high vel-

ocities, the cross section for radiative capture to the

K-shell of a bare projectile is given approximately





−2

+κ

−4



×2.1×10

−22

, (65.6)

where [65.110] κ =

√

, E

is the binding en-

ergy of the captured electron, E

the energy of the

initial electron in the ion frame and n the princi-

pal quantum number of the captured electron. The

theory seems to be in good agreement with experi-

ment for capture to all shells of fast bare projectiles,

although a small unexplained discrepancy between

theory and experiment exists for capture to the

K-shell [65.108].

65.4.2 Resonant Transfer and Excitation

Dielectronic recombination in electron–ion collisions

is the process whereby an incident electron excites

one target electron and, having suffered a correspond-

ing energy loss, drops into a bound state on the

projectile (Chapt. 55). If the doubly excited state so

populated decays radiatively, resonant radiative recom-

bination is achieved (DR); if it Auger decays, resonant

elastic scattering has occurred. The process has long

been known to be important as a recombination pro-

cess in hot plasmas [65.111], but was not observed

in the laboratory until 1983 [65.112–114]. The corres-

ponding ion–atom process, known as resonant transfer

and excitation (RTE) was seen a bit earlier by Tanis

et al. [65.115]. (See [65.116, 117] for reviews of both

DR and RTE.)

Part E 65.4