Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics
Подождите немного. Документ загружается.


556 Part C Molecules
and thence to the reactance matrix K through
S=
1+ iK
1− iK
.
(36.6)
The elements of the K matrix are real. Conservation of
the incident flux of particles requires that
jΩ
|S( jΩ, j
Ω
)|
2
= 1 . (36.7)
Micro-reversibility (time-reversal symmetry) implies
that the S matrix is symmetric,
S( jΩ, j
Ω
) = S( j
Ω
, jΩ) ,
and hence
σ( j ← j
)k
2
j
ω
j
= σ( j
← j)k
2
j
ω
j
. (36.8)
The thermally averaged (Maxwellian) rate coefficient
is
σv
j← j
=
8k
B
T
πµ
1
2
∞
0
x
j
σ( j ← j
)e
−x
j
dx
j
,
(36.9)
where x
j
= µv
2
j
/2k
B
T, v
j
being the relative colli-
sion velocity; k
B
is Boltzmann’s constant, and
(8k
B
T/πµ)
1
2
may be identified with the mean thermal
velocity at temperature T.From(36.8)and(36.9),
σv
j← j
ω
j
exp(−
j
/k
B
T)
=σv
j
← j
ω
j
exp(−
j
/k
B
T), (36.10)
where
j
,
j
denote the energies of the states
j
, j with respect to the reference level. Equation
(36.10) relates the rate coefficients of inverse tran-
sitions to their relative degeneracies and excitation
energies.
36.2 Semiclassical Method
If the collision dynamics are formulated using elem-
ents of both classical and quantum mechanics, then the
method is called “semiclassical”. Thus, the relative mo-
tion might be described by a classical trajectory, whilst
internal degrees of freedom (rotation, vibration, ...)
are quantized. The de Broglie wavelength associated
with the linear motion of a proton attains the Bohr
radius at a collision energy of 0.29 eV, and a classi-
cal trajectory is a good approximation at much higher
energies.
The introduction of a classical trajectory leads to
a time-dependent Hamiltonian, and Schrödinger’s equa-
tion may be reduced to a set of coupled, first-order
differential equations of the form
i
˙
a = Va ,
(36.11)
where a is a column vector of transition amplitudes
and
˙
a is the vector of their time derivatives. The square
matrix V is the interaction matrix, whose elements in-
corporate oscillatory factors of the type exp[(
j
−
j
)t].
The trajectory is taken to be symmetric about the
point of closest approach, t = 0, and a is initialized
through
a
j
→ δ
j
j
as t →−∞.
The differential equations (36.11) may be integrated
numerically, and the transition probabilities derived
from
P
b
( j ← j
) →|a
j
(b)|
2
as t →∞.
The cross sections are given by (36.1).
36.3 Quantal Method
The usual approach to nonreactive scattering [36.1]is
based on the Born–Oppenheimer approximation. The
interaction potential V is taken to be a known func-
tion of the nuclear coordinates, the electronic energy
being minimized for each geometry and separation of
target and projectile. The total Hamiltonian may then be
written
H =−
1
2µ
2
R
+h
1
(x
1
) + h
2
(x
2
)
+ V(R, x
1
, x
2
), (36.12)
Part C 36.3

Nonreactive Scattering 36.5 Coordinate Systems 557
where the first term represents the relative kinetic energy
of the target and projectile, and h
1
, h
2
are functions
of the intramolecular nuclear coordinates x
1
, x
2
.The
eigenfunctions ψ
1
,ψ
2
of h
1
, h
2
describe the vibrational
and rotational motions of the isolated molecules and
form a basis for expanding the total wave function Ψ of
the system:
Ψ(R, x
1
, x
2
) =
α
1
α
2
m
F(α
1
α
2
m|R)
R
× Y
m
(Θ, Φ)ψ
1
(α
1
|x
1
)ψ
2
(α
2
|x
2
).
(36.13)
In (36.13), α
1
,α
2
denote the sets of quantum numbers
required to specify the states of the isolated molecules,
and Y
m
(Θ, Φ) is a spherical harmonic function of
the angular coordinates of the intermolecular vector R.
F(α
1
α
2
m|R) are R-dependent expansion coefficients
which are solutions of the Schrödinger equation
(H − E)Ψ = 0 .
(36.14)
These solutions may be arranged as the columns of
a square matrix, F(R), in which each column is labelled
by a different initial scattering state. The radial functions
must satisfy the physical boundary conditions,
F(R) → 0 as R → 0
F(R) → J(R) A− N(R)B as R →∞,
where J and N are diagonal matrices whose non-
vanishing elements are given by
J
ii
= k
1
2
i
Rj
(k
i
R) (36.15)
N
ii
= k
1
2
i
Rn
(k
i
R), (36.16)
and j
, n
are spherical Bessel functions of the first,
second kinds; k
i
is the wave number in channel i (a given
set of values of the quantum numbers α
1
α
2
m).The
reactance matrix,
K = BA
−1
, (36.17)
yields the state-to-state cross sections.
36.4 Symmetries and Conservation Laws
The expansion of the total wave function, (36.13),
does not explicitly incorporate the invariance of the
Hamiltonian under an arbitrary rotation in space or
reflection in the coordinate origin. The Hamiltonian
commutes with J
2
,whereJ is the total angular momen-
tum, and any component of J, J
x
, J
y
, or J
z
, although
these components do not commute amongst themselves.
Eigenfunctions of H may, therefore, be chosen to be si-
multaneous eigenfunctions of J
2
and (conventionally)
J
z
, with eigenvalues J(J + 1) and M.If j
1
and j
2
are
the angular momenta of the isolated molecules, then
j
12
= j
1
+ j
2
is their resultant and
J = j
12
+ ,
where denotes the relative angular momentum of the
two molecules. The coupling of the angular momenta
to the multipolar expansion of the electromagnetic field
gives rise to collisional selection rules.
The parity operator, P, reflects the coordinates in the
origin. Because two successive operations with Prestore
the original values of the coordinates, the corresponding
eigenvalue p satisfies the equation p
2
= 1, or p =±1.
For electromagnetic interactions, the commutation of P
and H implies conservation of the parity of the system.
If one takes advantage of the conservation laws asso-
ciated with these symmetries of the system, substantial
savings in computing time can be made: only one value
of the total angular momentum and of the parity need to
be considered simultaneously.
36.5 Coordinate Systems
The natural choice of coordinate system in which to
express the interaction potential, V(R, x
1
, x
2
), is a body-
fixed (BF) system in which the z-axis coincides with the
direction of the intermolecular vector R = (R,Θ,Φ).
A rotation of the space-fixed (SF) coordinate system
through the Euler angles (Φ, Θ, 0) generates such a BF
frame. The intramolecular coordinates x
1
, x
2
must then
be expressed relative to the BF frame, as must the
Laplacian operator
2
R
which appears in the expres-
sion for the total Hamiltonian, (36.12). The latter may
Part C 36.5
558 Part C Molecules
be written as
2
R
=
1
R
∂
2
∂R
2
R−
2
R
2
=
1
R
∂
2
∂R
2
R−
(J− j
12
)
2
R
2
, (36.18)
which are the forms suitable for calculations in SF and
BF coordinates, respectively.
A unitary transformation relates the normalized
eigenfunctions of a given parity in SF and BF coor-
dinates. In Dirac notation,
| j
12
JM
SF
=
¯
Ω
| j
12
¯
ΩJM
BF
j
12
¯
ΩJM | j
12
JM, (36.19)
where
¯
Ω =|Ω| and Ω is the projection of J on the
BF z-axis. As the projection of on the intermolecular
axis is zero, Ω is also the projection of j
12
on the BF
z-axis. The absolute value of Ω appears in the transfor-
mation because | j
12
± ΩJM are not eigenfunctions of
the parity operator P, whereas the linear combinations
j
12
¯
ΩJM
=
| j
12
ΩJM +| j
12
− ΩJM
2
1 + δ
¯
Ω
0
1
2
( =±1) are eigenfunctions of P. The factor [2(1 +
δ
¯
Ω0
)]
1
2
ensures the correct normalization of these func-
tions. The elements of the matrix which performs the
unitary transformation (36.19)are
j
12
¯
ΩJM | j
12
JM
=
2(2 + 1)
(1 + δ
¯
Ω0
)(2J + 1)
1
2
C
j
12
J
¯
Ω0
¯
Ω
, (36.20)
where C
j
12
J
¯
Ω0
¯
Ω
is a Clebsch–Gordan coefficient.
36.6 Scattering Equations
Schrödinger’s equation for the scattering system
may be reduced to a set of coupled, ordinary,
second-order differential equations for the radial
functions F(R). Expressed in matrix form, they be-
come
1
d
2
dR
2
+ W(R)
F(R) = 0 . (36.21)
There exists a set of equations (36.21) for each value of
the total angular momentum J and parity p (Sect. 36.4).
The matrix W may be written
W(R) = k
2
− 2µV
eff
, (36.22)
where k
2
is a diagonal matrix whose non-vanishing
elements are
k
2
α
1
α
2
= 2µ
E −
α
1
−
α
2
.
(36.23)
k
α
1
α
2
is the wave number at infinite separation (R→∞)
when the molecules are in eigenstates α
1
,α
2
with
eigenenergies
α
1
,
α
2
. V
eff
is the matrix of the effective
potential,
V
eff
= V(R, x
1
, x
2
) +
2
2µR
2
, (36.24)
in which V is the interaction potential and
2
/
2µR
2
may be identified with the centrifugal potential. There
exist standard computer codes for solving equations of
the form (36.21) [36.2,3].
36.7 Matrix Elements
36.7.1 Centrifugal Potential
When evaluated in the SF frame, the matrix of the
centrifugal potential is diagonal, with non-vanishing
elements ( + 1)
2µR
2
.IntheBF frame, the diago-
nal elements are [see (36.18)]
j
12
¯
ΩJM |(J− j
12
)
2
/2µR
2
| j
12
¯
ΩJM
=
J(J + 1) + j
12
( j
12
+ 1) − 2
¯
Ω
2
/
2µR
2
,
(36.25)
and, in addition, there are off-diagonal elements
j
12
¯
ΩJM |(J− j
12
)
2
/2µR
2
| j
12
¯
Ω ± 1JM
=−
1 + δ
¯
Ω0
1 + δ
¯
Ω±1,0
× [J(J + 1) −
¯
Ω(
¯
Ω ± 1)]
× [ j
12
( j
12
+ 1) −
¯
Ω(
¯
Ω ± 1)]
1
2
/
2µR
2
.
(36.26)
The matrix elements (36.26), which are off-diagonal in
¯
Ω, are associated with the rotation in space of the BF
Part C 36.7
Nonreactive Scattering 36.7 Matrix Elements 559
coordinate system (Coriolis coupling). In the “coupled
states” approximation [36.4], the off-diagonal elem-
ents (36.26) are neglected, and the diagonal elements
(36.25) are often replaced by their SF equivalent form
( + 1)/(2µR
2
). The matrix of the interaction poten-
tial, on the other hand, continues to be evaluated in BF
coordinates. The net effect of these approximations is to
ignore the rotation of the BF frame in the course of the
collision, and the associated dynamical terms.
36.7.2 Interaction Potential
The interaction potential is usually expressed and com-
puted in BF coordinates. For the purposes of the analysis,
it is convenient to derive a multipolar expansion of the
potential from a least-squares fit to the original data
points. If the collision calculations are being done in the
BF frame, the potential matrix elements may be eval-
uated directly. However, if the SF frame is to be used,
the potential expansion must first be transformed into
SF form.
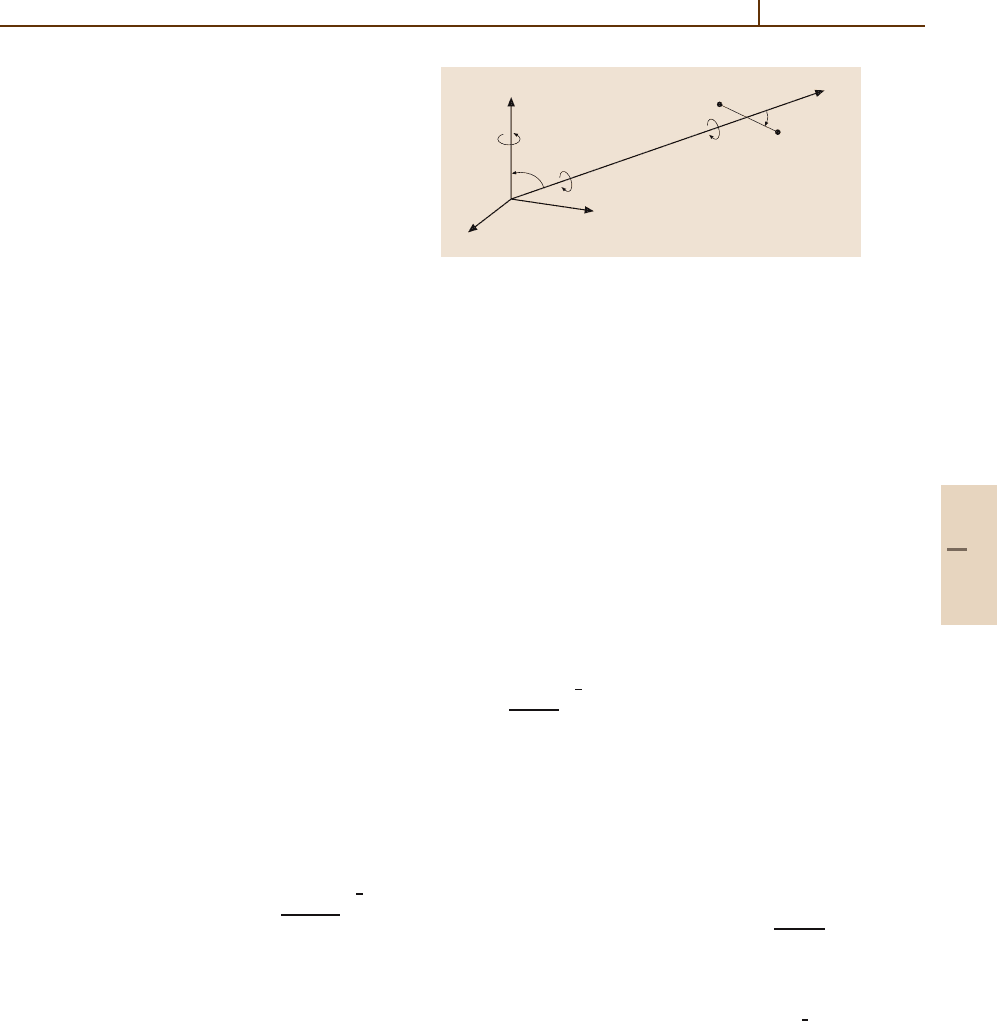
Consider the interaction between a symmetric top,
such as ammonia (NH
3
), and a rigid rotor, such as
H
2
[36.5, 6]. This complicated example serves as
a paradigm, and simpler cases may be derived by reduc-
tion. In the BF frame, the potential can be expanded as
V
R,
ˆ
ω
1
,
ˆ
r
2
=
λ
1
λ
2
µν
v
λ
1
λ
2
µν
(R)
× D
λ
1
µν
ˆ
ω
1
Y
λ
2
−ν
ˆ
r
2
,
(36.27)
where the Euler angles
ˆ
ω
1
=
φ
1
,θ
1
,ψ
1
determine
the orientation of the principal axes of the top and
ˆ
r
2
=
θ
2
,φ
2
the orientation of the axis of the rotor
(Fig. 36.2). Expanding the rotation matrix element D
λ
1
µν
and the spherical harmonic Y
λ
2
−ν
,(36.27) becomes
V
R,
ˆ
ω
1
,
ˆ
r
2
=
λ
1
λ
2
µν
v
λ
1
λ
2
µν
(R)
2λ
2
+ 1
4π
1
2
×e
iµψ
1
d
λ
1
µν
θ
1
e
iνφ
1
d
λ
2
0−ν
θ
2
e
−iνφ
2
(36.28)
where
d
j
m
m
(β) =jm
|exp(iβJ
y
)| jm (36.29)
according to the definition in [36.7]. We note that the
d
j
m
m
are real. The combination of positive and negative
values of the index ν in (36.28) reflects the invariance
of the potential under rotations about the intermolecu-
z⬙ z⬘
x⬙
y⬙
θ⬘
1
θ⬘
2
ψ⬘
1
⬘
1
⬘
2
φ
φ
Fig. 36.2 The body fixed coordinate system: scattering of
a rigid rotor and a symmetric top
lar axis
alternatively, its dependence on the difference
between φ
1
and φ
2
.InSF coordinates, the potential
becomes
V(R,
ˆ
ω
1
,
ˆ
r
2
)
=
λ
1
λ
2
λµ
v
λ
1
λ
2
λµ
(R)
×
m
1
m
2
C
λ
1
λ
2
λ
m
1
m
2
m
D
λ
1
µm
1
ˆ
ω
1
Y
λ
2
m
2
ˆ
r
2
Y
∗
λm
ˆ
R
.
(36.30)
The expansion coefficients in the SF and BF frames are
related by
v
λ
1
λ
2
λµ
(R)
=
4π
2λ + 1
1
2
ν≥0
C
λ
1
λ
2
λ
ν−ν0
(1 + δ
ν0
)
−1
×
v
λ
1
λ
2
µν
(R) + (−1)
λ
1
+λ
2
+λ
v
λ
1
λ
2
µ−ν
(R)
.
(36.31)
The matrix elements of the potential given by (36.30)
are
j
1
kj
2
j
12
JM
V
R,
ˆ
ω
1
,
ˆ
r
2
j
1
k
j
2
j
12
JM
=
λ
1
λ
2
λµ
v
λ
1
λ
2
λµ
(R)(−1)
j
1
+ j
2
+ j
12
+k
−J
2λ + 1
4π
×
(2 j
1
+ 1)(2 j
2
+ 1)(2 j
12
+ 1)(2 + 1)(2λ
2
+ 1)
×
2
+ 1
2 j
12
+ 1
2 j
2
+ 1
2 j
1
+ 1
1
2
×
λ
000
λ
2
j
2
j
2
000
λ
1
j
1
j
1
µ k −k
×
λ
j
12
j
12
J
j
12
j
2
j
1
j
12
j
2
j
1
λλ
2
λ
1
(36.32)
Part C 36.7
560 Part C Molecules
where k , k
denote the projection of j
1
, j
1
on the sym-
metry axis of the symmetric top;
···
···
is a Wigner
3 j-,
···
···
a6j-, and
···
···
···
a9j-coefficient. The po-
tential matrix elements for other important cases may
be derived from (36.32). Rigid rotor-rigid rotor [36.8]
obtains when k = µ = 0, and atom-rigid rotor when, ad-
ditionally, j
1
= λ
1
= 0. References to numerical results
for specific systems have been compiled in Appendix 2
of [36.9].
In order to exploit conservation of the parity of the
total system, it is necessary to use symmetry adapted
rotational eigenfunctions
j
1
¯
kmη
=
| j
1
km +η| j
1
− km
2
1 + δ
¯
k0
1
2
, (36.33)
where
¯
k is the absolute magnitude of the projection
of j
1
on the symmetry axis of the top. The par-
ity of the total wave function
j
1
¯
kη j
2
j
12
JM
is then
p = η(−1)
j
1
+ j
2
++
¯
k
and is conserved during the col-
lision. This fact enables the coupled equations to be
separated into two non-interacting parity blocks. Be-
cause the orientation of the SF z-axis is arbitrary, the
matrix elements (36.32) must be independent of M.
The rotational eigenfunctions of an asymmetric top,
such as water (H
2
O) or formaldehyde (H
2
CO), may
be written as linear combinations of the symmetric top
functions of (36.33):
| j
1
τm=
¯
k
j
1
¯
km η
j
1
¯
kmη
j
1
τm
, (36.34)
where the expansion coefficients
j
1
¯
km η
j
1
τm
are
labelled by − j
1
≤ τ ≤ j
1
. The parity (inversion sym-
metry) of these functions is η(−1)
j
1
+
¯
k
. Because protons
are fermions, the total (rotational and spin) nuclear wave
function must be antisymmetric under exchange of the
two protons in H
2
OorinH
2
CO. Proton exchange is
equivalent to a rotation through π about the symmetry
axis of the molecule. The rotational functions (36.34)
are eigenfunctions of this operator with eigenvalues
(−1)
¯
k
. As the ortho nuclear spin function is symmetric
under proton exchange, and the para function is anti-
symmetric, it follows that rotational states with
¯
k odd are
ortho states, whereas those with
¯
k even are para states.
Conservation of the parity η(−1)
j
1
+
¯
k
then implies that
η is either 1 or −1 in the summation on the right hand
side of (36.34). Thus, the index τ implies
¯
k = even or
¯
k = odd and η = 1orη =−1. The molecular internal
Hamiltonian matrix has four non-interacting diagonal
blocks, corresponding to the four possible combinations
of
¯
k and η [36.10, 11].
Recent studies of the rotational excitation of H
2
O
by H
2
[36.12, 13] show that, at low energies, the cross
sections can be much larger for collisions with ortho-H
2
( j
2
odd) than with para-H
2
( j
2
even). The long range
interaction between the (large) dipole moment of H
2
O
and the quadrupole moment of H
2
– absent for para-H
2
in
its ground state, j
2
= 0 – is responsible for this difference
in behavior.
References
36.1 R. B. Bernstein: Atom–Molecule Collision Theory
(Plenum, New York 1979)
36.2 J. M. Hutson, S. Green: MOLSCAT Computer Code
Version 12, distributed by CCP6 (UK Science, En-
gineering Research Council, Daresbury Laboratory
1993)
36.3 D. R. Flower, G. Bourhis, J.-M. Launay: Comput.
Phys. Comm. 131, 187 (2000)
36.4 A. S. Dickinson: Comput. Phys. Commun. 17,51
(1979)
36.5 A. Offer, D. R. Flower: J. Chem. Soc. Faraday Trans.
86, 1659 (1990)
36.6 C. Rist, M. H. Alexander, P. Valiron: J. Chem. Phys.
98, 4662 (1993)
36.7 A. R. Edmonds: Angular Momentum in Quantum
Mechanics (Princeton Univ. Press, Princeton 1974)
36.8 J. Schaefer, W. Meyer: J. Chem. Phys. 70,344
(1979)
36.9 D. R. Flower: Molecular Collisions in the Interstellar
Medium (Cambridge Univ. Press, Cambridge 1990)
36.10 B. J. Garrison, W. A. Lester, W. H. Miller: J. Chem.
Phys. 65, 2193 (1976)
36.11 T. R. Phillips, S. Maluendes, S. Green: J. Chem. Phys.
102, 6024 (1995)
36.12 M.-L. Dubernet, A. Grosjean: Astron. Astrophys.
390, 793 (2002)
36.13 A. Grosjean, M.-L. Dubernet, C. Ceccarelli: Astron.
Astrophys. 408, 1197 (2003)
Part C 36

561
Gas Phase Rea
37. Gas Phase Reactions
The rates of gas phase chemical processes can
generally be described by rate laws in which the
rate of formation of products or disappearance of
reactants is related to the product of the concen-
trations of reactants raised to various powers [37.1].
Rate laws are deterministic expressions that are
usually accurate even though they are used to rep-
resent a stochastic reality. Rate equations may fail
in the limit of small numbers of reacting particles,
where both fluctuations and discrete aspects are
important. Exceptions to the reliability of rate
equations have been found recently in a vari-
ety of fields including surface chemistry on small
particles [37.2]. Moreover, both Monte Carlo and
master equation methods can be used in their
place, given sufficient computing power [37.3–6].
37.1 Normal Bimolecular Reactions .............. 563
37.1.1 Capture Theories ....................... 563
37.1.2 Phase Space Theories ................. 565
37.1.3 Short-Range Barriers ................. 566
37.1.4 Complexes Followed
by Barriers ............................... 568
37.1.5 The Role of Tunneling ................ 569
37.2 Association Reactions........................... 570
37.2.1 Radiative Stabilization ............... 570
37.2.2 Complex Formation
and Dissociation ....................... 571
37.2.3 Competition with Exoergic
Channels.................................. 572
37.3 Concluding Remarks ............................ 572
References .................................................. 573
As an example of a rate law, consider the rate of dis-
appearance of reactant A in a gas mixture containing
species A, B,andC. The rate law for this disappearance
can be expressed by the equation
d[A]/ dt =−k[ A]
a
[B]
b
[C]
c
, (37.1)
where the symbols [ ] refer to concentration, and the rate
coefficient k is dependent on temperature, and possibly
other parameters such as the total gas density. The above
law is not the most general that can be envisaged. For
example, if species A reacts via more than one set of
processes, more than one negativeterm on the right-hand
side of the equation will be needed. In addition, if the
reverse reaction to form A from products is appreciable,
a positive term must also be included. At equilibrium,
the rate of change of reactant must be zero.
The relation above does not necessarily refer to one
chemical reaction, but to a succession of elementary
reactions known collectively as a mechanism. The most
elementary reaction is a simple bimolecular process with
a second order rate law of the type
d[C]/ dt =−d[A]/ dt = k[ A][B] ,
(37.2)
where two species A and B collide to form products,
one of which can be labeled C.Inthislaw,therate
coefficient k is related simply to the reaction cross
section σ via the equation
k = σv ,
(37.3)
where v is the relative velocity of reactants. The rate co-
efficient in a bimolecular process has units of volume per
time, typically cm
3
s
−1
. In a thermal system, the rate co-
efficient k(T ) is averaged over all degrees of freedom of
the reactants, both internal and translational. The most
specific rate coefficient is termed a state-to-state co-
efficient and refers to a process in which reactant A in
quantum state a reacts with reactant B in quantum state b
at a specific translational energy T to form products in
specific states separating with a specific translational
energy [37.7].
Although normal bimolecular processes produce
more than one product, it is also possible for the two
reactants A and B to stick together if sufficient energy
is released in the form of a photon:
A+ B −→ AB + hν.
(37.4)
Such a process is called radiative association [37.8],
and has mainly been studied for ion-molecule systems,
i. e., reactions in which one of the two reactants is an
Part C 37

562 Part C Molecules
ion. The process of radiative association is normally
thought to occur in two steps. The first step produces a
collision complex AB
∗
, which is a molecule existing in
a transitory fashion above its dissociation limit:
A+ B −→ AB
∗
. (37.5)
Once formed, the complex, which is often thought of
as an ergodic entity retaining memory only of its total
energy and angular momentum, can either redissociate
into reactants, or emit a photon of suffi cient energy to
stabilize itself:
AB
∗
−→ AB + hν. (37.6)
Since redissociation of the complex is generally more
rapid than radiative emission, radiative association rate
coefficients are normally small. Emission of one in-
frared photon is sufficient to achieve stabilization, but
stabilization of a complex via electronic emission may
be a more rapid mechanism if suitable electronic states
exist [37.8,9]. The lifetime of the complex against redis-
sociation into reactants is a strong direct function of the
binding energy of the species and the number of atoms
it possesses.
In addition to bimolecular processes, two other
types of reactions often referred to as elementary
are unimolecular and termolecular reactions. Although
complex reaction mechanisms are sometimes divided
into unimolecular and termolecular steps, these are not
strictly elementary because they can be subdivided into
a series of bimolecular steps. In a unimolecular reac-
tion [37.10,11], a molecule A is destroyed at sufficiently
high gas density by a process that has the seemingly
simple first order rate law
d[A]/ dt =−k[ A] .
(37.7)
At low pressures, on the other hand, the rate law is
second order. A simplified series of events, called the
Lindemann mechanism, explains these limiting cases
by invoking the activation of species A by strong in-
elastic collisions with bath gas M to form an activated
complex A
∗
which can either be deactivated by inelastic
collisions or spontaneously decompose, since it pos-
sesses sufficient energy to do so. The steps are written
as
A+ M
A
∗
+ M , (37.8)
A
∗
−→ B + C , (37.9)
where the spontaneous destruction of A
∗
can be thought
of as a truly elementary unimolecular reaction, akin to
spontaneous emission of radiation. Studies of sponta-
neous dissociation occupy an important place in gas
phase reaction theory, and are discussed in Sects. 37.1.2
and 37.1.4 in the context of dissociation of intermedi-
ate complexes. If the rate coefficients for the forward
and reverse processes in (37.8) are labeled k
1
and k
−1
respectively, and the rate coefficient for spontaneous
dissociation of A
∗
into products is labeled k
2
s
−1
,
application of the steady-state principle to the concen-
tration of the activated complex, namely,
d[A
∗
]/dt = k
1
[A][M]−k
−1
[A
∗
][M]−k
2
[A
∗
]≈0
(37.10)
leads to the rate law
− d[A]/ dt = k
[A][M] , (37.11)
where
k
= k
1
k
2
/
(
k
−1
[M]+k
2
)
.
(37.12)
At low pressures, k
−1
[M]k
2
and k
≈ k
1
so that
a second order rate law prevails. At high pressures,
k
−1
[M]k
2
and k
≈ k
1
k
2
/k
−1
[M] so that the rate law
becomes first order:
− d[ A]/dt ≈
(
k
1
/k
−1
)
k
2
[A] . (37.13)
Since both the activation and deactivation of complexes
occur stepwise, rather than in single strong collisions,
reality is far more complex than the Lindemann mech-
anism [37.12], and, at the highest degree of detail,
master equation treatments are needed, especially for
intermediate pressures [37.13].
In a termolecular reaction, which is actually the in-
verse of a unimolecular process [37.13], two species
B and C collide to form a collision complex A
∗
,which
can be regarded as the activated complex of stable
species A. The collision complex can be stabilized by
subsequent strong collisions with other species:
A
∗
+ M −→ A+ M , (37.14)
or can redissociate into reactants. If the complex forma-
tion step occurs with a bimolecular rate coefficient k
−2
,
and k
−1
and k
2
refer to complex stabilization and disso-
ciation as in the unimolecular case, the rate law for the
termolecular process can be written
d[A]/ dt = k
[B][C][M] , (37.15)
where
k
= k
−2
k
−1
/
(
k
−1
[M]+k
2
)
.
(37.16)
Part C 37

Gas Phase Reactions 37.1 Normal Bimolecular Reactions 563
At low pressures, k
≈ k
−2
k
−1
/k
2
and the rate law is
third order. At high pressures, when every activated
complex is deactivated, the rate law becomes second
order since k
≈ k
−2
/[M]. Actually, at very low pres-
sures radiative stabilization of the complex dominates
and the rate law once again becomes second order. As in
the unimolecular case, the complex does not really un-
dergo strong inelastic collisions, so that reality is once
again more complex than pictured here [37.13]. For
detailed theories of thermal reactions, there is the addi-
tional problem in (37.12)and(37.16) of deciding when
thermalization of the partial rate coefficients should be
undertaken. In reality, the partial rate coefficients refer
to reactions with specific amounts of energy and angu-
lar momentum, and should not be thermally averaged
before incorporation into the equations for k
.
37.1 Normal Bimolecular Reactions
The rates of elementary (bimolecular) chemical re-
actions are governed by Born–Oppenheimer potential
surfaces, which contain electronic energies and nuclear-
nuclear repulsions. Reactions can be classified as
exoergic or endoergic depending upon whether the 0 K
energies of the products lie below or above those of the
reactants, respectively. In the simplest types of exoergic
chemical reactions, the potential energy flows down-
hill from reactants to products, or flows downhill from
reactants to a global minimum (the reaction complex)
after which it flows uphill to products. More commonly,
the morphology of the potential surface is such that af-
ter some long-range attraction, the potential rises as old
chemical bonds are broken before falling as new bonds
are formed. Generally, there is a minimum energy path-
way through the region of large potential referred to as
the reaction coordinate. The system is said to traverse
a transition state barrier, which refers to the configura-
tion of atoms at which a potential saddle point occurs.
The height of this transition state barrier is related to the
activation energy barrier E
a
in the classical Arrhenius
rate law
k(T) = A(T ) exp
− E
a
/
k
B
T
, (37.17)
for rate coefficients of bimolecular reactions which
contain short-range barriers [37.1]. In the Arrhenius
expression, k
B
is the Boltzmann constant, and the pre-
exponential factor A(T) can be related to the form of
the long-range potential, or to an equilibrium coeffi-
cient between the transition state and reactants (see the
discussion of activated complex theory in Sect. 37.1.3).
Although fits of experimental data over short tempera-
ture ranges often assume the pre-exponential factor to
be totally independent of temperature, theories show that
this is not strictly true in most instances. A more seri-
ous problem with the expression undoubtedly occurs at
low temperatures since tunneling will clearly lead to
deviations.
Although, in principle, it is possible to calculate
reaction cross sections and rate coefficients via the
quantum theory of scattering, in practice few systems
have been studied by this technique given the immense
computational effort required [37.14, 15]. Another set
of approaches, which has been used to study a large
variety of systems, is known as classical molecular dy-
namics (see Chapt. 58). In these approaches, the atoms
move classically on the quantum mechanically gener-
ated Born–Oppenheimer potential surfaces. For many
reactions, however, neither technique is applicable, and
a variety of simpler approaches has been developed,
using capture and statistical approximations; these ap-
proaches will be emphasized here. Indeed, the use of an
ergodic complex in our preliminary discussion of associ-
ation and unimolecular reactions above presages the use
of statistical approximations. An excellent high-level re-
view article on many of the topics covered here has been
written by Troe [37.16].
37.1.1 Capture Theories
For reactions that do not possess a potential energy bar-
rier at short-range, it is tempting to apply long-range
capture theories between structureless particles to cal-
culate the reaction rate coefficient. Such theories assume
that (a) all hard collisions lead to reaction, and (b) hard
collisions occur for all partial waves up to a maximum
impact parameter b
max
or relative angular momentum
quantum number L
max
. This is normally defined so that
the reactant translational energy T
AB
is just sufficient
to overcome a centrifugal barrier. The centrifugal bar-
rier produces a long-range maximum in the effective
potential energy function V
eff
given by the relation
V
eff
(r, b) = V(r) + T
AB
b
2
/r
2
, (37.18)
where r is the separation between reactants and
T
AB
b
2
/r
2
is the angular kinetic energy. If the reactants
Part C 37.1

564 Part C Molecules
overcome the centrifugal barrier, they will spiral in to-
wards each other in the absence of short-range repulsive
forces. The approach has had its most notable success
for exoergic reactions between ions and nonpolar neu-
tral molecules [37.17]. The long-range potential in this
situation is simply (in cgs-esu units)
V(r) =−e
2
α
d
/2r
4
, (37.19)
where α
d
is the polarizability of the neutral reactant.
This potential leads to the Langevin rate coefficient
k = vπb
2
max
= 2πe(α
d
/µ)
1/2
, (37.20)
where µ is the reduced mass of the reactants. The the-
ory leads to a temperature-independent rate coefficient
with magnitude ≈ 10
−9
cm
3
s
−1
. Numerous experi-
ments from above room temperature to below 30 K
confirm its validity for the majority of ion–molecule re-
actions, which appear rarely to possess potential energy
surfaces with short-range barriers [37.18,19].
An analogous central force potential for structure-
less neutral–neutral reactants is the van der Waals or
Lennard–Jones attraction
V(r) =−C
6
/r
6
, (37.21)
where C
6
can be defined simply in terms of the
ionization potentials and polarizabilities of the reac-
tants [37.20,21]. The rate coefficient obtained using
a capture theory with this long-range potential is given,
after translational thermal averaging, by the equa-
tion [37.21]
k(T) = 8.56 C
1/3
6
µ
−1/2
(k
B
T)
1/6
, (37.22)
where all quantities are in cgs units. Equation (37.22)
leads to estimates for the rate coefficient at room tem-
perature in the range ≈10
−10
–10
−9
cm
3
s
−1
. Unlike
the situation for ion–molecule reactions, this estimate
has not received much attention mainly because most
neutral–neutral reactions involveactivationenergy. Even
for those systems without activation energy, the approx-
imation appears to lead to rate coefficients that are too
large by at least a factor of a few [37.21]. In place of the
result of (37.22), kineticists often use the simple hard-
sphere model with atomic dimensions for the reaction
cross section. The hard-sphere model leads to a tem-
perature dependence of T
1/2
, which is in disagreement
with a whole series of new experiments by Smith, Rowe,
and co-workers on fast neutral–neutral reactions down
to temperatures near 10 K [37.22].
Both long-range potentials considered above are
isotropic in nature. A variety of capture theo-
ries [37.23,24] have been developed which take angular
degrees of freedom into account. For ion–molecule sys-
tems in which the neutral species has a permanent dipole
moment µ
d
, the long-range potential becomes
V(r,θ)=−
e
2
α
d
2r
4
−
eµ
d
cos θ
r
2
, (37.23)
where θ is the angle between the radius vector from
the charged species to the center-of-mass of the dipolar
species and the dipole vector. Adiabatic effective (cen-
trifugal) potential energy curves can be defined at any
given fixed intermolecular separation r by diagonaliz-
ing angular kinetic energy and potential energy matrices
using a suitable basis set. If an atomic ion is reacting
with a linear neutral, a suitable basis set would con-
sist of spherical harmonics for the rotation of the linear
molecule (angular momentum j) as well as rotation ma-
trices for the relative motion (angular momentum L)
between the species. The eigenvalues of a matrix with
fixed total angular momentum J then correspond to the
effective radial potential energy functions V
eff
at each r.
The L, j labeling of the potential curves can be ascer-
tained by starting the calculation at sufficiently large r
so that L and j are reasonably good quantum num-
bers. Additional approximations, such as the centrifugal
sudden approximation, can be made to facilitate the cal-
culation [37.25]. Making the adiabatic assumption that
transitions between these potentials are not allowed at
long range, one obtains an adiabatic capture rate coeffi-
cient for each initial value of j and translational (radial
kinetic) energy T
AB
from the criterion
V
eff
( j, L
max
, R) = T
AB
, (37.24)
where R is the separation corresponding to the maxi-
mum effective potential. Unlike the Langevin approach,
the rate coefficients thermalized over translation for
each j show an inverse dependence on temperature,
with the j = 0 state showing the most severe depen-
dence since the dipole is essentially “locked” for this
state. Thermal averaging over j typically leads to rate
coefficients with an inverse dependence on temperature
between T
−1/2
and T
−1
[37.26]. Rate coefficients as
large as 10
−7
cm
3
s
−1
can be obtained as the temperature
approaches 10 K. Although most ion–dipole reactions
seem to obey capture theory models at low temperature,
there are exceptions.
An alternative approach to ion–dipole reactions us-
ing the classical concept of adiabatic invariants has been
developed [37.27]. In addition, variants to the capture
theory discussed here have been formulated. A statis-
Part C 37.1

Gas Phase Reactions 37.1 Normal Bimolecular Reactions 565
tical adiabatic approach has been developed [37.23],
in which adiabatic effective potential maxima are not
used to define capture cross sections, but to define rate
coefficients via the activated complex (transition state)
theory discussed in Sect. 37.1.3, which posits thermal
equilibrium between reactants and the species existing
at the potential maxima. One advantage of this sim-
plification is that it permits the adiabatic treatment to
be more easily extended to complex geometries, espe-
cially if perturbation approximations are utilized. Other
approaches involve the variational principle; an upper
bound to the capture rate coefficient can be determined
within the transition state, or bottleneck approach, which
defines the transition state through minimization of the
number of available vibrational/rotational states at the
bottleneck [37.28] (see Sect. 37.1.3).
Nonspherical capture theories have also been
used [37.29,30] to study rapid neutral–neutral reactions.
The role of atomic fine structure at low temperatures is
an especially interesting application; reactions involv-
ing atomic C and O with a variety of reactants have been
studied. Use of an electrostatic potential shows that the
reactivity of C or O atoms in their
3
P
0
states with dipo-
lar species is minimal. This is particularly important for
atomic carbon since at low temperatures it lies primarily
in its ground
3
P
0
state. The choice of an electrostatic po-
tential has been disputed [37.21] because experimental
results for C–hydrocarbon reactions at room tempera-
ture are best understood if the long-range potential
is dispersive (Lennard–Jones) in character rather than
electrostatic.
Reactions between radicals in
2
Π states (e.g. OH)
and
2
Σ states (e.g. CN) and stable molecules have also
been considered, especially at low temperature, with
long range potentials that contain both electrostatic and
dispersion terms. The results can be compared with new
low temperature experimental results on the CN
−
O
2
reaction, but the temperature dependence is not matched
by theory if the dispersion term is included [37.30,31].
In general, even the most recent capture theories are not
as reliable as those for ion–molecule systems [37.32].
Rapid neutral–neutral reactions can also be treated by
transition state theories (see below) [37.33] or, rarely, by
detailed quantum mechanical means [37.34].
The last five years have witnessed a burgeoning
interest in rapid neutral–neutral reactions at low tem-
perature studied with the so-called CRESU technique
(an acronym for Cinétique de Réaction en Ecoule-
ment Supersonique Uniforme) [37.22, 35–37]. The
new data should provoke new attempts at theoretical
understanding.
37.1.2 Phase Space Theories
Capture theories tell us neither the products of reaction,
if several sets of exoergic products are available, nor
the distributions of quantum states of the products. The
simplest approach to these questions for reactions with
barrierless potentials is to make a statistical approxima-
tion – all detailed outcomes being equally probable as
long as energy and angular momentum are conserved.
Such a result requires strong coupling at short range. The
most prominent treatment along these lines is referred
to as phase space theory [37.38]. In this theory, the cross
section σ for a reaction between two species A and B
with angular momentum quantum numbers J
A
and J
B
and in specific vibrational-electronic states colliding
with asymptotic translational kinetic energy T
AB
to form
products C and Din specific vibrational-electronic states
with angular momentum quantum numbers J
C
and J
D
is
σ(J
A
, J
B
→ J
C
, J
D
) =
π
2
2µT
AB
L
i
,J
(2L
i
+ 1)
× P(J
A
, J
B
, L
i
→ J)P
(J → J
C
, J
D
), (37.25)
where J is the total angular momentum of the combined
system, L
i
is the initial relative angular momentum
of reactants, P is the probability that the angular mo-
menta of the reactants add vectorially to form J, P
is
the probability that the combined system with angu-
lar momentum J dissociates into the particular final
state of C and D, µ is the reduced mass of reac-
tants, and the summation is over the allowable ranges
of initial relative angular momentum and total angu-
lar momentum quantum numbers. P
is equal to the
sum over the final relative angular momentum L
f
,of
angular momentum allowed (J → L
f
, J
C
, J
D
) com-
binations leading to the specific product state divided
by the sum of like combinations for all energetically
accessible product and reactant states. The ranges of
initial and final relative angular momenta are given
by appropriate capture models (e.g. Langevin, ion–
dipole, Lennard–Jones) as well as angular momentum
triangular rules. This procedure involves the implicit as-
sumption that strong coupling does not occur at long
range; rather, adiabatic effective potentials can be as-
sumed for initial and final states. The state-to-state rate
coefficient is simply the cross section multiplied by the
relative velocity of the two reactants. Summation over
all product states, as well as thermal averaging over the
reactant state distributions and the translational energy
distribution, can all be undertaken. Strategies for sum-
Part C 37.1
