Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

535

Molecular Pho

34. Molecular Photodissociation

Molecular photodissociation is the photoinitiated

fragmentation of a bound molecule [34.1]. The

purpose of this chapter is to outline the ways in

which molecular photodissociation is studied in

the gas phase [34.2]. The results are particularly

relevant to the investigation of the species involved

in combustion and atmospheric reactions [34.3].

34.1 Observables ........................................ 537

34.1.1 Scalar Properties ....................... 537

34.1.2 Vector Correlations .................... 537

34.2 Experimental Techniques ..................... 539

34.3 Theoretical Techniques ........................ 540

34.4 Concepts in Dissociation ....................... 541

34.4.1 Direct Dissociation..................... 541

34.4.2 Vibrational Predissociation ......... 542

34.4.3 Electronic Predissociation........... 542

34.5 Recent Developments........................... 543

34.6 Summary ............................................ 544

References .................................................. 545

Conceptually the photodissociation process can be di-

vided into three stages. During the ﬁrst stage the

molecule absorbs a photon and is promoted to an excited

state. This is generally an excited electronic state, but can

be a highly excited vibrational state in the ground elec-

tronic state. In the second stage, the transient complex

evolves through a series of transition states, until ﬁnally,

in the third stage, the molecule enters the exit channel

and dissociates into the products. Schematically, this

might be represented, for a triatomic molecule ABC

(see Fig. 34.1), as

ABC +

ω → (ABC)

‡

→ AB(v, j ) + C . (34.1)

In the case of the triatomic molecule represented here,

the dissociation involves the transformation of one of

the vibrational modes to a translational, or dissocia-

tive, mode, another vibrational mode (the bending) to

rotational motion of the products ( j), whilst the third

vibrational mode is preserved (v).

When the molecule is promoted to an electronic state

which has a purely repulsive potential energy surface

(PES), it undergoes very rapid dissociation, often in

less than one vibrational period. This is called direct

dissociation. However, the dissociation of the transient

complex can be delayed, taking place over many vi-

brational periods. This is called indirect dissociation,or

predissociation, and has been divided into three different

categories [34.4], though as with the division between di-

rect and indirect, this is sometimes somewhat arbitrary.

Vibrational Predissociation (Herzberg Type II)

In this case, the transient complex is on a vibrationally

adiabatic potential energy surface (this is an effective

potential for the molecule when it is in a particular vi-

brational state v) which is not dissociative, or which has

a barrier to dissociation. Therefore, to dissociate it must

either tunnel through the barrier, which is the only pos-

sibility for v = 0, or undergo a nonadiabatic transition

to a lower vibrational state, thereby transferring energy

from a vibrational degree of freedom to the dissociative

mode. This process of energy exchange is commonly

called the intramolecular redistribution of vibrational

energy (IVR).

Rotational Predissociation (Herzberg Type III)

In this case, the transient complex is on a nondisso-

ciative rotationally adiabatic potential energy surface.

Therefore, in a similar manner to vibrational pre-

dissociation, if it is to dissociate it must undergo

a nonadiabatic transition to a lower rotational state,

thereby transferring energy from rotation to the disso-

ciative mode.

Electronic Predissociation (Herzberg Type I)

In this case, the PES of the electronic state of the

transient complex is not dissociative at the given en-

ergy, and in order to dissociate the molecule must

undergo a nonadiabatic transition to a second disso-

ciative electronic state. This involves the coupling of

nuclear and electronic motion and therefore leads to

Part C 34

536 Part C Molecules

P[AB(A,α)]

P[AB(X,α)]

σ (ω)

ABC(B

)

t⬘ =0

t⬘⬎0

ABC(A

)

t =0

t ⬎ 0

ABC(X

)

AB(A,α)+C

AB(X,α)+C

Dissociation coordinate R

˜–

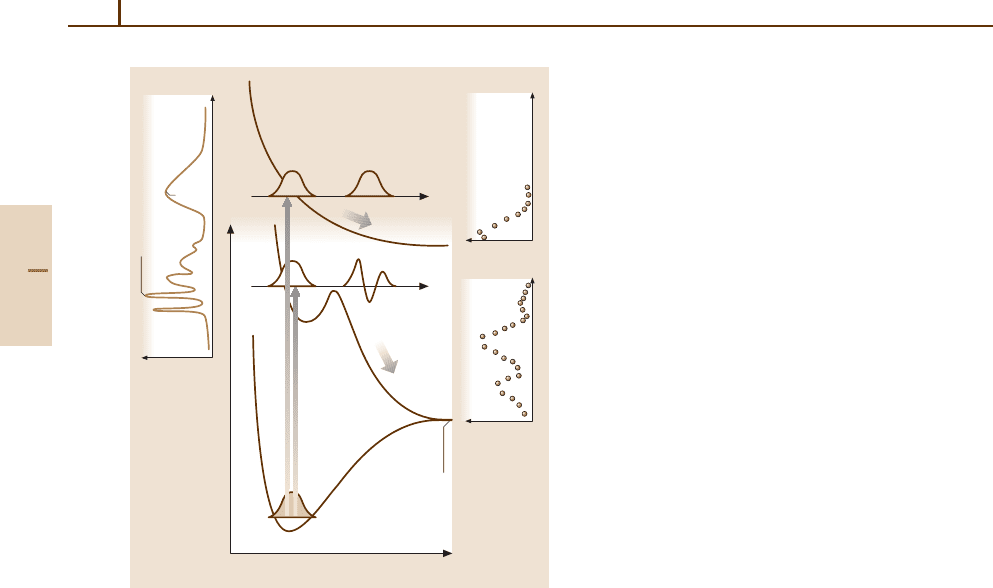
Fig. 34.1 Schematic representation of the uv photodis-

sociation of a triatomic molecule ABC into products

AB(α) and C, illustrating the total absorption cross

section σ(ω), evolution of the molecular wavepacket,

and asymptotic product state distributions P(α), for di-

rect and indirect dissociations on

B and

A state PESs

respectively

a break down of the Born–Oppenheimer (BO)ap-

proximation. There are two main types of electronic

predissociation. In the ﬁrst case, there is only a very

small coupling, and no actual crossing, between two

different electronic states, and the transition between

the two is driven by the very high density of vi-

brational states on the second electronic state. This

is called internal conversion for spin-allowed pro-

cesses, and intersystem crossing for spin-forbidden

processes. In the second case, the transition between

the electronic states is driven by strong coupling. This

coupling can be vibronic (vibrational-electronic) in

nature, e.g., for the Renner–Teller and Jahn–Teller ef-

fects, or purely electronic, as in the case of a conical

intersection.

Selection Rules

Two sets of selection rules apply to photodissocia-

tion. The ﬁrst set governs the allowed states to which

the molecule can be promoted by the photon. These

selection rules are simply those for bound-state spec-

troscopy (Sect. 33.4). Note in particular the selection

rule ∆ J = 0, ±1. This has important practical impli-

cations since it means that a molecule which is initially

rotationally cold remains so after absorption of a photon.

Thus, those observables which are averaged over J will

have a clear structure experimentally, and will be easier

to calculate theoretically. This is in contrast to scatter-

ing experiments which in general involve a summation

over many J states (Chapt. 36).

The second set of selection rules governs the disso-

ciation process. The transient complex, or prepared ( p)

state, will undergo transitions to a ﬁnal ( f ) vibrational,

rotational or electronic state in order to dissociate; these

transitions have their own set of selection rules. As for all

selection rules, these are determined on the basis of sym-

metry. For a total wave function Ψ and a perturbation

function W, which consists of the coupling terms or ne-

glected terms in the Hamiltonian,



∗

WΨ

dτ must be

nonzero for a transition to take place. As W forms a part

of the Hamiltonian, it is totally symmetric, and there-

fore the integral is nonzero only if the prepared and ﬁnal

state irreducible representations are equal, Γ

= Γ

.If

there is a transition to an excited electronic state, the

point groups of the initial and ﬁnal states are often not

the same, in which case the point group formed by the

joint elements of symmetry is used, or, in the case where

there is no stable geometry for one of the states, the sym-

metry of the potential is used. For a diatomic molecule

these selection rules are given in Table 49.2.

If the motion can be separated into vibrational, ro-

tational, and electronic parts, so that Ψ = Ψ

and

W = W

+ W

, it is then possible to derive three

separate selection rules: Γ

= Γ

for the rotational mo-

tion, i. e. conservation of internal angular momentum;

= Γ

for the electronic motion; and Γ

= Γ

for

the vibrational motion. Since the ﬁnal vibrational state

is in the continuum, in practice all vibrational species

(Γ

) are available at a given energy, so that the vi-

brational selection rule is not signiﬁcantly restrictive.

This separation is not possible in the case of electronic

predissociation occurring through the Renner–Teller or

Jahn–Teller effect, where it is necessary to consider the

vibronic species of the initial and ﬁnal states.

Part C 34

Molecular Photodissociation 34.1 Observables 537

34.1 Observables

Fundamental to any study of photodissociation is the

measurement or calculation of the characteristic prop-

erties, or observables, of the reaction, from which the

underlying dynamics of the fragmentation process can

be inferred.

34.1.1 Scalar Properties

The absorption cross section σ(ω) is a measure of the ca-

pacity of the molecule to absorb photons with frequency

ω. It is analogous to the line intensity in bound-state

spectroscopy. Assuming that the light-matter interac-

tion is weak (Chapt. 68), and that the light pulse is on

for a long time, the absorption cross section is given by

σ(ω) ∝ ω







E·







, (34.2)

where Ψ

and Ψ

represent the initial and ﬁnal states,

whose energies differ by

; E is a unit vector in the

direction of the polarization of the electric ﬁeld, and

µ is the electric dipole operator of the molecule. As-

suming the Born–Oppenheimer separation of electronic

and nuclear motion, (34.2) can be rewritten as

σ(ω) ∝ ω











, (34.3)

where the electronic transition dipole moment µ

equals Ψ

|E·

µ|Ψ

, and is in general dependent on the

internal coordinates of the molecule. The superscripts

(r, v) will be dropped from now on, and Ψ will refer

to the wave function for the internal coordinates of the

molecule.

The absorption cross section reﬂects not only the

nature of the transient complex but also its evolution

through the transition states. For direct dissociation the

absorption cross section is usually very broad and struc-

tureless. In contrast, the absorption cross section for

predissociation is structured, containing lines which are

normally Lorentzian in shape, and whose widths Γ are

related to the lifetime of the transient complex at that

energy by τ =

/Γ .

The partial photodissociation cross sections σ(ω, α)

are a measure of the capacity of the molecule to ab-

sorb photons with frequency ω and to yield products in

quantum state α. They are deﬁned by

σ(ω, α) ∝ ω











, (34.4)

where Ψ

is the ﬁnal wave function for the products

in the quantum state α. The partial cross sections for

direct dissociation are broad and featureless. For predis-

sociation, similar structures are seen in the partial cross

sections as in the absorption cross section. The absorp-

tion or total cross section is given by the sum of the

partial cross sections over all ﬁnal product states:

σ(ω) =



σ(ω, α) . (34.5)

The rotational and vibrational product distributions

P(ω, α) provide information about the amount of prod-

uct formed by a photon with frequency ω in a particular

rotational or vibrational state α. These are related to the

partial cross sections by P(ω, α) = σ(ω, α)/σ(ω).The

rotational and vibrational product distributions reﬂect

the nature of the transient complex as it enters the exit

channel, as well as the dynamics in the exit channel.

The branching ratios for different chemical species

produced in photodissociation are deﬁned as the fraction

of the total number of parent molecules that produce the

particular species of interest. In (34.1), the molecule

ABC dissociated into AB + C. It might equally well

have dissociated to A + BC, or indeed A + B + C. It

is clear then that there may be several different reaction

schemes, or channels, for the photodissociation of one

particular molecule. Thus, the branching ratio for form-

ing AB is the yield of this ﬁrst channel divided by the

total dissociation yield into all possible channels. Fur-

ther, it would sometimes be possible to produce AB, or

any of the other chemical species, in various electronic,

vibrational or/and rotational quantum states. In this case,

the branching ratio for forming AB(α) is the yield of AB

in the speciﬁc quantum state α divided by the total yield

of AB; however, this describes the branching into only

this particular reaction channel.

For the reaction scheme represented in (34.1), the

quantum yields of the products AB and C are the same.

However, for example, in the reaction

ABC

+ ω → (ABC

)

‡

→ AB(v, j ) + 2C ,

(34.6)

the quantum yield of C is twice that for AB. In gen-

eral, the quantum yield of a particular product fragment

for one reaction channel is the ratio of the number of

fragments formed to the number of photons absorbed.

However, it is again possible for a molecule to dissociate

into various different reaction channels. In such a case,

to obtain the overall quantum yield for a particular prod-

uct, the quantum yield for each reaction channel must be

summed over all the available reaction channels, taking

into account the branching ratios for the channels.

Part C 34.1

538 Part C Molecules

34.1.2 Vector Correlations

Photodissociation is by its very nature an anisotropic

process, as can be seen from (34.2). The operator

µ de-

ﬁnes a speciﬁc axis in the molecular body-ﬁxed frame

of reference. At the instant of photoexcitation,

µ is

preferentially aligned parallel to the polarization of

the electric ﬁeld E in the external laboratory space-

ﬁxed frame of reference. Hence, E deﬁnes a speciﬁc

axis, and thus cylindrical symmetry in the body-ﬁxed

frame. If fragmentation occurs on a time scale which

is short compared with overall rotation of the excited

complex, this correlation persists between the body-

ﬁxed frame and the space-ﬁxed frame, and a wealth

of information can be obtained. However, rotation of

the transient complex prior to fragmentation serves

to degrade this symmetry in the external body-ﬁxed

frame.

Three vectors fully describe the photodissociation

process for both the parent molecule and the prod-

ucts: (i)

µ in the body-ﬁxed frame (and hence E,in

the space-ﬁxed frame, at the instant of photoexcita-

tion); (ii) v, the recoil velocity of the products; and

(iii) j, the rotational angular momenta of the frag-

ments. Vector correlations can exist between all of these

vectors [34.5].

The most commonly observed is the angular distri-

bution of the photofragments I(θ, α), i. e. the relation

I(θ, α) ∝

4π



1 + β(α) P

(cos θ)



(34.7)

between v and E. P

(x) is the second-order Legen-

dre polynomial and θ is the angle between v and E.

The anisotropy parameter β(α) ranges between −1

for a perpendicular transition and +2 for a paral-

lel transition. Thus, measuring the angular distribution

of the fragments provides information about the type

of electronic transition and hence the electronic sym-

metry of the excited state [34.6]. If the alignment

between the body-ﬁxed and space-ﬁxed frames is de-

stroyed, the angular distribution becomes isotropic and

β(α) = 0. The anisotropy parameter depends on the

product channel α.

A second vector correlation concerns the direc-

tion of j with respect to E. Fragmentation generates

rotational motion in the nuclear plane: for a perpen-

dicular transition this is perpendicular to the plane

containing the atoms, leading to the projection of j

being preferentially aligned parallel to

µ, and thus

E in the space-ﬁxed frame. For a parallel transition,

the opposite would be true, i. e. j would be aligned

Fig. 34.2 Spatial recoil anisotropies and Doppler line shape

proﬁles, for parallel and perpendicular transitions compared

with an isotropic distribution

in the plane perpendicular to

µ. The alignment of

j leads to polarized emission/absorption depending

on whether molecules are created in an electroni-

cally excited/ground state. Therefore the orientation

of the product polarization with respect to the origi-

nal photolysis polarization E also yields information

about the symmetry of the electronic states involved in

dissociation.

The ﬁnal association in this series is independent of

the space-ﬁxed frame, since v and j are both deﬁned

in the body-ﬁxed frame. Unlike the two previous corre-

lations, a long lifetime does not destroy the alignment,

as it is not established until the bond breaks and the

two fragments recoil. For a tetratomic (or larger) mol-

ecule there are, in principle, two possible sources of

product rotational excitation: bending motion in a plane

of the molecule producing fragments with v perpen-

dicular to j; or torsional motion leading to fragment

rotation out of the plane. A prime example of this is the

distinction between frisbee and propeller type motion

of the two OH fragments in the dissociation of hydro-

gen peroxide [34.7, 8]. Measurement of only the scalar

properties cannot discriminate between these two pos-

sibilities, highlighting the additional information that

can be gained about the bond rupture and the exit

channel dynamics by the study of vector correlations

(Fig. 34.2).

Part C 34.1

Molecular Photodissociation 34.2 Experimental Techniques 539

34.2 Experimental Techniques

Early photochemical experiments used broad white-

light continuum sources and large diffractome-

ters [34.4]. However, it has been the development of

lasers in combination with molecular-beam techniques

that has dramatically increased the understanding of

photodissociation processes. The ever increasing spec-

tral and time resolutions of lasers, in addition to the

power and range of wavelengths available, have made

it possible to excite molecules selectively and with high

efﬁciency. This has enabled state-speciﬁc preparation of

the parent molecule, study of time evolution, as well as

the measurement of the scalar and vector properties of

the asymptotic products [34.9].

Speciﬁcation of the Initial State

A room temperature sample of a gas will have a Boltz-

mann distribution over rotational states. Molecular beam

techniques provide an improved speciﬁcation of the

initial angular momenta in the parent molecule by isen-

tropically cooling its internal rotational energy [34.10].

Full quantum state speciﬁcation can be achieved by

various two-photon excitation schemes, e.g., stimulated

emission pump (SEP) spectroscopy and vibrationally

mediated dissociation. SEP is commonly used to study

dissociation on the ground state PES; the molecules

are excited to a stable upper electronic state, stim-

ulated emission back to the ground state prepares

a single quasibound state. Vibrationally mediated dis-

sociation provides information about both ground and

upper electronic states; the molecules are excited to

a stable intermediate vibrational level on the ground

state and further excitation promotes this fully de-

ﬁned wave function to an upper dissociative electronic

state [34.11].

Detailed Measurement

of the Absorption Cross Section

UV and VUV electronic spectroscopy has proven a very

powerful tool for examining the interaction of a pho-

ton with a parent molecule (Chapt. 69). Absorption

cross sections are typically measured by scanning

the frequency domain and monitoring either the in-

tensity of radiation absorbed or the ﬂux of product

molecules produced. State speciﬁc detection of the

product ﬂux yields the partial cross section σ(ω, α).

Explicit measurement of σ(ω) is a direct applica-

tion of the Beer–Lambert law (Sect. 69.1) and thus

depends on the length of the optical cavity: cavity

ring-down spectroscopy with multiple passes through

a cell provides an effective cell length of several tens of

kilometers.

Evolution of the Transient Complex

The evolution of the molecular wavepacket can be

probed by time-resolved spectroscopy, as discussed

in Chapt. 35 and [34.12]. Real-time analysis of the mo-

lecular wavepacket provides a direct insight into the

forces acting during molecular photodissociation. This

type of time-resolved spectroscopy and the energy-

resolved spectroscopy described above are mutually

exclusive due to the time-energy uncertainty principle

(Sect. 80.3.1).

Asymptotic Properties

The vast majority of photodissociation studies determine

asymptotic properties of the dissociation process, meas-

uring either internal energy, recoil velocity, or angular

distributions of the dissociation products. The prod-

uct state distributions are usually explicitly probed by

laser-induced ﬂuorescence (LIF), resonance-enhanced

multiphoton ionization (REMPI) spectroscopy, or co-

herent Raman scattering with the relative populations of

the products obtained via line intensities.

The distribution and anisotropy of the recoil ve-

locities are measured using Doppler spectroscopy or

time-of-ﬂight (TOF) techniques [34.13]. Doppler spec-

troscopy uses the Doppler-broadening of lines in the

LIF or REMPI excitation spectra (Sect. 69.5); the pro-

ﬁle of the line shape also depends on the recoil

anisotropy of the probed species (Fig. 34.2). How-

ever, many important molecular fragments are not

amenable to spectroscopic detection. Thus, though

lacking the ultimate state-speciﬁcity of spectroscopy,

TOF techniques by virtue of their general appli-

cability provide an appealing alternative route to

determine the product state distributions. In TOF

techniques, the time is recorded for photofragments

to recoil a known distance from the interaction

region to a detector. Due to total energy and

momentum conservation, the translational energy dis-

tribution of a fragment state speciﬁcally detected

directly implies the internal energy distribution of

the other partner product. In less favorable cases

where this is not possible, coincidence detection

schemes are employed to deﬁne the partition be-

tween translational and internal energies. Rotation of

the detection axis with respect to the polarization

of the photolysis laser yields the recoil anisotropy.

Part C 34.2

540 Part C Molecules

Advances in spatially resolved detection schemes

are now providing an improved measure of vector

correlations.

Mass spectrometry can be used to measure branching

ratios and quantum yields, which can also be obtained

from the techniques described above.

34.3 Theoretical Techniques

The calculation of the observables of photodissociation

can be carried out using quantum mechanics either in

the time-independent or the time-dependent frame, as

well as using classical mechanics [34.1]. Theoretical

studies have contributed greatly to the understanding of

photodissociation processes, as they provide the ability

not only to calculate the observables, but also, through

the knowledge of the wave function, to view directly the

dissociation dynamics. This has enabled the inference

of the underlying dynamics from the observables of the

reaction to be more precisely established.

Due to computer limitations, the majority of quan-

tum mechanical studies currently treat fully only three

degrees of freedom, and thus have mainly concentrated

on triatomic molecules. Jacobi coordinates are usually

used, with the appropriate set for the dissociation of

ABC into AB and C as follows: R, denoting the dis-

tance between the atom C and the centre of mass of the

AB fragment; r, denoting the internal vibration coordi-

nate of AB; and γ , denoting the bending angle between

R and r.

The initial state Ψ

is generally taken to be a single

bound state. It is obtained either by the solution of the

Schrödinger equation at a particular energy (Sect. 31.4),

or simply by taking a product of three Gaussians in the

three coordinates, with the parameters of the Gaussians

being determined from spectroscopic information on the

ground state.

Further, to calculate the observables it is also nec-

essary to have information about µ

.However,this

is often assumed to be a constant, i. e. independent of

the internal coordinates of the molecule. The Franck–

Condon principle assumes that the nuclear geometry

changes after the electronic transition, and not during

it. Therefore a molecule, with a particular geometry,

will, when promoted by the photon to the excited elec-

tronic state, be centred around the same geometry,

which is thus referred to as the Franck–Condon region,

or point.

To carry out any dynamical calculations it is nec-

essary to have PESs for the electronic states involved.

These are usually obtained from ab initio calculations

which are described in Chapt. 31. The accuracy of the

PES surface largely determines the accuracy of the re-

sults obtained, as the PES essentially determines the

dynamics of the fragmentation process.

In the time-independent approach, a solution of the

time-independent Schrödinger equation



H− E



= 0 , (34.8)

is sought for a speciﬁc total energy E subject to appro-

priate boundary conditions at inﬁnite product separation.

There are many different approaches to solving this

problem, but they can be broadly separated into two

groups: scattering methods and L

methods. The scatter-

ing methods involve the solution of the coupled channel

equations described in Chapt. 36. These can be solved

directly to yield the wave functions, which can then be

used to calculate the observables, or can be solved in-

directly to provide similar information. The use of L

methods, which attempt to expand Ψ in a ﬁnite basis set,

is not directly applicable since the wave functions are

in the continuum and spread out to inﬁnite distances in

the R coordinate. Thus various modiﬁcations have been

introduced in order to take this into account. The most

important of these use variational principles [34.14],

such as that due to Kohn [34.15]. In the Kohn variational

principle the wave function in the inner or interaction re-

gion is expanded in a ﬁnite L

basis. However, in the

outer region, the wave function is expanded in an en-

ergy dependent basis of outgoing and incoming waves,

which are approximate solutions of the coupled channel

equations. Other methods which can sometimes be used

to indirectly extract information about the observables

are stabilization [34.16] and complex scaling [34.17].

In the time-dependent approach [34.18], one solves

the time-dependent Schrödinger equation

∂

∂t

Φ(t) =

HΦ(t)

(34.9)

for the wavepacket Φ(t) with initial condition

Φ(0) = Ψ

, i. e. it is assumed that the molecule is ver-

tically promoted by an inﬁnitely short pulse to the

electronic state under consideration. The wavepacket

is a coherent superposition of stationary wave func-

tions Ψ

(Chapt. 35), and since it comprises many of

the stationary states, it contains all the information

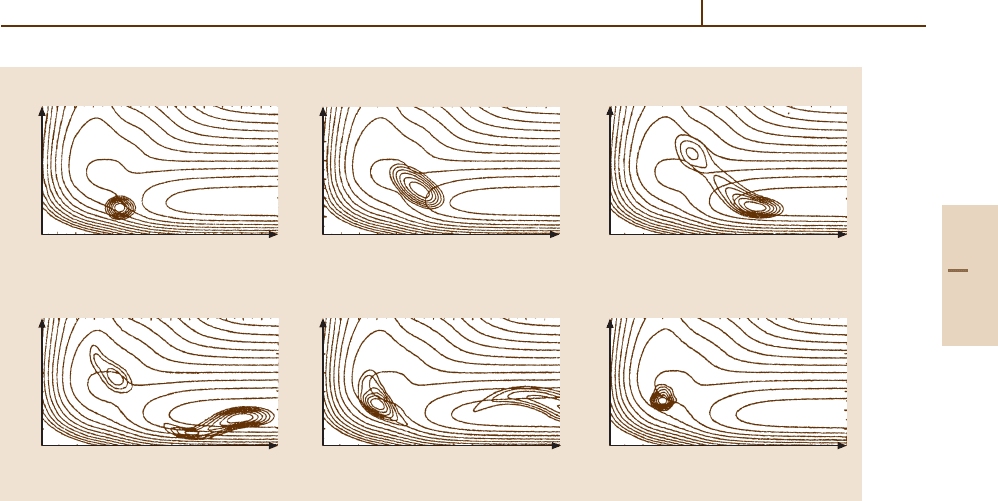
necessary to characterize the dissociation (see Fig. 34.3).

Part C 34.3

Molecular Photodissociation 34.4 Concepts in Dissociation 541

3.0

2.6

2.2

1.8

2.5 2.9 3.3 3.7 4.1 4.5 4.9 2.5 2.9 3.3 3.7 4.1 4.5 4.9 2.5 2.9 3.3 3.7 4.1 4.5 4.9

2.5 2.9 3.3 3.7 4.1 4.5 4.9

3.0

2.6

2.2

1.8

2.5 2.9 3.3 3.7 4.1 4.5 4.9 2.5 2.9 3.3 3.7 4.1 4.5 4.9

3.0

2.6

2.2

1.8

3.0

2.6

2.2

1.8

3.0

2.6

2.2

1.8

3.0

2.6

2.2

1.8

d) e) f)

a) b) c)

r(a

) r(a

)

r(a

) r(a

)

R(a

) R(a

)

R(a

) R(a

)

Fig. 34.3 Time evolution of a wavepacket in the dissociation of FNO in the S

state

The total absorption cross section is given by

σ(ω) ∝

+∞



−∞

dtS(t) e

−iωt

, (34.10)

where the autocorrelation function S(t) is deﬁned as

S(t) =Φ(0) | Φ(t) .

(34.11)

The autocorrelation function reﬂects the motion of the

wavepacket, and therefore is a convenient means for

visualizing the molecular dynamics. The individual par-

tial cross sections can be obtained in the limit t →∞

by projection of the wavepacket onto the stationary

wave functions of the products, i. e. plane waves in the

dissociation coordinate and vibrational-rotational wave

functions for the free products.

34.4 Concepts in Dissociation

There has been substantial experimental and theoretical

work to elucidate the processes involved in photodisso-

ciation from knowledge of the observables, and much

progress has been made. In this section, an attempt is

made to present some of the simpler ideas which have

emerged [34.1].

34.4.1 Direct Dissociation

Direct dissociation is the very fast rupture of a bond af-

ter a molecule has been promoted to an electronic state

which has a purely repulsive PES. A very clear picture

of this process can be obtained from wavepacket calcu-

lations: the wavepacket which is placed on the repulsive

surface moves directly down the PES and into the exit

channel. The autocorrelation function decays from one

to zero in a short time and does not show any recur-

rences, i. e. oscillations in the autocorrelation function.

The absorption cross section σ(ω), which is the Fourier

transform of the autocorrelation function (34.10), is

therefore a very broad Gaussian with no structure. The

breadth of σ(ω) is inversely proportional to the width of

the autocorrelation function and can, using simple clas-

sical pictures, be taken to be approximately proportional

to the steepness of the potential at the Franck–Condon

point. The partial cross sections have a similar struc-

ture to the total cross section, though they have differing

intensities and are shifted relative to each other on the

energy scale.

The product distributions can be predicted using

simple classical pictures. These methods can be di-

vided into two groups, depending on the extent of the

Part C 34.4

542 Part C Molecules

excitation/de-excitation, or coupling, in the exit chan-

nel. If there is very little excitation/de-excitation in

the exit channel, the rotational and vibrational product

distributions are best described using Franck–Condon

mapping. Another model which gives good results for

the rotational distributions is the impact parameter, or

impulsive, model. If excitation/de-excitation in the exit

channel is not negligible, the product distributions are

best described using the reﬂection principle.Thisre-

lates the distribution of the initial wavepacket in γ to

the ﬁnal rotational distributions through the classical

excitation function. Similarly, the distribution of the

initial wavepacket in space is related to the ﬁnal vibra-

tional distributions through another classical excitation

function.

Even for a purely repulsive PES, the potential may

be very ﬂat in the Franck–Condon region so that the

molecule may be able to undergo one internal vibra-

tion before it dissociates. In this case, there is a diffuse

structure in σ(ω), associated with recurrences in the

autocorrelation function. The spacing of the structures

in σ(ω) are related to the period of the internal vibra-

tions by ∆ E = 2π

/T . Diffuse structures in σ(ω) have

also been linked to unstable periodic orbits.

34.4.2 Vibrational Predissociation

Vibrational predissociation is dissociation delayed due

to the trapping of the energy of the molecule in modes

orthogonal to the dissociation coordinate. It can be ex-

plained very clearly in the time-independent picture as

resonances (sometimes known as Feshbach resonances),

which are simply extensions of the bound states into

the continuum. σ(ω) in this case consists of a series of

Lorentzian lines, whose width is inversely proportional

to the lifetime of the resonance. In the case where the

internal modes of the molecule are not strongly coupled

to each other or to the dissociation mode, these reso-

nance states can often be assigned, with the number of

quanta in each mode being speciﬁed. In this case, the

lines in σ(ω) form a series of progressions. The widths

of these lines, and thus the lifetimes of the resonance

states, often show trends relating the lifetimes to the as-

signment. This is called mode-speciﬁcity. In the case

that the system is strongly mixed, it is not possible to

make an assignment of the resonances, and the life-

times show strong ﬂuctuations. This is called statistical

state-speciﬁcity [34.19].

The resonances can also be seen in the time-

dependent picture, where the autocorrelation function

shows many recurrences with periods T , depending

on the fundamental frequencies of the internal modes

ω = 2π/T (Chapt. 35).

The partial cross sections for vibrational predissoci-

ation also consist of Lorentzian lines, with positions and

widths exactly as for the total cross sections, but with

differing intensities. The partial widths, which describe

the rate of dissociation into each product channel, are

given by

= Γ

σ(ω, α)

tot

(ω)

(34.12)

In the weak coupling case, simple pictures can be

used to describe the product distributions. The rotational

product distributions can be explained using again the

reﬂection principle; but in this case, instead of consider-

ing the distribution of the initial wave function in γ ,the

distribution of the wave function at the transition state

is used. The vibrational product distributions can often

be well described by examining vibrationally adiabatic

curves.

In the case that the modes are strongly coupled, the

simple models break down. It is then sometimes pos-

sible to use statistical models to describe both the rates

and the product distributions. One example of these

unimolecular-statistical theories is the Ramsperger–

Rice–Karplus–Marcus (RRKM) theory, which is widely

used for the description of unimolecular dissocia-

tions [34.20]. Another example is phase space theory

(PST) [34.21, 22] which is often used to calculate the

product distributions for reactions which have no bar-

rier. The quantum mechanical results ﬂuctuate about

these average values. These ﬂuctuations, which can be

considered as being independent of the system, can be

described well by the predications of random matrix

theory [34.23].

34.4.3 Electronic Predissociation

Nonadiabatic transitions between two or more electronic

states are a common phenomenon in photodissocia-

tion [34.24] as well as in other chemical reactions

(Chapt. 49). Such transitions can result in the produc-

tion of both electronically excited and ground state

fragments.

Adiabatic molecular PESs can vary in complex fash-

ions. Many of these contortions arise from avoided

and real crossings of the surfaces, and in all such

cases, the physical and chemical understanding is

greatly facilitated by expressing the adiabats in terms

of the diabatic states (Chapt. 31).Theelectronicdi-

abatic states are chosen to simplify the structure of

Part C 34.4

Molecular Photodissociation 34.5 Recent Developments 543

the electronic wave functions by incorporating the off-

diagonal or coupling elements as a pure potential energy

term, rather than as a kinetic term, or a mixture of

both.

Under these conditions, the BO approximation is in-

adequate since there is coupling between the different

adiabatic states, and the electronic and nuclear motion

cannot be separated. Therefore the solution of the time-

dependent Schrödinger equation (Sect. 34.3) requires

the set of coupled equations

∂

∂t







+ T





(34.13)

to be propagated, where the coupling between the dia-

batic surfaces is in the potential (V ) and not the kinetic

(T ) terms. The wavepacket evolves on both diabatic (or

adiabatic) surfaces, and shows a complicated motion in

moving between the two surfaces. The coupling between

the nuclear and electronic motion can be thought of as

resulting in the nuclear motion forcing the transfer of

a valence electron to another molecular orbital. Since

the efﬁciency of this transfer is greatest when the or-

bitals are degenerate, the crossings of the wavepacket

between the PESs are generally localized around their

degeneracies. Finally, the wavepacket moves out on the

adiabatic surfaces towards the products, with which they

are correlated.

34.5 Recent Developments

In recent years, the ﬁeld of photodissociation has seen

a number of intriguing applications and comparisons

between detailed experimental data and high-quality

ab initio calculations. These applications have become

feasible mainly because of the possibility to construct

accurate potential energy surfaces from ﬁrst principle

electronic structure calculations. Cases in which the

fragmentation proceeds via two or several electronic

states have been especially concentrated on [34.26]. In

these cases the Born–Oppenheimer approximation is not

valid and the coupling between electronic and nuclear

degrees of freedom is essential (Sect. 34.4.3). A nice

example is the photodissociation of water in the sec-

ond absorption band. Since water has only 10 electrons,

highly accurate potential energy surfaces have been

calculated theoretically, and these have been used in

extensive dynamics calculations – including motion on

three potential energy surfaces [34.27]. The agreement

between the calculated and the measured absorption

cross section at room temperature is outstanding [34.28].

From the elaborate analysis of product state distributions

(rotational, vibrational, and electronic), many details

about the coupled motion on several potential energy

surfaces have been learned [34.29, 30]. The electronic

density of water is small, and therefore the photodisso-

ciation can be treated on a nearly exact level. For other

triatomic molecules, with more electrons and a higher

density of electronic states, this is generally not fea-

sible. An important example is ozone, which plays

a vital role in the atmosphere. The electronic structure of

is illustrated in Fig. 34.4, where many spin-allowed

as well as spin-forbidden fragmentation pathways are

Potential energy (eV)

)

2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0

Potential energy (eV)

)

2.0 2.5 3.0 3.5 4.0 4.5 5.0 5.5 6.0

A''

Fig. 34.4 Electronic structure of ozone. Shown are cuts

through the potential energy surfaces for the singlet and

triplet states. After [34.25]

Part C 34.5

544 Part C Molecules

0 1000 2000 3000 4000

k(E

†

)(s

–1

)

†

(cm

–1

)

Fig. 34.5 Overview of the calculated dissociation rates of HOCl as

a function of the excess energy. The solid line is the prediction of

a statistical model. After [34.32]

seen [34.25]. The photodissociation of ozone in the uv

range has been the target of many experimental stud-

ies [34.31]. The interpretation of the many experimental

results on the basis of realistic potential energy surfaces

is a great challenge for theoretical chemistry.

Photodissociation studies are particularly rewarding

if the lifetime in the excited electronic state is long be-

cause then the absorption spectrum shows well resolved

lines (resonances), the widths of which are inversely re-

lated to the state-speciﬁc lifetimes [34.33]. A typical

situation is the excitation of a particular vibrational-

rotational state in a bound electronic state which can

decay only via coupling to a dissociative electronic state.

The lifetime then reﬂects the coupling of this state to the

continuum of the dissociative state (predissociation). An

example is the photodissociation of HCO [34.34, 35];

in this case, the upper and the lower state are coupled

by Renner–Teller coupling. A similar example is the

photodissociation of HNO. For this molecule, the lower

state has a deep potential well which supports long-lived

states in its own continuum. The mixing between the

quasi-bound states of the upper state with the resonance

states of the lower state leads to interesting behavior

in the lifetime as a function of the rotational quantum

number [34.36] (resonance between resonances).

Resonances are also prominent features of ground

state potential energy surfaces; they are the continuation

of the true bound states into the continuum (Sect. 34.4.2).

Since resonances determine the kinetics of chemical

reactions, they are usually studied in the framework

of unimolecular dissociations or unimolecular reac-

tions [34.37]. On the other hand, these resonance states

can be excited by photons, and therefore it is meaningful

to discuss them also in the context of photodissoci-

ation. In the last few years, numerical methods have

been developed to efﬁciently calculate the resonance

parameters [34.38–40]; see [34.37] for a comprehensive

overview. Several triatomic molecules with dramatically

different intramolecular dynamics have been investi-

gated. The main observation is a strong ﬂuctuation in

the resonance lifetimes over several orders of magni-

tude, even for molecules whose classical dynamics is

chaotic, such as NO

[34.41]. Figure 34.5 shows the

results for HOCl → HO + Cl [34.32, 42]. The large

ﬂuctuations of the lifetimes (or dissociation rates) are

believed to affect the fall-off behavior of recombination

rate coefﬁcients [34.43].

The concept of ﬁrst calculating a potential energy

surface as function of all coordinates and then perform-

ing dynamics calculations is suitable only for triatomics.

For molecules with more than four atoms it is not

applicable, simply because of the rapidly increasing

number of degrees of freedom. For larger molecules,

direct dynamics simulations, in which the methodology

of classical trajectory simulations is coupled directly

to electronic structure calculations, are the method of

choice [34.44, 45]. In these simulations, the derivatives

of the potential, which are required for the numerical

integration of the equations of motion, are obtained

directly from electronic structure theory without the

need for an analytic potential energy surface. An im-

portant application of direct dynamics is the study

of post-transition state intramolecular and unimolecu-

lar dynamics. When the dissociation proceeds through

a transition state, it may be sufﬁcient to start trajectories

at the transition state and to follow them into the product

channels [34.46, 47]

34.6 Summary

Photodissociation of polyatomic molecules is an ideal

ﬁeld for studying the details of molecular dynamics.

The primary goal of the experimental and theoreti-

cal approaches (Sects. 34.2, 34.3) is to understand

the connection between the observables (Sect. 34.1)

and the underlying chemical dynamics (Sect. 34.4).

Part C 34.6