Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

Molecular Structure 31.2 Characterization of Potential Energy Surfaces 473

function for the ith helium atom in the natural orbital

basis [31.61] can be written as Ψ

=[1+ T

(i)]φ

(i),so

that the N atom electronic wave function becomes

Ψ =



[1+ T

(i)]Φ



exp



(i)



= exp(T

)Φ

(31.29)

Thus this exponential type of solution scales properly

with the number of particles.

To obtain the amplitudes t,deﬁneH

= H

−

Φ

|Φ

, E

0−CC

= ∆E

0−CC

+Φ

|Φ

≡

∆E

0−CC

+ E

0−0

, P =|Φ

Φ

| and Q = 1 − P. Then,

inserting (31.25–31.28)into(31.5)givestheenergy

(31.30) and amplitude (31.31) equations, which deﬁne

the coupled cluster approach:

∆E

0−CC

=Φ

|Φ

 , (31.30)

Φ

abc···

ijk···

|Φ

=0forallΦ

abc···

ijk···

, (31.31)

where

= exp(−T )H

exp(T)

=−E

0−0

+ exp(−T )H

exp(T ). (31.32)

To appreciate the nature of these equations, con-

sider the approximation T = T

constructed from SCF

orbitals [31.36, 59], referred to as the coupled cluster

doubles (CCD) level. At this level the energy equation

becomes

0−CCD

=Φ

| exp(−T

exp(T

)|Φ



=Φ

|Φ

+E

0−0

= E

0−0



i, j,r,s

†

= E

0−0



i, j,r,s

(rs||ij )t

(31.33)

for i, j occupied and r, s virtual orbitals. The amplitude

equations become

Φ

| exp(−T

exp(T

)|Φ



=Φ



1− T





1+ T



|Φ



= 0

(31.34)

which reduces (after considerable commutator alge-

bra) [31.36]to

(λ

+ λ

− λ

− (rs||ij ) −



p>q

(rs||pq)t

−



k>l

(kl||ij)t



k, p



(ks|| jp)t

− (kr|| jp)t

− (ks||ip)t

+ (kr||ip)t



−



k>l ; p>q

(kl|| pq)



− 2



+ t



− 2



+ t



+ 4



+ t



(31.35)

The solution to (31.35) is obtained iteratively. The

ﬁrst iteration gives t

=−(rs||ij )/(λ

+ λ

− λ

which when inserted into (31.33)gives(31.24), i. e.,

the MP2 result. If the quadratic terms in (31.35)are

neglected, then the second iteration gives the third or-

der Møller–Plesset (MP3) result [31.36]. The result of

iterating (31.35) to convergence gives the CCD result.

Of the levels of coupled cluster treatments in current

use, those including T

, T

,andT

in (31.25) provide

the most reliable results [31.62–66].

Multireference Methods

Single reference methods provide probably the most

powerful tools for treating near-equilibrium properties

of ground electronic state systems. In other instances,

such as the study of electronically excited states, de-

termination of global potential energy surfaces and for

systems with multiple open shells such as diradicals,

multireference techniques are found to be extremely use-

ful. In the multireference techniques discussed below,

the wave function is written as

0−MRF

(r; R) =



(r; R) (31.36)

where ψ

(r; R) is a CSF. This expansion is usually

referred to as a conﬁguration interaction (CI) expan-

sion, and the coefﬁcients c

(R) are referred to as CI

coefﬁcients [31.42]. Since (31.36) does not involve the

exponential ansatz, it is not automatically size extensive.

In the description of these wave functions, it is useful to

generalize the notion of occupied and virtual orbitals to

inactive, active, and virtual orbitals, where, referring to

the CSF’s deﬁning the reference space, inactive orbitals

are fully occupied in all CSFs, virtual orbitals are not oc-

Part C 31.2

474 Part C Molecules

cupied in any CSF and the active orbitals are (partially)

occupied in at least one CSF.

Most multireference techniques begin with the deter-

mination of a multiconﬁgurational self-consistent ﬁeld

(MCSCF) wave function or state averaged MCSCF

(SA-MCSCF) wave function [31.50–53, 67]. This ap-

proach is capable of describing the internal or static

correlation energy, the part of the correlation energy that

leads to sizeable separation of two electrons in a pair,

and near-degeneracy effects. A particularly robust type

of MCSCF wave function, the complete active space

(CAS) [31.68–70] wave function, includes in (31.36)all

CSFs arising from the distribution of the available elec-

trons among the active orbitals. Note that a CAS wave

function is size consistent.

The remaining part of the correlation energy, the dy-

namic correlation, describes the two-electron cusp, i. e.,

the regions of space for which two electrons experience

the singularity in the Coulomb potential. Empirically,

it has been shown [31.71] that wave functions cap-

able of providing chemically accurate descriptions of

the dynamic correlation can be obtained by augmenting

the MCSCF or reference wave function with all CSFs

that differ by at most two molecular orbitals, double

excitations (31.28) from those of the reference space.

Such wave functions are generally referred to as mul-

tireference single and double excitation conﬁguration

interaction (MR-SDCI) wave functions. First (second)

order wave functions [31.72] include all single (sin-

gle and double) excitations relative to a CAS reference

space.

Multiconﬁgurational Self-Consistent Field (MCSCF)

Theory.

In the MCSCF approximation, a wave func-

tion Ψ

0−MCSCF

(r; R) =



(r; R) of the form in

(31.36) is to be determined. In this procedure, both

the molecular orbitals φ(r

; R) andc

(R) are determined

from the requirement that

0−MCSCF



0−MCSCF

(r; R)



0−MCSCF

(r; R)



(31.37)

be a minimum. In a popular variant, the state aver-

aged MCSCF (SA-MCSCF) [31.50–53] procedure, the

average energy functional

0−SA−MCSCF



I=2



0−MCSCF

(r; R)



× Ψ

0−MCSCF

(r; R)



, (31.38)

where the weight vector w = (w

,... ,w

) has

only positive elements, is minimized. This procedure

should be compared with the multireference CI ap-

proach described below in which a predetermined set

of molecular orbitals is used.

The optimum molecular orbitals and CI coefﬁents

can be written as unitary transformations of an initial set

of such quantities, i. e.,

0−MCSCF

= exp(γ) exp(∆)Φ

, (31.39)

where

γ =



i,s

s,i

†

,∆=



n,l

∆

l,n







(31.40)

and γ ,∆ are general anti-Hermitian matrices. Since

i, j

=−m

j,i

≡ m

for m = γ ,∆, the upper triangle

of m forms a vector



m that enumerates the independent

parameters of m.TheMCSCF or SA-MCSCF equations

can be succinctly formulated by inserting (31.39)into

(31.37)or(31.38), expanding the commutators to second

order and requiring ∂E/∂m

= 0 [31.36]. The result pro-

vides a system of Newton-Raphson equations that can

be solved iteratively for the γ , ∆ [31.52, 53,67,73].

Multireference Conﬁguration Interaction Theory: The

MR-SDCI Method.

In multireference conﬁguration inter-

action theory, the wave function is again of the form

0−MRCI

(r; R) =



(R)ψ

(r; R), but now CSFs

involving the large space of virtual orbitals are included.

In this approach the CI coefﬁcients are found for a prede-

termined set of molecular orbitals. The CSF expansions

at the MR-SDCI level become quite large (1–10 mil-

lion CSFs is routine), and even larger expansions are

tractable using specialized methods. The c

satisfy the

usual matrix equation



− E



= 0 , (31.41)

where

αβ

=ψ

|ψ





i, j

αβ



i, j,k,l

αβ

ijkl

(ij|kl). (31.42)

It is the computationally elegant solution of (31.41)for

largeexpansionsthat is the essence of modern MR-SDCI

methods.

Because of the large dimension of the CSF space, it is

not possible (or even desirable) to ﬁnd all the solutions

of (31.41). The few lowest eigenstates and eigenval-

ues can be found [31.74] using an iterative direct CI

Part C 31.2

Molecular Structure 31.2 Characterization of Potential Energy Surfaces 475

procedure [31.75] in which a subspace is generated se-

quentially from the residual deﬁned at the kth iteration

(k)





µν

− E

(k−1)

µν



(k−1)

, (31.43)

where for simplicity of notation, the state index

I is suppressed. The computationally demanding

step in this procedure is the efﬁcient evaluation of

the A

αβ

ijkl

=ψ

− δ

|ψ

. Key to the efﬁ-

ciency of this evaluation is the factorization formally

achieved by

ψ

|ψ

=



ψ

|ψ

ψ

|ψ

 .

(31.44)

Using unitary group techniques, this apparently in-

tractable summation can be used to express the A

µν

ijkl

as a simple ﬁnite product [31.76].

Contracted CI and Complete Active Space Perturba-

tion Theory (CASPT 2).

The direct approach outlined

above makes treatment of large MR-SDCI expansions

possible. However, as the size of the reference space

grows, the CSF space in the MR-SDCI expansion may

become intractably large, particularly if the full second-

order wave function is used. To avoid this bottleneck,

the reference CSFs may be selected from the active

space, and perturbation theory may be used to select

CSFs involving orbitals in the virtual space [31.42].

The use of selection procedures complicates the im-

plementation of ‘direct’ techniques although recently

progress in selected direct CI procedures has been re-

ported [31.77–79]. Alternatively, new techniques have

been developed that avoid this selection procedure. In

these approaches, the MCSCF wave function itself is

used as the reference wave function for CI or pertubation

theory techniques. The use of a reference wave function

rather than a reference space considerably reduces the

size of the CSF space to be handled. In this approach,

one of the principal computational complications is

that the excited functions are not necessarily mutually

orthogonal. Two computational procedures currently

in wide use, known as contracted CI [31.80–83]and

CASPT2 [31.84,85], are based on this approach.

The CASPT2 method is a computationally efﬁcient

variant of second order perturbation theory in which the

reference wave function is a CAS-MCSCF wave func-

tion and thus may itself contain tens of thousands of

CSFs. In this case the full multireference CI problem

would be intractable owing to the large space of double

excitations. A similar approach is adopted in the con-

tracted CI method, in that the excitations are deﬁned

in terms of a general MCSCF reference wave func-

tion Ψ

0−MRF

rather than the reference space as in the

MR-SDCI methods described above.

31.2.3 Electron Correlation:

Density Functional Theory

The approaches in Sect. 31.1.1 and 31.1.2 can be re-

ferred to as wave function based approaches in the

sense that determination of E

(R) is accompanied by

the determination of the corresponding electronic wave

function Ψ

(r; R). An alternative approach is known as

density functional theory (DFT) [31.86]. The ultimate

goal of DFT is the determination of total densities and

energies without the determination of wave functions,

as in the Thomas–Fermi approximation. DFT is based

on the Hohenberg–Kohn Theorem [31.87], which states

that the total electronic density can be considered to be

the independent variable in a multi-electron theory (see

also Chapt. 20). Computationally viable approaches ex-

ploit the Kohn and Sham formulation [31.88], which

introduces molecular orbitals as an intermediate device.

The essential features of the Kohn–Sham (KS)the-

ory [31.86] are as follows [31.89]. Assume that the

real N-electron system for a particular arrangement

of the nuclei R has a total electron density ρ(r; R).

Consider a system of N independent noninteracting

electrons subject to a one-body potential V

with to-

tal density ρ

(r; R) such that ρ(r; R) = ρ

(r; R).The

corresponding independent particle orbitals, the Kohn–

Sham orbitals φ

; R), satisfy a Hartree–Fock-like

equation



−

∇

+ V

− ε



= 0 (31.45)

with

(r; R) =



|φ

. (31.46)

The relation between the energy of the ideal system and

that of the true system E

0−DFT

(R) is obtained from the

adiabatic connection formula [31.89].

In order to determine E

0−DFT

(R), functions φ

are

required, which in turn means that V

, the Kohn–Sham

noninteracting one-body potential, must be determined.

is written as (31.3)

= V

e−N

+ V

Coul

+ V

(31.47)

where V

Coul

is the Coulomb interaction corresponding

to the electron density, V

e−N

is the electron-nuclear at-

Part C 31.2

476 Part C Molecules

traction interaction and V

is the exchange-correlation

density. The effect of (31.47) is to isolate from V

the straightforward contributions V

Coul

and V

e−N

,and

transfers our ignorance to the remaining portion V

Although, by the Hohenberg–Kohn theorem V

must

exist, its determination remains the challenge of modern

density functional theory, which currently uses approx-

imate functional forms. These approximate treatments

of V

are quite useful in practice, and for large systems,

DFT offers a promising alternative to wave function

based methods.

Through (31.45), the KS approach is formally sim-

ilar to SCF theory, although the Kohn–Sham theory is

in principle exact. This formal similarity is exploited in

the evaluation of the derivative E

0−DFT

(R) [31.90].

31.2.4 Weakly Interacting Systems

When attempting to describe weak chemical interac-

tions such as van der Waals or dispersion forces, the

techniques outlined in Sect. 31.2.2 must be modiﬁed

somewhat. These modiﬁcations arise from the ﬁnite-

ness, and hence incompleteness, of the basis (the set χ)

used to describe the molecular orbitals. Assume that

the interaction of two molecules A and B is to be de-

termined. Consider the description of molecule A as

the distance between A and B decreases from inﬁn-

ity. The atom centered basis functions on molecule B

augment those on molecule A, lowering its energy, inde-

pendent of any physical interaction. This computational

artifact serves to overestimatethe interaction energy, and

is known as the basis set superposition error [31.91,92].

In chemically bonded systems where interaction ener-

gies are large, it is of negligible importance. However in

weakly bonded systems for which the interaction ener-

gies may be on the order of 10 to 100 cm

−1

, the basis

set superpostion error can be signiﬁcant.

The basis set superposition error can be reduced by

the counterpoise correction [31.93,94]. In this approach,

the interaction energy is evaluated directly as

0−int

(R) = E

(R) −



0−A

(R) + E

0−B

(R)



(31.48)

where E

0−A

(R) and E

0−B

(R), the energies of A and B

respectively, are evaluated in the full basis.

31.3 Intersurface Interactions: Perturbations

The existence of interstate interactions can lead to ‘unex-

pected’ shifts in spectral lines as well as predissociation

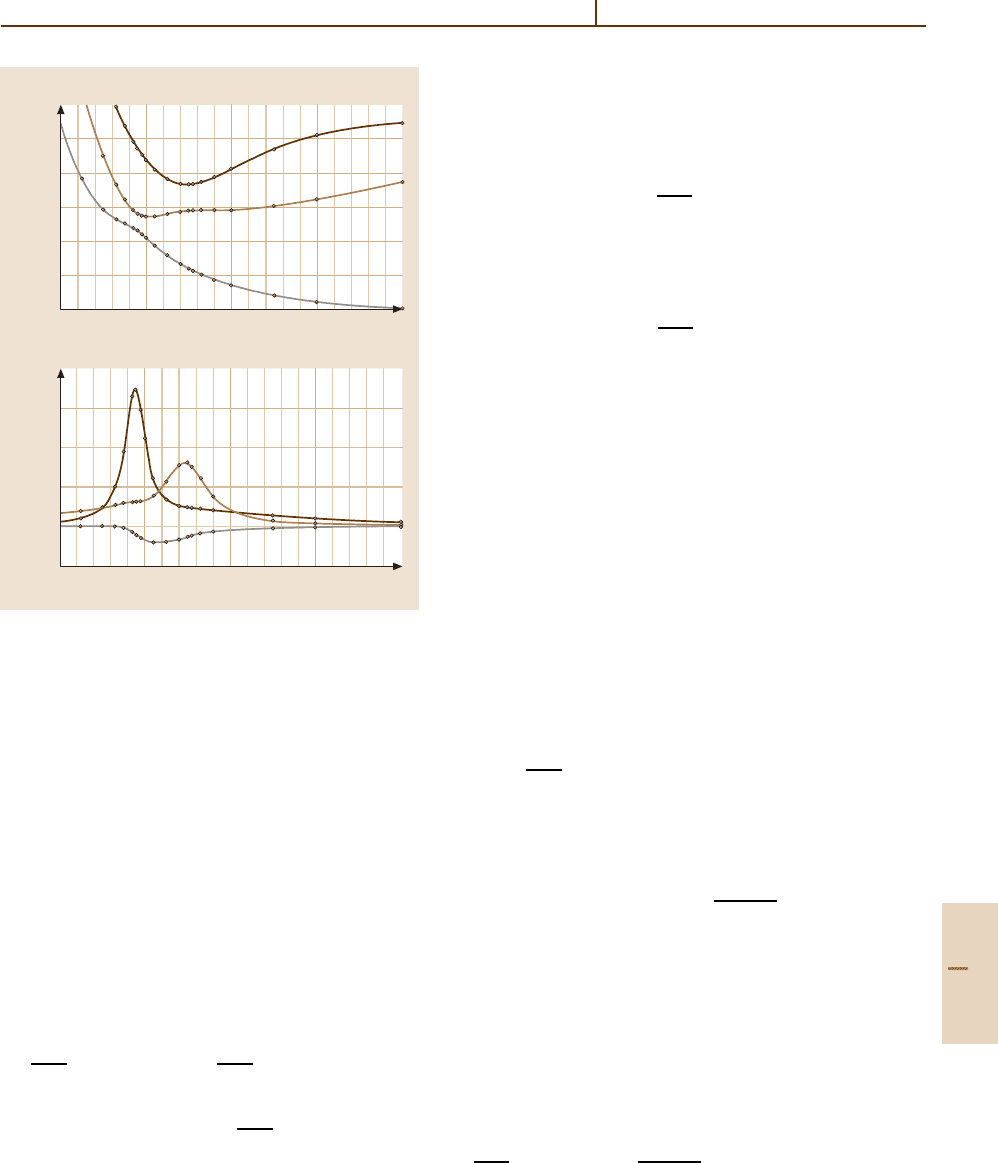
of the states themselves [31.95]. These situations are il-

lustrated in Fig. 31.2a,b which present the 1, 2, 3

potential energy curves for Al

and the corresponding

derivative couplings f

(R) respectively. The derivative

couplings were evaluated using the method described

in Sect. 31.3.1. In this molecule, derivative couplings

between the 2, 3

states are responsible for the

perturbations in the vibrational levels of the bound

2, 3

states. Derivative couplings of these states with

the 1

state causes predissociation of all levels in

the 2, 3

manifold [31.96].

Section 31.1 describes two classes of interstate

matrix elements that can lead to these nonadiabatic

phenomena, the derivative coupling matrix elements in

(31.7–31.10)andH

rel

, which is usually treated for low

Z systems within the Breit–Pauli approximation. An il-

lustration of a nonadiabatic process induced by H

rel

provided in Sect. 31.5. A key issue in the treatment of

the electronic structure aspects of these phenomena is

the reliable evaluation of the interstate matrix elements.

The interstate interactions are usually of most interest

in regions of nuclear coordinate space far removed from

the equlibrium nuclear conﬁguration. Thus it is desir-

able to evaluate these interactions using multireference

CI wave functions which (Sect. 31.1) are well suited for

use in these regions of coordinate space. The evaluation

of nonadiabatic interactions, based on SA-MCSCF/CI

wave functions, is discussed below.

31.3.1 Derivative Couplings

From (31.9–31.11), two classes of matrix elements are

required,

(R) and f

(R). In fact, techniques

to evaluate both of these exist [31.44]. However, it

is common to approximate

(R) by



(R) =





∂

∂W

(r; R)



(r; R)





(r; R)



∂

∂W



(r; R)







. (31.49)

with the (in principle inﬁnite) summation over states

truncated to reﬂect only the states explicitly treated in the

Part C 31.3

Molecular Structure 31.3 Intersurface Interactions: Perturbations 477

40 000

35 000

30 000

25 000

20 000

15 000

10 000

3.5 4.5 5.5 6.5 7.5

–1

3.5 4.5 5.5 6.5 7.5

E(cm

–1

)

R(Al – Al) (a

)

R(Al – Al) (a

)

–1

)

Fig. 31.2 (a) Adiabatic potential energy curves for the

1, 2, 3

states of Al

from [31.96]. (b) Derivative coup-

lings F

(R) for (I, J) = 1, 3

, 1, 2

and 2, 3

from [31.96]

nonadiabatic dynamics. Thus it is sufﬁcient to discuss

the determination of f

(R).

The use of analytic derivative theory [31.97, 98]

greatly improves the computational efﬁciency of eval-

uating f

(R) relative to the earlier divided difference

techniques [31.99]. The key ideas are given below. In this

presentation, the standard, real-valued normalization is

used. Additional contributions owing to the geometric

phase, if required, must be evaluated separately as they

do not follow from the electronic Schrödinger equation

at a single point [31.100].

Differentiation of the Ψ

(r; R) deﬁned in (31.36)

gives:

∂

∂W

(r; R) =





∂

∂W

(R)



(r; R)

+ c

(R)



∂

∂W

(r; R)



(31.50)

Thus f

(R), consists of two terms

(R) =

(R) +

CSF

(R), (31.51)

where the CI contribution is given by

(R) =



(R)



∂

∂W

(R)



, (31.52)

and the CSF contribution has the form

CSF

(R)



λ,µ

(R)



(r; R)



∂

∂W

(r; R)



(R).

(31.53)

Evaluationof

CSF

(R) is straightforward using analyt-

ical derivative techniques [31.101], so that the remainder

of the discussion focusses on

(R).From(31.52),

it would appear that the derivative of the CI coefﬁcients

∂/∂W

(R) ≡ V

,λ

(R) would be required to evaluate

(R). This is quite costly and is in fact not neces-

sary, since only the projection onto the state Ψ

(r; R)

is required. Equation (31.52)for

(R) can be recast

in a form similar to that of g

(R). This transformation

of (31.52) enables the explicit determination ofV

(R)

to be avoided, and is the key to the efﬁcient use of

analytic gradient techniques in the evaluation of f

(R).

Differentiating (31.41) with respect to W

gives



− E

(R)



(R)

=−



∂

∂W



− E

(R)





(R). (31.54)

Taking the inner product of (31.54) with c

(R) gives

(R) ≡ c

(R)

†

(R) (31.55)

= ∆E

(R)

−1

(R)

†

∂ H

(R)

∂W

(R)

(31.56)

≡ ∆E

(R)

−1

(R). (31.57)

Observe that (31.56)and(31.57) are not the Hellmann–

Feynman theorem [31.101, 102](Chapt.51), to which

they bear a formal resemblance, since it is not the

Hamiltonian operator H

(r; R) but rather the Hamil-

tonian matrix H

(R) that is being differentiated. Since

the energy gradient has the form [31.44]

∂

∂W

(R) = c

(R)

†

∂ H

(R)

∂W

(R), (31.58)

Part C 31.3

478 Part C Molecules

its relation to

(R) is clear. This identiﬁcation is the

keystepintheevaluationof

(R) using analytic

gradient techniques [31.97,98].

31.3.2 Breit–Pauli Interactions

For light systems, it is possible to introduce relativistic

effects using the Breit–Pauli approximation [31.1], in

which the four component Dirac description of a sin-

gle electron is replaced by a two component (α, β)

description. The H

(r; R) becomes [31.1,103]

(r; R) = H

(r; R) + H

rel

(r; R), (31.59)

where, in parallel with (31.4–31.13) for the atomic case,

the relativistic correction H

rel



k=1

(r; R) can be

divided into spin-dependent (SD) and spin-independent

(SI) parts, plus an external ﬁeld interaction term H

ext

These are given by

= H

≡ H

+ H

soo

+ H

, (31.60)

= H

≡ H

mass

+ H

ssc

+ H

(31.61)

= H

ext

, (31.62)

where, in atomic units,



K,i

− R

) × p

· s

− R

, (31.63)

soo

=−



i= j

× p

· (s

+ 2s

)



, (31.64)

= α



i< j



· s

−

3(r

· s

)(r

· s

)



(31.65)

mass

=−



, (31.66)

=−







K,i

∇

− R

−1

−



i= j

∇



−1





(31.67)

ssc

=−

8πα



i< j

· s

)δ(r

), (31.68)

=−







j=i

· p

−



· p







(31.69)

ext



E(r

) × p

· s

iα



E(r

) · p

+ 2µ



H (r

) · s

, (31.70)

E(r) and H (r) are electric and magnetic ﬁelds,

and µ = e

/(2m

) is the Bohr magneton. The phys-

ical signiﬁcance of these terms is discussed is

Sect. 21.1. One of the most important consequences

of these relativistic effects is that total electron

spin is no longer a good quantum number as it

is in H

(r; R).ThetermH

couple states corre-

sponding to distinct eigenvalues of S

and lead to

the nonadiabatic effects that are the subject of this

section.

The Breit–Pauli approximation is most useful for

light atoms, but the approximation breaks down when

Z becomes large [31.104–106]. One of the principal

effects omitted in a treatment which includes only

is the relativistic contraction of the molecular

orbitals [31.107] due to the mass-velocity operator

mass

), an effect whose importance increases with Z.

Several approaches exist which attempt to correct this

situation while retaining the spirit and simpliﬁcations

of the Breit–Pauli approximation. The ﬁrst of these is

the relativistic effective core potential (ECP) approxi-

mation [31.108–111]. In this approach, the results of

an atomic Dirac–Fock calculation [31.112]areusedto

replace innermost or core electrons of a given atom

with (i) an effective one electron potential that mod-

iﬁes the electron-nuclear attraction term in H

and

(ii) an effective one electron spin-orbit operator, so

that

(r; R) → H

e−ECP

(r; R)

= H

0−ECP

(r; R) + H

so−ECP

(r; R).

(31.71)

The formal similarity between H

e−ECP

and H

(r; R)

results in a similar phenomenological interpretation of

relativisticallyinduced nonadiabatic processes. Applica-

tions of this approach have been reviewed [31.107,113].

A second approach includes all electrons explic-

itly, and uses H

as deﬁned above. The relativistic

contraction of the core electrons is included by

using a variational one-component spin-free approxima-

tion [31.114, 115] to the no-pair Hamiltonian [31.116]

at the orbital optimization stage. The variational na-

ture of the approximation provides advantages over

the use of the H

mass

term. Applications of this ap-

proach to the spectra of CuH and NiH have been

reported [31.117,118].

Part C 31.3

Molecular Structure 31.3 Intersurface Interactions: Perturbations 479

In order to evaluate H

(R), it is necessary to

specify the molecular orbitals to be used to con-

struct the Ψ

(r; R). The choice of molecular orbitals

is dictated by the following considerations. Matrix el-

ements of H

between different states are required.

The molecular orbitals appropriate for one state may

not be appropriate for the description of the sec-

ond state. Two approaches are available to handle

this situation. In one approach, distinct sets of (mu-

tually nonorthogonal) molecular orbitals are used to

describe each state [31.119]. This permits a more com-

pact description of the spaces in question. However

in this case one is required to evaluate the ma-

trix element of a two electron operator H

soo

and/or

in a nonorthogonal molecular orbital basis, an

imposing computational task. This signiﬁcantly lim-

its the size of the CSF space which is tractable.

The alternative approach is to use a common or-

thonormal basis balanced between the two spaces in

question, and to use larger CSF spaces [31.120–122].

The use of a common orthonormal basis decreases

signiﬁcantly the computational effort required to eval-

uate the matrix elements. A symbolic matrix element

method [31.123] has been applied to H

, as described

in the review [31.124].

31.3.3 Surfaces of Intersection

The preceding subsections have considered what must

be calculated in order to characterize an electron-

ically nonadiabatic process. As noted in Sect. 31.1,

it is also necessary to consider where in nuclear

coordinate space electronic nonadiabaticity is impor-

tant. Nonadiabatic processes are important in regions

of close approach of the potential energy surfaces

with regions of surface intersections being of pre-

eminent interest. Until recently, these surfaces of

intersection were determined by indirect methods,

i. e., the potential energy surfaces were characterized,

and then the surface of intersection was determined.

This made the determination of these surfaces of

intersection a computationally daunting task. How-

ever, computational advances have made it possible

to determine these surfaces of intersection directly,

i. e., without prior determination of the individual

potential energy surfaces. This point is discussed

next.

A point on the surface of conical intersec-

tion of two states of the same symmetry, subject

to a set of geometric equality constraints of the

form C

(R) = 0, i = 1,... ,m, is determined from the

Newton–Raphson equations [31.125]

−







(R, ξ, λ) g

(R) h

(R) k(R)

(R)

†

000

(R)

†

000

k(R)

†













δR

δξ

δλ













(R) + ξ

(R) +



i=1

(R)

∆E

(R)

C(R)







(31.72)

where δR= R



− R,δλ = λ



− λ,δξ = ξ



− ξ, g

(R) ≡

∂∆ E

(R)/∂R

, k

(R) ≡ ∂C

(R)/∂R

, h

(R) ≡ c

I †

(R)H

(R)/∂R

(R) ,ξ and λ are Lagrange multipli-

ers, and Q

(R, ξ, λ) is a matrix of second derivatives

[31.125]. For two states of different symmetry, the ana-

logue of (31.72) is used with the terms related to ξ

omitted [31.126]. The excellent performance of this

algorithm has been documented [31.125,127].

Equations (31.72) can be motivated as follows. R

sought so that E

(R) is minimized subject to the con-

straints E

(R) = E

(R) andC(R) = 0. The key is to

impose the ﬁrst of these constraints, noting that at each

step in the Newton–Raphson procedure,c

(R) andc

(R)

are eigenvectors. Equation (31.72) are the Newton-

Raphson equations corresponding to the Lagrangian

function [31.128]

(R, ξ, λ) = E

(R) + ξ

∆E

(R)

+ ξ

(R) +



k=1

(R),

(31.73)

provided that the gradient of H

(R) is interpreted as

a change in H

(R) within the subspace spanned by

(R) and c

(R). This can be derived from quaside-

generate perturbation theory and understood as follows.

Assume for convenience that m = 0, i. e., there are no

geometrical constraints.

Consider an R for which (31.72) is not satisﬁed.

The 2 × 2 matrix H(R) with matrix elements H

(R),

K, L ∈{I, J} becomes at R+ δR

(R+ δR)

= c

I †

(R)

H(R) +



∂ H(R)

∂R

δR

(R),

(31.74)

Part C 31.3

480 Part C Molecules

H(R) is diagonal but nondegenerate at R,i.e.,

H(R) =

(R) − E

(R) 0

(31.75)

From (31.74)atR

= R+ δR, H(R

) becomes, to ﬁrst

order, ignoring an irrelevant uniform shift of the diagonal

elements,

H(R

) =

∆E

(R) + g

IJ †

· δRh

IJ †

· δR

IJ †

· δR 0

(31.76)

Thus (31.72) is seen to be the requirement that H(R

)

has degenerate eigenvalues, with eigenvectors c

(R) and

(R).When(31.72) have been solved, H

) is di-

agonal and degenerate, E

) has been minimized, and

) = 0, except along directions contained in the two

dimensional subspace spanned by g

) and h

From (31.76), it is these two directions which lift the

degeneracy ofH(R

). Equation (31.72) is also relevant

to the reaction path in a nonadiabatic process as dis-

cussed in Sect. 31.4. A discussion of these points from

an alternative perspective has been presented by Radazos

et al. [31.129].

A solution to (31.72) is referred to as a conic-

al intersection, although rigorously degenerate states

cannot be obtained from a numerical procedure.

If required, the existence of a conical intersec-

tion can be rigorously established by showing that

the adiabatic wave functions undergo a change of

sign when transported around a closed loop con-

taining R

in the plane deﬁned by g

) and

). This is the geometric or Berry phase crite-

rion [31.130, 131]. It has been explicitly demonstrated

for a conical intersection in O

by Ruedenberg and

coworkers [31.132].

31.4 Nuclear Motion

31.4.1 General Considerations

The determination of the rovibrational spectrum of

polyatomic systems from ﬁrst principles is a problem

of primary importance since it allows the deter-

mination of molecular forces and structure from

spectral data. In the adiabiatic case, the solution

of (31.6)



nuc

(R) + E

(Q) − E



(R) = 0 (31.77)

is sought, where Q denotes a set of internal nuclear coor-

dinates. The reliability of the solution of (31.77) reﬂects

the accuracy of the Born–Oppenheimer potential energy

surface E

(Q) appearing in that equation. The meth-

ods for determining E

(Q) were discussed in Sect. 31.2.

Conversely, the determination of the E

from spectro-

scopic measurements can be used to infer information

concerning E

(Q). In either case, the accurate solution

of (31.77) is requisite and this section is concerned with

its solution.

The operator in (31.77) has a continuous spectrum

since T

nuc

includes translations of the nuclear center

of mass (cm). An operator with a discrete spectrum

is obtained by replacing the Hamiltonian in (31.77)

with one in which the translation of the nuclear c.m.

has been eliminated by transforming to the c.m. frame.

In the center of mass frame, (31.77) has the general

form [31.133]



(Ω, Q) + T

vib

(Q) + E

(Q) − E



β( , Q) = 0

(31.78)

where Ω are three rotational coordinates and T

and

vib

are the rotational and vibrational kinetic energy op-

erators. In T

(Ω, Q) all the complexity associated with

the coupling of nuclear and electronic angular momen-

tum is buried. The determination of the appropriate form

for (31.78) is by no means straightforward [31.134,135],

and treatment of the effects of multiple angular mo-

mentum is a complex problem in angular momentum

algebra.

In diatomic systems, the vibrational problem

involves only one internal coordinate and is straightfor-

ward. Angular momentum coupling is usually treated

using Hund’s case (a), (b), etc., or an intermediate

case approach [31.95] with Van Vleck’s reversed an-

gular momentum commutation relations being helpful

in analyzing the coupled angular momentum prob-

lem [31.134].

Polyatomic systems introduce new complications,

since in addition to the increased dimensionality of

the vibrational problem, internal and rotational coor-

dinates interconvert for colinear arrangements of the

nuclei; this is particularly relevant in triatomic systems.

In addition, since the C

∞v

point group has doubly degen-

erate representations at collinear geometries, electronic

Part C 31.4

Molecular Structure 31.4 Nuclear Motion 481

state degeneracies may arise (the Renner–Teller ef-

fect) [31.32,136,137], further complicating the analysis.

Techniques associated with the description of triatomic

systems involving coupled angular momentum and elec-

tronic degeneracy are illustrated in Sect. 31.4.3.

More generally, (31.78) can be rewritten as



(Ω, Q

) + T

vib

(Q) + E

sep

(Q) − E



β(R)

=−∆T

(Ω, Q)β(R) − ∆E

(Q), (31.79)

where

∆T

(Ω, Q) ≡ T

(Ω, Q) − T

(Ω, Q

), (31.80)

∆E

(Q) ≡ E

(Q) − E

sep

(Q), (31.81)

is an equilibrium structure, and E

sep

(Q) is a separa-

ble function of the normal coordinates. In this case, the

solution to the left-hand side of (31.79) can be factor-

ized into a rotational part and a vibrational part [31.138]

according to



(θ, χ)



) (31.82)

where D

is a symmetric top wave function [31.139],

and α

) is a pure vibrational wave function, e.g.,

harmonic oscillator function, for the ith internal normal

coordinate. It is in this approximation that the notion

of a molecule rotating and vibrating about a ﬁxed mo-

lecular structure is achieved. In this case, E

is just

the sum of the pure rotational and vibrational energies.

These rigid rotator-vibrator solutions then form the basis

for the inclusion of the effects of the right-hand side us-

ing, for example, perturbation theory [31.140]. They can

also be used as a basis for a nonperturbative treatment

(Sect. 31.4.2).

The classic treatments of (31.77) [31.141–144]have

been periodically revisited [31.134, 145]. In these in-

vestigations, the contributions of electronic angular

momentum to this Hamiltonian were frequently sup-

pressed [31.144] so that these treatments are appropriate

to totally symmetric electronic states. Van Vleck [31.134]

has shown how the effects of electronic angular momen-

tum can be incorporated into these treatments.

For nonlinear polyatomic systems, the Hamiltonian

in (31.78) can be transformed to the Eckart or body

ﬁxed frame in which the reference axis is a body

ﬁxed axis oriented along the principal moments of in-

ertia [31.146], although other choices of the body ﬁxed

axes are possible [31.147]. The principal moments of

inertia represent the eigenvectors of the inertial tensor

matrix I

, i, j = x, y, z, where [31.144]



· R

− X

), (31.83)

=−



), (31.84)

and cyclic permutations, and R

denotes an equilibrium

structure. The Hamiltonian determined by this proce-

dure is referred to as the Watson Hamiltonian [31.145],

and is widely used in discussing the rovibrational

spectrum of nonlinear polyatomic molecules in singlet

electronic states. Treatments of the Watson Hamilto-

nian are mentioned in Sect. 31.4.2. For linear molecules,

an alternative treatment is required since there is one

feweroverall rotational coordinate and one more internal

coordinate [31.138].

31.4.2 Rotational-Vibrational Structure

Various approaches to the solution of (31.79) exist. The

principal issues, which are interrelated, are (i) the range

of nuclear conﬁgurations over which E

(Q) is known,

(ii) the coordinate system used to express the internal

coordinates, and (iii) particularly in larger systems, the

number of modes or internal coordinates retained in the

calculations (Sect. 31.4.3). With regard to point (i), two

approaches are currently in use. The force ﬁeld method

uses a power series expansion of E

(Q) about E

that is (using the Einstein summation convention)

(Q) = E

) +

∂

)

∂Q

∆Q

∂

)

∂Q

∆Q

(31.85)

together with perturbation theory to determine spec-

troscopic constants. In this approach, the force ﬁelds

[the partial derivatives in (31.85) are usually eval-

uated directly with the aid of analytic gradient

techniques (Sect. 31.2). Since the expansion of E

(Q)

is truncated, the results are not independent of the

coordinate system used. For example, signiﬁcant differ-

ences in the description of Fermi-resonance parameters

[31.148, 149] in rectilinear and curvilinear coordi-

nates [31.150] have been reported.

Alternatively, E

(Q) can be represented by a grid

of points around Q

. In the most reliable calcula-

tions reported to date, E

(Q) is determined using

the coupled cluster techniques discussed in Sect. 31.2.

Then (31.79) can be solved in a basis analogous to

Part C 31.4

482 Part C Molecules

in (31.82). This approach is frequently referred

to as the vibrational CI problem [31.151]. The relia-

bility of the results depends to a considerable extent

on the basis functions and coordinate system used to

describe the problem. Considerable success has been

reported for a technique in which the Watson Hamil-

tonian and harmonic oscillator functions are used to

solve (31.79) [31.151,152].

31.4.3 Coupling of Electronic

and Rotational Angular Momentum

in Weakly Interacting

An understanding of the molecular structure of the

weakly bound compounds of noble gas atoms and

diatomic molecules provides important insights into

the nature of chemical bonding. The inference of

structural data from spectroscopic observations is an

important aspect of this problem. In this subsec-

tion, a theoretical framework for understanding the

spectroscopy of these systems is outlined as an il-

lustration of the methods used to treat coupling of

electronic and nuclear angular momentum in weakly

interacting triatomic molecular systems. Detailed dis-

cussion of this class of problems can be found

in [31.153–155].

As an example, consider the rovibronic structure

of a noble gas-diatom complex Rg-AB, in either its

Π states (which may be closely spaced). Note

that degeneracy of the

Π state will only persist for

collinear geometries of the triatom system. The rovi-

brational wave functions can be expanded in a product

basis of functions describing (i) the rovibronic struc-

ture of AB and (ii) the relative motion (vibrational and

end-over-end rotation) of Rg and AB. Since total angu-

lar momentum J and its space ﬁxed projections M are

good quantum numbers, the rovibronic wave function

can be expanded as



v jΩlε

jΩlεv

(R)

×|ψ

|v

|IjΩε, l; JM , (31.86)

where ψ

is the ground state wave function for the

noble gas atom, l denotes the angular momentum asso-

ciated with the end-over-end motion, and v, j,εand I

denote respectively the vibrational, angular momentum

(electronic + rotational), e/f symmetry index and state

label of the electronic state of the AB molecule in

Hund’s case (a) basis. The angular momentum coup-

ling algebra noted above is reﬂected in the deﬁnition of

|IjΩε, l; JM,whichis

|IjΩε, l; JM



 jm

|JM Y

(θ, φ)ψ

Ijm

Ωε

(β, α) ,

(31.87)

where θ, φ and β, α are the polar and azimuthal an-

gles for the line connecting the noble gas atom to

the center of mass of the diatom and the diatom axis,

respectively, and ···|··· is a Clebsch–Gordan coef-

ﬁcient [31.156](Chapt.2). The ψ

Ijm

Ωε

are deﬁned in

turn by [31.95]

Ijm

Ωε



2J + 1

8π



1/2



,Ω

(α, β, 0)

∗

2S+1

(Σ )

+ εD

,−Ω

(α, β, 0)

∗

2S+1

−

(−Σ)



(31.88)

Ijm

Ωε



2J + 1

4π



1/2

× D

(α, β, 0)

∗

2S+1

Λ(Σ )

(31.89)

when Λ = Σ = 0, where the electronic state has term

symbol I

2S+1

Λ with Ω = Λ + Σ.

The C

(R) satisfy the usual close coupled equa-

tions [31.157,158] Sect. 47.1.1



−1

2µ

l(l+ 1)

2µR



I−

2µ

+ V(r)



(r)

= 0 ,

(31.90)

where l(l+ 1) and k

/2µ designate the diagonal matri-

ces of orbital angular momentum and asymptotic net

scattering energy of individual channels.V(R) repre-

sents the matrix elements of H

(r;R) in the vibronic

basis deﬁned in (31.86–31.89). It is built from terms of

the form



j ∗

Ω





2S+1



(r; R)



2S









∗



Ω





≡



j ∗

Ω





(R,

β,r)





∗



Ω





(31.91)

The angle

β is the polar angle of the diatom with respect

to the atom-diatom axis. The angular integrations on the

Part C 31.4