Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

Relativistic Atomic Structure References 357

22.74 J. Kaniauskas, Z. B. Rudzikas: J. Phys. B 13,3521

(1980)

22.75 G. Gaigalas, S. Fritzsche: Comput. Phys. Commun.

134, 86 (2001)

22.76 S. Fritzsche: Comput. Phys. Commun. 103,51

(1997)

22.77 S. Fritzsche, S. Varga, D. Geschke, B. Fricke: Com-

put. Phys. Commun. 111, 167 (1998)

22.78 G. Gaigalas, S. Fritzsche, B. Fricke: Comput. Phys.

Commun. 135, 219 (2001)

22.79 T. Inghoff, S. Fritzsche, B. Fricke: Comput. Phys.

Commun. 139, 297 (2001)

22.80 S. Fritzsche, T. Inghoff, T. Bastug, M. Tomaselli:

Comput. Phys. Commun. 139, 314 (2001)

22.81 L. V. Chernysheva, V. L. Yakhontov: Comput. Phys.

Commun. 119, 232 (1999)

22.82 C. F. Fischer, T. Brage, P. Jönsson: Computational

Atomic Structure. An MCHF Approach (Institute of

Physics Publishing, Bristol, Philadelphia 1997)

22.83 E. R. Davidson: J. Comput. Phys. 17, 87 (1975)

22.84 E. R. Davidson: Comput. Phys. Commun. 53,49

(1989)

22.85 A. Stathopoulos, C. F. Fischer: Comput. Phys. Com-

mun. 79, 268 (1994)

22.86 J. Olsen, M. R. Godefroid, P. Jönsson, P. Å. Malm-

qvist, C. F. Fischer: Phys. Rev. E 52, 4499 (1995)

22.87 P. Jönsson, C. F. Fischer: Phys. Rev. A 57, 4967 (1998)

22.88 Y Zou, C. F. Fischer: Phys. Rev. Lett. 88, 183001

(2002)

22.89 J. P. Desclaux, private communication, December

2003

22.90 J. Biero

n, P. Jönsson, C. F. Fischer: Phys. Rev. A 53,

1 (1995)

22.91 J. Biero

n, I. P. Grant, C. F. Fischer: Phys. Rev. A 58,

4401 (1998)

22.92 J. Biero

n, C. F. Fischer, I. P. Grant: Phys. Rev. A 59,

4295 (1999)

22.93 P. Jönsson, C. F. Fischer: Comput. Phys. Commun.

100, 81 (1997)

22.94 S. Fritzsche: J. Elec. Spec. Rel. Phenom. 114–116,

1155 (2001)

22.95 S. Fritzsche: Phys. Scr. T 100, 37 (2002)

22.96 S. Fritzsche, J. Anton: Comput. Phys. Commun. 124,

353 (2000)

22.97 S. Fritzsche, C. F. Fischer, C. Z. Dong: Comput. Phys.

Commun. 124, 340 (2000)

22.98 The CPC Program Library home page is at

http://www.cpc.cs.qub.ac.uk/cpc/

Part B 22

359

Many-Body Th

23. Many-Body Theory of Atomic Structure

and Processes

All atoms except hydrogen are many-body

systems, in which the interelectron interaction

plays an important or even decisive role. The aim

of this chapter is to describe a consistent method

for calculating the structure of atoms and the

characteristics of different atomic processes, by

applying perturbation theory to take into account

the interelectron interaction. This method involves

drawing a characteristic diagram based on the

structure or process. This is then used to create an

analytical expression to the lowest order in the

interelectron interaction. Higher-order corrections

are subsequently generated.

This technique was invented about half

a century ago in quantum electrodynamics by

Feynman [23.1], then modiﬁed and adjusted for

multiparticle systems by a number of authors.

Its application to atomic structure and atomic

processes required further modiﬁcations, which

were initiated at the end of the ﬁfties (see,

e.g., [23.2]) and later. The corresponding technique

was successfully applied to the calculation of

a wide variety of characteristics and processes

in many papers and several review articles

[23.3, 4]. The increasing amount of experimental

data available has led to improved accuracy

for this technique, so that it can be applied to

current problems considering not only atoms

and ions, both positive and negative [23.5–8],

but also molecules [23.9], clusters [23.10]and

fullerenes.

23.1 Diagrammatic Technique...................... 360

23.1.1 Basic Elements.......................... 360

23.1.2 Construction Principles

for Diagrams............................. 360

23.1.3 Correspondence Rules................ 362

23.1.4 Higher-Order Corrections

and Summation of Sequences..... 363

23.2 Calculation of Atomic Properties ........... 365

23.2.1 Electron Correlations

in Ground State Properties ......... 365

23.2.2 Characteristics

of One-Particle States ................ 366

23.2.3 Electron Scattering .................... 367

23.2.4 Two-Electron and Two-Vacancy

States ...................................... 369

23.2.5 Electron–Vacancy States............. 370

23.2.6 Photoionization

in RPAE and Beyond .................. 371

23.2.7 Photon Emission

and Bremsstrahlung .................. 374

23.3 Concluding Remarks ............................ 375

References .................................................. 376

The elements of the diagrammatic technique,

which form a convenient and simple “language”,

are given together with the rules for creating

“sentences” using basic “words”. A kind of

“dictionary” helps to translate diagrammatic

“sentences” into analytical expressions suitable

for calculations.

An essential part of the program is to learn how the sim-

plest approximation can be improved, and what are the

mechanisms and processes connected with, and respon-

sible for, higher-order corrections.

When the diagrammatic technique of many-body

theory is used, it is unnecessary to be restricted to a ﬁnite

number of lowest-order terms in the interelectron inter-

action. On the contrary, some inﬁnite sequences may

be taken into account. The sum of all many-body di-

agrams is completely equivalent to the many-particle

Schrödinger equation. Therefore, taking all of them into

account is just as complicated as solving the corre-

sponding equation. Compared with other approaches,

the diagrammatic technique can easily uncover hidden

approximations and transparently demonstrate possible

sources of corrections.

Part B 23

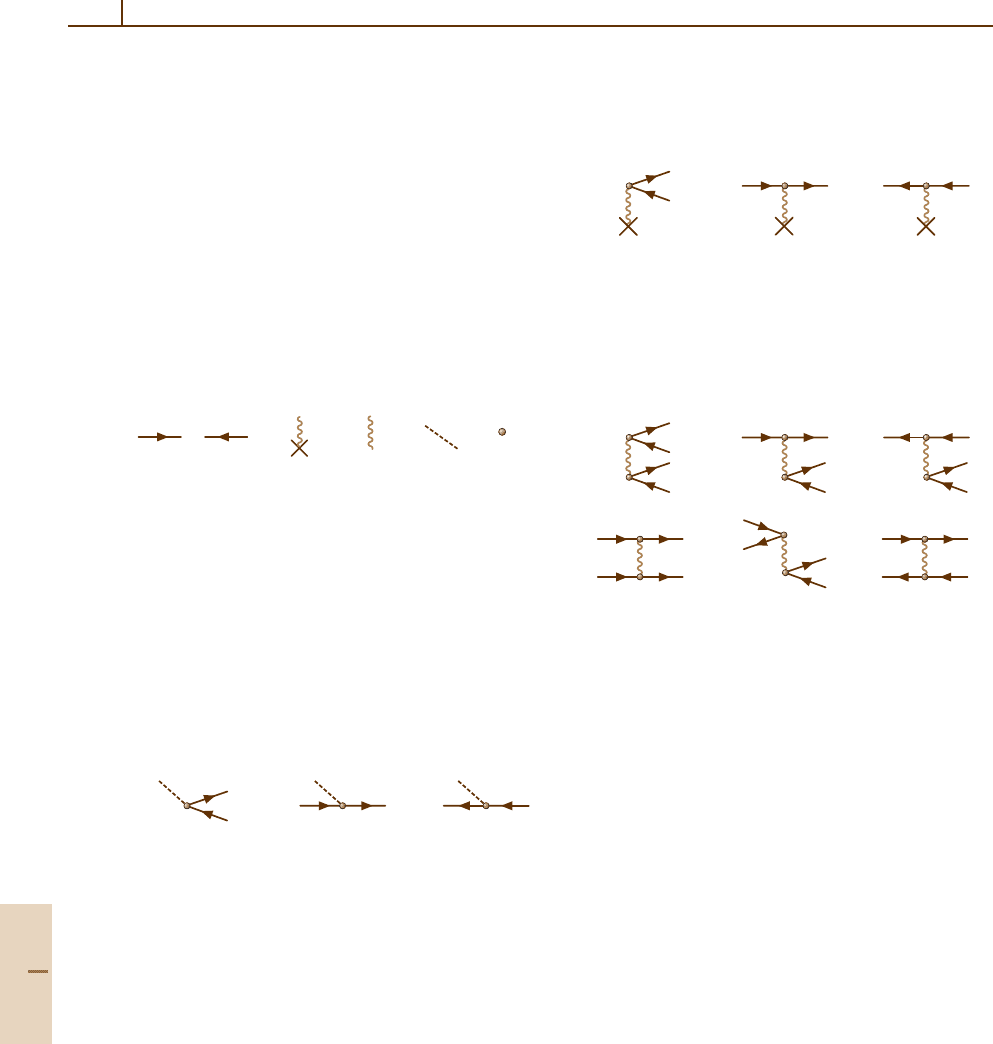
360 Part B Atoms

23.1 Diagrammatic Technique

23.1.1 Basic Elements

Each physical atomic process (or a process with par-

ticipation of a molecule, cluster or fullerenes) involves

an electronic interaction with a projectile or external

ﬁeld, in general time-dependent, or a mutual inter-

electronic interaction. By convention, the ground state

of the atom (if it is not degenerate) is regarded as the

vacuum state. Then the simplest process in this target is

excitation of an electron to an unoccupied level, leav-

ing behind a vacancy. The basic elements of a diagram

are

a) b) c) d) e) f)

(23.1)

where (a) with an arrow directed to the right represents

an electron excited to a vacant level; (b) with an arrow

directed to the left represents a vacancy; (c) with a cross

represents the static Coulomb interaction; (d) represents

the interelectron Coulomb interaction; (e) represents

interaction with a time-dependent external ﬁeld, usu-

ally electromagnetic; and (f ) represents the very act of

interaction.

The elements (23.1a–f) in combination can describe

the following real or virtual basic processes

a) b) c)

(23.2)

which represent (a) photon absorption by the vacuum

with electron–vacancy pair creation; (b) electron ex-

citation; and (c) vacancy excitation. Diagrams (23.2)

depict processes as developing in time, shown in-

creasing from left to right. A vacancy can be

thought of as an antiparticle to the electron, mov-

ing backward in time. The time-reverse of processes

(23.2) represent processes of photon emission due

to annihilation of an electron–vacancy pair, va-

cancy transition, and electron inelastic scattering,

respectively.

A static [for example, Coulomb (23.1c)] ﬁeld can

virtually create an electron–vacancy pair, or affect the

moving electron or vacancy, as shown in the following

diagrams:

a) b) c)

(23.3)

Just as for (23.2), diagrams (23.3) have their time-

reversed counterparts.

Inclusion of interelectron interaction leads to a num-

ber of processes of which some examples are

a) b) c)

d) e) f)

(23.4)

Here, (23.4a) describes creation of two electron–

vacancy pairs, (23.4b) represents the simplest picture

of electron inelastic scattering, (23.4c) depicts vacancy

decay with electron–vacancy pair creation, (23.4d)

stands for electron–electron scattering, (23.4e) repre-

sents a process which can be called electron–vacancy

annihilation and creation, while (23.4f ) shows electron–

vacancy scattering.

23.1.2 Construction Principles for Diagrams

The foundations of diagrammatic techniques are dis-

cussed in a number of books such as [23.11]. This

chapter presents recipes for the construction and eval-

uation of diagrams corresponding to various atomic

processes [23.12].

The basic procedure is to connect the initial and ﬁnal

states of the atom, drawn at the left and right sides of the

diagram, using any of the elements in (23.1). In doing

so, the following rules apply:

1. At each dot (23.1f), only three lines can meet: wavy

(or dashed) and electron–vacancy.

2. A vacancy cannot be transformed into an electron or

vice versa.

Part B 23.1

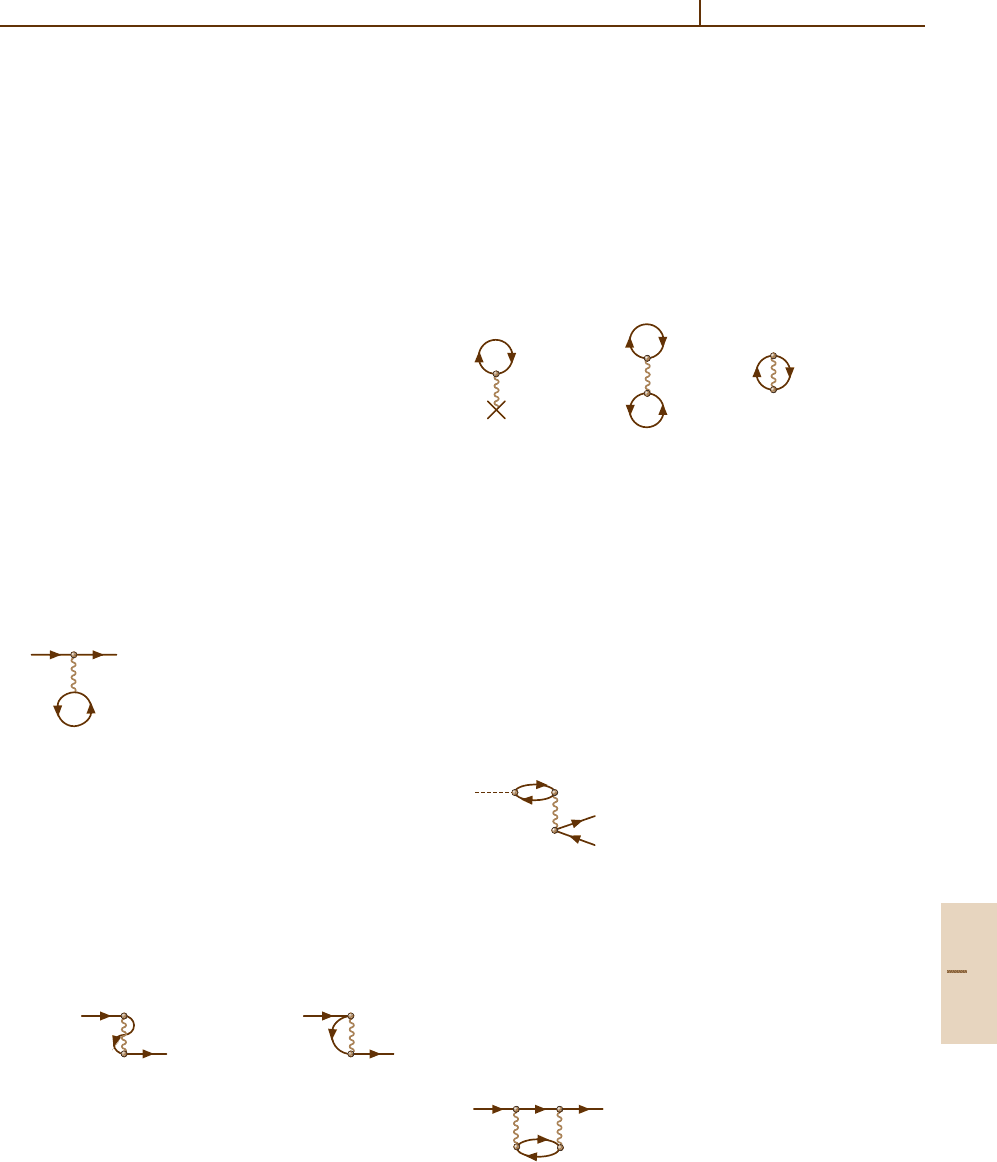
Many-Body Theory of Atomic Structure and Processes 23.1 Diagrammatic Technique 361

3. Electrons and vacancies can be created only pairwise

from the vacuum.

4. Only linked diagrams are allowed; i. e. only those

having no parts entirely disconnected from one an-

other.

The simplest or initial approximation to a process

is represented by a diagram which includes the lowest

possible number of elements (23.1–23.4). Higher-order

corrections can be derived by including additional

elements of interaction with the static ﬁeld of the

nucleus (23.1c) and between electrons and/or vacancies

(23.1d).

As an illustration of the method, consider the fol-

lowing three processes:

1. one-electron photoionization – the initial state is

a photon while the simplest ﬁnal state is an electron–

vacancy pair. They can be combined together giving

the basic diagram (23.2a).

2. elastic electron scattering – the initial and ﬁnal states

are single electrons. To describe the simplest scatter-

ing process, the interaction with the Coulomb ﬁeld

must be taken into account, leading to (23.3b). To

account for interelectron interaction, the simplest

element

(23.5)

must be introduced. It is a modiﬁcation of (23.4b)

accounting for the interaction of an incoming elec-

tron with all target electrons individually, not altering

their states. This is emphasized by the loop in which

the same vacancy leaving the lower dot reenters it.

Indistinguishability of all electrons as fermions is

taken into account by permutation of the electron

(vacancy) line ends, as illustrated in the following

diagrams:

a) or b)

(23.6)

Diagram (23.6a) is obtained from (23.5)byper-

mutation of the electron lines on one side of the

interelectron interaction. Diagram (23.6b) is equiva-

lent to (23.6a), but is simpler to draw.

3. inelastic electron scattering – the initial state is

a single electron. For the ﬁnal state we choose one

with two electrons and therefore a single vacancy.

The simplest diagram in this case is given by (23.4b).

To illustrate the description of the ground state char-

acteristics, consider the contributions to the ground state

energy of an atom. If this state is not degenerate, its po-

tential energy is given by vacuum diagrams which have

no free lines in the initial or ﬁnal states. The simplest

vacuum diagrams are

a) b) c)

(23.7)

Higher-order corrections to all these diagrams can be

obtained by adding elements such as a static external

ﬁeld (23.3) or interelectron interaction (23.4) without

changing the initial and ﬁnal states of the processes.

The lowest-order processes are represented by (23.2a),

(23.5), (23.6), (23.4b), and (23.7). There are many cor-

rections even in the next order of interaction, either with

an external ﬁeld or with electrons or vacancies. To il-

lustrate, only one correction to each process will be

presented:

1. Simple photoionization (23.2a) may be combined

with (23.4e) to obtain

(23.8)

This describes the effect of the creation of another

electron–vacancy pair, after annihilation of the ﬁrst

one formed by absorption of the initial photon.

2. Simple elastic electron scattering (23.5) can be

combined with an extra interaction term (23.4f) be-

tween the incoming electron and the vacancy of the

loop (23.5), to obtain

(23.9)

Part B 23.1

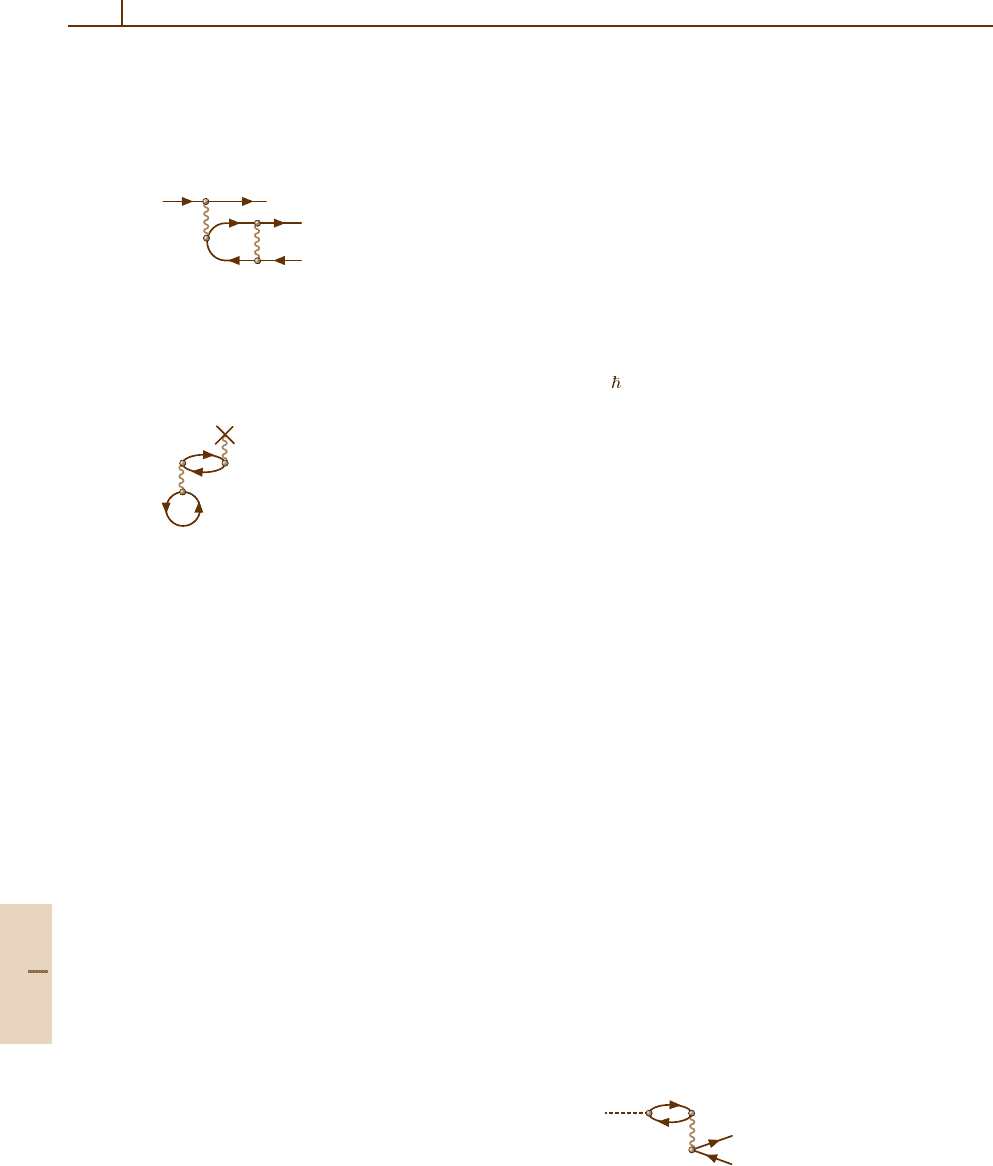
362 Part B Atoms

3. Simple inelastic electron scattering (23.4b) can also

be combined with (23.4f), accounting for the in-

teraction of an electron and vacancy created in the

lowest-order process, to obtain

(23.10)

4. The ground state energy term (23.7b) can be com-

bined with (23.7b) and the element (23.3c) of the

interaction between the vacancy in the (23.7b) loops

and the static ﬁeld to obtain

(23.11)

Higher-order corrections can be constructed step by

step by introducing further elements of interaction. In

some cases, classes of diagrams may be taken into ac-

count up to inﬁnite order by solving closed systems of

integral or differential equations.

23.1.3 Correspondence Rules

These rules describe how to obtain an analytical ex-

pression corresponding to a given diagram. One starts

by choosing a zero-order approximation which can be

that of independent electrons moving in the Coulomb

ﬁeld of an atomic nucleus. Atoms with completely occu-

pied shells, or subshells having a non-degenerate ground

state, can be chosen as the vacuum. Electron (vacancy)

states are characterized in this case by the quantum

numbers n, , m



,andσ =±1/2.

The ﬁrst correspondence rule is to substitute a matrix

element for each interaction:

Diagram (23.2) →p|W|q ,

Diagram (23.3) →p|U|q ,

Diagram (23.4) →pt|V|qs , (23.12)

where W is the interaction potential of an electron with

the external time-dependent ﬁeld, U is the interaction

potential of an electron (vacancy) with an external static

ﬁeld, for example that of the nucleus, and V is the

Coulomb interelectron interaction. Each of the letters

p, q, t, s represents a full set of n, , m



, σ quantum

numbers. Vacancy states are below (and include) the

highest occupied energy level, called the Fermi level,

so that p ≤ F. Electron states are above the Fermi level

so that q > F. Thus diagram (23.2a) is represented by

p|W|q with p ≤ F and q > F.

Apart from initial and ﬁnal states, each diagram can

have sections, i. e., intervals between successive inter-

actions. For instance (23.9)and(23.10) each have one

section. Each section is represented by an inverse energy

denominator ε

−1

. It includes the sum over all vacancy

energies



vac

minus the sum of the electron energies



to which the entrance energy E of the diagram

(e.g.

ω for a time-dependent ﬁeld) must be added:

−1





vac

−



+ E



−1

. (23.13)

The second correspondence rule is to identify sections

and write down their energy denominators. After at-

tributing to each electron (vacancy) line a letter, denoting

its state, the analytical expression for a diagram is given

Analytical Expression

= (the product of all interaction matrix elements)

× (all energy denominators)

−1

× (−1)

summed over all intermediate

electron and vacancy states,

(23.14)

where L is equal to the sum of the total number of

vacancy lines and closed vacancy or electron–vacancy

loops.

Although electrons are fermions, the summation

in (23.14) has no additional restrictions caused by the

Pauli principle. It runs over all electron (> F) and va-

cancy (≤ F) states, including those where two or more

electrons (or vacancies) are in the same state. The cor-

respondence rules (23.12), (23.13), and (23.14) can be

illustrated by giving as examples the analytical expres-

sions of two diagrams (23.8)and(23.9).

Attributing letters denoting electron and vacancy

states, diagram (23.8) becomes

(23.15)

Part B 23.1

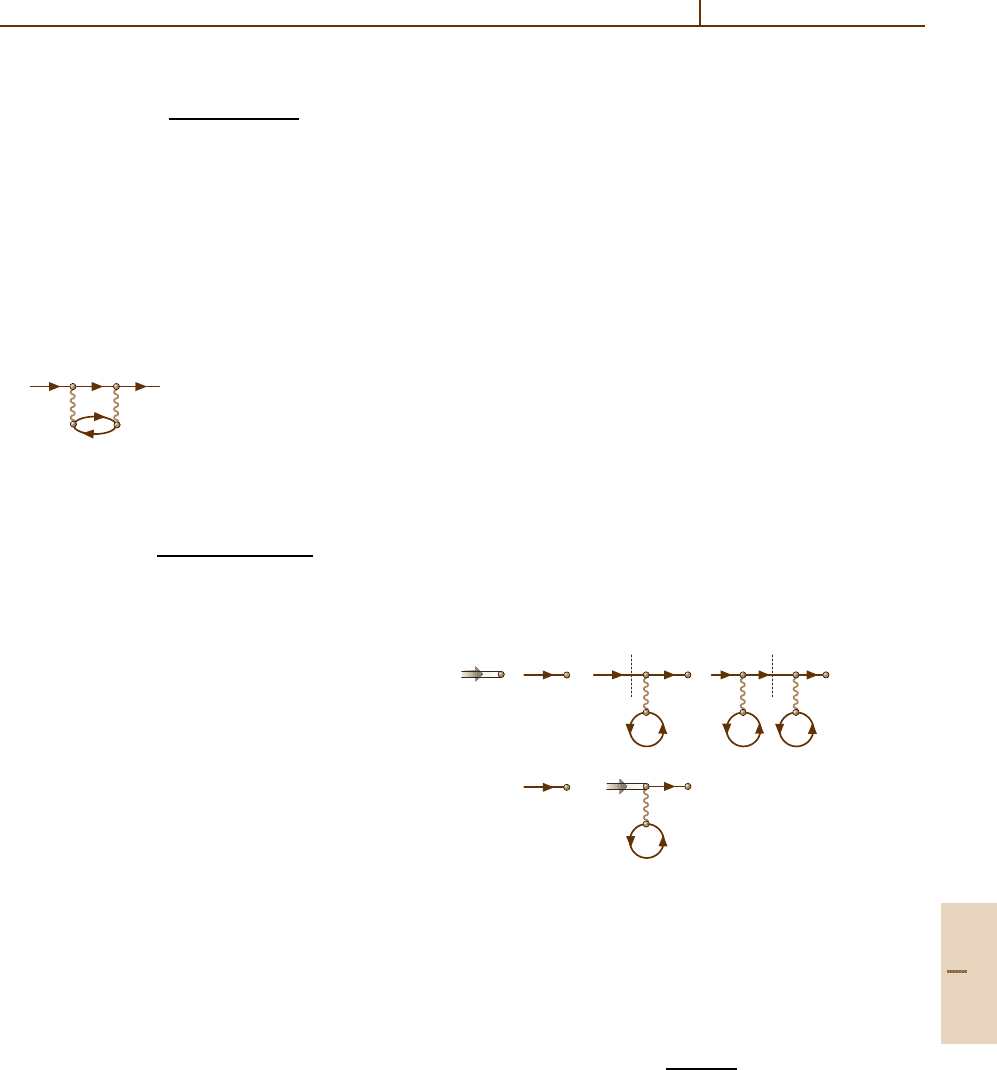
Many-Body Theory of Atomic Structure and Processes 23.1 Diagrammatic Technique 363

Accordingto(23.12–23.14), the analytical formula

(ω) =





r>F,t≤F

t|W|rri|V|tf

− ε

+ ω

(−1)

2+1

(23.16)

is obtained. The symbol





includes summation over

discrete levels and integration. In (23.16), the interme-

diate state is r > F, t ≤ F and the diagram has two

vacancies (t and i) and one loop rt. Integration must

be performed over those states r which belong to the

continuum.

Assigning letters denoting states, (23.9) appears as

pq p'

(23.17)

where p, q, p



, r > F, while t ≤ F. According to

(23.14),

∆E =





r,q>F;t≤F

pt|V|qrqr|V| p



t

− ε

+ ε

(−1)

1+1

(23.18)

where the intermediate states are q, r > F and t ≤ F.It

has one vacancy and one electron–vacancy loop rt.

An intermediate state in a diagram can be real or

virtual. It is real if the energy conservation law can be

fulﬁlled, i. e. if for some values of the section energy the

following relation holds:

E =



−



vac

. (23.19)

If (23.19) can be fulﬁlled, a prescription for avoiding

the singularity in (23.13) is to substitute the expression

−1

Q,where

Q = lim

η→0



E −



vac

+ iη



−1



E −



vac



−1

− iπδ



E −



vac



(23.20)

for ε

−1

.Here P denotes that the principal value is to

be taken on integration over intermediate state energies.

The result of (23.20) can thus be complex.

An intermediate state is virtual if the energy con-

servation law (23.19) is violated for all values of the

section energy. In general, the bigger the virtuality,

i. e. the difference E −



vac

, the smaller the

contribution to the amplitude of the process.

23.1.4 Higher-Order Corrections

and Summation of Sequences

An important feature of the diagrammatic technique is

the convenience in constructing higher-order corrections

and in the summation of inﬁnite sequences of diagrams.

According to (23.13), each new interaction line leads

to an additional interaction matrix element, extra en-

ergy denominator and summation over new intermediate

states.

An important example of inﬁnite summation

is that of determining the one-electron states.

The interaction with the nucleus (23.3b) and

with atomic electrons (23.5)and(23.6) is not

small and must be taken into account non-

perturbative; i. e., these elements must be iterated

inﬁnitely. To simplify the drawing, only the elem-

ent (23.5) is repeated, leading to the diagrammatic

equation:

= + + + ...

pppqpqq'

ii'

(23.21)

Indeed, everything in the inﬁnite sum which is in front

of the dashed line repeats the inﬁnite sum itself, thus

leading to a closed equation of the form



p|=p|+





q>F



pi|V|qi

−ε

+ ε

q| . (23.22)

The two interactions leading to (23.21) can be permuted,

so that the interaction 1 can be after 2. This leads to

Part B 23.1

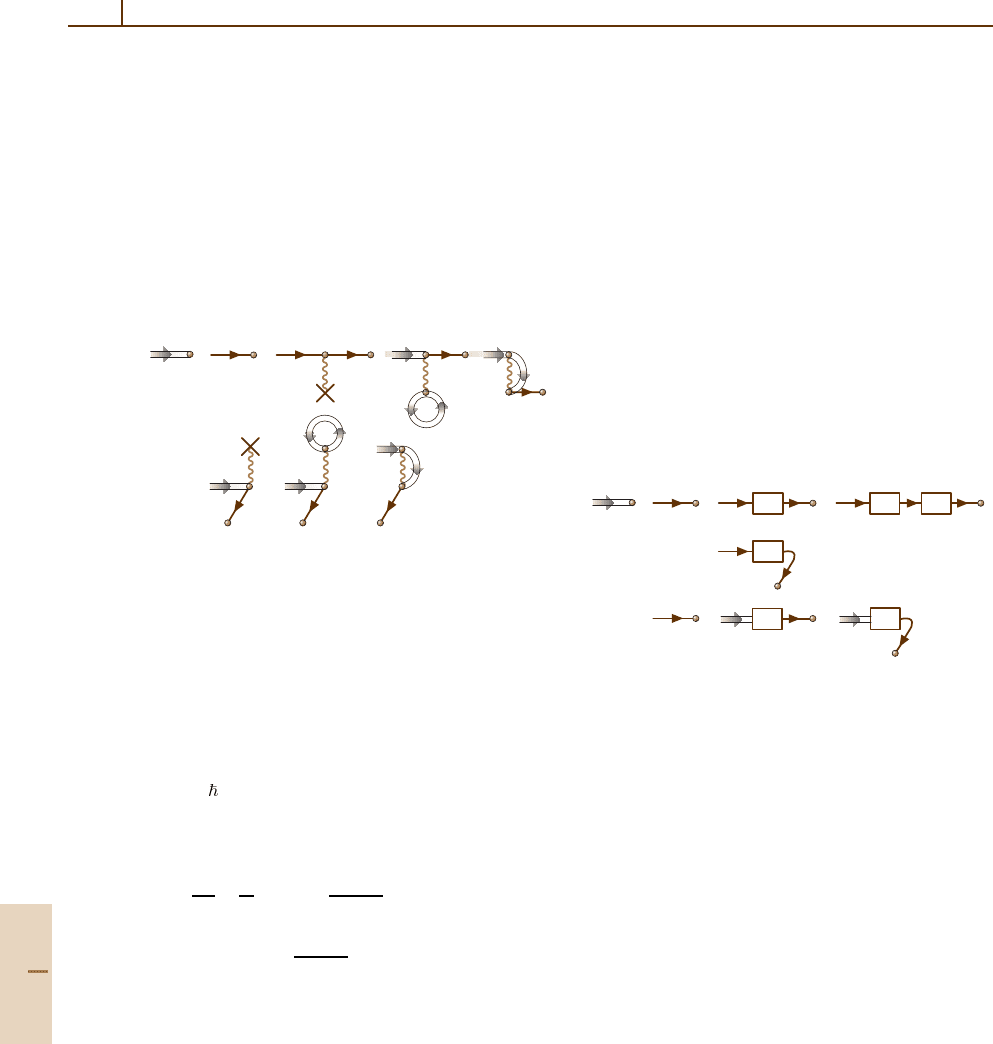
364 Part B Atoms

extension of the sum to include states with q ≤ F.As

a result, the summation in (23.22) must be performed

over all states q.

Interaction with the nucleus and the other elec-

trons affects also the occupied (or vacancy) states i

in (23.21) and therefore the latter must be modiﬁed by

inserting the elements (23.3b), (23.5), and (23.6)into

them. Here again, the vacancy line in (23.5)and(23.6)

must be modiﬁed by including the corrections (23.3b),

(23.5), (23.6) and so on. Finally, the diagrammatic

equation

=+ +

pppqpq

(23.23)

is obtained. The doubled line for i emphasizes that the

vacancy wave function is determined by an equation

similar to (23.21). The corresponding analytical equa-

tion looks like (23.22), but includes also the Coulomb

interaction with the nucleus and the exchange interac-

tion with other atomic electrons. The summation over q

in this equation is extended over all q, not only q > F.

Multiplying the corresponding equation by (

− ε

)

from the right (atomic units are used in this chapter:

e = m

= = 1),where

=−∇

/2, and using the

completeness of the functions





|qq|=δ(r − r



results in the equation



−

∇

−



i≤F



−r|

|φ



− ε



(r)



i≤F



−r|

∗



)φ



)φ

(r) (23.24)

for the electron wave function φ

(r).Hereφ

(r) are

wave functions determined by equations similar to

(23.24). These are the Hartree–Fock (HF) equations.

HF includes a part for interelectron interaction ma-

trix elements, namely that given by (23.5)and(23.6).

The rest is called the residual interaction, and its in-

clusion leads beyond the HF frame, accounting for

correlations.

When a perturbative approach is used, it is essential

to deﬁne the zero-order approximation. In this chapter,

and very often in the literature, the Hartree–Fock ap-

proximation is used in this role. To simplify the drawing

of diagrams, from now on single (rather than double)

lines will represent electrons (vacancies), whose wave

functions are determined in the HF approximation by

(23.24). Obviously, in this case elements (23.3a), (23.5)

and (23.6) should not be added to any other diagrams.

Theprocedureusedinderiving(23.21)and(23.23)

is in fact more general. Let us separate all diagrams de-

scribing elastic scattering which do not include a single

one-electron or one-vacancy state as intermediate. De-

picting their total contribution by a square, the precise

one-particle state is determined by an inﬁnite sequence

of iterative diagrams which can be summed, similarly to

(23.21), by

=+ +

pppq

pqq'

+…

…

(23.25)

Here the single line stands for an HF state. Using the

correspondence rule (23.14), an analytical equation sim-

ilar to the Schrödinger equation can be derived with the

operator

 playing the role of an external potential.

The essential difference is, however, that this “poten-

tial” depends in principle upon the energy and state of

the particle. The same kind of iterative procedure lead-

ingto(23.21)or(23.23) will be used several times in

this chapter.

Other zero-order approximations can be chosen.

But then diagrams with corrections of the type (23.3a)

must be included, with the external static ﬁeld potential

equal to the difference between the HF and the chosen

one.

To calculate the numerical value of a given dia-

gram or a sequence of diagrams one needs to know,

according to the description given above, the matrix

elements of external ﬁelds and interelectron interac-

tions obtained with the help of one-electron HF wave

functions. The required calculational procedures are

described in [23.13].

Part B 23.1

Many-Body Theory of Atomic Structure and Processes 23.2 Calculation of Atomic Properties 365

23.2 Calculation of Atomic Properties

23.2.1 Electron Correlations

in Ground State Properties

A major advantage of the diagrammatic technique in

many-body theory is that it is usually unnecessary to

know the total wave function of the atom. On the con-

trary, only actively participating electrons or vacancies

appear in a diagram. The HF zero-order approxima-

tion for one-electron and one-vacancy wave functions

is used in what follows. All atomic characteristics and

cross sections for atomic processes calculated with HF

form the one-electron approximation. Everything be-

yond the HF frame, i. e., caused by residual interaction,

are called correlation corrections or correlations. They

can be calculated using the many-body perturbation the-

ory (MBPT) [23.3], random phase approximation (RPA)

[23.14] and random phase approximation with exchange

(RPAE) or its generalized version GRPAE [23.12, 13].

The simplest diagrammatic expression for the corre-

lation energy is given by the two diagrams

a) b)

(23.26)

The analytical expression ∆E

(2)

corr

for (23.26a) is

∆E

(2)

corr





k,n>F;i, j≤F

ij|V|knkn |V|ij

+ ε

− ε

. (23.27)

The analytical expression for (23.26b) differs from

(23.27) by the sign and an exchange matrix element

kn|V| ji instead of a direct kn|V|ij one. The contri-

bution (23.26) overestimates the correlation energy by

≈10%.

Diagrams (23.26) can also be used to describe the

interaction potential of two atoms, designated A and B.

Let the ki states belong to A and njto B. At large dis-

tances R between the atoms, the contribution of (23.26b)

is exponentially small. Because the vacancies i and j

are located inside atoms A and B respectively, the

interelectron potential V =|r

−r

+ R|

−1

at large dis-

tances R  R

A,B

,(R

A,B

are atomic radii), can be

expanded as a series in powers of R

−1

.Theﬁrst

term giving a non-vanishing contribution to (23.27)is

V  R

−3

[(r

· r

) − 3(r

· n)(r

· n)], n being the unit

vector in the direction of R. Substituted into (23.26),

this potential leads to the expression

U(R) =−

(23.28)

for the interatomic potential [23.15], where

≈





k,n>F;i, j≤F

|i|r|k|

| j|r|n|

(ε

+ ε

− ε

)

(23.29)

Calculations [23.16] show that the inclusion of

higher-order corrections is important for obtaining ac-

curate values for ∆E

corr

and C

. However, to improve

accuracy by taking into account the corrections to dia-

grams (23.26) requires considerable effort. Indeed, there

are several types of corrections to (23.26)suchas(i)

screening of the Coulomb interelectron interaction by

the electron–vacancy excitations; (ii) interaction be-

tween vacancies ij ; (iii) interaction between electrons

and vacancies ki(nj)(kj(ni)); and (iv) interaction be-

tween electrons kn. Corrections to the HF ﬁeld itself

which acts upon electrons k, n and vacancies i, j are

discussed in Sect. 23.2.3.

Screening of the Coulomb interelectron interaction

is very important, and in many cases must be taken into

account non-perturbative. The simplest way to do this

is to use RPA, which deﬁnes the effective interelectron

interaction

Γ as a solution of an integral equation, shown

diagrammatically by

(23.30)

If V in (23.27) is replaced by

Γ , an expression for ∆E

corr

in RPA can be derived.

Exchange is very important in atoms and molecules,

so diagram (23.30) can be modiﬁed to include this

effect, thus leading to the effective interaction Γ in

RPAE [23.12, 13, 16]:

(23.31)

Replacing V in (23.27)byΓ gives a rather accurate

expression for ∆E

corr

in RPAE. Taking into account

Part B 23.2

366 Part B Atoms

screening also affects the long-range interatomic in-

teraction considerably by altering the constant C

in (23.28).

The ground state energy of an atom or molecule is

modiﬁed by an external ﬁeld. For a not too intense elec-

tromagnetic ﬁeld, the simplest correction to the ground

state energy is given by the diagrams

(23.32)

Considering a dipole external ﬁeld, its interaction with

the atomic electrons is given by W =



i≤F

E· r

, E be-

ing the strength of the ﬁeld. The ground state energy

shift is given by ∆E =−α(ω)E

/2, where α(ω) is the

dynamical dipole polarizability and ω is the frequency

of the ﬁeld. According to (23.32), α(ω) is determined

α(ω) =





k>F;i≤F

2|i|z|k|

(ε

− ε

)

(ε

− ε

)

− ω

, (23.33)

where z is a component of the vector r.

RPAE corrections to α(ω) are discussed in

Sect. 23.2.5 in connection with the photoionization

process.

Non-dipole polarizabilities of other multipolarities

can be obtained in the lowest order of interelectron

interaction using (23.32) with a properly chosen interac-

tion operator between the electromagnetic ﬁeld and an

electron, instead of W =



i≤F

E· r

23.2.2 Characteristics of One-Particle States

A single vacancy or electron can propagate from one in-

stant of interaction to another, as described to zero order

by elements (23.1b) [or (23.1a)] with dots (23.1f) atthe

ends. This line represents an HF one-particle state with

a given angular momentum, spin, and total momentum.

Accounting for virtual or real atomic excitations leads,

for a vacancy, to a diagram similar to (23.25) but with

oppositely directed arrows. Because the interaction with

these excitations is usually much smaller than the en-

ergy distance between shells, in the sum over q only the

term q = i, i being the considered vacancy state, need be

taken into account. Interaction with the vacuum leaves

the angular momentum, spin,and total momentum un-

altered. It can however change the energy, and lead to

a ﬁnite lifetime for a vacancy state.

Analytically, the vacancy propagation in the HF ap-

proximation is described by the one-particle HF Green’s

function G

(E) = 1/(ε

− E). (23.34)

Solving (23.25) for a vacancy i with only Σ

terms

included gives

(E) = 1/[ε

+ Σ

(E) − E] . (23.35)

The pole in G(E) which determines the vacancy energy

is shifted from E = ε

to E

= ε

+ Σ

). The quan-

tity Σ

(E) is called the self-energy, and is in general

a complex function of energy, its imaginary part deter-

mining the lifetime of the vacancy i. Near E

,(23.35)

can be written in the form

(E) ≈ F

[

+ Σ

) − E

]

= F

/(E

− E),

(23.36)

where



1 −

∂Σ

(E)

∂E



E=E



−1

(23.37)

is called the spectroscopic factor. It characterizes the

probability for more complicated conﬁgurations to be

admixed into a single vacancy state i [23.12].

An important problem is to calculate the self-energy

part Σ(E). The ﬁrst nonzero contributions are

a) b)

i' j' i i' i

exchange

terms.

(23.38)

Speciﬁc calculations [23.16] demonstrate that if the in-

termediate electron states n [in (23.38a)] and kn [in

(23.38b)] are found in the ﬁeld of vacancies jj



and ii



the diagrams (23.38) are able to reproduce the values

of the correlation energy shift with about 5% accuracy.

For outer subshell vacancies, the contributions (23.38a)

and (23.38b) are almost equally important, to a large ex-

tent cancelling each other. For example, (23.38a) shifts

the outer 3p vacancy in Ar to lower binding ener-

gies by 0.1 Ry, while the contribution of (23.38b) is

−0.074 Ry. The total value 0.026 Ry is small and close

to the experimental one, which is 0.01 Ry. For inner va-

cancies, (23.38a) is dominant because the intermediate

states in (23.38b) have large virtualities and are therefore

small. The main contribution to the sum over j



comes

from the term j



= i



= i, which gives for the energy

Part B 23.2

Many-Body Theory of Atomic Structure and Processes 23.2 Calculation of Atomic Properties 367

shift of level i

∆ε

= Σ

(2)

(ε

) =





n>F; j≤F

|n|r

−1

| j|

− ε

. (23.39)

The value (23.39) is positive. Most important higher-

order corrections will be included if V in (23.38a) is

replaced by Γ from (23.31).

The physical meaning of diagram (23.38a) is trans-

parent: it accounts for conﬁguration mixing of one

vacancy i and “two vacancies jj



– one electron n” states

in the lowest order in the interelectron interaction. Dia-

gram (23.38b) is not as transparent, and for i = i



its

intermediate state appears to violate the Pauli principle.

However, as noted in connection with (23.14), the Pauli

principle should not be considered as a restriction in

constructing intermediate states.

Diagram (23.38a) and its exchange can have an

imaginary part, which gives the probability of Auger

decay γ

(A)

, calculated to the lowest order in the inter-

electron interaction. For (23.38a) one has

(A)

= Im

[

)

]

=2π





j, j



≤F;n>F

|in|V| jj



|

δ(ε

+ ε



− ε

(23.40)

The width γ

(A)

is usually much smaller than

Re[Σ

)], but there are several exceptional cases with

abnormally large Auger widths, among which the most

impressive is the 4p-vacancy in Xe with its γ

≈ 10 eV.

Higher-order corrections include those which are

taken into account when V in (23.40) is replaced by Γ

from (23.31). The others include jj



vacancy–vacancy

interaction, the interaction between vacancies jj



and the

electron n and so on. As noted above, all of these can

be obtained step by step by inserting the elements (23.4)

into (23.38). To select the most important corrections,

a physical idea and/or experience are necessary. For in-

stance, if the energy transferred in the decay process

∆ε = ε



− ε

is close to some threshold energies of

atomic intermediate or outer shells, corrections which

include virtual excitation of this shell must be taken into

account.

The contribution to the spectroscopic factor

from (23.38a) is given according to (23.37)by

(2)

≡







1 +





j, j



≤F;n>F

|in|V| j



j|

(ε

+ ε



− ε

)







−1

(23.41)

Generally, for any Fermi particle, F

≤ 1 [23.17] because

there cannot be more than one particle in a given state.

Note that the integrand in (23.41) is the lowest-order

admixture of the jj



n state to a pure one-vacancy state i.

AsmallF value means strong mixing. For atoms, F

usually close to 1, but there are exceptions where F is

small. For example, F

in Xe is about 0.33 [23.12].

The operator Σ

ij(n)

(ε) has non-diagonal matrix

elements, which leads to admixture of other one-

vacancy j or one-electron n states to the vacancy i.

A measure of this admixture is given by the ratio

ij(n)

(ε

)/(ε

j(n)

− ε

In higher orders, decay processes more complex than

those described by the imaginary part of (23.38a) be-

come possible. For example, this could be a two-electron

Auger decay in which the transition energy is distributed

between two outgoing electrons. An example of the

lowest-order diagram for this process is

(23.42)

This is one of those diagrams which describe the mix-

ing of a pure one-vacancy state with a quite complex

conﬁguration jj

23.2.3 Electron Scattering

Propagationofanelectroninadiscretelevelor

in a scattering state can be described in the same

way as for a vacancy. The electron wave function

is determined by (23.25). Using the correspondence

rule (23.14), (23.25) can be expressed analytically in

the form



−

∇

−



i≤F



−r|





)



− ε



(r)



i≤F



−r|

∗



)ψ



)φ

(r)



Σ(r, r



, ε)ψ



)dr



(23.43)

The terms with the Coulomb interelectron interaction



− r|

−1

determine the Hartree–Fock self-consistent

potential. The last term in (23.43) represents the nonlocal

energy dependent polarization interaction of the contin-

uous spectrum electron with the target atom. Although

Part B 23.2