Drake G.W.F. (editor) Handbook of Atomic, Molecular, and Optical Physics

Подождите немного. Документ загружается.

1190 Part F Quantum Optics

laser

KDP

Idler

Signal

Beam dump

Fixed QWP

Rotatable QWP

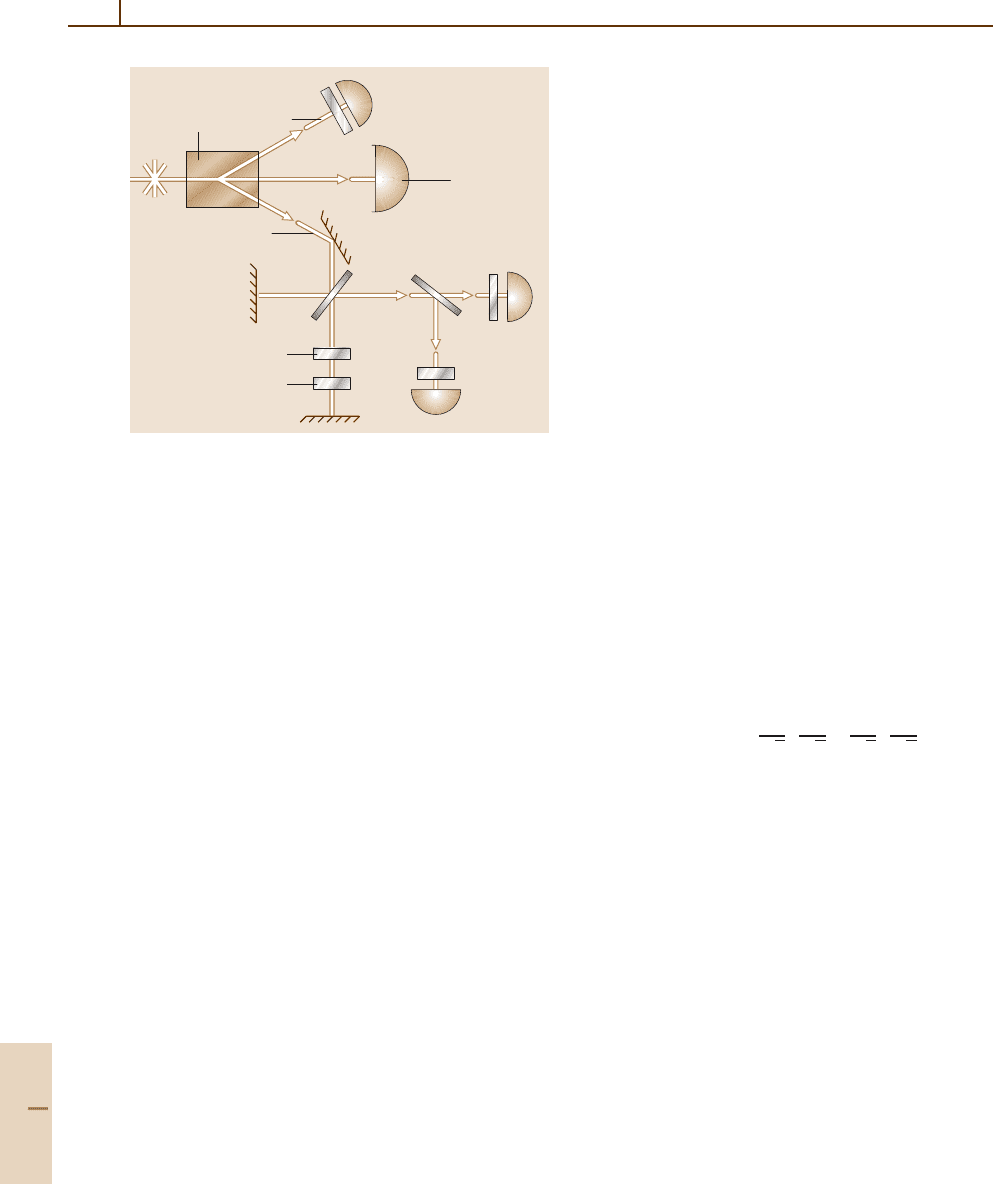
Fig. 80.3 The energy–time uncertainty relation and wave

function collapse were studied by investigating the effect

of various ﬁlters before the detectors in a single-photon

interference experiment [80.5, 81]

there was no trigger, no fringes were observed, imply-

ing a much shorter wave packet. This is a nonlocal effect

in that the photons could in principle be arbitrarily far

away from each other when the collapse occurs.

80.3.3 Two-Photon Interference

In the above experiments, interference occurs between

two paths taken by a single photon. An early experi-

ment to demonstrate two-photon interference using the

down-conversion light source was performed by Ghosh

and Mandel [80.85]. They looked at the counting rate

of a detector illuminated by both of the twin beams.

No interference was observed at the detector, because

although the sum of the phases of the two beams emit-

ted in parametric ﬂuorescence is well deﬁned (by the

phase of the pump), their difference is not, due to the

number-phase uncertainty principle. However, the rate

of coincidence detections between two such detectors

whose separation was varied did display high-visibility

interference fringes. Whereas in the standard two-slit

experiment, interference occurs between the two paths

a single photon could have taken to reach a given point

on a screen, in this case it occurs between the possibility

that the signal photon reached detector 1 and the idler

photon detector 2, and the possibility that the reverse

happened. This experiment provides a manifestation of

quantum nonlocality; interference occurs between al-

ternate global histories of a system, not between local

ﬁelds. At a null of the coincidence fringes, the detection

of one photon at detector 1 excludes the possibility of

ﬁnding the conjugate photon at detector 2.

Such interference becomes clearer in the related

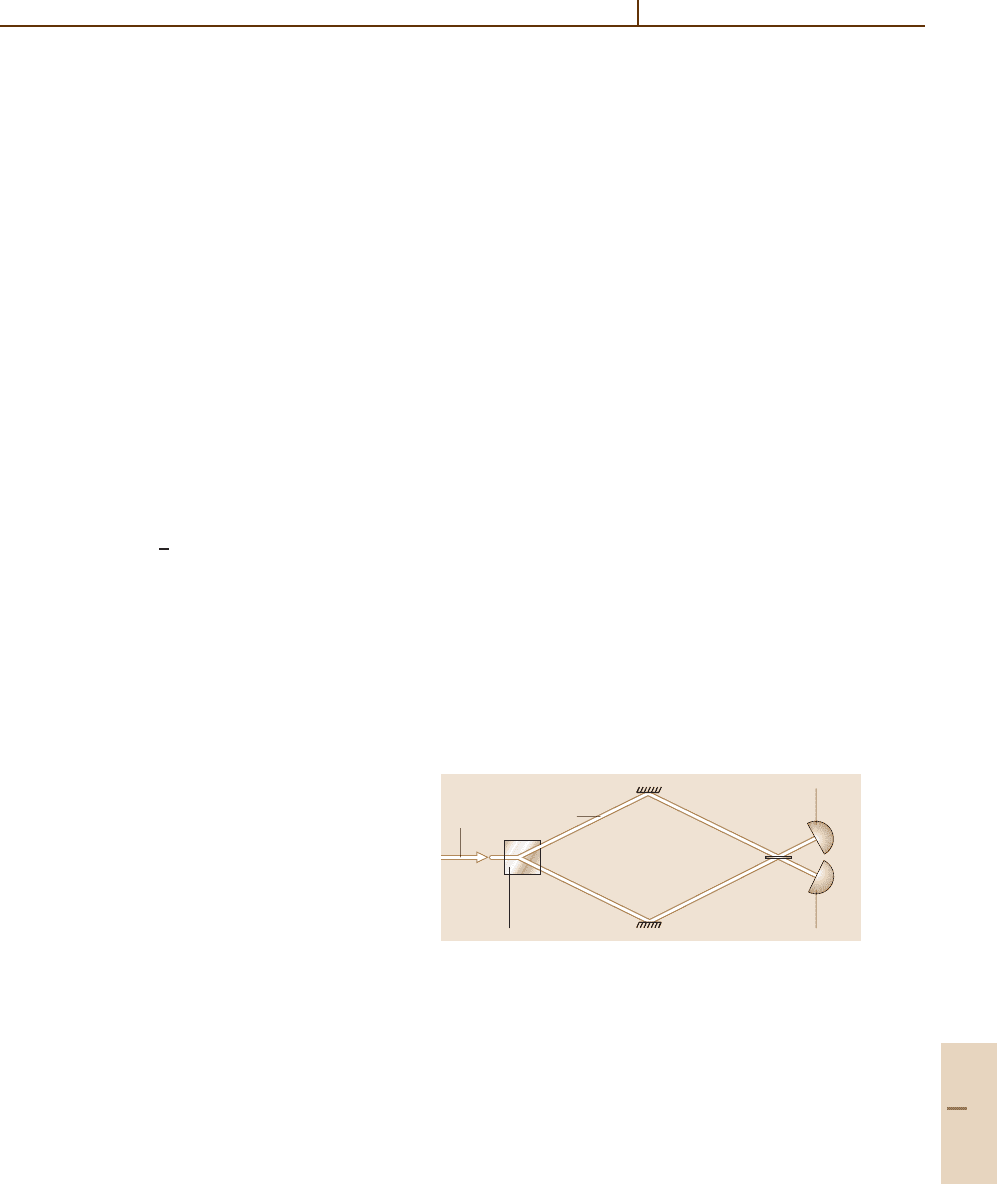
interferometer of Hong et al. [80.86](Fig.80.4). The

identically polarized conjugate photons from a down-

conversion crystal are directed to opposite sides of

a 50–50 beam splitter, such that the transmitted and

reﬂected modes overlap. If the difference in the path

lengths ∆L prior to the beam splitter is larger than

the two-photon correlation length (of the order of the

coherence length of the down-converted light), the pho-

tons behave independently at the beam splitter, and

coincidence counts between detectors in the two out-

put ports are observed half of the time – the other

half of the time both photons travel to the same de-

tector. However, when ∆L ≈ 0, such that the photon

wave packets overlap at the beam splitter, the probabil-

ity of coincidences is reduced, in principle to zero if

∆L = 0. One can explain the coincidence null at zero

path-length difference using the Feynman rules for cal-

culating probabilities: add the probability amplitudes of

indistinguishable processes which lead to the same ﬁ-

nal outcome, and then take the absolute square. The two

indistinguishable processes here are both photons being

reﬂected at the beam splitter (with Feynman amplitude

r ·r) and both photons being transmitted (with Feyn-

man amplitude t ·t). The probability of a coincidence

detection is then

=|r ·r +t ·t|



√



= 0 ,

(80.6)

assuming a real transmission amplitude, and where the

factors of i come from the phase shift upon reﬂection at

a beam splitter [80.87, 88].

The possibility of a perfect null at the center

of the dip is indicative of a nonclassical effect. In-

deed, classical ﬁeld predictions allow a maximum

coincidence-fringe visibility of only 50% [80.89].

The tendency of the photons to travel off together

at the beam splitter can be thought of as a man-

ifestation of the Bose–Einstein statistics for the

photons [80.90]. In practice, the bandwidth of the pho-

tons, and hence the width of the null, is determined

by ﬁlters and/or irises before the detectors [80.82].

Widths as small as 5 µm have been observed, cor-

responding to time delays of only 15 fs [80.91].

Consequently, one application is the determination of

single-photon propagation times with extremely high

time resolution (Sect. 80.8).

Part F 80.3

Quantum Optical Tests of the Foundations of Physics 80.4 Complementarity and Coherence 1191

80.4 Complementarity and Coherence

80.4.1 Wave–Particle Duality

The complementary nature of wave-like and particle-

like behavior is frequently interpreted as follows: due

to the uncertainty principle, any attempt to measure the

position (particle aspect) of a quantum leads to an un-

controllable, irreversible disturbance in its momentum,

thereby washing out any interference pattern (wave as-

pect) [80.93, 94]. This picture is incomplete though; no

“state reduction,” or “collapse,” is necessary to destroy

interference, and measurements which do not involve

reduction can be reversible. One must view the loss

of coherence as arising from an entanglement of the

system wave function with that of the measuring ap-

paratus (MA) [80.95]. Previously interfering paths can

thereby become distinguishable, such that no interfer-

ence is observed. Consider the simplest experiment,

a Mach–Zehnder interferometer with a 90

◦

polariza-

tion rotator in arm 1. If horizontally polarized light is

input, the state before the recombining beam splitter is



|1|V +|2|H)/

√



,where|1 and |2 indicate the

path of the photon. Because the polarization – playing

the role of the MA – labels the path, no interference is

observed at the output. Englert [80.96] has introduced

a generalized relation quantifying the interplay between

the wave-like attributes of a system (as measured by the

fringe visibility V) and the particle-like character (as

measured by the distinguishability D of the underlying

quantum processes):

+ D

≤ 1 . (80.7)

The equality holds for pure input states. This rela-

tion has now been well veriﬁed in optical systems

like that described above [80.97, 98], as well as in

atom interferometry (Sect. 77.6) [80.99]. In the latter,

the role of the polarization was played by internal en-

ergy states of an atom diffracted off a standing light

wave.

80.4.2 Quantum Eraser

The interference lost to entanglement may be re-

gained if one manages to “erase” the distinguishing

information. This is the physical content of quantum

erasure [80.100, 101]. The primary lesson is that one

must consider the total physical state, including any

MA with which the interfering quantum has become

entangled, even if that MA does not allow access-

ible which-path information [80.102]. If the coherence

of the MA is maintained, then interference may be

recovered.

The ﬁrst demonstration of a quantum eraser was

based on the interferometer in Fig. 80.4 [80.92]. A half

waveplate inserted into one of the paths before the

beam splitter serves to rotate the polarization of light

in that path. In the extreme case, the polarization is

made orthogonal to that in the other arm, and the r·r

and t·t processes become distinguishable; hence, the de-

structive interference which led to a coincidence null

does not occur. The distinguishability can be erased,

however, by using polarizers just before the detectors.

In particular, if the initial polarization of the pho-

tons is horizontal, and the waveplate rotates one of

the photon polarizations to vertical, then polarizers at

◦

before both detectors restore the original interfer-

ence dip. If one polarizer is at 45

◦

and the other at

−45

◦

, interference is once again seen, but now in the

form of a peak instead of a dip (Fig. 80.5). There are

four basic measurements possible on the MA (here the

polarization) – two of which yield which-path infor-

mation, one of which recovers the initial interference

fringes (here the coincidence dip), and one of which

yields interference anti-fringes (the peak instead of the

dip). In some implementations, the decision to mea-

sure wave-like or particle-like behavior may even be

delayed until after detection of the original quantum,

an irreversible process [80.103–105]. (This is an ex-

tension of the original delayed-choice discussion by

Nonlinear

crystal

Fig. 80.4 Simpliﬁed setup for a Hong–Ou–Mandel (HOM)

interferometer [80.86]. Coincidences may result from both

photons being reﬂected, or both being transmitted. When

the path lengths to the beam splitter are equal, these

processes destructively interfere, causing a null in the co-

incidence rate. In a modiﬁed scheme, a half waveplate in

one arm of the interferometer (at “A”) serves to distin-

guish these otherwise interfering processes, so that no null

in coincidences is observed. Using polarizers before the

detectors, one can “erase” the distinguishability, thereby

restoring interference [80.92] (Sects. 80.4.2 and 80.6.2)

Part F 80.4

1192 Part F Quantum Optics

450

400

350

300

250

200

150

100

–1110

–1090 –1070 –1050 –1030 –990–1010

Trombone prism position (µm)

Coincidence rate (s

–1

)

45°, 45°

Theory

45°, 22°

Theory

45°, –45°

Theory

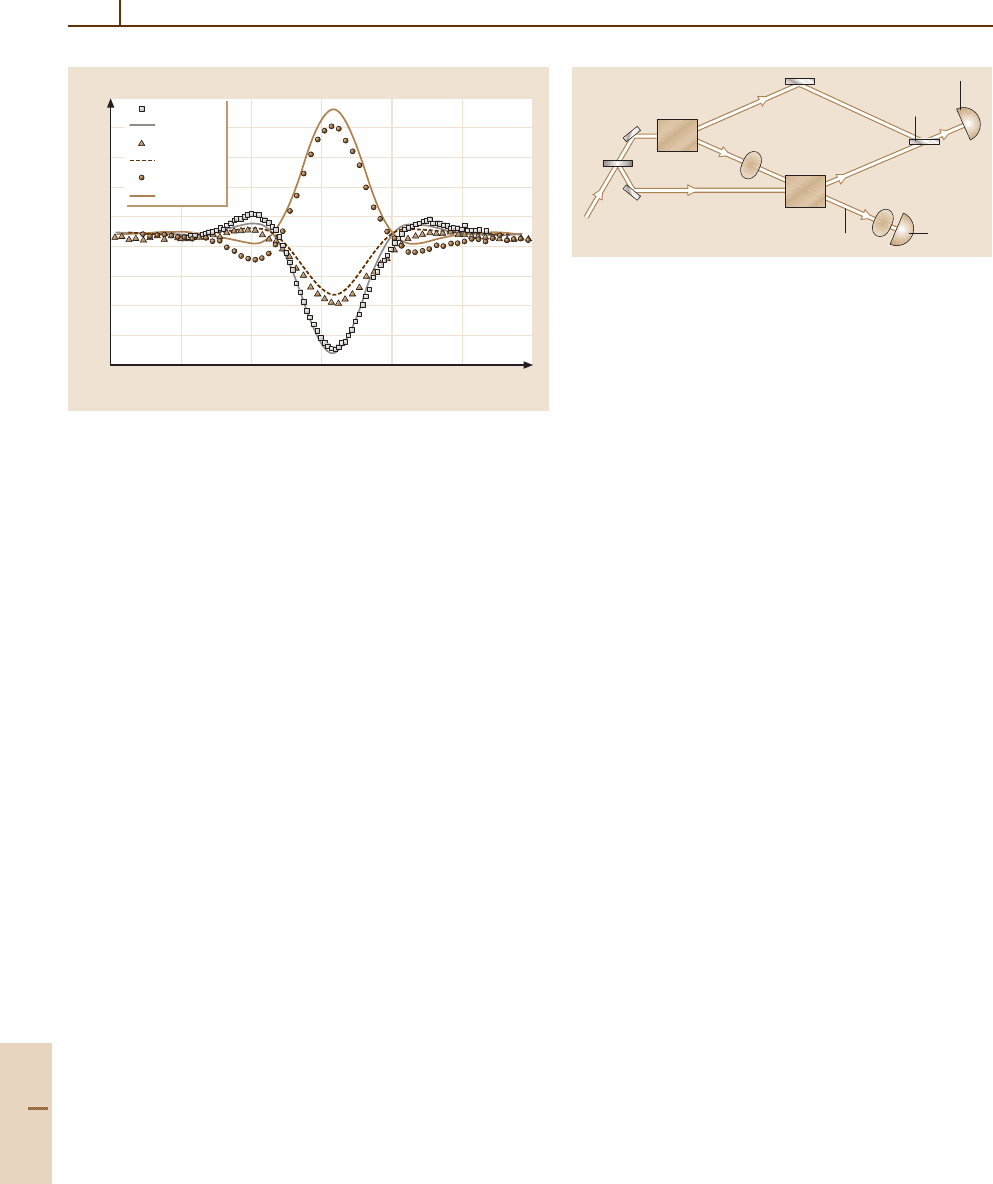
Fig. 80.5 Experimental data and scaled theoretical curves (adjusted

to ﬁt observed visibility of 91%) with polarizer 1 at 45

◦

and polar-

izer 2 at various angles. Far from the dip, there is no interference

and the angle is irrelevant [80.92]

Wheeler [80.106], and the experiments by Hellmuth

et al. and Alley et al. [80.107,108], in which the decision

to display wave-like or particle-like aspects in a light

beam may be delayed until after the beam has been split

by the appropriate optics.) But in all cases, one must

correlate the results of measurements on the MA with

the detection of the originally interfering system. This

requirement precludes any possibility for superluminal

signaling.

In a related atom-optics experiment, researchers ob-

served contrast loss in an atom interferometer when

single photons were scattered off the atoms (yielding

which-path information) [80.110]. They further demon-

strated that the lost coherence could be recovered by

observing only atoms that were correlated with photons

emitted into a limited angular range, in essence realizing

a quantum eraser.

80.4.3 Vacuum-Induced Coherence

A somewhat different demonstration [80.109, 111]of

complementarity involves two down-conversion crys-

tals, NL1 and NL2, aligned such that the trajectories of

the idler photons from each crystal overlap (Fig. 80.6).

A beam splitter acts to mix the signal modes. If the

path lengths are adjusted correctly, and the idler beams

overlap precisely, there is no way to tell, even in prin-

ciple, from which crystal a photon detected at D

originated. Interference appears in the signal singles

rate at D

, as any of the path lengths is varied. If the

NL1

NL2

, i

Fig. 80.6 Schematic of setup used in [80.109]. The idler

photons from the two crystals are indistinguishable; conse-

quently, interference fringes may be observed in the signal

singles rate at detector D

. Additional elements at A and B

can be used to make a quantum eraser

idler beam from crystal NL1 is prevented from enter-

ing crystal NL2, then the interference vanishes, because

the presence or absence of an idler photon at D

then

“labels” the parent crystal. One explanation for the

effect of blocking this path is that coherence is es-

tablished by the idler-mode vacuum ﬁeld seen by both

crystals.

Experiments have also been performed in which

a time-dependent gate is introduced in the idler arm

between the two crystals [80.112]. As one expects, the

presence or absence of interference depends on the ear-

lier state of the gate, at the time when the idler photon

amplitude was passing through it.

80.4.4 Suppression

of Spontaneous Down-Conversion

A modiﬁcation [80.113] of this two-crystal experiment

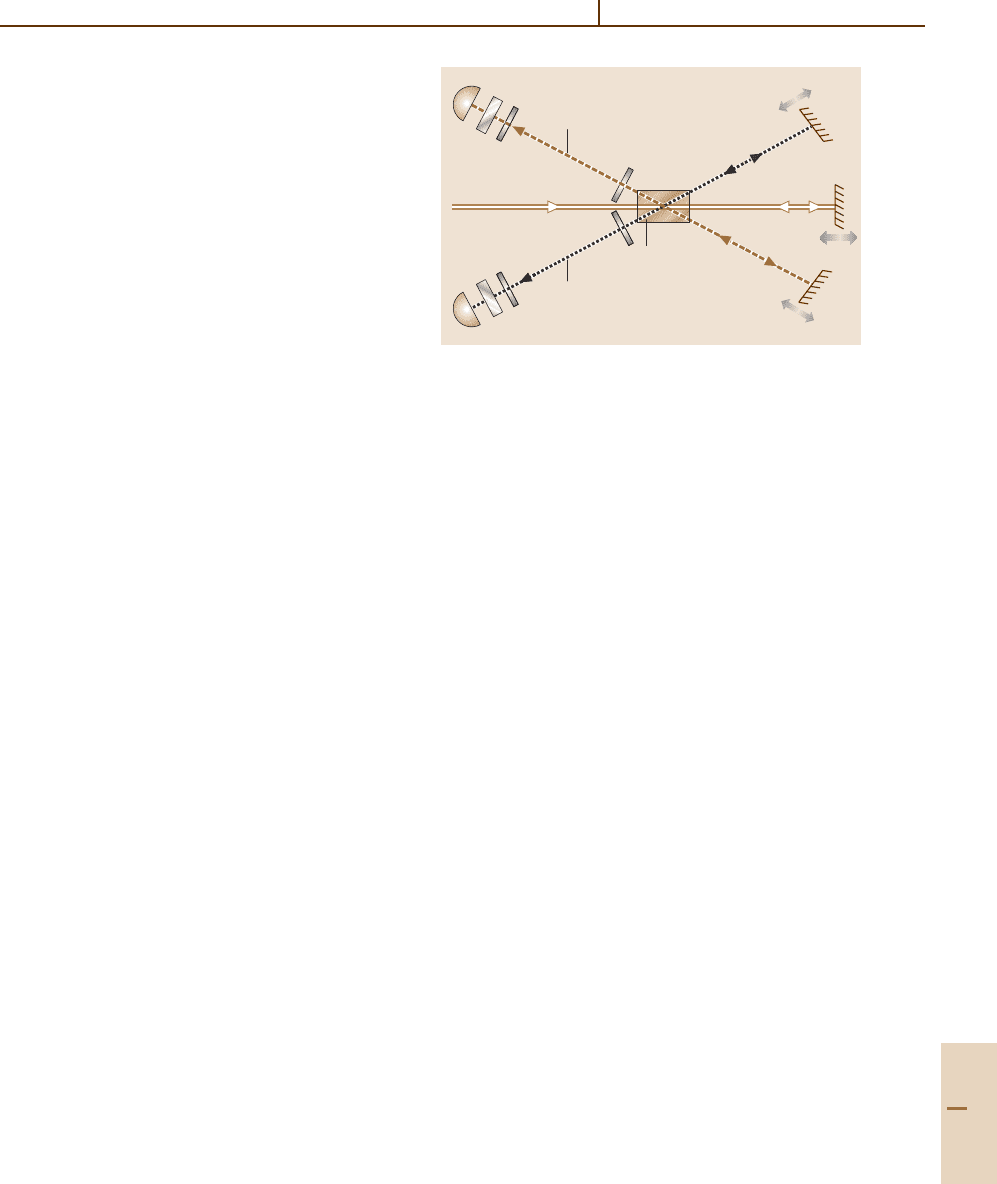
uses only a single nonlinear crystal (Fig. 80.7). A given

pump photon may down-convert in its initial right-ward

passage through the crystal, or in its left-going return

trip (or not at all, the most likely outcome). As in the

previous experiment, the idler modes from these two

processes are made to overlap; moreover, the signal

modes are also aligned to overlap. Thus, the left-going

and right-going production processes are indistinguish-

able and interfere. The result is that fringes are observed

in all of the counting rates (i. e., the coincidence rate

and both singles rates) as any of the mirrors is trans-

lated. A different interpretation is as a change in the

spontaneous emission of the down-converted photons,

akin to the suppression of spontaneous emission in cav-

ity QED demonstrations, discussed in Sects 80.2.1 and

79.2. Subsequent theoretical and experimental work has

shown that, in a sense, there are always photons be-

tween the down-conversion crystal and the mirrors, even

Part F 80.4

Quantum Optical Tests of the Foundations of Physics 80.5 Measurements in Quantum Mechanics 1193

in the case of complete suppression of the spontaneous

emission process [80.114, 115]. This same conclusion

should also apply in the atom case [80.116], though

in contrast to that system, for the down-conversion ex-

periment the distances to the mirrors are much longer

than the coherence lengths of the spontaneously emitted

photons.

One recent application of this phenomenon is to

study effective nonlinearities at the single-photon level,

which has enabled the construction of a 2-photon

switch [80.117]. Finally, with the inclusion of wave-

plates to label the photons’ paths, and polarizers to

erase this information, an improved quantum eraser ex-

periment was also completed, in which the which-path

information for one photon was carried by the other

photon [80.104].

Pump

Signal

Idler

LiIO

Fig. 80.7 Schematic of the experiment to demonstrate

enhancement and suppression of spontaneous down-

conversion [80.113]

80.5 Measurements in Quantum Mechanics

80.5.1 Quantum (Anti-)Zeno Effect

A strong measurement of a quantum system will project

it into one of its eigenstates [80.95]. If the system evolves

slowly out of its initial state: |Ψ(t = 0)= |Ψ

→

(1 −t

/τ

)

1/2

|Ψ

+t/τ|Ψ

, then repeated measure-

ments with an interval much less than τ can inhibit this

evolution. If there are N total measurements within τ,

then the probability for the system to still be in the ini-

tial state is P(τ) =



1 −(τ/N )

/τ



→ 1asN →∞.

This phenomenon, known as the quantum Zeno ef-

fect [80.118], has been experimentally observed using

3levelsin

ions [80.119]. The ions were prepared

in state |i, and weakly coupled to state | f  via RF ra-

diation that induced a slow Rabi oscillation between

the two states. Thus, in the absence of any interven-

ing measurements, the ions evolved sinusoidally into

state | f . When rapid measurements were made (by

a laser strongly coupling state | f  to readout state |r,

hence leading to strong ﬂuorescence only if the atom was

in state | f ), the effect was to inhibit the |i→|f  tran-

sition. Note that here it was the absence of ﬂuorescent

photons which projected the state at each measurement

back into the state |i (Sect. 80.5.3). Also, although we

have explained the effect in terms of a repeated “col-

lapse” of the wave function back into its initial state,

equally valid explanations without such reductions are

also possible [80.120, 121].

Koffman and Kurizki have pointed out that the

above inhibition phenomenon depends on there being

a bounded number of ﬁnal states (the ion example had

only one). If instead the measurement process actu-

ally increases the number of accessible ﬁnal states | f ,

then one obtains the “anti-Zeno” effect, in which the

|i→|f  rate is enhanced rather than suppressed by fre-

quent measurements [80.122]. For example, this would

be the case in the ion example if the |i→|f  transition

were spontaneous (allowing all frequencies) instead of

driven (proceeding only at the driving Rabi frequency).

The anti-Zeno effect has been observed by monitoring

the survival time (against tunneling escape) of atoms

trapped in an accelerating far-detuned standing wave of

light [80.123].

80.5.2 Quantum Nondemolition

The uncertainty principle between the number of

quanta N and phase φ of a beam of light,

∆N∆φ ≥1/2 ,

(80.8)

implies that to know the number of photons exactly,

one must give up all knowledge of the phase of the

wave. In theory, a quantum nondemolition (QND)pro-

cess is possible [80.124]: without annihilating any of

the light quanta, one can count them. It might seem

that this would make possible successive measurements

on noncommuting observables of a single photon, in

violation of the uncertainty principle; it is the unavoid-

able introduction of phase uncertainty by any number

measurement which prevents this.

QND schemes [80.125] often employ the intensity-

dependent index of refraction arising from the optical

Part F 80.5

1194 Part F Quantum Optics

Kerr effect (Sect. 72.4.2) – the change in the index due

to the intensity of the “signal” beam changes the opti-

cal phase shift on a “probe” beam [80.126–128]. Other

proposals include using the Aharonov–Bohm effect to

sense photons via the phase shift their ﬁelds induce in

passing electrons [80.129, 130]. To date the closest ex-

perimental realization [80.26]ofaQND measurement

– of the photon number in a microwave cavity – was

performed by passing Rydberg atoms [80.131, 132]in

a superposition of the ground and excited states through

the cavity. The interaction with the cavity photon is ad-

justed to be equivalent to a 2 π-pulse (Sect. 79.5). The

result is that in the absence of any photon, the quantum

state of the atoms after the cavity was unchanged; with

a photon in the cavity, the ground state acquired an extra

relative phase of π, which was then detected by measur-

ing the atom’s quantum state. An efﬁciency approaching

50% was achieved. Recently, it was suggested that opti-

cal QND measurements could enable scalable quantum

computing [80.133].

80.5.3 Quantum Interrogation

The previous section described techniques to measure

the presence of a photon without absorbing it. Now we

discuss a method – quantum interrogation – to optically

detect the presence of an object without absorbing or

scattering a photon. The possibility that the absence of

a detection event – a “negative-result” measurement –

can lead to wavepacket reduction was ﬁrst discussed by

Renninger [80.134] and later by Dicke [80.135]. Here we

consider the Gedankenexperiment proposed by Elitzur

and Va i d man (EV), a simple single-particle interferom-

eter, with particles injected one at a time [80.136]. The

path lengths are adjusted so that all the particles leave

a given output port (A), and never the other (B). Now

suppose that a nontransmitting object is inserted into one

of the interferometer’s two arms – to emphasize the re-

sult, EV considered an inﬁnitely sensitive “bomb”, such

that interaction with even a single photon would cause it

to explode. By classical intuition, any attempt to check

for the presence of the bomb involves interacting with

it in some way, and, by hypothesis, inevitably setting it

off.

Quantum mechanics, however, allows one to be cer-

tain some fraction of the time that the bomb is in place,

without setting it off. After the ﬁrst beam splitter of

the interferometer, a photon has a 50% chance of head-

ing towards the bomb, and thus exploding it. On the

other hand, if the photon takes the path without the

bomb, there is no more interference, since the nonex-

plosion of the bomb provides welcher Weg (“which

way”) information (see Sect. 80.4.1). Thus the photon

reaches the ﬁnal beam splitter and chooses randomly

between the two exit ports. Some of the time (25%), it

leaves by output port B, something which never hap-

pened in the absence of the bomb. This immediately

implies that the bomb (or some nontransmitting object)

is in place – even though (since the bomb is unexploded)

it has not interacted with any photon; EV termed this

an “interaction-free measurement”. (We prefer the more

general description “quantum interrogation”, which then

includes cases – e.g., detecting a semi-transparent or

quantum object – where it may not be possible to logi-

cally exclude the possibility of an interaction.) It is the

mere possibility that the bomb could have interacted

with a photon which destroys interference. An initial

experimental implementation of these ideas [80.137]

used down-conversion to prepare the single photon states

(Sect. 80.1), and a single-photon detector as the “bomb”.

Subsequently the technique was implemented incorpo-

rating focusing lenses, which would enable the image

(more correctly, the silhouette) of an object to be de-

termined with less than one photon per “pixel” being

absorbed [80.138].

By adjusting the beamsplitter reﬂectivities in the

above example, one can achieve at most a 50% frac-

tion of measurements that are interaction-free. An

improved method, relying on the quantum Zeno ef-

fect [80.118] (Sect. 80.5.1), was discovered with which

one can in principle make this fraction arbitrarily close

to 1 [80.137]. For example, consider a photon initially

in cavity #1 of two identical cavities coupled by a loss-

less beam splitter whose reﬂectivity R = cos

(π/2N ).

If the photon’s coherence length is shorter than the cav-

ity length, after N cycles the photon will with certainty

be located in cavity #2, due to an interference effect (the

equivalent of a π-pulse interaction). However, if cav-

ity #2 instead contains an absorbing object (e.g., the

ultra-sensitive bomb), at each cycle there is only a small

chance (= 1 − R) that the photon will be absorbed; oth-

erwise, the non absorption projects the photon wave

packet entirely back onto cavity #1. After all N cycles,

the total probability for the photon to be absorbed by the

object is 1 − R

, which goes to 0 as N becomes large.

(In practice, unavoidable losses in the system limit the

maximum number of cycles and hence the achievable

performance [80.139].) The photon effectively becomes

trapped in cavity #1, thus indicating umambiguously the

presence of the object in cavity #2.

This quantum-Zeno version of interrogation was

ﬁrst implemented using the inhibited rotation of a pho-

Part F 80.5

Quantum Optical Tests of the Foundations of Physics 80.6 The EPR Paradox and Bell’s Inequalities 1195

ton’s polarization (the object to be detected blocked

one arm of a polarizing interferometer through which

the photon was repeatedly cycled), achieving an efﬁ-

ciency of 75% [80.139]. A cavity-based implementation,

in which the presence of the absorbing object inside

a high-ﬁnesse cavity vastly increased the reﬂection off

the cavity [80.140], detected the presence of the object

with only 0.15 photons on average being absorbed or

scattered [80.141].

80.5.4 Weak and “Protected”

Measurements

Aharonov, Albert,andVa idma n extended quantum mea-

surement theory by introducing “weak” measurement,

a procedure that determines a physical property of

a quantum system belonging to an ensemble that is

both preselected and postselected [80.142, 143]. In the

standard theory, a quantum system is measured by

entangling its eigenstates with distinguishable pointer

states of a measurement device, completely resolving

the observable eigenvalue spectrum. The measure-

ment can be weakened by increasing the overlap of

the pointer states, consequently reducing the resolu-

tion of the eigenstates. When performed between two

measurements this can give surprising results – in

contrast to ordinary expectation values, the pointer

can lie outside the range of the eigenvalue spec-

trum of the measured observable O. The “weak

value” O

≡Ψ

ini

|O|Ψ

ﬁn

/Ψ

ﬁn

|Ψ

ini

 between prese-

lected (|Ψ

ini

) and postselected (|Ψ

ﬁn

) states completely

characterizes the outcome of the weak measurement.

Weak measurements do not disturb each other, so that

the weak values of non-commuting observables can

be measured simultaneously [80.144, 145]. Further-

more, they have proved to yield meaningful results in

many different circumstances, e.g., Hardy’s paradox of

Sect. 80.6.5 [80.146], measurement of negative kinetic

energies [80.147], and the “observation” of a single

particle in two locations [80.148]. One other poten-

tially powerful application of weak measurements is the

ampliﬁcation of weak signals, which was ﬁrst demon-

strated by amplifying the birefringence-induced small

displacement of optical ﬁelds [80.149, 150]. It was re-

cently shown that weak measurements of this kind in

fact arise naturally in ﬁber optics telecom networks,

due to polarization-mode dispersion and polarization-

dependent losses [80.151]. One recent proposal [80.152]

suggests that the controversy over whether or not

“welcher Weg” information may be obtained (and in-

terference consequently destroyed) without disturbing

a particle’s momentum (Sect. 80.4.2) may be resolved

by making weak measurements of momentum inside an

interferometer.

The above results push us to reexamine our interpre-

tation of wave functions. We customarily use the wave

function only as a calculational tool, but we have also

learned that it is in some sense physical, and should not

be regarded merely as some distribution from classical

statistics. One proposal [80.153, 154] suggests that the

wave function of a single particle should be regarded as

a real entity. When a state is “protected” from change,

e.g., by an energy gap, and measurements are performed

sufﬁciently “gently”, one should be able to determine not

just the expectation value of position, but the wave func-

tion at many different positions, without altering the state

of the particle. (This idea of measuring the entire wave

function of a single particle should not be conﬂated with

Raymer et al.’s fascinating work on the reconstruction of

the quantum state of a light ﬁeld by repeated sampling

of a large ensemble; see [80.155] and Sect. 78.4.) No

violation of the uncertainty principle or the no-cloning

theorem (Sect. 80.7.1) arises from this, as the ability

to “protect” a state relies on some preexisting knowl-

edge about the state; but it assigns a deeper signiﬁcance

to the wave function, one Aharonov terms “ontolog-

ical,” as opposed to merely epistemological (but see

also [80.156]).

80.6 The EPR Paradox and Bell’s Inequalities

80.6.1 Generalities

Nowhere is the nonlocal character of the quantum

mechanical entangled state as evident as in the “para-

dox” of Einstein, Podolsky,andRosen (EPR) [80.157],

the version of Bohm [80.158], and the related in-

equalities by Bell [80.159, 160]. Consider two photons

traveling off back-to-back, described by the entangled

state

|ψ

−

=

(

, V

−|V

, H



)

√

2 , (80.9)

where the letters denote horizontal (H) or vertical (V)

polarization, and the subscripts denote photon propaga-

tion direction. This state, analogous to the singlet state

of a pair of spin-1/2 particles, is isotropic – it has the

same form regardless of what basis is used to describe

Part F 80.6

1196 Part F Quantum Optics

it. Measurement of any polarization component for one

of the particles will yield a count with 50% probability;

individually, each particle is unpolarized. Nevertheless,

if one measures the polarization component of particle 1

in any basis, one can predict with certainty the po-

larization of particle 2 in the same basis, seemingly

without disturbing it, since it may be arbitrarily remote.

Therefore, according to EPR, to avoid any nonlocal in-

ﬂuences one should ascribe an “element of reality” to

every component of polarization. A quantum mechan-

ical state cannot specify that much information, and is

consequently an incomplete description, according to

the EPR argument. The intuitive explanation implied

by EPR is that the particles leave the source with def-

inite, correlated properties, determined by some local

“hidden variables” not present in quantum mechanics

(QM).

For two entangled particles, a local hidden variable

(LHV) theory can be made which correctly describes

perfect correlations or anti-correlations (i. e., measure-

ments made in the same polarization basis). The choice

of an LHV theory versus QM is then a philosophical

decision, not a physical one. However, in 1964 John

Bell [80.159] discovered that QM gives different statis-

tical predictions than does any LHV theory, for situations

of nonperfect correlations (i. e., analyzers at intermedi-

ate angles). Bell’s inequality (BI) constrains various joint

probabilities given by any local realistic theory, and was

later generalized to include any model incorporating lo-

cality [80.161, 162], and also extended to apply to real

experimental situations [80.163, 164]. With the caveat

of supplementary assumptions (Sect. 80.6.4), Bell’s in-

equalities have now been tested many times, and the vast

majority of experiments have violated them, in support

of QM. One general interpretation is that the predictions

of QM cannot be reproduced by any completely local

theory. It must be that the results of measurements on

one of the particles depend on the results for the other,

and these correlations are not merely due to a common

cause at their creation [80.165, 166].

80.6.2 Polarization-Based Tests

The ﬁrst BI tests were performed with pairs of pho-

tons produced via an atomic cascade, and a later version

incorporated rapid (albeit periodic) switching of the

analyzers [80.167, 168]. Unfortunately, the angular cor-

relation of the cascade photons is not very strong. In

contrast, the strong correlations of the down-converted

photons make them ideal for such tests, the ﬁrst of which

were performed using setups essentially identical to that

already discussed in connection with quantum erasure

(Fig. 80.4). Orthogonally polarized (e.g., horizontal and

vertical) but otherwise identical photons are combined

on a nonpolarizing 50–50 beam splitter. If one consid-

ers only the events with a single photon in each output

(i. e., ignoring the cases for which both photons use the

same beam splitter output port), one obtains the (post-

selected) entangled state (80.9) [80.169, 170]. (In fact,

this technique is now used as a method for characteriz-

ing the indistinguishability of photons from independent

sources, e.g., quantum dots [80.171] or independent

down-conversion crystals [80.172, 173].)

Down-conversion schemes have also been developed

to produce entangled states without the need to post-

select out half of the photons. For example, consider

a type-I phase-matched crystal (Sect. 72.2.2) that down-

converts H-polarized pump photons into V-polarized

pairs; and an adjacent, identical crystal that is rotated

by 90

◦

, thus down-converting V-polarized pump pho-

tons into H-polarized pairs. By coherently pumping

the two crystals with light polarized at |45≡(|V +

|H)/

√

2, one obtains the entangled state (|HH +

|VV /

√

2. (More generally, pumping α|V +e

iϕ

β|H

produces arbitrary nonmaximally entangled states of

the form α|HH+e

iϕ

β|VV [80.174].) Such a source

has produced the largest and fastest violations of Bell

inequalities to date (over 200-σ violation in less than

1 second) [80.175, 176].

Using type-II phase-matching one also can pro-

duce polarization entanglement from a single crys-

tal [80.177]. One member of each down-conversion

pair is emitted along an ordinary polarized cone while

the other is emitted along an extraordinary polarized

cone. If the photons happen to be emitted along the

intersection of the two cones, neither photon will have

a deﬁnite polarization – they will be in the state (|HV +

|VH /

√

2. This entanglement source has now been

used in a variety of quantum investigations, including

Bell inequality tests [80.177, 178], quantum cryptog-

raphy [80.179, 180] (Sect. 80.7.4 and Chapt. 81)and

teleportation [80.181, 182], and as a resource for study-

ing entanglement of more than 2 photons [80.37–42].

80.6.3 Nonpolarization Tests

The advent of parametric down-conversion has also led

to the appearance of several nonpolarization-based BI

tests, using, for example, an entanglement of the pho-

ton momenta (Fig. 80.8) [80.183]. By use of small irises

(labeled ‘A’ in the ﬁgure), Rarity and Tapster examined

four down-conversion modes: 1s, 1i, 2s, and 2i. Beams

Part F 80.6

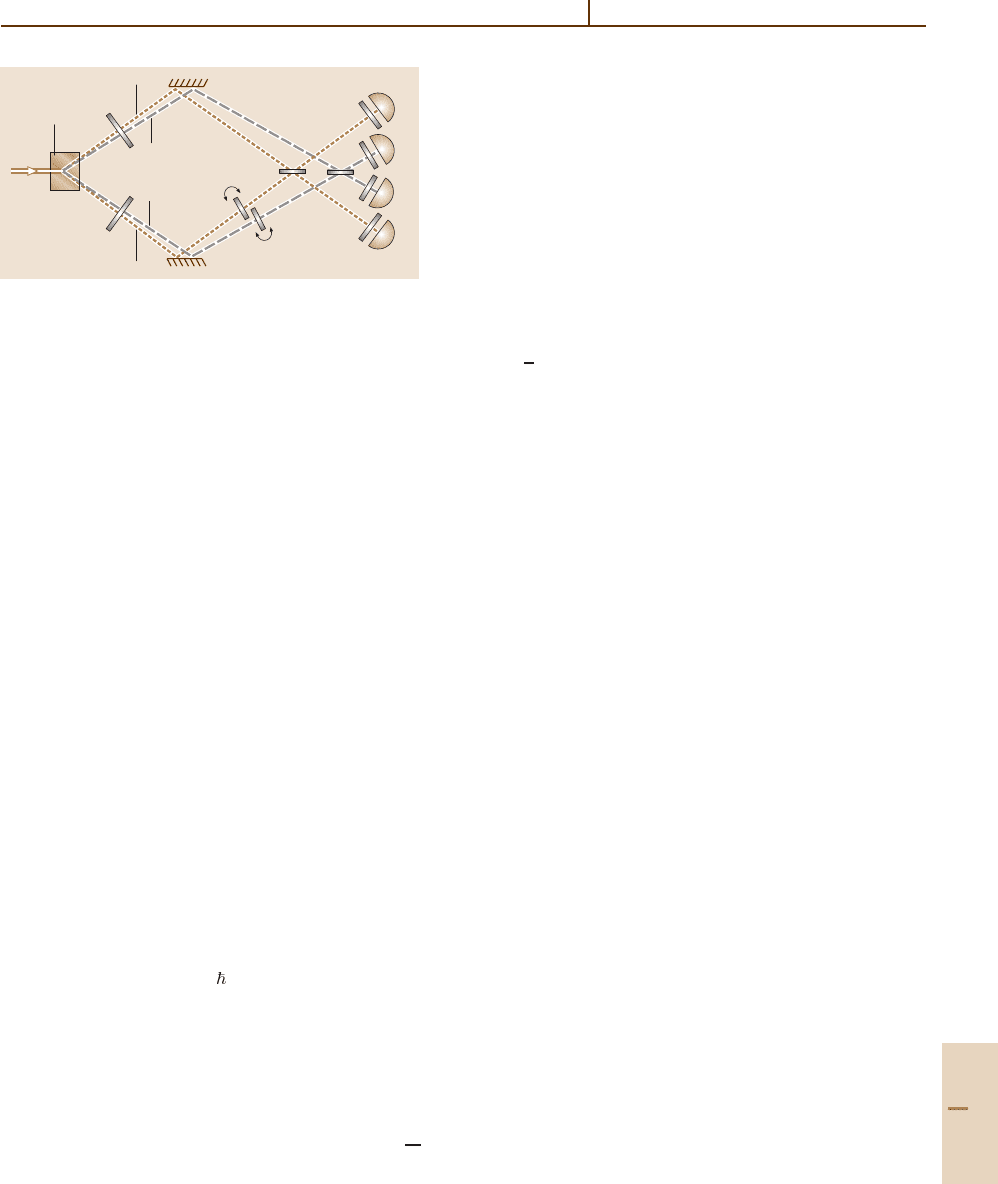
Quantum Optical Tests of the Foundations of Physics 80.6 The EPR Paradox and Bell’s Inequalities 1197

KD*P



Fig. 80.8 Outline of Rarity and Tapster apparatus used

to demonstrate a violation of a Bell’s inequality based on

momentum entanglement [80.183]

1s and 1i correspond to one pair of conjugate photons;

beams 2s and 2i correspond to a different pair. Photons

in beams 1s and 2s have the same wavelength, as do

photons in beams 1i and 2i. With proper alignment, af-

ter the beam splitters there is no way to tell whether

a pair of photons came from the 1s–1i or the 2s–2i

paths. Consequently, the coincidence rates display inter-

ference, although the singles rates at the four detectors

indicated in Fig. 80.8 remain constant. This interference

depends on the difference of phase shifts induced by

rotatable glass plates P

and P

in paths 1i and 2s, re-

spectively, and is formally equivalent to the polarization

case considered above, in which it is the difference of

polarization-analyzer angles that is relevant. By measur-

ing the coincidence rates for two values for each of the

phase shifters – a total of four combinations – the ex-

perimenters were able to violate an appropriate BI.One

interpretation is that the emission directions of a given

pair of photons are not elements of reality.

Momentum conservation in the down-conversion

process (80.4) also leads to entanglement directly in the

spatial modes in the correlated photons. For example,

Zeilinger et al. [80.184, 185]andWhite et al. [80.186]

have demonstrated entanglement between the orbital an-

gular momentum of the photons, of the form (|+1,

−1+|0, 0+|−1, +1, where 0 and ±1 respectively

denote modes with no orbital angular momentum (gaus-

sian spatial proﬁles) and ±

(Laguerre–Gauss-Vortex

modes). Note that this enables one to investigate cor-

relations for degrees of freedom that reside in larger

Hilbert spaces than do the 2-level systems (e.g., polariza-

tion) discussed above. The nonlocal spatial correlations

of the down-conversion photons have also given rise to

many interesting experiments in the area of quantum

imaging [80.187–190], where one is able to obtain spa-

tial resolution beyond that predicted by the usual

√

shot-noise limitations.

Several groups [80.191, 192] have violated a BI

based on energy–time entanglement of the pho-

tons [80.193]. In the method due to Franson, one

member of each down-converted pair is directed into an

unbalanced Mach–Zehnder-like interferometer, allow-

ing both a short and long path to the ﬁnal beam splitter;

the other photon is directed into a separate but simi-

lar interferometer. There arises interference between the

indistinguishable processes (“short–short” and “long–

long”) which could lead to coincidence detection. Using

fast detectors to select out only these processes, the

reduced state (80.9)is

|ψ=



, S

−e

iφ

, L





, (80.10)

where the letters indicate the short or long path, and

the phase is the sum of the relative phases in each

interferometer. Although no fringes are seen in any of

the singles count rates, the high-visibility coincidence

fringes (Fig. 80.9) lead to a violation of an appropriate

BI. One conclusion is that it is incorrect to ascribe to

the photons a deﬁnite time of emission from the crystal,

or even a deﬁnite energy, unless these observables are

explicitly measured.

This same sort of arrangement, modiﬁed to work

with a pulsed pump, has been used to demonstrate the

longest violation of local realism, in which Gisin’s group

has observed a 16-σ BI violation (modulo the detec-

tion and timing loopholes discussed in Sect. 80.6.4) with

photons separated by 10.9 km [80.194]. In a related ex-

periment, they have used a similar system to place limits

on the “speed of collapse” of the 2-photon wave func-

tion, i. e., how fast a nonlocal “signal” would need to

propagate from one side of the experiment to the other

to account for the measured nonclassical correlations.

Depending on some assumptions about the detection

process and which inertial frame of reference is consid-

ered, the nonlocal-inﬂuence speed was constrained to be

at least 10

c to 10

c [80.195]. In one interesting vari-

ant, the researchers arranged to have moving detectors,

such that in the local reference frame of each detector, it

was the other detector which initiated the collapse. (Due

to the experimental difﬁculty of accelerating actual de-

tectors to high velocities, a rapidly rotating absorbing

disk was placed close to one output port of a polarizing

beamsplitter; following ideas discussed in Sect. 80.5.3,

the non-absorbance of the photon by the absorber was

deemed sufﬁcient to cause a reduction of the wave func-

tion.) As expected, the measured correlations were in no

way reduced, but this experiment did rule out one alter-

native theory of nonlocal collapse [80.196,197]. Finally,

Part F 80.6

1198 Part F Quantum Optics

700

600

500

400

300

200

100

Coincidence counts N

(per 24 s)

Interferometer 1 phase shift,



= 0° = 90°

Visib. = 92.8  0.9 % Visib. = 90.3  0.7%

Fig. 80.9 High-visibility coincidence fringes in a Franson

dual-interferometer experiment [80.192] for two values of

the phase in interferometer 2 as the phase in interferometer 1

is slowly varied. The curves are sinusoidal ﬁts

by using more than two possible creation times, e.g.,

with a mode-locked pulsed laser, Gisin’s group demon-

strated entanglement for a two-photon state in a Hilbert

space of at least dimension 11 [80.198].

EPR-like correlations have also been observed di-

rectly between two correlated ﬁeld modes via homodyne

tomography [80.199], though the joint Wigner function

is positive-deﬁnite here. In contrast, a homodyne meas-

urement on the state of a single photon split between two

paths (Sect. 80.4.4) took advantage of the nonclassical

nature of the initial state to violate a Bell inequality

[80.46]. Like all existing Bell-inequality experiments,

this work suffered from several loopholes (Sect. 80.6.4),

but a new proposal suggests that the high efﬁciency of

homodyne detection may provide a unique opportunity

for a loophole-free test of Bell’s inequalities [80.200].

80.6.4 Bell Inequality Loopholes

In fact, to date no single experiment has unambigu-

ously violated a Bell inequality, due to the existence

of two experimental challenges, the detection and local-

ity “loopholes”. All of the experiments discussed thus

far have required supplementary assumptions, e.g., the

“fair-sampling” assumption that the fraction of pairs de-

tected is representative of the entire ensemble emitted by

the source. [In fact, for the entangled photons emitted in

the atomic cascade experiments, this assumption is man-

ifestly false, because the strong polarization correlations

only exist for those photons emitted nearly in opposite

directions. If one were to collect all of the emitted pho-

ton pairs, they would not lead to a violation (see [80.201]

for a fuller discussion).] To close the locality (or “tim-

ing”) loophole requires that the analyzer settings be

switched rapidly and randomly, in order to guaran-

tee that no (sub)luminal information transfer could

account for the observed correlations. The necessary

conditions have been met only in the down-conversion

experiment by Zeilinger et al., which separated the

photons by 400 m and used ultrafast random number

generation and electronic polarization-analysis choice

to ensure space-like separated observers [80.178]. How-

ever, in that experiment the detection efﬁciency was less

than 5%.

In order to understand the detection loophole,

consider the Clauser–Horne (CH) form of the Bell in-

equality [80.164], which relates the directly observable

singles rates S

and S

and the coincidence rate C

rather than “inferred” probabilities, by

(a, b) +C

(a, b



) +C



, b) −C



, b



)

≤ S

(a) +S

(b), (80.11)

where a and a



(b and b



) are any pair of analyzer (e.g.,

polarizer) settings at detector 1 (2). For certain choices

of a, a



, b,andb



, quantum mechanics predicts the left

hand side of the CH inequality can exceed the right

hand side. However, in practice this is very difﬁcult to

observe, since the coincidence rates fall as η

(η is the

detection efﬁciency), compared to the singles rates on

the right hand side, which fall only as η. In order to close

the detection loophole, one requires η ≥ 83% [80.201]

(for maximally entangled photons. (Eberhard has shown

that the required detection efﬁciency may be reduced to

67% by using nonmaximally entangled quantum sys-

tems [80.202, 203]. The idea is that one can choose the

analysis settings a and b to reduce the value of the RHS

of the CH inequality.) In essence, one requires high de-

tection efﬁciencies to ensure that the contributions from

undetected events are not sufﬁcient to cause the total

ensemble to satisfy the Bell inequality even while the

detected events violate it.

To date, only the entangled-ion experiment of

Wineland et al. [80.204] has had sufﬁciently high

efﬁciencies to close the detection loophole. In this ex-

periment the entangled variables were the hyperﬁne

energy levels of

ions. By employing a cy-

cling transition that leads to the emission of many

photons if the atom is in one of the states, a de-

tection efﬁciency in excess of 98% was achieved,

allowing an 8-σ Bell inequality violation. However,

because the ions were separated by only 3 µmin

the same linear Paul trap, and in fact were measured

Part F 80.6

Quantum Optical Tests of the Foundations of Physics 80.6 The EPR Paradox and Bell’s Inequalities 1199

using the same laser pulse, there was no possibil-

ity of closing the locality loophole. More recently,

Monroe et al. have demonstrated the entanglement

of a trapped ion and a photon [80.205], and have

used this to violate a Bell inequality [80.206]. Sim-

ilar experiments have also enabled the production of

up to four entangled ions [80.207]. Though neither

of the experimental loopholes was closed in these

experiments, they are noteworthy as the ﬁrst con-

trolled demonstrations of entanglement in massive

particles. Efforts are now underway to attempt a di-

rect violation of (80.11) with no auxiliary assumptions

using down-conversion photons and high-efﬁciency

(> 85%) single-photon detectors [80.208, 209], in ad-

dition to atomic schemes [80.210] and homodyne

schemes [80.200] (Sect. 80.6.3), which enjoy even

higher intrinsic efﬁciency.

80.6.5 Nonlocality Without Inequalities

In the above experiments for testing nonlocality, the

disagreement between quantum predictions and Bell’s

constraints on local realistic theories are only statistical.

Greenberger, Horne,andZeilinger (GHZ) pointed out

that in some systems involving three or more entangled

particles, a contradiction could arise even at the level of

perfect correlations [80.211, 212]. A schematic of one

version of the GHZ Gedankenexperiment is shown in

Fig. 80.10. The source at the center is posited to emit

aa

c

b

α

γ

β

Fig. 80.10 A three-particle Gedankenexperiment to demon-

strate the inconsistency of quantum mechanics and any local

realistic theory. All beam splitters are 50–50 [80.111]

trios of correlated particles. Just as the Rarity–Tapster

experiment selected two pairs of photons (Fig. 80.8),

the GHZ source selects two trios of photons; these are

denoted by abc and a



. Hence, the state coming from

the source may be written

|ψ=



|abc+|a







√

2 . (80.12)

After passing through a variable phase shifter (e.g., φ

each primed beam is recombined with the correspond-

ing unprimed beam at a 50–50 beam splitter. Detectors

(denoted by Greek letters) at the output ports signal

the occurrence of triple coincidences. The following

simpliﬁed argument conveys the spirit of the GHZ result.

Given the state (80.12), one can calculate from

standard QM the probability of a triple coincidence as

a function of the three phase shifts:

P(φ

,φ

) =

[

1 ±sin(φ

+φ

)

]

(80.13)

where the plus sign applies for coincidences between

all unprimed detectors, and the minus sign for coin-

cidences between all primed detectors. For the case in

which all phases are 0, it will occasionally happen (1/8th

of the time) that there will be a triple coincidence of all

primed detectors. Using a “contrafactual” approach, we

ask what would have happened if φ

had been π/2in-

stead. By the locality assumption, this would not change

the state from the source, nor the fact that detectors



and γ



went off. But from (80.13) the probability

of a triple coincidence for primed detectors is zero in

this case; therefore, we can conclude that detector α

would have “clicked” if φ

had been π/2. Similarly, if

or φ

had been π/2, then detectors β or γ would

have clicked. Consequently, if all the phases had been

equal to π/2, we would have seen a triple coincidence

between unprimed detectors. But according to (80.13)

this is impossible: the probability of triple coincidences

between unprimed detectors when all three phases are

equal to π/2 is strictly zero! Hence, if one believes the

quantum mechanical predictions for these cases of per-

fect correlations, it is not possible to have a consistent

local realistic model.

Down-conversion experiments have enabled the pro-

duction of 3- and 4-photon GHZ states, with results

in good agreement with theory (the all-or-nothing ar-

guments given above become inequalities in any real

experiment) [80.37–39].

By similar arguments, Hardy has shown the incon-

sistency of quantum mechanics and local realism in

a Gedankenexperiment with just two particles [80.213,

214]. When the arguments are suitably modiﬁed to

Part F 80.6