Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

SECTION 7.2 ROTATIONS OF SUBSPACES 169

a x a

−1

−a

x a

−1

a)/a

Figure 7.1: Line and plane reﬂection of a vector x in a vector a, used as line direction or as

normal vector for the plane A.

This hyperplane reﬂection is actually what we mean by a reﬂection—in 3-D, it reﬂects in

a plane, which is like looking into a mirror. It extends to blades by outermorphism as the

linear transformation a:



→



deﬁned by

reﬂection of X in dual hyperplane a: X → a[X] ≡ a



−1

, (7.2)

where



X = (−1)

grade(X)

X is the grade involution.

To be a reﬂection, its determinant should be −1 in a space of any dimensionality. With

the pseudoscalar of n-dimensional space denoted as I

, we can check this easily using

deﬁnition (4.7) of a determinant in geometric algebra:

det(a) = (a



−1

) I

−1

= a (



−1

) I

−1

= a (−a

−1

) I

−1

= −1.

Here we used the fact that a is contained in the space I

, and therefore a ∧ I

= 0,so

that aI

= −



a. So the determinant is indeed −1. If you would repeat the determinant

computation for the line reﬂection, you would ﬁnd (−1)

n+1

for the determinant in

n-dimensional space. This shows that in 3-D, a line reﬂection is actually not a reﬂection

but a rotation (see structural exercise 3). By contrast, hyperplane reﬂections are indeed

proper reﬂections in any dimension.

7.2 ROTATIONS OF SUBSPACES

Having reﬂections as a sandwiching product leads naturally to the representation of rota-

tions. For by a well-known theorem, any rotation can be represented as an even number

of reﬂections. In geometric algebr a, this statement can be converted immediately into a

computational form.

170 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

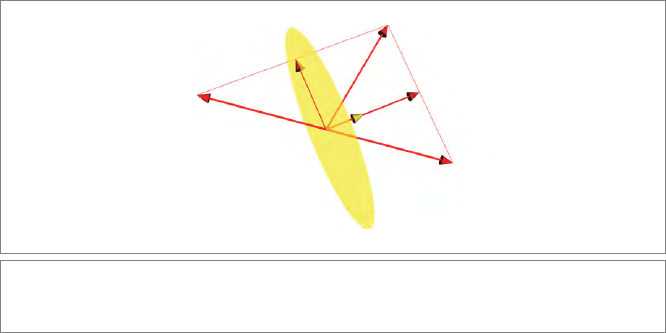
7.2.1 3-D ROTORS AS DOUBLE REFLECTORS

Two reﬂections make a rotation, even in R

(see Figure 7.2). Since an even number of

reﬂections absorbs any sign, we may make these reﬂections either both line reﬂections

axa

−1

or both (dual) hyperplane reﬂections −axa

−1

, whichever feels most natural or is

easiest to visualize. The ﬁgure uses line reﬂections.

As the ﬁgure shows, ﬁrst reﬂecting in a, then in b, gives a rotation over an axis perpen-

dicular to the a ∧b-plane, over an angle that is twice the angle from a to b (and this angle

and plane also give the sense of rotation, clockwise or anticlockwise in the plane). In this

construction, only the plane and relative angle of the vectors a and b matter.

GAViewer

or the programming example in Section 7.10.2 each provide an interactive version. We

strongly recommend playing with either if you need to tune your intuition.

It is simple to convert this geometrical idea into algebra. The operation

x → b (axa

−1

) b

−1

= ba

−1

xab

−1

= (b/a) x (b/a)

−1

is the double reﬂection, and therefore produces the rotation in the a ∧b plane (we moved

some scalar squared norms around to get a pleasant expression). We observe that this

rotation is generated by an element R = b/a = ba

−1

, as applied to a vector by the recipe

rotation of x: x → R x R

−1

Figure 7.2: A rotation in a plane is identical to two reﬂections in vectors in that plane,

separated by half the rotation angle.

SECTION 7.2 ROTATIONS OF SUBSPACES 171

Note that this element R is not necessarily a blade, since it is a geometric product. That

is why we do not denote it by a bold symbol. It deﬁnes a linear transformation that we

denote by R[].

Since rotation is a linear transformation, it can be extended as an outermorphism. You

can easily show by mimicking the proof of (7.1) that a blade X rotates to R[X] deﬁned by

rotation of X: X → R[X] ≡ R X R

−1

(7.3)

There are no extra signs in this transformation formula, unlike the reﬂection formula of

(7.2); the double reﬂection has canceled them all. As a consequence, the determinant of

a rotation is +1 in a space of any dimension:

det(R) = (R I

−1

)/I

= RR

−1

= 1.

Geometrically, this means that there is no orientation change of the pseudoscalar.

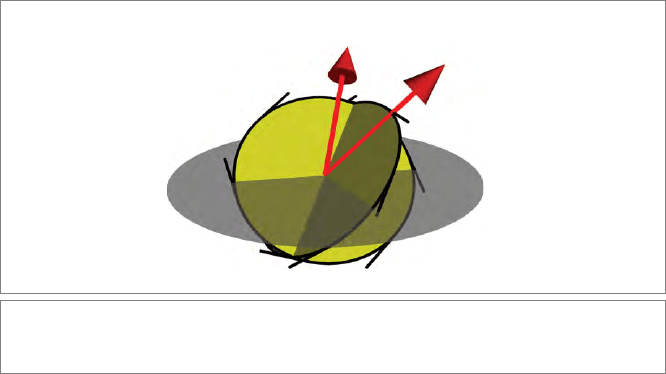
Equation (7.3) can even be extended to arbitrary multivectors, for the rotation is linear.

That means that we are now capable of rotating any multivector, not just a vector, with

the same formula. In 3-D, this is already helpful: we can rotate a plane (represented as a

2-blade) directly without having to dualize it ﬁrst to a normal vector (see Figure 7.3). On

the other hand, if it had been given dually, we could rotate it in that form as well. These

capabilities extend to higher-dimensional spaces and in Part II will permit us to rotate

Euclidean circles, spheres, and other elements, all using the same operation.

It is common practice to take out the scaling factor in R = b/a, reducing it to a unit

element called a rotor. That obviously makes no difference to the application to a blade,

R x / R

R A / R

Figure 7.3: The same operation RX/R rotates a vector, a 2-blade, or any element of the

algebra.

172 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

since any scaling factor in R is canceled by the reciprocal factor in R

−1

. To compute the

normalization of a rotor, we need to compute the scalar product of a mixed-grade multi-

vector, which we have not done before. Using (6.22) and (6.23), it is straightforward:

R

= R ∗



R = ba

−1

b

= b

−1

)



= b

Therefore R = ±b/a, and dividing it out produces a properly normalized rotor.

To construct a rotor to represent the rotation from a to b, we can either do what we just

did (start with general a and b and taking out the norm ratio), or just deﬁne it as the ratio

of two unit vectors b and a from the start. When we do the latter, R = ba

−1

= ba, and

−1

= ab=



R . It follows that the inverse of a rotor is its reverse:



R = 1,

so that the rotation of X can be performed as R[X] = R X



R . Performing the normal-

ization once is often better in practice than having to compute its inverse with each

application, so we will use these normalized rotors constructed from unit vectors as the

representation of rotations in this chapter.

7.2.2 ROTORS PERFORM ROTATIONS

It is natural to relate the rotor b/a to the geometrical relationships of the two vectors:

their common plane a ∧ b and their relative angle. We can use those geometric elements

to encode it algebraically, by developing the geometric product of the unit vectors in terms

of their inner and outer product, and those in terms of angle and plane. Since b and a were

assumed to be unit vectors, we have b/a = ba, and compute

R = ba= b · a + b ∧ a = cos(␾/2) − I sin(␾/2),

(7.4)

where ␾/2 is the angle from a to b, and I is the unit 2-blade for the (a ∧ b)-plane. This

rotor involving the angle ␾/2 actually rotates over ␾ (as Figure 7.2 suggests, and as we will

show below).

The action of a rotor may appear a bit magical at ﬁrst. It is good to see in detail how the

sandwiching works to produce a rotation of a vector x in a Euclidean space. To do so, we

introduce notations for the various components of x relative to the rotation plane. What

we would hope when we apply the rotor to x is that

•

The component of x perpendicular to the rotation plane (i.e., the rejection x

↑

deﬁned by x

↑

≡ (x ∧ I)/I ) remains unchanged;

•

The component of x w ithin the plane (i.e., the projection x



≡ (xI)/I ) gets short-

ened by cos ␾;

•

A component of x perpendicular to the projection in the plane (i.e., x

⊥

≡ x





I = x



I) gets added, with a scaling factor sin ␾.

SECTION 7.2 ROTATIONS OF SUBSPACES 173

It seems a lot to ask of the simple formula R x



R , but we can derive that this is indeed

precisely what it does. The structure of the derivation is simpliﬁed when we denote c ≡

cos(␾/2), s ≡ sin(␾/2), and note beforehand that the rejection and projection satisfy the

commutation relations x

↑

I = Ix

↑

and x



I = −Ix



(these relations actually deﬁne them

fully, by the relationships of Section 6.3.1). Also, we have seen in (6.4) that in a Euclidean

space I

= −1, which is essential to make the whole thing work. Then

R x



R = R (x

↑

+ x



)



= (c − sI)(x

↑

+ x



)(c + sI)

= c

↑

− s

(Ix

↑

I) + cs(x

↑

I − Ix

↑

) + cs(x



I − Ix



) + c



− s

(Ix



= (c

+ s

) x

↑

+ (c

− s

) x



+ 2cs x



= x

↑

+ cos ␾ x



+ sin ␾ x

⊥

which is the desired result. Note especially how the vector x

⊥

, which was not or iginally

present, is gener ated automatically. It is very satisfying that the whole process is driven

by the algebraic commutation rules that encode the various geometrical perp endicular-

ity and containment relationships. This shows that we truly have an algebra capable of

mimicking geometry.

The unit vectors in the directions x

↑

, x



, and x

⊥

form an orthonormal basis for the rel-

evant subspace of the vector space involved in this rotation. The rotor application has

constructed this frame automatically from the vector x that needs to be rotated. This is in

contrast to rotation matrices, which use a ﬁxed frame for the total space that is unrelated

to the elements to be processed. Such a ﬁxed frame then necessitates a lot of coordinate

coefﬁcients to represent an arbit rary rotation. Even when the frame has been well chosen

(so that for instance e

∧ e

is the rotation plane), the sine and cosine of the angle occur

twice in the rotation matrix:

[[

R]] =

⎡

⎢

⎣

⎡

⎢

⎣

cos ␾ −sin ␾ 0 ··· 0

sin ␾ cos ␾ 0 ··· 0

001··· 0

000··· 1

⎤

⎥

⎦

⎤

⎥

⎦

When multiplying rotations, this double occurrence causes needless double work that

rotors avoid (like quaternions; we show the relationship in Section 7.3.5). So although it

would seem like a waste to construct a new frame for each vector, the rotation representa-

tion we have shown can actually be more efﬁcient than a rotation matrix implementation.

After all, we never actually construct the frame; we merely perform R x



R .

There is a classical way of generating a 3-D rotation matrix that is also based on the

construction x

↑

+ cos ␾ x



+ sin ␾ x

⊥

.ItisRodrigues’ formula, which uses a unit vector a

174 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

in the direction of the rotation axis to construct x

↑

= a (a·x), x



= x−a (a·x), x

⊥

= a×x,

resulting in the rotation matrix

Rodrigues’ formula: [[ R]] = [[ a]] [[ a]]

+ cos ␾ ([[1]] − [[ a]] [[ a]]

) + sin ␾ [[ a

]] ,

where [[ a

]] is the matrix corresponding to the cross product operation. This is a

coordinate-free speciﬁcation of an operator based on geometric principles. The geometric

principle may be the same as before, but note that this formula is an explicit construction

rather than an automatic consequence. Unfortunately it only works in 3-D (as the use of

the cross product betrays). Moreover, it constructs a matrix that only applies to vectors

rather than a universal rotation operation.

We emphasize that for a rotation, the bivector angle I␾ contains all information: both the

angle and the plane in which it should be measured. From this bivector angle, one can

immediately construct the rotor performing the corresponding rotation. We will see a

straightforward method for that in Section 7.4, and may write R

I␾

to foreshadow this.

7.2.3 A SENSE OF ROTATION

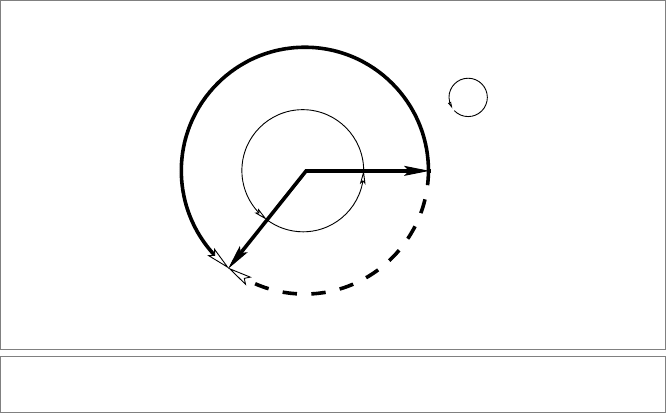
Using the transformation formula x → R x



R ,weseethatarotorR and “minus that

rotor” (−R) give the same resulting rotation. This does not necessarily mean that the

representation of rotations by rotors is two-valued: these rotors can be distinguished when

doing relative rotations of connected objects. Such relative rotations can be achieved in

two ways: by going clockwise or counterclockwise. You may think that you cannot tell

from the result which it was, but it is useful to discriminate them in some applications (it

can prevent you from curling up the wires on your robot). Let us call this property the

sense of a rotation. It comes for free with the rotor representation.

We derive the rotation angle for the negative rotor −R

I␾

by rewriting it into standard

form:

−R

I␾

= −cos( ␾/2) + I sin(␾/2)

= cos



(2π + ␾)/2



− I sin



(2π + ␾)/2



= R

I(2π+␾)

(7.5)

It is now obvious that R

I␾

and −R

I␾

lead to the same result on a vector since a rotation

over 2π + ␾ is the same as a rotation over ␾, see Figure 7.4. Yet the following real-life

experiment called the plate trick shows that this is actually not true for connected objects.

Hold out your hand in front of your shoulder, a hand-length away, palm upwards

and carrying a plate. Now make a motion with your arm that rotates the plate hor-

izontally in its plane over 2π. After completion, you will have your elbow sticking

up awkwardly in the air. Continue the plate rotation over another 2π (you may

have to wriggle your body a little to keep the plate turning in its plane). Perhaps

SECTION 7.2 ROTATIONS OF SUBSPACES 175

−R

Iφ

= R

−I(2π−φ)

= R

I(2π+φ)

R x R

I(2π−φ)

Iφ

Figure 7.4: Sense of rotation.

surprisingly, both you and the plate are now back in their original position: a 4π

rotation equals the identity on coupled bodies. This is a more subtle result than the

usual statement: a 2π rotation equals the identity for isolated elements (like a plate

by itself).

The shortest way to achieve an angle of 2π + ␾ for the plate (with the same position of

the elbow) is to turn the other way over 4π −(2π + ␾) = 2π −␾. Therefore it makes sense

to say that −R

I␾

is a rotation over that effective angle, but in the opposite direction. That

geometrical insight is conﬁrmed by evaluating the negated rotor by a different algebraic

route:

−R

I␾

= −cos(␾/2) + I sin(␾/2)

= cos((2π − ␾)/2) + I sin((2π − ␾)/2)

= R

−I(2π−␾)

This is indeed the rotation over the complementary angle 2π − ␾, in the plane −I with

opposite orientation, see Figure 7.4. Therefore we can uniquely assign the rotor’s angles

in the range [0, 4π) to actual rotations of different magnitudes and senses, as in Figure 7.5.

Comparing this ﬁgure with the sign changes of the sine and cosine of half the rotation

angle gives a clear test for which the rotation exactly is encoded by a given rotor R.

•

The cosine cos(␾/2) = R

changes sign as |␾/2| exceeds π/2, so exactly when the

absolute value of the effective rotation angle ␾ exceeds π. A positive value of the

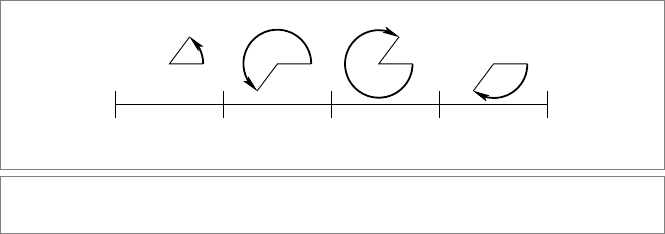
176 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

2π 3π 4π

Figure 7.5: The unique rotor-based rotations in the range ␾ = [0,4π).

scalar part of the rotor tells you that this is a rotation over the smallest angle

(whether clockwise or counterclockwise).

•

The sign of sin(␾/2) = R

I gives the sense of rotation: positive indicates a rotation

following the orientation of I, negative follows the orientation of −I.

The occurrence of I in the expression for the sense of rotation is necessary: since I deﬁnes

what orientation we mean by (counter)clockwise, the sense of rotation should also change

when we change the sign of I.

Mathematically, it is often said that the rotors constitute a double covering of the rota-

tion group—one physical rotation is being represented in two distinct ways (R and −R).

We now see how this sign actually conveys geometrically signiﬁcant information about

the rotation process rather than the rotation result. Hestenes [29] calls the rotors oriented

rotations, which is a good term to have. It is the half-angle representation that enables us

to distinguish the var ious orientations.

7.3 COMPOSITION OF ROTATIONS

The composition of rotations follows automatically from their representation as a geo-

metric product:

The rotor of successive rotations, ﬁrst R

then R

, is their geometric product R

This is easily shown by associativity of the geometric product, since R



)



) x (R

)



. That the result is indeed a rotor follows from (R

)(R

)



= 1.

We expand this composition in detail in this section to sharpen our intuition, both alge-

braically and geometrically, and to relate it to other rotation representations such as

complex numbers and quaternions.

SECTION 7.3 COMPOSITION OF ROTATIONS 177

7.3.1 MULTIPLE ROTATIONS IN 2-D

If we rotate in a single plane with pseudoscalar I, we are effectively dealing with rotations

in a 2-D Euclidean subspace

2,0

. Performing the 2-D rotation R

I␾

after R

I␾

results in

the total rotation R

I(␾

+␾

)

, as you would expect. This also shows that planar rotations

commute.

The algebraic demonst ration is straightforward:

I␾



cos(␾

/2) − I sin(␾

/2)



cos(␾

/2) − I sin(␾

/2)





cos(␾

/2) cos(␾

/2) − sin(␾

/2) sin(␾

/2)



−I



cos(␾

/2) sin(␾

/2) + sin(␾

/2) cos(␾

/2)



= cos((␾

+ ␾

)/2) − I sin((␾

+ ␾

)/2)

= R

I(␾

+␾

)

Algebraically, this looks like the standard computation using a product of complex num-

bers, since I

= −1. We prefer to view it as a calculation in the real geometric algebra of

coplanar elements.

In 2-D, rotations do not actually require the rotor sandwiching product R x



R to be

applied. Since any vector x in the I-plane satisﬁes the anticommutation relationship

xI= −Ix, we can bring a rotor to the other side:

I␾

x R

−I␾



cos(␾/2) − I sin(␾/2)





cos(␾/2) + I sin(␾/2)



= x



cos(␾/2) + I sin(␾/2)



cos(␾/2) + I sin(␾/2)



= x



cos ␾ + I sin ␾



(7.6)



cos ␾ − I sin ␾



The two ﬁnal lines show alternative forms for the one-sided planar rotation. We have

met the ﬁnal form, using left multiplication, when we did the motivating problem in

Section 6.1.6.

In summary, in a plane (and in a plane only!) the half-angle rotors in the sandwiching

product can be converted to whole-angle, one-sided products using either left or right

multiplication.

7.3.2 REAL 2-D ROTORS SUBSUME COMPLEX NUMBERS

We have just shown how the rotation of a vector x in a plane I containing it can be sim-

pliﬁed from the two-sided sandwiching form to a postmultiplication:

x → x (cos ␾ + I sin ␾ ). (7.7)

Because I

= −1, this is reminiscent of complex numbers, a well-known tool to perform

rotations in the complex plane. Yet our approach must be subtly different, for the vector

178 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

x anticommutes with the 2-blade I (i.e., xI = −Ix), whereas if x and I had been complex

numbers they should have commuted with each other. Also, we are in a real plane, not in

a complex plane at all. What is going on here? How can such different algebras lead to the

same (or at least isomorphic) results?

The answer lies in the special role of the real axis in the complex plane. The selection of

such a special reference direction destroys the geometrical symmetries of the plane and

changes the algebra of the symbols. Let e be the unit vector in the direction of the real

axis, then a complex number X corresponding to the vector x in the plane denotes how

to rotate and scale e to get to x. In terms of geometric algebra, this is the ratio X = x/e

(see Section 6.1.6). So

a complex number is a geometr ic ratio of a vector to a ﬁxed vector.

To be speciﬁc, the complex number corresponding to a vector a = a

+ a

in the

I ≡ e

∧ e

-plane relative to the ‘real axis’ e

A = a/e

= a

− a

I. (7.8)

The original vector addition can of course be lifted to these complex numbers by linearity

of the geometric product:

A + B = (a/e

+ b/e

) = (a + b)/e

= (a

+ b

) − (a

+ b

) I.

Two such complex numbers multiply according to the geometric product:

AB= (a

− a

I)(b

− b

I) = (a

− a

) − (a

+ a

) I.

This product is obviously commutative. With sum and product thus deﬁned, our complex

numbers are clearly isomorphic to the usual complex numbers and their multiplication,

if you set i ≡−I.

Yet we will not use complex numbers to do geometry in the plane, for they lose the dis-

tinction between vectors and operators; the vectors have effectively become represented as

rotation/scaling operators. The capability to describe such operators compactly was part

of the attr action of complex numbers when they were ﬁrst introduced. But we really want

both vectors and operators in our geometry, so we want all elements that can be made in

the basis:

{1, e

, e

∧ e

= I}.

That is precisely what the geometric algebra of the plane provides, in an integrated manner

that also contains the algebraic and geometrical relationships between vectors and oper-

ators. Complex numbers only use the basis {1,I}. They are only half of what is required

to do all of Euclidean planar geometry.

To show the power of this way of looking at complex numbers, programming

exercise 7.10.5 computes the fractal Julia sets using only real vectors. That formulation

makes their extension to n-dimensional space straightforward.