Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry
Подождите немного. Документ загружается.

138 INTERSECTION AND UNION OF SUBSPACES CHAPTER 5
4. Compute the meet and join of two parallel vectors u and v.Themeet should now
be symmetric. (Hint: Use one of them as the
join.)
5. As an exercise in symbolic manipulation of the products so far, let us consider the
meet of a ∧B and a∧C,wherea is a vector and the blades B and C have no common
factor. The answer should obviously be proportional to a, but what precisely is the
proportionality factor? (Hint: If you get stuck, the next exercise derives the answer
as (a ∧ B ∧ C)
∗
.)
6. Verify the steps in the following computation of the answer to the previous exercise.
They are rather ingenious; note the third step especially, and the conversion to a
scalar product (check the grades involved!). The
join for dualization should be a
blade proportional to a ∧ B ∧ C (if it is zero our suppositions are wrong, and vice
versa). Here goes:
(a ∧ B) ∩ (a ∧ C) =
(a ∧ C)
∗
∧ (a ∧ B)
∗
−∗
=
(aC
∗
) ∧ (aB
∗
)
−∗
=
a
C
∗
∧ (aB
∗
)
−∗
=
a
C
∗
∧ (a ∧ B)
∗
−∗
= a ∧
C
∗
(a ∧ B)
= a ∧
C
∗
∗ (a ∧ B)
= a ∧
(a ∧ B) ∗ C
∗
= a ∧
(a ∧ B)C
∗
= a ∧ (a ∧ B ∧ C)
∗
.
7. Use the previous derivation to derive the general factorization of the
meet:
(A ∧ B) ∩ (A ∧ C) = A (A ∧ B ∧ C)
∗
, (5.11)
where A, B, and C have no common factors.
5.11 PROGRAMMING EXAMPLES AND EXERCISES
5.11.1 THE MEET AND JOIN
This example allows you to interactively select and manipulate two multivectors. The
multivectors can be vector-valued or 2-blade-valued. Either the
meet or the join of the
multivectors are dr awn:
// M1 and M2 are the two multivectors
mv X;
if (g_draw == DRAW_MEET) X = meet(M1, M2);
else X = join(M1, M2);
// ... (set color, scale)
draw(X);
Note that we use multivectors (class mv) here because neither the input nor the output
has a fixed multivector type. As demonstrated in the next example, working with the
mv
SECTION 5.11 PROGRAMMING EXAMPLES AND EXERCISES 139
class in general and the meet() and join() functions in particular is much slower than
the specialized classes and the ordinary products.
To make it easier to produce degenerate cases—such as two parallel vectors—we round
the coordinates of multivectors
M1 and M2 to multiples of 0.2. This causes them to move
in a stepwise fashion.
5.11.2 EFFICIENCY
In Gaigen 2, the implementation of the meet and join is very slow compared to the other
products. This example performs a benchmark to demonstrate this. It creates 1,000,000
pairs of random vectors and bivectors. It then times how long it takes to compute the
outer product of these pairs, and how long it takes to compute the
join of these pairs. In
our benchmark the
join is about 100 times slower than outer product. There are several
reasons for this:
•
To compute the meet and join, a specialized (factorization) algorithm is used,
whereas computing the outer product is as simple as multiplying and summing
coordinates in the right way. See Section 21.7 for a description of the
meet and
join algorithm used in this example.
•
The algorithm uses the mv class instead of the specialized types such as vector and
bivector.Themv class uses coordinate compression, which is slow.
•
The ordinary subspace products are just very efficient in Gaigen 2.
It may be possible to optimize the
meet and join toalevelwheretheyareabout10
times slower than the regular products. But in general, you should try to avoid the
meet
and join in your programs if you care about efficiency. If you know the relative posi-
tion of elements involved, just use the formula B
∗
A in the appropriate subspace instead
of A ∩ B.
5.11.3 FLOATING POINT ISSUES
As stated above, the meet and join are computed by a factorization algorithm. Before the
factorization starts, the algorithm computes what the grade of the output should be. This
involves comparing a condition number (similar to that of a matrix) to a small threshold
value. Hence, the algorithm will flip-flop between grades in degenerate cases (e.g., near-
parallel vectors).
This example (see Figure 5.4) searches for the point where the join of two (near-)parallel
vectors changes from a vector to a 2-blade. It starts with a very small probe epsilon of
10
−10
, and tests if e
1
∪ ( e
1
+ 10
−10
e
2
) is a 2-blade. If not, it grows the probe epsilon, and
loops. In the example, the flip-flop occurs when b = e
1
+ 1.007748 −×10
−7
e
2
,whichis
to be expected, because the
meet-join algorithm uses an epsilon of 10
−7
.

140 INTERSECTION AND UNION OF SUBSPACES CHAPTER 5
// get two vectors, initialize ’a’ to ’e1’
e3ga::vector a, b;
a = e1;
float probeEpsilon = 1e-10f;
while (true){// the loop will be broken when the join is a bivector;
// add a tiny bit of ’e2’ to b:
b = e1 + probeEpsilon * e2;
// compute the join
mv X = join(a, b);
// get analysis of ’X’
mvAnalysis AX(X);
// check if blade, and if a blade, then is it a 2-blade or a vector?
if (!AX.isBlade()) {
// this should never happen
printf("Error: the join of a and b is not a blade!\n");
return -1;
}
else {
// compute string "join(..., ...)"
std::string str = "join(" + a.toString_e() + ", " + b.toString_e() + ")";
if (AX.bladeSubclass() == mvAnalysis::BIVECTOR) {
printf("%s is a 2-blade\n", str.c_str());
return 0; // terminate
}
else printf("%s is a vector\n", str.c_str());
}
// Grow ’probeEpsilon’ a little such that it won’t take forever to reach
// the point where join(a, b) is a 2-blade:
probeEpsilon *= 1.01f;
}
Figure 5.4: Searching for the point at which the join of two (near-)parallel vectors becomes a 2-blade (Example 3).
6
THE FUNDAMENTAL
PRODUCT OF GEOMETRIC
ALGEBRA
We have seen how the outer product and the contraction characterize rather different
properties of subspaces: qualitative spanning and quantitative measurements. Together,
they have given us an enriched view of the linear algebra of subspaces. This much has
been known for some time, and is part of the branch of applied mathematics that is called
Grassmann-Cayley algebra.
In this chapter we will start afresh and introduce the basics of Clifford algebra to
develop a powerful geometric algebra. This geometric algebra will incorporate operators
on subspaces into our framework, and permit us to displace the constructions of the sub-
space algebra in a structure-preserving manner. The crucial construction is to unify the
qualitative and quantitative subspace products into a single geometric product, more fun-
damental than either. The geometric product is invertible, and it allows us to manipulate
and solve equations about geometrical quantities almost as if they were regular arith-
metical expressions. The true power of this geomet ric product will become clear in the
next chapter, when we use it to define the versor product construction for operators. This
chapter defines the geometric product, first for vectors and then for general multivectors.
Subsequently, we show how the geometric product indeed subsumes the earlier products
(which is a bit of tedious but necessary algebra), and we end with the use of its invertibility
to define general projection and rejection operations through geometric division.
141
142 THE FUNDAMENTAL PRODUCT OF GEOMETRIC ALGEBRA CHAPTER 6
6.1 THE GEOMETRIC PRODUCT FOR VECTORS
6.1.1 AN INVERTIBLE PRODUCT FOR GEOMETRY
Consider a fixed and known vector a and an unknown vector x, both in a Euclidean vector
space
R
n
. Let us assume that all we know about x is the scalar value α of its inner prod-
uct with a. Then x must satisfy x · a = α. This implies that the endpoint of x lies on
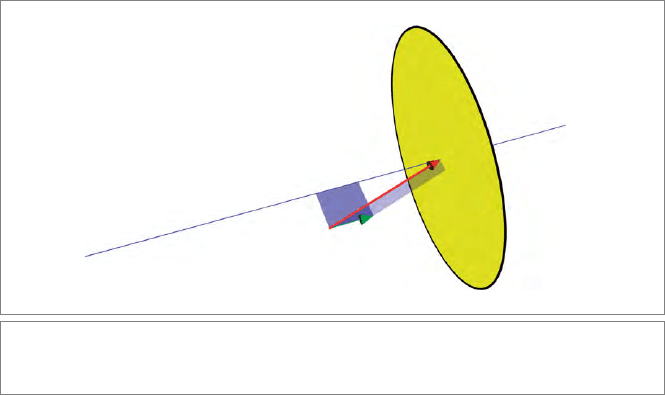
a hyperplane perpendicular to the direction of a. In Figure 6.1, this is sketched in
R
3,0
as the yellow plane. Geometrically, it is clear that we cannot retrieve x from α and a.
Algebraically, this means that there is no unique “inner division”. If there were, we could
invert the inner product and retrieve x from its product with a by means of some formula
like (x · a) /a = x.
The outer product is not much better in this respect. Suppose that we were told the value
of the outer product of a and x is to be the bivector B. That bivector must of course be
an area element of the plane shared by a and x. The equation x ∧ a = B defines a line in
space, offset from the origin. (You can see this as follows: let p be a solution of p ∧ a = B.
Then x satisfies x ∧ a = p ∧ a, so that (x − p) ∧ a = 0. We saw in Section 2.8.1 that this
implies (x − p) = λa. Therefore x = p + λa, a general point on the line through p in the
direction a.) This line has been sketched in blue in Figure 6.1. The endpoint of x must be
on this line; but knowing the line does not specify x. This is the geometrical reason why
we cannot algebraically retrieve x fr
om knowing the outer product B and a;
there is no
“outer division”, and no formula such that (x ∧ a)/a = x for all x.
We thus see that, when taken separately, the two products with a are insufficient to
retrieve x; yet they are somehow complementary. Indeed, combining the two pieces
x
?
a-plane
x ∧ a
x ∧ a - line
x
a
Figure 6.1: Combination of the noninvertible subspace products leads to the invertible geo-
metric product (see text).

SECTION 6.1 THE GEOMETRIC PRODUCT FOR VECTORS 143
of information is obviously enough to fully determine x, with its endpoint at the
intersection of the hyperplane and the line, as illustrated in Figure 6.1 for 3-D space.
Therefore a product of x and a that contains both the inner product and outer product
information should be invertible.
6.1.2 SYMMETRY AND ANTISYMMETRY
There is a clean way to construct a composite product from the inner product x·a and the
outer product x ∧ a. It is based on their symmetries. The inner product x · a is symmetric
in x and a, for it retains its value when x and a are interchanged. The outer product x ∧ a
is antisymmetric; it changes sign under exchange of x and a.
We can now make a new product between x and a such that the inner product is its sym-
metric part and the outer product its antisymmetric part. That defines it uniquely. This
product is called the geometric product (though some call it the Clifford product after its
1872 inventor William Kingdon Clifford). It is so central that we use the empty symbol ‘ ’
to denote it, writing xafor the geometric product of x and a.
The demands on its symmet ric and antisymmet ric parts give the equations
x · a =
1
2
(xa+ ax) (6.1)
and
x ∧ a =
1
2
(xa− ax). (6.2)
By adding these equations, we find that the geometric product of the vectors x and a
must be
geometric product for vectors : xa≡ x · a + x ∧ a.
(6.3)
This product of two vectors produces a multivector that consists of a scalar part and a
2-blade part. That is unusual; our previous products always produced outcomes of a single
grade. But it is precisely because the parts of different grades do not mix in an addition
that they can be retrieved separately. That makes the geometric product invertible.
6.1.3 PROPERTIES OF THE GEOMETRIC PRODUCT
Let us check the algebraic properties of this new product between vectors:
•
Commutativity. The geometric product of two general vectors is not commutative,
for the equation xa = ax would imply that x ∧ a = 0. This means that commu-
tativity only happens when x and a are parallel. On the other hand, the product is
also not anticommutative, for that would imply x · a = 0, which is also a special
relationship of x and a. As a consequence of this lack of general commutativity, we
should be very careful about the order of the factors in the product xa.
144 THE FUNDAMENTAL PRODUCT OF GEOMETRIC ALGEBRA CHAPTER 6
•
Linearity and Distributivity. The geometric product is linear and distr ibutive,
since both the inner and the outer product are, and these properties inherit under
addition.
•
Associativity. Definition 6.3 does not specify how to compute the geometric prod-
uct of more than two vector factors. We have motivated our definition because we
wanted an invertible product so that (xa)/a would be equal to x (with division
defined in terms of the geometric product). This suggests that we should define the
producttobeassociative. The desired equation then holds, since we could rewrite
it to (xa)/a = x (a/a) = x. Moreover, in an associative algebra, each invertible ele-
ment has a unique inverse, so the division would be uniquely defined. (We clarify
that point later, in Section 6.1.5.)
We give the fully general algebraic definition of the geometric product in Section 6.2.1.
But first, we would like to familiarize you with the use of having such a product for vectors,
to aid your intuition and acceptance of this new construction.
6.1.4 THE GEOMETRIC PRODUCT FOR VECTORS ON A BASIS
When asked to evaluate the geometric product of two vectors a and b given in a coordinate
basis, we can simply e valuate their inner and outer products and add them. However, it
is more direct to expand the geometric product in terms of a sum of geometric products
of the coordinate vectors. We then need to establish what those basis products are.
Let us take an orthonormal basis {e
i
} inametricspaceR
n
. The geometric product of a
basis vector with itself evaluates to a scalar derived from the metric:
e
i
e
i
= e
i
· e
i
+ e
i
∧ e
i
= e
i
· e
i
= Q[e
i
, e
i
],
where we used either the inner product or the bilinear form Q of the metric space (see
Appendix A). In a Euclidean space
R
n,0
, this is of course simply equal to 1 for all orthonor-
mal basis vectors.
For two different vectors from the orthonormal basis, we get
e
i
e
j
= e
i
· e
j
+ e
i
∧ e
j
= e
i
∧ e
j
.
This does not simplify further, but it does show that e
i
e
j
= −e
j
e
i
when i = j.We
sometimes denote e
i
e
j
as e
ij
to show more clearly that it is a single element of the algebra.
This element has an unusual property:
e
2
ij
= (e
i
e
j
)(e
i
e
j
) = e
i
(e
j
e
i
) e
j
= −e
i
(e
i
e
j
) e
j
= −(e
i
e
i
)(e
j
e
j
) = −1.
(6.4)
Therefore the algebra of the real Euclidean vector space
R
2,0
contains an element e
12
that
squares to −1 under the geometric product! It is not the imaginary unit from complex
numbers, but a real 2-blade, representing a unit plane.
SECTION 6.1 THE GEOMETRIC PRODUCT FOR VECTORS 145
In a 2-D vector space, the element e
12
completes the algebra. Multiplying e
12
with e
1
reverts to something we already had:
e
12
e
1
= e
1
e
2
e
1
= −e
2
e
1
e
1
= −e
2
(e
1
· e
1
),
so this is simply a multiple of e
2
. For the 2-D Euclidean space R
2,0
with orthonormal
basis, the full multiplication table is:
1 e
1
e
2
e
12
1 1 e
1
e
2
e
12
e
1
e
1
1 e
12
e
2
e
2
e
2
−e
12
1 −e
1
e
12
e
12
−e
2
e
1
−1
Now we can use the linearity and distributivity to compute the geometric product of any
twovectors.Fora = a
1
e
1
+ a
2
e
2
and b = b
1
e
1
+ b
2
e
2
:
ab = (a
1
e
1
+ a
2
e
2
)(b
1
e
1
+ b
2
e
2
)
= a
1
b
1
(e
1
e
1
) + a
2
b
2
(e
2
e
2
) + a
1
b
2
(e
1
e
2
) + a
2
b
1
(e
2
e
1
)
= (a
1
b
1
+ a
2
b
2
) + (a
1
b
2
− a
2
b
1
) e
12
By the extension of these techniques, the geometric product can be computed for vectors
in n-dimensional space.
6.1.5 DIVIDING BY A VECTOR
Since the geometric product on vectors is invertible, a vector a should have an inverse.
This inverse a
−1
is easy to find:
inverseofavector: a
−1
=
a
a · a
=
a
a
2
. (6.5)
This indeed works, for
a
−1
a =
1
a · a
aa=
1
a · a
a · a + a ∧ a
=
1
a · a
(a · a + 0) = 1.
Vectors with zero norms (the null vectors of Appendix A) do not have inverses.
The associativity of the geometric product makes the inverse of a vector unique.Ifa
would also be an inverse of a, then a
a = 1. Now rig ht-multiply both sides by a
−1
, regroup
by associativity, and you get a
= a
−1
. Therefore, there is only one inverse.
1
1 Note that the inverse for the geometric product is the same we used as “an” inverse for the inner product in
Section 3.5.2; it was then not unique, but we conveniently picked one that would be useful in the wider context
that we have now reached.

146 THE FUNDAMENTAL PRODUCT OF GEOMETRIC ALGEBRA CHAPTER 6
Having the inverse allows us to divide by vectors, so that we indeed can retrieve x from
knowing the value of (xa) and a, as was our goal:
(xa) a
−1
= x (aa
−1
) = x.
This shows the necessity of the associativity property. We often prefer to denote this by
a division sign as (xa)/a, but note that the noncommutativity of the geometric product
implies that division is also noncommutative. So using the notation /a is permitted as
long as we remember that this means “division on the right by a.”
Geometrically, the inverse of a vector a is a vector in the same direction as a, and properly
rescaled.
6.1.6 RATIOS OF VECTORS AS OPERATORS
Having an algebraic definition of the division of vectors already helps to solve geometric
problems. In a 2-D Euclidean space
R
2,0
, we can pose the similarity problem illustrated
in Figure 6.2:
Given two vectors a and b, and a third vector c (in the plane of a and b), determine
x so that x is to c as b is to a (i.e., solve x : c = b : a).
It is geometrically intuitive what we would want: a proportionality involving both the
relative length and angle of b and a should be transferred to x and c.
We take a leap of faith, and read this ratio in terms of the geometric product. So we guess
that the solution to this might be the solution to the equation
xc
−1
= ba
−1
.
The solution is immediate through right-multiplication of both sides by c:
x = (ba
−1
) c.
(6.6)
x
c
b
a
Figure 6.2: Ratios of vectors.
SECTION 6.2 THE GEOMETRIC PRODUCT OF MULTIVECTORS 147
This is a fully computable expression. For instance, with a = e
1
(so that a
−1
= e
1
),
b = e
1
+ e
2
, and c = 2e
2
in the standard orthonormal basis, we obtain x = ((e
1
+
e
2
) e
−1
1
)2e
2
= 2(1 − e
1
e
2
) e
2
= 2(e
2
− e
1
). Draw a picture like Figure 6.2 to convince
yourself of the correctness of this outcome.
In fact, we might see (ba
−1
) in (6.6) as an operator that acts on c to produce x.The
operator is parametrized by a and b, and it should be capable of both rotation and scaling
to produce x from c. From the construction above, we would suspect that it only depends
on the relative angle and size of the vectors a and b. If that is so, we may as well take a to
be the unit vector e
1
and b = ρ (cos e
1
+ sin e
2
), with ρ the relative length and the
relative angle (from a to b). Then we compute that the rotation/scaling operator is
ba
−1
= ρ (cos e
1
+ sin e
2
) e
1
= ρ (cos − sin e
12
).
You may verify that ba
−1
acts on the basis vector e
1
to produce ρ (cos e
1
+ sin e
2
),
and on e
2
it yields ρ (cos e
2
− sin e
1
). Moreover, since the geometric product is linear,
these results can be used to produce the result on a general vector c = c
1
e
1
+ c
2
e
2
, which
yields the x of our problem:
x = ρ (c
1
cos − c
2
sin ) e
1
+ ρ (c
1
sin + c
2
cos ) e
2
.
(6.7)
This is precisely the solution we would expect to the original problem, if we would have
expanded it in coordinates. It is clearly a rotation combined with a scaling. You would
represent it in terms of a matrix operation as
x
1
x
2
=
ρ cos −ρ sin
ρ sin ρ cos
c
1
c
2
, (6.8)
when expressed on the {e
1
, e
2
} basis.
It is highly satisfactory that our geometric product not only produces this result, but that
it does so in the form (6.6): x = (b/a) c. That expression is immediately derivable from
the original problem statement and completely formulated in terms of the elements of
the problem, rather than using an extraneous coordinate system. If you have to write
code, that is how you would want to specify it in a high-level programming language for
geometry; in comparison, (6.7) and especially (6.8) feel like assembly code, with their use
of coordinates reminiscent of registers.
The coordinate-free operator b/a is a good example of the kind of operational power that
the geometric product gives us. We will have much more to say about such operators in
Chapter 7.
6.2 THE GEOMETRIC PRODUCT OF MULTIVECTORS
In the definition of the geometric product for vectors, we followed a geometric motivation
and defined it in terms of inner product and outer product, loosely following its histor ic
