Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

SECTION 7.7 THE PRODUCT STRUCTURE OF GEOMETRIC ALGEBRA 199

through the versor product to again provide drawable elements. There is therefore never

a doubt about the geometrical nature of any of the multiplicatively constructed elements.

A similar contrast exists between Grassmann algebra, which permits arbit rary addition,

and what we called subspace algebra in our early chapters, permitting only the multiplica-

tive constructions. Unfortunately, mathematics has developed the additive Grassmann

and Clifford algebras to a much greater extent than their multiplicative parts. Much of

that work is irrelevant to their geometrical usage. It may even be incomplete, for what

would have been good and useful geometrical theorems may not be stated because they

are not generally valid when addition is allowed, and therefore are considered less pure.

When consulting the mathematical literature, be on the lookout for results on “simple”

multivectors, which require factorizability by the outer product (and are therefore about

blades) or the geometric product (and are thus about versors).

The sole exception we have been forced to make so far to our multiplicative principle

involves exponentiation. When one multiplies two rotors, a rotor results. Starting from

rotors that can be represented as the exponentials of 2-blades, we can construct the

exponentials of general bivectors as geometrically signiﬁcant operators. Permitting their

logarithm as an operation in our algebra, we should therefore permit general addition of

bivectors as a constructive operation—but the resulting elements may then subsequently

only be used for exponentiation. As such, this is still our multiplicative principle, merely

expressed in logarithmic for m.

In the grade approach to geometric algebra, the multiplicative principle is much less

easily formulated. The direct translation from the subspace product motivation would

permit us only to use the grade parts that deﬁne those products; that is the limited set

exposed in Section 6.3.2. Beyond that, there may be more geometrically relevant gr ades

(such the minimum and maximum grade of a geometric product that we will meet in

Section 21.7), but the general issue of admissible grades in the multiplicative principle

has not yet been thoroughly explored.

The mult iplicative principle is beginning to be acknowledged by mathematicians.

It will be interesting to see whether this will unearth hitherto dormant results in Clifford

algebra with patently geometrical applications. For now, we have made the multiplicative

principle the basis of our implementation (and it is part of the reason why it is among

the fastest known). We have not yet encountered geometrical situations that we cannot

represent and process.

7.7.3 BUT—IS IT EFFICIENT?

The use of blades as elements of computation and of rotors as operators to perform

orthogonal transformations on them permits us to encode a lot of geometry in a compact,

coordinate-free, and universal manner. As a consequence, we need to distinguish fewer

data types in geometric constructions. That in turn simpliﬁes the ﬂow of algorithms.

The resulting code looks a lot more compact and readable, since all operators can be

200 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

encoded in terms of geometrical elements of the application, rather than in unrelated

coordinate systems. But is that code also more efﬁcient?

This question is not easily answered. There are many facets to the issue because there

are many different kinds of operations in a geometry, and the balance may differ per

application. When we do a practical comparison for a ray tracer in Part III (see Table 22.1),

the fastest implementation of geometric algebra is 25 percent slower than an optimized,

explicitly written-out classical implementation. That cost of geometric algebr a is about

the same as the performance that can be achieved by the currently commonly used

homogeneous coordinates and quaternions (which provide much less universality than

geometricalgebra).Webelievea5to10percentoverheadfortheuseofgeometric

algebra should be achievable in such applications. This would be an acceptable price

to pay for the much cleaner structure of the code, with a much reduced number of

data types and an elimination of the corresponding special operations that need to be

explicitly deﬁned on them.

Let us brieﬂy discuss some of the relevant issues in making an efﬁcient implementation

of geometric algebra, with special emphasis on the orthogonal transformation of blades,

which will be the structural backbone of geometric modeling in Part II.

•

For the composition of orthogonal transformations, rotors are superior in up to

10 dimensions. The geometric algebra of an n-dimensional space has a general

basis of 2

elements. Rotors, which are only even-dimensional, in principle require

n−1

parameters for their speciﬁcation (though typical rotors use only a part of this).

Linear transformations speciﬁed by matrices need n × n matrices with n

parameters (and typically need them all). Rotors are therefore more efﬁcient for

storage of transformations in less than 7 dimensions (and for the practical dimen-

sionalities of 3, 4, 5 about twice as efﬁcient). Composing transformations as rotors

takes 2

operations, and composing them as matrices requires n

operations. There-

fore in fewer than 10 dimensions, rotors are more efﬁcient than matrices (in the

practical dimensions 3, 4, 5 about four times more). The reason for this gain by

rotors in composition is partly that they do not represent general linear transfor-

mations, just the orthogonal transformations, and that they can really exploit that

algebraic limitation, whereas matrices cannot. Unit quaternions are rotors in 3-D,

and of course well known to be efﬁcient for the composition of rotations.

•

For the linear transformation of vectors, matrices are always supe rior. To perform

an n×n matrixonann-dimensional vector (orthogonal or not) takes n

operations.

A general rotor could require as much as 2

n−1

× n × 2

n−1

= n 2

2(n−1)

in a straight-

forward implementation of its two-sided product. This is always more, in the

practical dimensions about four times more. Part of the computations can be

saved by realizing that grade-preservation of the rotor operation must mean that

some terms cancel (so that they do not need to be computed). Other techniques

may reduce the computation further, but not enough to make the direct rotor

approach competitive. The conversion of a rotor to a matrix may therefore be

SECTION 7.8 FURTHER READING 201

an advantageous way to apply it to a vector. This is what one typically does for

the unit quaternions, which are 3-D rotors; we treat their conversion matrix in

Sections 7.10.3 and 7.10.4.

•

For the linear transformation of general blades, outermorphism matrices beat

vector matrices and rotors. A general k-blade is speciﬁable on a





-dimensional

basis.Whenwewantto transforma k-blade byan orthogonaltransformation,wehave

three possibilities: rotors, outermorphism matrices (see Section 4.5), or matrices on

the constituentvectorsfollowed by recomposition.These take,respectively,





operations (using grade preser vation-based reduction),





operations, and kn





operations (the ﬁnal term is an estimate of the complexity of the outer product

construction). Of those three, the outermorphism matrix is cheapest (even for k = 1,

when it reverts to the vector matrix of the previous item). Thus the generalized linear

algebra that geometric algebra offers pays off in a different form.

•

For optimal orthogonal transformation, use rotors in a code generator. Although

outermorphism matrices are relatively cheap to use on k-blades, they are not the

optimum. They do not employ all the structure of the computation, for they use

neither the fact that the element to be transformed is a k-versor or a k-blade (rather

than a general k-vector), nor can they use our knowledge that the transformation

is or thogonal. Therefore they can still be improved by explicitly spelling out the

products involved for each speciﬁc type of multivector. If you can predict the

grade of the elements beforehand, such grade-based accelerations can be built in

at compile time. But even at run time it may be worth testing the multivector type

of an element and jumping to some specialized part of the code. This engenders

no overhead at all if you can predict and specify the multivector ty pe for each

variable in your code. In this approach, the rotor multiplication formula is crucial,

since it can be used by the symbolic code generator to derive all required formulas

in a uniﬁed manner.

The bottom line is: geometric algebra works, the structural simplicity it brings can be

used directly in high-level programming, and the computational overhead can be kept

low (in the order of 5-10 percent). But the actual low implementational level on which

the computations take place needs to be carefully designed, for a literal implementation

of the geometric algebra products can rapidly become too expensive. We devote Part

III of this book completely to these implementational issues.

7.8 FURTHER READING

In this chapter, most of the literature on the foundations of geometric algebra has

become accessible, and you might even read some of the mathematical literature on

Clifford algebra.

The obviously geometrically relevant literature on rotors (and spinors) has been absorbed

into geomet ric algebra so you can read about it in the language of this book. The basic

202 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

sources are [33] and [15], who also relate it to Lie groups in much more detail than we

do in this book. Other references about the actual use of rotors in geometric applications

will be supplied with the appropriate chapters in Part II.

For an entry to the more mathematical literature, we can recommend Clifford Algebras

and Spinors [41]. Together with [52] and [51], it gives the precise mathematics. Thoug h

all are short on actual geometry, they can be used to answer questions about the validity

of perceived patterns that one may be tempted to use in implementations.

7.9 EXERCISES

7.9.1 DRILLS

1. Compute R

≡ R

∧e

π /2

and apply to e

2. Compute R

≡ exp(e

∧ e

π/4) and apply to e

∧ e

3. Compute R

and apply to e

∧ e

4. Compute the axis and angle of R

5. Compute the product of the rotors R

π /2

and R

π /2

and apply to e

6. Reﬂect ( e

+ e

) ∧ e

in the plane e

∧ e

7. Reﬂect the dual plane reﬂector e

in the plane e

∧ e

7.9.2 STRUCTURAL EXERCISES

1. The generalization of the line reﬂection from axa

−1

to aXa

−1

seems straightfor-

ward when we remember that a k-blade can be written as the geometric product

of k mutually orthogonal vectors: X = x

···x

, and then simply compute

the outermorphism as (ax

−1

)(ax

−1

) ···(ax

−1

) = aXa

−1

. The result is

correct but the proof is wrong as it stands. Why? (Hint: Can you guarantee the

factorization after reﬂection?)

2. We have seen that for a Euclidean unit 2-blade, I

= −1. Interpret this geomet-

rically in terms of versors.

3. Verify that a line reﬂection in 3-D can be performed as a rotation. Which rotation?

Give the axis and angle. Verify that this reﬂection can be applied to any blade.

4. Show that the fact that the geometr ic product transforms naturally under applica-

tion of a versor, together with linearity, implies that the contraction is preserved.

(Hint: An intermediate step uses linearity to show that the outer product is

preserved.)

5. Show from the deﬁnition of the adjoint (in Section 4.3.2) that the adjoint of a

transformation that can be written as a versor product with a versor V is a versor

product with the versor V

−1

. Relate this to the orthogonality of a versor-based

transformation.

SECTION 7.9 EXERCISES 203

6. We can reﬂect mirrors into mirrors to compute the effective mirror of a total

reﬂection. Why can you ignore all signs in that computation and therefore

universally use M

for the reﬂection of mirror 1 in mirror 2 regardless of

whether they have been represented directly or dually?

7. Match the computation of the composition of 2-D rotations in Section 7.3.1 to

that of the 3-D rotations in Section 7.3.3, both algebraically and in the geometric

visualization.

8. To study the spherical image of rotation composition, take a rotation in the e

plane over π/2, followed by a rotation in the e

plane over π/2.Asrotors,

these are (1 − e

√

2 and (1 − e

√

2. Draw two great circles, w ith poses

corresponding to the rotation planes e

and e

. On these great circles, the

rotations over π/2 are represented as oriented arcs of length π/4 (the corresponding

rotor angle). These arcs are freely movable along their great circles. To compose

the rotations, make them meet so that you can perform R

and then R

. This is a

depiction as in Figure 7.6. The arc completing the spherical triangle is in a skew

plane with a length that looks like it might be π/3. Do an actual computation to

conﬁrm this value for the rotor angle and a plane of (−e

− e

+ e

√

The resulting rotation is over −2π/3 in this plane. Rewrite this using (7.10), and

show that the rotation axis is (−e

− e

+ e

9. Draw the rotated rotor R



as an arc in the spherical image. (Hint: What

would you expect it to be based on its geometric meaning? Warning: It is not

simply the R

arc rotated over the R

-arc!)

10. Establish the precise correspondence between the quantities in the rotor com-

position (7.9) and the quaternion product of (7.11). (Warning: This is a painful

exercise in keeping things straight, and not very rewarding.)

11. Derive the formulas for the reﬂection of a dual blade Y = X

∗

from the formulas

for reﬂection of a directly represented blade X. Derive the last column of Table 7.1

from the column before. Make sure you take the dual of both input and output

relative to the same unreﬂected pseudoscalar I

12. A special case of reﬂection is when A is the scalar 1. Derive the algebraic outcome

and interpret geometrically. Another special case is A = I

; compute that and

interpret. Why is the latter outcome not the dual of the former?

13. You can project onto a rotor and get a geometrically meaningful result. Give

the geometr ic interpretation of the projection P

[x] ≡ (xR) R

−1

. (Hint: Think

“chord.”) For rotors, it matters whether you put the inverse on the ﬁrst or the

last factor: what is (xR

−1

) R?

14. In

4,0

with the usual basis, perform a rotation in the e

∧ e

plane followed by

a rotation in the e

∧e

plane. Compute the rotor of the composition, and show

that this is the exponent of a bivector, not of a 2-blade. (Hint: See structural

exercise 5 of Chapter 2.) Note also that the rotor is not of the simple form “scalar

plus 2-blade” of Section 7.4 (or even “scalar plus bivector”).

204 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

7.10 PROGRAMMING EXAMPLES AND EXERCISES

7.10.1 REFLECTING IN VECTORS

The code of the ﬁrst example is a straightforward implementation of the line reﬂection

equation:

e3ga::vector reflectVector(const e3ga::vector &a,

const e3ga::vector &x) {

return _vector(a*x*inverse(a));

}

The program allows you to interactively manipulate both a (red) and x (green). You

can use the popup menu to switch to a mode that shows you that this also works for

bivectors.

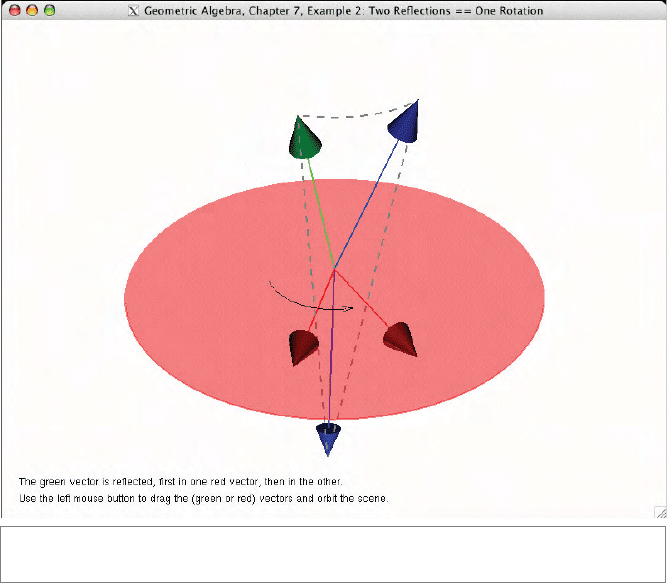
7.10.2 TWO REFLECTIONS EQUAL ONE ROTATION

This example displays an interactive version of Figure 7.2. The input vector (green)

is successively reﬂected in two different (red) vectors. The end result is that the input

vector is rotated, as expected. To reﬂect the input vector we invoke

reflectVector()

twice:

// update the reflected/ rotated vectors

g_reflectedVector = reflectVector(g_reflectionVector1,

g_inputVector);

g_rotatedVector = reflectVector(g_reflectionVector2,

g_reflectedVector);

Figure 7.9 shows a screenshot.

7.10.3 MATRIX-ROTOR CONVERSION 1

To connect to programs and libraries not based on geometric algebra (such as OpenGL),

you may need to convert back and forth between rotors and matrices. This example

provides the code for the 3-D case. The algorithms are based on geometric intuition—see

the next exercise for more efﬁcient solutions.

Rotor To Matrix Conversion

The columns of a (rotation) matrix are the images of the basis vectors under the

transformation. To convert from rotor to matrix, we transform e

, e

, and e

and copy

them into the matrix. The implementation is straightforward:

void rotorToMatrix(const rotor &R, float M[9]) {

// compute images of the basis vectors:

rotor Ri = _rotor(inverse(R));

e3ga::vector image[3] = {

_vector(R * e1 * Ri),

// image of e1

_vector(R * e2 * Ri), // image of e2

SECTION 7.10 PROGRAMMING EXAMPLES AND EXERCISES 205

Figure 7.9: Interactive version of Figure 7.2.

_vector(R * e3 * Ri) // image of e3

};

// copy coordinates to matrix:

for (int i=0;i<3;i++)

for (int j=0;j<3;j++)

M[j*3+i]=image[i].getC(vector_e1_e2_e3)[j];

}

Rotation Matrix To Rotor Conversion

Conversion from matrix to rotor is more complicated. Again we start with the fact

that the columns of the matrix are the images of the basis vectors. We should remember

that rotors are ambiguous: we can always increase the angle by 4π to get another rotor

that is equivalent. And since a rotation matrix does not specify the sense of rotation,

R and −R are both acceptable solutions. We compute the smallest rotor (i.e., with the

smallest angle) as our solution in three steps:

206 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

•

First, compute the smallest rotor R

that rotates e

to the image of e

under the

matrix transform.

•

Then, compute the smallest rotor R

that rotates R

to its image of e

under

the matrix transform. Because of orthogonality, this rotor will leave R

unchanged.

•

Finally, compute the full rotor: R = R

Because of orthogonality, e

automatically transforms correctly to R e

/R. The code for

this algorithm:

// note: very imprecise in some situations; do NOT use this

// function in practice

rotor matrixToRotor(const float M[9]) {

e3ga::vector imageOfE1(vector_e1_e2_e3,

M[0*3+0],M[1*3+0],M[2*3+0]);

e3ga::vector imageOfE2(vector_e1_e2_e3,

M[0*3+1],M[1*3+1],M[2*3+1]);

rotor R1 = rotorFromVectorToVector(_vector(e1), imageOfE1);

rotor R2 = rotorFromVectorToVector(_vector(R1 * e2 * inverse(R1)),

imageOfE2);

return _rotor(R2 * R1);

}

There is a compact formula that computes the smallest rotor that rotates a unit vector

a to another unit vector b,in3-D.Itis

R =

1 + ba



2(1+ b · a)

(7.23)

(We discuss it in more context in Section 10.3.2, but we use it now.) It is implemented

in the function

rotorFromVectorToVector(). The rotor formula is unstable when

a · b −1, which happens near a rotation over 180 degrees (the rotation plane is then

not accurately determined, neither geometrically nor algebraically). This also makes the

code listed above unstable. We work around this limitation in two ways in the stable

version of the function, shown in Figure 7.10. This ﬁrst is to pick the ﬁrst basis vector

such that a 180-degree rotation is not required. This is tested using

if(M[0*3+0]>

— 0.9f) {/*...*/}

. The second is to provide a default rotation plane (2-blade) to be

used by

rotorFromVectorToVector()—this plane must be orthogonal to the image

of the ﬁrst basis vector.

rotorFromVectorToVector() uses this plane in situations

where the rotation is near 180 degrees to come up with a solution for this geometrically

degenerate case.

7.10.4 EXERCISE: MATRIX-ROTOR CONVERSION 2

The conversion functions we presented above are (geometrically) intuitive, but they are

not the most efﬁcient solutions. A much better way is to perform the rotation on the

SECTION 7.10 PROGRAMMING EXAMPLES AND EXERCISES 207

rotor matrixToRotorStable(const float M[9]) {

e3ga::vector imageOfE1(vector_e1_e2_e3,

M[0*3+0],M[1*3+0],M[2*3+0]);

e3ga::vector imageOfE2(vector_e1_e2_e3,

M[0*3+1],M[1*3+1],M[2*3+1]);

e3ga::vector imageOfE3(vector_e1_e2_e3,

M[0*3+2],M[1*3+2],M[2*3+2]);

if (M[0*3+0]> — 0.9f)

{

rotor R1 = rotorFromVectorToVector(_vector(e1), imageOfE1);

rotor R2 = rotorFromVectorToVector(_vector(R1 * e2 * inverse(R1)),

imageOfE2,_bivector(dual(imageOfE1)));

return _rotor(unit_e(R2 * R1));

}

else if (M[1*3+1]> — 0.9f)

{

rotor R1 = rotorFromVectorToVector(_vector(e2), imageOfE2);

rotor R2 = rotorFromVectorToVector(_vector(R1 * e3 * inverse(R1)),

imageOfE3,_bivector(dual(imageOfE2)));

return _rotor(unit_e(R2 * R1));

}

else

{

rotor R1 = rotorFromVectorToVector(_vector(e3), imageOfE3);

rotor R2 = rotorFromVectorToVector(_vector(R1 * e1 * inverse(R1)),

imageOfE1,_bivector(dual(imageOfE3)));

return _rotor(unit_e(R2 * R1));

}

Figure 7.10: Rotation matrix to rotor conversion.

unit basis vectors symbolically and encode the results. This is straightforward. On an

orthonormal basis {e

}, with associated bivector basis e

≡ e

∧ e

,lettherotortobe

converted be

R = w + x e

+ y e

+ z e

The normalization of the rotor implies that w

+ x

+ y

+ z

= 1. Then one computes

R e



R = (w + x e

+ y e

+ z e

) e

(w − x e

− y e

− z e

)

= (w

+ x

− y

− z

) e

+ 2(−wz + xy) e

+ 2(wy + xz) e



1 − 2(y

+ z

)



+ 2(−wz + xy) e

+ 2(wy + xz) e

208 ORTHOGONAL TRANSFORMATIONS AS VERSORS CHAPTER 7

The transformation of the other basis vectors is obtained by cyclicity (resubstituting

the indices 1 → 2 → 3 → 1 and values x → y → z → x). The result is the matrix that

implements the linear transformation of applying the rotor R toavector:

[[ R]] =

⎡

⎢

⎣

⎡

⎢

⎣

1 − 2y

− 2z

2yx + 2wz 2zx − 2wy

2xy − 2wz 1 − 2z

− 2x

2zy + 2wx

2xz + 2wy 2yz − 2wx 1 − 2x

− 2y

⎤

⎥

⎦

⎤

⎥

⎦

This basically is also how one converts a quaternion into a matrix. If you already have

software for that, you can use it, though you may need to to initialize a rotor from its

(quaternion) coordinates, which i s the implementation of the correspondence of (7.10):

float w, x, y, z;

rotor R(rotor_scalar_e1e2_e2e3_e3e1, w, — z, — x, — y);

Here w, x, y, and z are the coordinates of a classic quaternion (which are not always

deﬁned in the same way, so beware what correspondence between the quaternion units

i, j, k, and the basis bivectors should be used!).

Implement this rotor to matrix conversion and test its speed when applied to vectors.

The example code provides the basic framework for testing and timing. In our solution,

this classic version was about four times faster than the geometric version.

The converse function, to convert a rotation matrix into a rotor, can also be sped up.

Here we can use the standard conversion of a matrix to a unit quaternion. Consider

the form of the matrix above and use combinations of the elements to retrieve the

four parameters. Addition of selected off-diagonal elements gives products of two of

the parameters; the diagonal elements can be added with appropriate signs to give the

square of only one variable, which is enough to compute the rest. Any trusted site on

quaternion computations gives the details.

7.10.5 JULIA FRACTALS

Fractals are usually introduced using complex numbers. But with the subsumption of

complex numbers into geometric algebra, as explained in Section 7.3.2, they are just

as easily generated using vectors in a real geometric algebra. This has the additional

advantage that they can be extended to more than two dimensions without changing

the algorithm. We explore this for Julia fractals, based on [37].

In the classic computation of 2-D fractal images, the image space is considered to be

a complex plane. Each pixel (indicated by its complex coordinates) is inside the fractal

set if, under repeated application of some mathematical function, the result does not

tend to inﬁnity.

For the Julia set, the complex function is an iterative computation, computing the

complex number X

k+1

as the p

power of the previous number and some additive

constant complex number C: