Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

SECTION 3.7 THE 3-D CROSS PRODUCT 87

(a) (b) (c)

a × b

a ∧ b

a × b

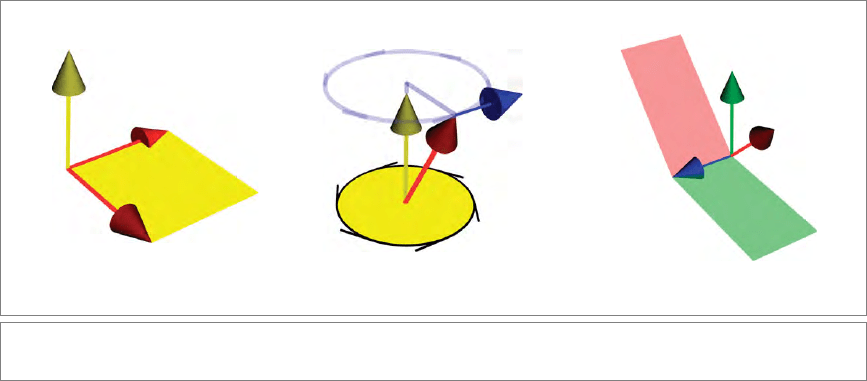
Figure 3.7: Three uses of the cross product.

as lines, or to other dimensions. You can also use it to intersect general lines in 2-D

through the embedding in homogeneous coordinates, but that’s about it.

All these uses have their limitations, and none extends easily to higher-dimensional

spaces. The cross product is, basically, a 3-D trick, and we need to replace it with some-

thing more universally applicable.

3.7.2 THE CROSS PRODUCT INCORPORATED

Let us take the characterization of the plane spanned by two vectors a and b as the deﬁning

example to redo the cross product with our subspace products. Using our subspace alge-

bra, we would characterize the plane by the 2-blade a ∧ b and the subspace normal to

it in the space with pseudoscalar I

by the orthogonal complement (a ∧ b)I

−1

.In3-D

Euclidean space

3,0

, the inverse pseudoscalar I

−1

equals −I

, and the orthogonal com-

plement is then indeed a vector, computed as (a ∧ b)

∗

= (b ∧ a)I

The classical method computes the normal vector as a × b. Both ways of computing the

normal vector must be equivalent, so we obtain a deﬁnition of the cross product in terms

of the outer product and contraction:

a × b = (a ∧ b)

∗

= (a ∧ b)I

−1

(3.28)

Note that this deﬁnition indicates explicitly that there are two geometrical concepts

involved in the cross product: spanning, and taking the orthogonal complement. The lat-

ter is related to the metric of the embedding space (since it ultimately contains the inner

product), and this makes the cross product a rather involved construction. In the next

chapter, we will see that it also makes its transformation laws complicated.

88 METRIC PRODUCTS OF SUBSPACES CHAPTER 3

Let us verify (3.28) by a coordinate-based computation in an orthonormal basis

, e

} for the 3-D Euclidean space R

3,0

.Leta = a

+ a

and b = b

+ b

. Then

a × b = (a

− a

) e

+ (a

− a

) e

+ (a

− a

) e

(3.29)

In (2.3), we have a coordinate expression for a ∧ b:

a ∧ b = (a

− a

) e

∧ e

+ (a

− a

) e

∧ e

+ (a

− a

) e

∧ e

It is easy to take the dual of this by using (e

∧ e

)(e

∧ e

) = e

and the like. The

result indeed agrees with the above.

So in terms of coordinates, we are computing very similar quantities whether we use a ∧b

or a × b.Yeta ∧ b is a simpler concept geometrically, because it does not depend on a

metric, and it is usable in n-dimensional space (not just 3-D). You used to be forced into

using the dual concept a × b since you could only treat vectors in standard linear algebra.

Now that we know that it is actually the dual of a bivector a ∧b, we had better not dualize

it and use a ∧ b “as is.”

This does not lose any geometry, for all computations with the cross product depicted in

Figure 3.7 can be recast into geometric algebra. Let us check them off:

•

Normal Vectors. We have just seen that a plane can be characterized directly by its

bivector rather than by a normal vector constructed from two vectors in it.

•

Velocities. For the velocity representation involving the cross product a×x, we note

that our algebra provides a suggestive rewriting through the duality properties:

a × x = (a ∧ x)

∗

= −(x ∧ a)

∗

= −xa

∗

= xA,

(3.30)

where A ≡ aI

is the 2-blade whose dual is a. This is depicted in Figure 3.8.

So we can replace the computation of the velocity of x during a rotation around

the axis a by a computation involving the rotation plane A. That actually works in

n-dimensional space (even in n = 2, where a rotation “axis” does not really exist!).

(From Chapter 7 onward, we will even be able to deﬁne a rotation in n-dimensional

space directly in terms of its rotation plane A,asexp(A).)

•

Intersecting Planes. The intersection of the two homogeneous planes of Figure 3.7(c)

can be written in terms of the bivectors as

a × b =



(AI

−1

) ∧ (BI

−1

)



I

−1

= (BI

−1

)



(AI

−1

)I



= (BI

−1

)A = (B

∗

)A.

We shall see (in Chapter 5) that this ﬁnal expression generalizes to intersections of

subspaces of arbitrary dimension as the

meet of B and A. That will be the algebraic

representation for the general incidence operator on subspaces.

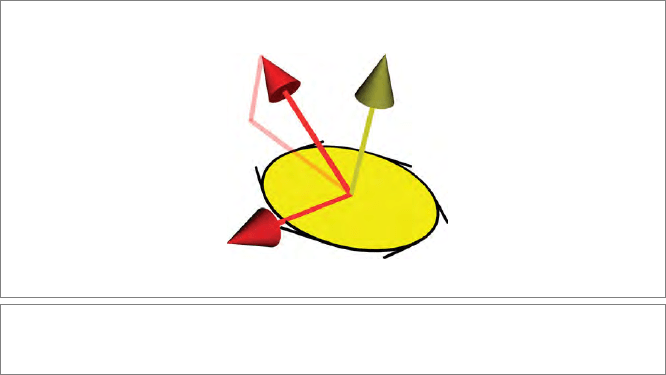
SECTION 3.8 APPLICATION: RECIPROCAL FRAMES 89

A=a

x⎦ A = a × x

Figure 3.8: The 3-D cross product a × x can be constructed as the contraction xA on the

dual A of a.

In summary, we can use our other products and the blades to replace the speciﬁc and

peculiar 3-D cross product on vector representations in a manner that works for all

dimensions. Therefore, we will do so. Apart from revisiting it in the context of linear

transformations in Chapter 4, where we ﬁnd more arguments against its use, we will not

employ the cross product any more (except occasionally to show the classical form of some

of our results). If you have used the cross product a lot, you may wonder what happened

to some of the identities that were useful in geometric computations (such as the bac-cab

formula). Structural exercises 10–12 show you what to substitute for them.

3.8 APPLICATION: RECIPROCAL FRAMES

Although we avoid using coordinates in our computations, they are often required to

present their results. We therefore need a way to retrieve the coefﬁcient x

of some vector

x, expressible as x =



on some basis {b

}

i=1

. If the basis happens to be orthonormal,

then this is simple: x

= x · b

, as is easily veriﬁed. However, we would like the ﬂexibility

to choose our bases arbitrarily to correspond to whatever the important directions are in

any given problem. We then need a more general expression.

Inametricspace

with chosen basis {b

}

i=1

and pseudoscalar I

= b

∧ b

∧···∧b

we can do this as follows. Associate with each basis vector b

a reciprocal basis vector b

deﬁned as

≡ (−1)

i−1

∧ b

∧···∧

∧···∧b

)I

−1

(3.31)

90 METRIC PRODUCTS OF SUBSPACES CHAPTER 3

Here the inverted arc denotes the removal of the vector b

, so this vector b

is the dual of

an (n−1)-blade spanned by all vectors except b

(as in (3.16)). The reciprocals of the basis

vectors form a basis {b

}

i=1

for the vector space.

The two bases {b

}

i=1

and {b

}

i=1

are mutually orthonormal, for

· b

= (−1)

j−1





∧···∧

∧···∧b

)I

−1



= (−1)

j−1

∧ b

∧···∧

∧···∧b

)I

−1

= δ

∧···∧b

)I

−1

= δ

I

−1

= δ

(3.32)

where the selector symbol δ

is deﬁned to be 1 when i = j, and 0 otherwise.

In spaces without an orthonormal basis, it is common to express the coefﬁcients of a

vector x by a superscript, so that x =



. (Some authors, like [15], then use a sum-

mation convention, in which summation is implied when the same index appears above

and below, but we will not employ it.) It is now straightforward to verify that x

= x · b

x · b

= (



) · b



· b

) =



= x

Therefore:

Even on a nonorthonormal basis, the coefﬁcie nts of a vector representation can be

computed by an inner product with appropriately chosen basis vectors.

It should be noted that orthonormal basis vectors have the same attitude as their

reciprocal:

= ±b

if {b

}

i=1

is an orthonormal basis,

with the + sign for positive vectors for which b

· b

=+1, and the − sign for negative

vectors for which b

·b

= −1. In a Euclidean metric space R

n,0

, the reciprocal basis vectors

therefore equal the basis vectors, and the distinction is merely notational.

Reciprocal frames are especially useful, as they allow consistent and convenient treatment

of nonorthonormal bases. These are known techniques from standard linear algebra. Usu-

ally, the reciprocal basis vectors are formulated in terms of minors of certain determinants.

It is satisfying to see how easily (3.31) deﬁnes the reciprocal basis as a geometrical con-

struction, namely as the orthogonal complement of the span of the other vectors. The

geometrically interpretable algebraic formula shows clearly that, for a general basis, the

coefﬁcient of b

depends on all vectors; for an orthogonal basis, it would only depend on

itself.

SECTION 3.10 EXERCISES 91

3.9 FURTHER READING

When reading other literature in geometric algebra, you will ﬁnd that most authors use

slightly different inner products. These alternatives are spelled out and compared in Sec-

tion B.1 of Appendix B. We maintain that the contractions are more pure mathematically

and geometrically, and they lead to fewer conditional computations in your code. That is

why we use them in this book.

We tried to convey their geometrical relevance for computer science in [17] (though with

limited success), inspired by [39] and [41]. The latter gives links to the mathematical

origins of the construction.

3.10 EXERCISES

3.10.1 DRILLS

1. Let a = e

+ e

and b = e

+ e

in a 3-D Euclidean space R

3,0

with orthonormal

basis {e

, e

}. Compute the following expressions, giving the results relative to

the basis {1, e

, e

∧ e

, e

∧ e

, e

∧ e

, e

∧ e

}. Show your work.

(a) e

a

(b) e

(a ∧ b)

(d) (2a + b)(a + b)

(e) a(e

∧ e

)

(f) a

∗

(g) (a ∧ b)

∗

(h) ab

∗

2. Compute the cosine of the angle between the following subspaces given on an

orthonormal basis of a Euclidean space:

(a) e

and α e

(b) (e

+ e

) ∧ e

and e

∧ e

+ sin ␾ e

) ∧ e

and e

∧ e

(d) e

∧ e

and e

∧ e

3. Set up and draw the reciprocal frame for vectors b

and b

on an orthogonal basis

, e

} represented as b

= e

and b

= e

+ e

. Use the reciprocal frame to

compute the coordinates of the vector x = 3e

+ e

on the {b

, b

}-basis.

3.10.2 STRUCTURAL EXERCISES

1. In 2-D Euclidean space R

2,0

with orthonormal basis {e

, e

}, let us determine the

value of the contraction e

(e

∧ e

) by means of its implicit deﬁnition (3.6) with

92 METRIC PRODUCTS OF SUBSPACES CHAPTER 3

A = e

and B = e

∧e

.LetX range over the basis of the blades: {1, e

, e

∧e

This produces four equations, each of which gives you information on the coefﬁ-

cient of the corresponding basis element in the ﬁnal result. Show that e

(e

∧e

) =

0 (1) + 0(e

) + 1(e

) + 0(e

∧ e

2. (continued from previous) Change the metric such that e

· e

= 0. This is a

nondegenerate metric, of which e

is a null vector (see Appendix A). Show that

you cannot now determine the coefﬁcient of e

in the value of e

(e

∧e

) through

the procedure based on (3.6). Then use the explicit deﬁnition of the contraction to

show that the contraction is still well deﬁned, and equal to e

(e

∧ e

) = e

3. Derive the following dualities for the right contraction, corresponding to (3.20) and

(3.21) for the usual (left) contraction:

C(B ∧ A) = (CB)A universally valid (3.33)

C(BA) = (CB) ∧ A when A ⊆C (3.34)

Then give the counterpart of (3.24). (Hint: use (3.19).)

4. Verify the geometric interpretation of the usual inner product between vectors, in

the light of viewing it as a speciﬁc example of the contraction. In agreement with

Section 3.3, show that x · a can be interpreted as an element of the 0-dimensional

subspace of a perpendicular to the subspace x.

5. The equation xα = 0 (in (3.8)) also has a consistent geometric interpretation

in the sense of Section 3.3. Since the scalar α denotes the point at the origin, xα

has the following semantics: the subspace of vectors perpendicular to x, contained

in the 0-blade α. Give a plausible correctness argument of this statement.

6. Similar to the previous two exercises, verify the geometric semantics of (3.7).

7. Duality in 1-D Euclidean space should avoid the extra sign involved in double dual-

ity, as speciﬁed in (3.24). Show this explicitly, by taking the dual of a vector a relative

to a suitably chosen unit pseudoscalar for the 1-D space and dualizing again.

8. We have seen in Section 2.4 how in 3-D space a trivector a ∧ b ∧ c can be written as

a ∧ b ∧ c = det([[abc]]

) e

∧ e

with [[ abc]] the 3×3 matrix having the three 3-D vectors a, b, c as columns (a con-

struction borrowed from standard linear algebra). Express this determinant fully in

terms of our subspace algebra.

9. In a plane with unit pseudoscalar I

, we can rotate a vector by a right angle using

the fact that contraction xI

is a perpendicular to x. Therefore, you can construct

an orthogonal basis for the plane from any vector in it. Use this capability to give a

coordinate-free speciﬁcation of a rotation of a vector x over ␾ radians in that plane.

Make sure you get the rotation direction correctly related to the plane’s orientation.

(We will do rotations properly in Chapter 7.)

SECTION 3.11 PROGRAMMING EXAMPLES AND EXERCISES 93

10. Using the deﬁnition of the cross product (3.28), verify that you can compute the

volume spanned by three vectors a, b, and c as a·(b ×c). What is the corresponding

formula using ∧ and ?

11. Derive the notorious bac-cab formula for the cross product (i.e., a × (b × c) =

b (a · c) − c (a · b)), directly from its deﬁnition (3.28). What is the corresponding

formula using ∧ and , and what is its geometric interpretation?

12. The inner product formula for cross products is (a × b) · (c × d) = (a · c)(b · d) −

(a ·d)(b ·c). Derive it from (3.28). What is the corresponding formula using ∧ and

, and what is its geometric interpretation?

13. In a nonorthonormal basis, the outer product b

∧b

of a vector and its corres-

ponding reciprocal is not generally zero. However, when summed over all basis

vectors, all those 2-blades cancel out:



∧ b

= 0.

(3.35)

Show this by expressing b

on the usual basis {b

}, and using a symmetry argument

on the resulting double summation.

3.11 PROGRAMMING EXAMPLES AND EXERCISES

3.11.1 ORTHONORMALIZATION

In this example we use the contraction product and the outer product to orthonormalize

a set of three vectors. The code is given in Figure 3.9, and Figure 3.10 shows a screenshot

void computeOrthoVectors(const e3ga::vector nonOrtho[3], e3ga::vector ortho[3]) {

// compute ortho vector 1:

// unit_e() returns a unit multivector (Euclidean metric)

ortho[0] = unit_e(nonOrtho[0]);

// compute ortho vector 2:

// << is the operator used for the left contraction

ortho[1] = unit_e(ortho[0] << (ortho[0] ^ nonOrtho[1]));

// compute ortho vector 3:

ortho[2] = unit_e((ortho[1] ^ ortho[0]) <<

(ortho[0] ^ ortho[1] ^ nonOrtho[2]));

}

Figure 3.9: Orthonormalization code (Example 1).

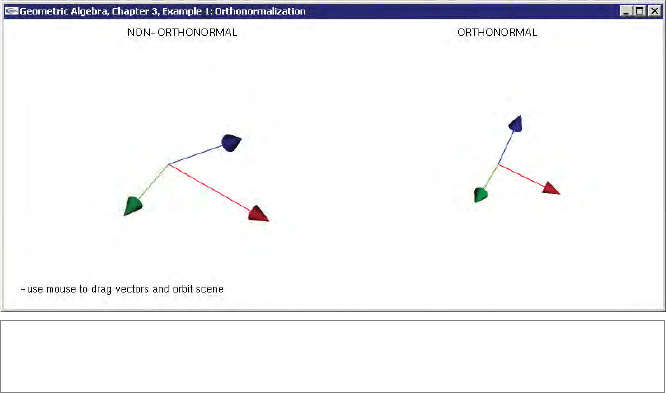
94 METRIC PRODUCTS OF SUBSPACES CHAPTER 3

Figure 3.10: Orthonormalization: nonorthonormal vectors on the left, orthonormal vectors

on the right (Example 1).

of its output. The ﬁrst vector is normalized using the function unit_e(). This function

takes any multivector and returns its unit in the sense that the Euclidean norm (sum of

the squares of all coordinates) is 1.

unit_e() assumes that its input is nonzero.

The second vector is computed in two steps. First, the bivector containing the ﬁrst two

vectors is computed. Then, the ﬁrst vector is removed from the bivector using the left

contraction (the << operator), resulting in the second vector, orthogonal to the ﬁrst. This

is in fact a computation of the dual within the plane of the two vectors.

The third vector is determined by computing the trivector spanned by all three vectors and

removing the bivector spanned by the ﬁrst two vectors (this is duality in their common

space). In 3-D this step is actually redundant, as the third vector is fully determined by

the ﬁrst two vectors. It can be computed using dualization of the bivector or using the

cross product (see the next exercise). We will generalize this example to Gram-Schmidt

orthogonalization in programming exercise 6.7.2 of Chapter 6.

What happens when the input vectors become dependent?

3.11.2 EXERCISE: IMPLEMENTING THE CROSS PRODUCT

When you download the code for exercise 2 of this Chapter, you will ﬁnd that it contains

a bare-bones

crossProduct() function:

/// returnsaxb

e3ga::vector crossProduct(const e3ga::vector &a,

const e3ga::vector &b) {

// exercise: compute the cross product, return it:

return _vector(0);

}

SECTION 3.11 PROGRAMMING EXAMPLES AND EXERCISES 95

Fill in the function such that it computes the cross product, according to the method

of in Section 3.7. The function

dual() is available to compute the dual of multivectors.

If you need the pseudoscalar, use the constant

I3, or its inverse, I3i.

You can check that your implementation works by running the example: drag the input

vectors (red and green) around, and verify that the blue vector stays orthogonal to them.

3.11.3 RECIPROCAL FRAMES

In this example, we explore the construction of reciprocal frames as explained in

Section 3.8. The example program allows you to manipulate three vectors and see the

reciprocal frame of these three vectors. Drag the mouse (using any button) to change

the vectors and orbit the scene. When you play around with the example, note the

following:

•

When you make a vector longer, its reciprocal vector becomes shorter.

•

The reciprocal of a vector is always orthogonal to the other two vectors in the origi-

nal frame. The easiest way to verify this is by “orbiting” the scene, but you may want

to take it upon yourself to draw the orthogonal plane as an exercise.

Figure 3.11 lists the code to compute a reciprocal frame.

Note that the example code uses a class called

mv. In the code shown so far, we always used

specialized multivector classes such as

vector, bivector, and trivector. The general

multivector class

mv is required here because we have the need for variables that can hold

different multivector types. For example, in the following loop, the multivector

P holds

four types of values: ﬁrst a scalar, then a vector, then a bivector, and ﬁnally a trivector.

mvP=(i&1)? —1.0f : 1.0f; // = pow( — 1, i)

for (unsigned int j = 0; j < nbVectors; j++)

if (j != i) P ^= IF[j];

Working with general multivectors is not as efﬁcient as working with specialized

multivectors, but sometimes we cannot avoid them.

3.11.4 COLOR SPACE CONVERSION

The reciprocal frame algorithm can be used to do color space conversion. Common

conversions (e.g., RGB to YUV) are from one orthogonal frame to another, so that the

reciprocal frame is not really necessary. The following is an example when computing

the reciprocal frame is required.

Suppose you want to detect the light emitted by red, green, and blue LEDs in a digital

image. The colors of the LEDs are unlikely to be pure red, pure green, and pure blue

in the RGB color space. But it is possible to transform the color space such that the

LEDs do register as such coordinate directions. First, measure the RGB values of the

different LEDs in the digital image. Then, compute the reciprocal frame of these three

96 METRIC PRODUCTS OF SUBSPACES CHAPTER 3

/**

Computes the reciprocal frame ’RF’ of input frame ’IF’

Throws std::string when vectors in ’IF’ are not independent,

or if one of the IF[i] is null.

void reciprocalFrame(e3ga::vector *IF, e3ga::vector *RF, int nbVectors) {

// Treat special cases (’nbVectors’ equals 0 or 1)

// ... (not shown here)

// compute pseudoscalar ’I’ of space spanned by input frame:

mv I = IF[0];

for (unsigned int i = 1; i < nbVectors; i++) I ^= IF[i];

if (_Float(norm_r2(I)) == 0.0)

throw std::string("reciprocalFrame(): vectors are not independent");

// compute inverse of ’I’:

mv Ii = inverse(I);

// compute the vectors of the reciprocal framevector

for (unsigned int i = 0; i < nbVectors; i++) {

// compute outer product of all vectors except IF[i]

mvP=(i&1)? —1.0f : 1.0f; // = pow( — 1, i)

for (unsigned int j = 0; j < nbVectors; j++)

if (j != i) P ^= IF[j];

// compute reciprocal vector ’i’:

RF[i] = _vector(P << Ii);

}

return;

}

Figure 3.11: Reciprocal frame code (Example 3). Edited for readability: some code was removed at the beginning of the

function that dealt with special cases for which (

nbVectors < 2).

“color vectors” and use the reciprocal frame to convert the image colors. The code that

implements this is shown in Figure 3.12.

The example program lets you play around by sampling different color values and seeing

the result of the conversion in real time. Figure 3.13 shows an example.

You can sample colors at any point in the viewport, including the color-bar at the

top. The code that draws this bar is also based on the subspace algebra: A unit vec-

tor in the “white”direction in the color space is initialized, then the dual of this vector

is computed and factorized: