Дорожинський О.Л., Тукай Р. Фотограмметрія

Подождите немного. Документ загружается.

Розміщення матеріальної точки і визначається вектором η, фіксується

такими величинами^ η - геоцентричним радіусом, a

- прямим сходженням, δ

схиленням. Якщо ж хочемо зафіксувати її прямокутні координати у системі oxyz,

то маємо:

rcosacosS

= rsinacos£ (8.7)

z = rsin£.

Зворотне перетворення дає:

α = arctgj>/χ (θ<α<24

)

δ = arctg(z / л]х

+у

^) (- 90° <δ

90°) (8.8)

ijx

Екваторіальна система координат безперервно змінює своє розміщення через

вплив прецесії (рух осі власного обертання по коловій конічній поверхні; тоді точка

весняного рівнодення зміщується; загальна річна прецесія для Землі становить

50,3") та нутації (коливання земної осі чи осі Світу, зумовлені збуренням Сонця і

Місяця). Для того, щоб така система стала інерційною, її необхідно зафіксувати на

певну епоху Т

, якою прийнята епоха

= 2000,0.

Інерційна система координат

встановлюється каталогами координат зірок. У космічній фотограмметрії

використовують католог Смітсоніанської астрофізичної обсерваторії (SAOC),

створений на підставі спостережень більше ніж 250 тис. зірок.

Для фіксації положення точок земної поверхні інерційна система незручна,

бо треба вказати ще й час, якого стосуються ці координати. Адже через вплив

гравітаційних сил полюси Землі змінюють своє положення на поверхні планети.

Тому для Землі прийнята Грінвіцька геоцентрична система координат (рис. 8.9).

Тут початок 0 збігається з центром мас Землі, вісь oz скерована в середній

Північний полюс Землі, вісь ох лежить у площині геоцентричного Грінвіцького

меридіана та площині екватора. Вісь оу доповнює цю систему до просторової

прямокутної, як показано на рис. 8.9.

У літературі наводяться формули, за якими можна від істинних інерційних

координат α, δ зафіксованих на епоху t, перейти до грінвіцьких координат.

300

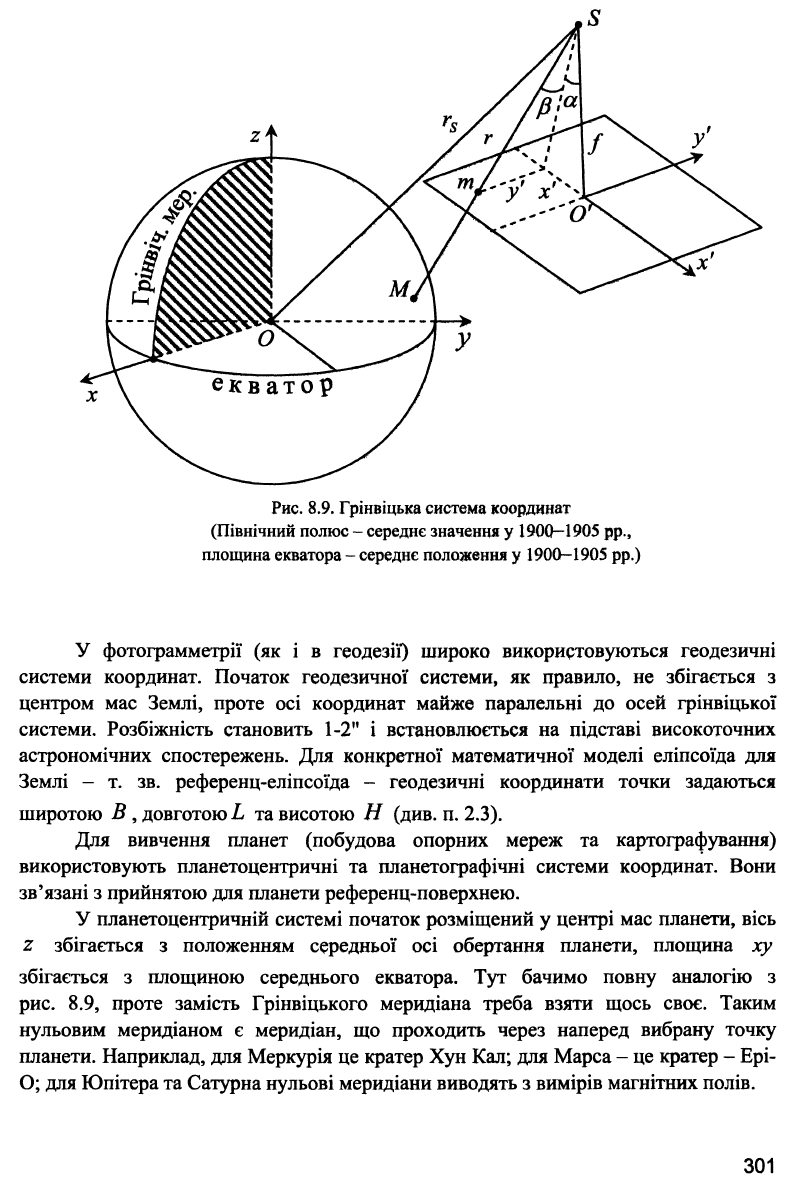
Рис. 8.9, Грінвіцька система координат

(Північний полюс - середнє значення у 1900—1905 pp.,

площина екватора - середнє положення у 1900-1905 pp.)

У фотограмметрії (як і в геодезії) широко використовуються геодезичні

системи координат. Початок геодезичної системи, як правило, не збігається з

центром мас Землі, проте осі координат майже паралельні до осей грінвіцької

системи. Розбіжність становить 1-2" і встановлюється на підставі високоточних

астрономічних спостережень. Для конкретної математичної моделі еліпсоїда для

Землі - т. зв. референц-еліпсоїда - геодезичні координати точки задаються

широтою В , довготою L та висотою Η (див. п. 2.3).

Для вивчення планет (побудова опорних мереж та картографування)

використовують планетоцентричні та планетографічні системи координат. Вони

зв'язані з прийнятою для планети референц-поверхнею.

У планетоцентричній системі початок розміщений у центрі мас планети, вісь

ζ збігається з положенням середньої осі обертання планети, площина ху

збігається з площиною середнього екватора. Тут бачимо повну аналогію з

рис. 8.9, проте замість Грінвіцького меридіана треба взяти щось своє. Таким

нульовим меридіаном є меридіан, що проходить через наперед вибрану точку

планети. Наприклад, для Меркурія це кратер Хун Кал; для Марса - це кратер - Ері-

О; для Юпітера та Сатурна нульові меридіани виводять з вимірів магнітних полів.

301

Планетоцентричні широти φ і довготи λ як сферичні координати зв'язані з

просторовими прямокутними координатами рівняннями, аналогічними до (8.7).

χ = r cos a cos λ

= rcos0?sinA (8.9)

ζ = r sin φ.

У літературі подаються формули для переходу від прямокутних координат

для стандартної епохи до прямокутних координат в описаній планетоцентричній

системі. Для цього використовують дані МАС (Міжнародного астрономічного

союзу) для кожної планети: координати північного полюсу обертання та напрямку

нульового меридіана (на епоху В 1950 або на епоху 2000).

Для картографування поверхні планет використовують планетографічну

систему. В ній положення точки задається широтою Φ\ довготою Л' та

висотою Η .

Планетографічна широта φ' - кут між нормаллю до референц-поверхні та

площиною екватора планети.

Планетографічна довгота Л' - кут, вимірюваний по екватору від нульового

меридіана до меридіана точки.

Планетографічна висота Η - віддаль по нормалі від точки до поверхні

референц-еліпсоїда.

Планетоцентричні та планетографічні координати обчислюють так:

tg<p =

л2

tg<p' =

{\-eftg<p', (8.10)

λ = 360° - Л' (для планет з прямим обертанням);

λ = Λ' (для планет з оберненим обертанням);

е -

- полярне стиснення;

а - екваторіальний радіус;

с - полярний радіус.

Згідно з рекомендаціями МАС для планет із прямим обертанням довготи

ростуть від 0° до 360° від нульового меридіана праворуч, а для зворотного

обертання - ліворуч.

302

8.3.4. Визначення планетоцентричних координат точок планети із

застосуванням кадрових систем

Кадрова знімальна система дає змогу отримати знімок (образ) як центральну

проекцію, в якій точка зображення визначається або прямокутними координатами

(х,у- /), або сферичними координатами (a

r) (рис. 8.9).

Отримуючи формули, що зв'язують точку т знімка з точкою Μ поверхні

планети, виходять з наявності вихідних даних, які можуть бути у різних

комбінаціях. Наприклад, можуть бути відомі кутові елементи орієнтації знімальної

камери в системі космічного апарата, або ж кутове орієнтування камери та

елементи орбіти в планетоцентричній системі координат на конкретну епоху

прецесійні елементи як відхилення епохи t від стандартної епохи 2000, чим

визначається положення нульового меридіану та Північного полюса планети.

Як видно з рис. 8.9, для точок S, т , Μ справедлива умова колінеарності;

тому за повною аналогією з аерозніманням запишемо класичні рівняння:

χ - . (8-Й)

(X-X

)a,+{Y-Y

%+{Z-Z

)c,

Ax-x

>2+(r-y

)b2+(z-z

(X-X

+(Y-Y

+(Z-Z

де X

- координати центра проекції у планетоцентричній системі;

Z - координати точки Μ на поверхні планети у цій самій системі;

і9

- компоненти матриці А (8.12), що описує поступовий перехід від

системи координат камери до планетоцентричної системи:

А = Α

ιο

, (8.12)

А = А

ΛΛ- (8.13)

Проміжна матриця А' (8.13) теж необхідна для обчислень. Тут кожна з

матриць А виконує певну зміну кутової орієнтації, а саме:

і9

,А

- матриці, що визначають положення нульового меридіана та

північного полюса обертання планети у поточний момент часу t; обчислюють за

рекомендованими даними МАС, що уже відзначалося раніше;

,А

- матриці, що обчислюють за прецесійними елементами як

відхилення епохи на момент знімання від стандартної епохи;

,А

- матриці, що обчислюють за елементами оскулювальної орбіти

космічного апарата на момент знімання; ці елементи визначають з формул руху

небесних тіл, вони виникають під впливом реального гравітаційного поля, впливу

303

Сонця та планет атмосферного гальмування, магнітного та теплового полів,

сонячної радіації;

ll9

- матриці, обчислені за кутовими елементами орієнтування

координатної системи космічного апарату у геоекваторіальній системі на момент

знімання;

,Л

- матриці, обчислені за кутовими елементами орієнтування

камери у координатній системі космічного апарата;

- матриця, що описує кутовий перехід θ від планетоцентричної

орбітальної системи до планетоцентричної екваторіальної системи (формула (8.3),

θ - істинна аномалія орбіти).

Якщо хочемо обчислити координати Χ,Υ,Ζ для точки Μ - поверхні

планет, то маємо такий вираз:

COS0

rsinacosfi

sin6

+ А

rsinp

-rcosacos β

де r

- віддаль від центра планети до космічного апарата (КА) (рис. 8.9);

визначається за параметрами орбіти на момент знімання.

Віддаль г як віддаль від космічного апарата до точки на поверхні планети

обчислюється, якщо відомі дані про рельєф планети. Якщо ж таких даних немає, то

беруть віддаль від КА до точки на референц-поверхні. У деяких випадках на КА

може працювати лазерний біддалемір, що безпосередньо вимірює таку віддаль.

Використання рівнянь колінеарності (8.8) у космічній фотограмметрії таке

саме, як і в аерофотограмметрії: вони становлять базу для космічної

фотогріангуляції (див. п. 8.4).

8.3.5. Визначення планетоцентричних координат точок планет із

використанням сканерних систем

Для отримання математичних залежностей необхідно брати до уваги

геометрію формування зображення. На рис. 8.10 маємо:

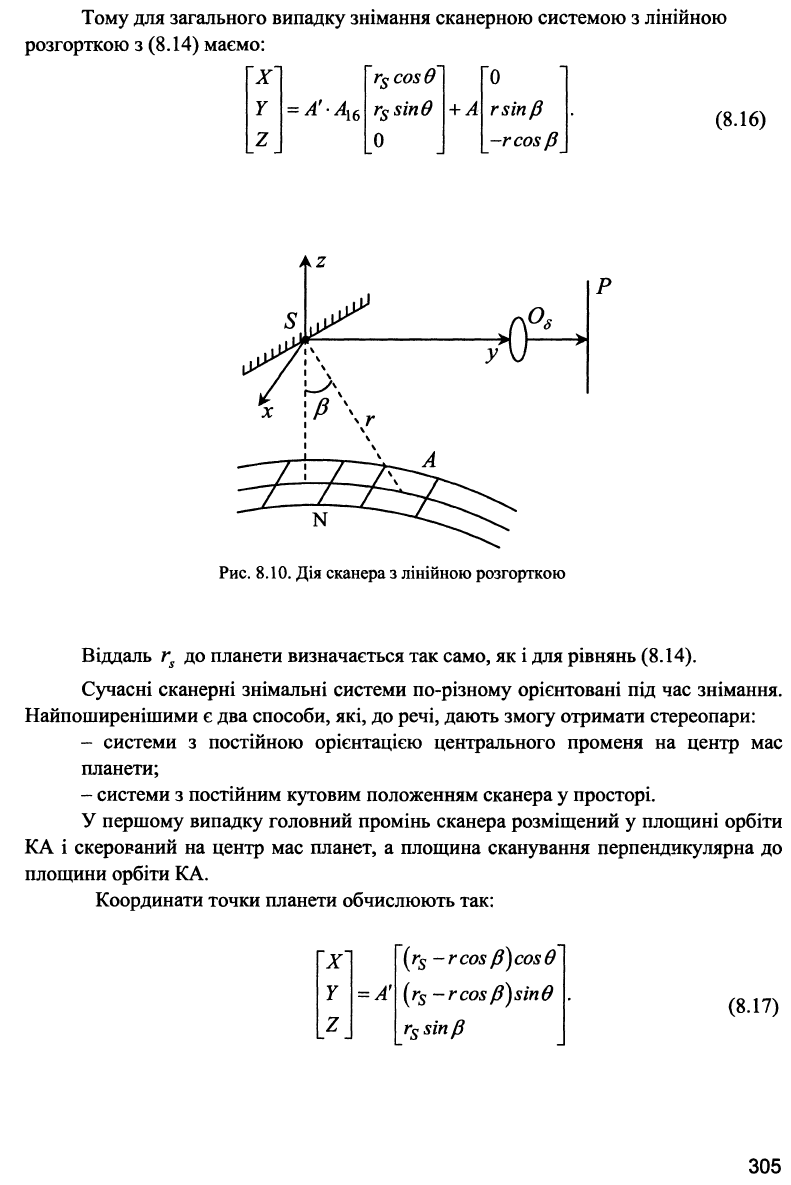
S - центр сканувального дзеркала, Ρ - площина зображення; Οδ -

об'єктив; N - піксел у надирі; А - боковий піксел у точці поверхні планети; β -

кут сканування; г - віддаль від сканера до точки планети.

Координати точки визначаються згідно з рис. 8.10 так:

rsin/?

-rcos/?

304

Тому для загального випадку знімання сканерною системою з лінійною

розгорткою з (8.14) маємо:

~X~

cos9

Y = A'-A

sin0

A rsinfi

-rcos β

(8.16)

Рис. 8.10. Дія сканера з лінійною розгорткою

Віддаль r

до планети визначається так само, як і для рівнянь (8.14).

Сучасні сканерні знімальні системи по-різному орієнтовані під час знімання.

Найпоширенішими є два способи, які, до речі, дають змогу отримати стереопари:

- системи з постійною орієнтацією центрального променя на центр мас

планети;

- системи з постійним кутовим положенням сканера у просторі.

У першому випадку головний промінь сканера розміщений у площині орбіти

КА і скерований на центр мас планет, а площина сканування перпендикулярна до

площини орбіти КА.

Координати точки планети обчислюють так:

'X'

Y = A'

-rcosp}cos6

- rcosP)sin6

rvSini

(8.17)

305

(Нагадуємо, що θ - кут, названий аномалією орбіти; це один із параметрів, що

характеризує орбіту

КА;

- довжина планетоцентричного радіус-вектора КА).

У другому випадку кутове орієнтування сканера {а - поздовжній, со -

поперечний кути та χ - кут розвороту) залишаються постійними.

Координати точки поверхні планет обчислюють так:

Υ = Α'·Α

^ · А

•

· А

•

Α β

де

, А

А =

матриці напрямних косинусів

cos

sin α 0" COS

sinfij 1

0 0

-sin α

cos α

0 1 0 ,Α

- 0 cos^ -sin^

0 1 -sin ω 0 COSfiJ 0 sin χ cos χ

"0 0 1" Ί

1 0 0

Α β =

cos β -

sin

0 1 0 0

sin β

cos/?

(8.18)

(8.19)

8.3.6. Визначення планетоцентричних координат точок планети з даних

радіолокаційного знімання

В останні роки набуло широкого поширення раділокаційне знімання поверхні

планети, зокрема Землі. При такому виді знімання є беззаперечні переваги, головна

з яких - це незалежність від атмосферного стану (задимленість, хмарність).

Радіопромені вільно проникають через атмосферу, а відбитий сигнал від поверхні

дає інформацію про радіояскравість елементарної поверхні. Положення точки

земної поверхні у просторі визначається віддаллю від радіолокатора до планети,

складовою швидкості та елементами осколювальної орбіти на момент знімання.

При зніманні планети в такому випадку вісь ζ

скерована в центр мас

планети, а антена радіолокатора відхилена від площини орбіти КА на заданий кут

ліворуч або праворуч.

З певних геометричних міркувань (рис. 8.11) та (8.14) можна отримати

формули для обчислення просторових координат точки поверхні планети:

-rcosp

Y = Α'·Α

-rsina

sin β

rcosa

sin β

де кути а

, β

показано на рис. 8.11.

306

Рис. 8.11. Сферичні координати (орієнтація координатної

системи)

при радіолокаційному зніманні

Тут: О - центр мас планет; Μ - точка поверхні планети; S - центр знімання на

момент знімання (час t); $

р>Ур>

р - планетоцентрична орбітальна система,

ρ>βρ - сферичні координати точки Μ; г - довжина радіуса-вектора точки Μ.

У (8.20) матриця А' обчислюється з виразу (8.19), матриця А

(як і раніше) є

такою:

cos θ - sin θ 0

sin θ cos θ 0 . (8.21)

0 0 1

Ав =

Взагалі кажучи, для створення коректної математичної моделі опрацювання

радіолокаційних зображень необхідно знати геометричні засади формування цих

образів. Наприклад, у фундаментальній монографії проф. Ю. Тюфліна [19]

згадується, що під час радіолокального знімання поверхні Венери були задіяні два

різні способи.

Перший, названий "смуговим зніманням", грунтувався на тому, що відбиті

від поверхні планет сигнали у межах вузької поверхневої смуги створювали один

рядок панорамного образу. Для кожного піксела смуги були відомі віддаль г, кут

та момент часу знімання t. За цими даними можна обчислити координати

точки планети в планетоцентричній орбітальній системі.

У другому способі для кожного елемента поверхні планет фіксується час

запізнення імпульсу τ (проходження радіоімпульсу до об'єкта і назад) та

доплерівське зміщення частоти ν, які зв'язані з віддаллю г та величиною

складової швидкості V

по напрямку на точку поверхні:

307

2 τ 2V

(8.22)

де c - швидкість світла; λ - довжина хвилі.

Ці дані дають змогу визначити координати точки планети у

планетоцентричній орбітальній системі координат.

Подамо приклад-схему знімання з використанням радара бокового бачення із

синтезованою апертурою SAR (англ. Synthetc Aperture Radar) на рис. 8.12 а, б.

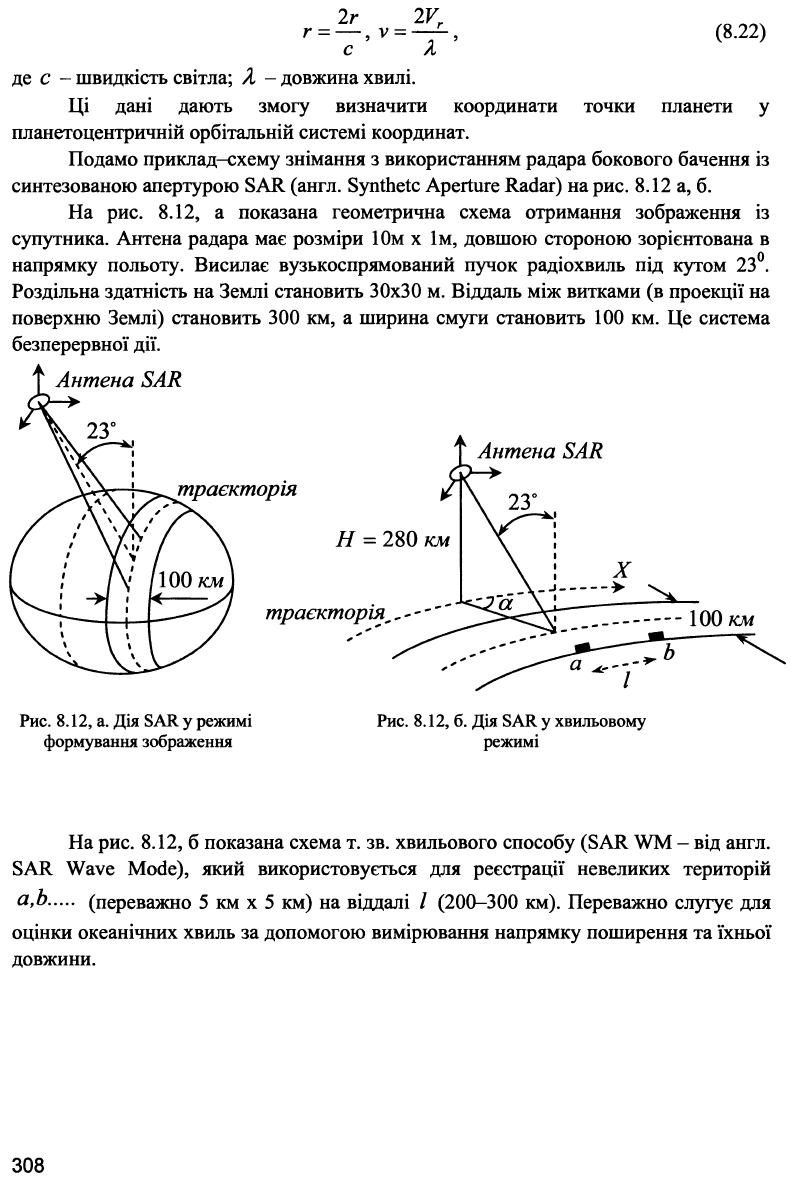
На рис. 8.12, а показана геометрична схема отримання зображення із

супутника. Антена радара має розміри 10м χ їм, довшою стороною зорієнтована в

напрямку польоту. Висилає вузькоспрямований пучок радіохвиль під кутом 23°.

Роздільна здатність на Землі становить 30x30 м. Віддаль між витками (в проекції на

поверхню Землі) становить 300 км, а ширина смуги становить 100 км. Це система

безперервної дії.

На рис. 8.12, б показана схема т. зв. хвильового способу (SAR WM - від англ.

SAR Wave Mode), який використовується для реєстрації невеликих територій

в>Ь (переважно 5 км χ 5 км) на віддалі / (200-300 км). Переважно слугує для

оцінки океанічних хвиль за допомогою вимірювання напрямку поширення та їхньої

довжини.

Рис. 8.12, а. Дія SAR у режимі

формування зображення

Рис. 8.12, б. Дія SAR у хвильовому

режимі

308

8.4. Космічна фототріангуляція

8.4.1. Математичні моделі космічної фототріангуляції

Основним завданням космічної фототріангуляції є створення мережі опорних

точок планети, а в низці випадків уточнення орбітальних та навігаційних

параметрів руху космічного апарату.

Для побудови мереж найбільш придатні кадрові знімки. Проте це не

виключає застосування сканерних та радіолокаційних знімальних систем.

Залежно від типу знімальної системи вхідними фотограмметричними

величинами є координати точки на знімку та елементи внутрішнього орієнтування

(для кадрових систем), координати точок на панорамному зображенні та масштабні

коефіцієнти (для сканерних систем), орієнтація радіолокаційного вектора - променя

- кути відхилення променя від планетоцентричного радіуса - вектора та віддаль до

точки планети (для радіолокаційних систем).

Види опорних даних у космічній фототріангуляції доволі різноманітні.

Частково про це згадувалось раніше, а зараз ще раз виокремимо найважливіші:

- координати центрів проекцій знімальної системи на момент знімання,

визначені в планетоцентричній геоекваторіальній системі певної епохи,

отримані з диференційних рівнянь руху космічного апарата;

- кутові елементи зовнішнього орієнтування зображень, визначені за

допомогою знімків зоряного неба та при відомих параметрах взаємного

розташування на космічному апараті знімальної системи та зоряної камери

(що фотографує зоряне небо);

- дані радіопрофілювання поверхні планети з космічного апарату;

- дані віддалемірних вимірювань від КА до поверхні планети (лазерні або

радіовіддалеміри);

- координати точок поверхні планети в планетоцентричній системі

координат, зафіксованої відносно тіла планети.

Можливі різні комбінації з цих опорних даних, і все залежить від конкретної

ситуації: від постановки задачі, мети, якої треба досягти, наявного апаратного

комплексу тощо.

Загальна математична модель достатньо добре описується рівняннями,

поданими в розділі 2, проте в кожній конкретній ситуації є свої особливості.

Покажемо це на прикладі фототріангуляції з одночасним визначенням початкових

умов руху супутника.

В основу фототріануляції покладено умову колінеарності для точки поверхні

планети Μ, точки зображення т та центру знімання S (рис. 8.9). Ця умова

описується рівняннями (8.11). Якщо задача сформульована так, як вказано вище, то

невідомими параметрами є:

309