Долгая М.В. Конспект лекций по дисциплине Основы компьютерной графики
Подождите немного. Документ загружается.

Министерство образования и науки Украины
Приазовский государственный технический университет
Факультет информационных технологий
Кафедра информатики
КОНСПЕКТ ЛЕКЦИЙ
по дисциплине
“Основы компьютерной графики ”
для студентов специальности 7.040302 «Информатика»
Мариуполь, 2010

2
УДК 004.92
Конспект лекций по дисциплине "Основы компьютерной графики” для студентов
специальности 7.040302 – Информатика / Составила Долгая М.В. - Мариуполь: ПГТУ, 2010- с.
Конспект лекций содержит 12 лекций по дисциплине "Основы компьютерной графики ”. В
лекциях рассматриваются основные алгоритмы компьютерной графики, такие как: преобразование
объектов на плоскости и в пространстве; виды проектирования; алгоритмы раз
ложения в растр
отрезков и окружностей; алгоритмы удаления невидимых поверхностей; алгоритмы построения
кривых и поверхностей методом В-сплайна.
Рецензенты: ст.преподаватель Алешин С.В.,
cт.преподаватель Матвиенко В.В.
Составитель ст. преподаватель Долгая М.В.
Ответственный
за выпуск доцент Чичкарев Е.А.
Утверждено на заседании ка
федры информатики
Протокол №_6
__ от “_22__” _декабря______2009г.
Рекомендовано учебно-методической комиссией факультета
информационных технологий
Протокол № __4
_ от “_ 6__” ___января_______2010г.
3
ЛЕКЦИЯ 1. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ
НА ПЛОСКОСТИ
В компьютерной графике рассматриваются четыре основных вида преобразований
объектов на плоскости и в пространстве:
- перенос;
- поворот;
- масштабирование;
- отражение.
Из курса геометрии известны представления перечисленных преобразований в виде
систем уравнений, задающих новые координаты точек по значениям их старых координат.
В общем случае для любых преоб
разований системы уравнений имеет следующий вид:
⎩
⎨
⎧
+=
′
+=
′
dycxy
byaxx
В частности, при выполнении переноса вдоль оси Х новые координаты определяются
из уравнений:
⎩
⎨
⎧
=
′
+=
′
yy
axx
Эти уравнения можно интерпретировать двояким образом:
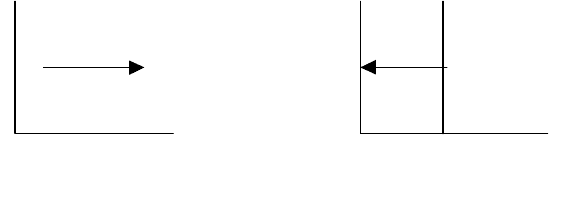
1. Все точки на плоскости ху перемещаются вправо на расстояние а–см. рис.1(а);
2. Координатные оси х и у перемещаются влево на расстояние а–см. рис. 1(б).
у у’ у
х, х’
о’ о
а
о х
Р а Р’
(а)
(б)
Рисунок1
(а)–перенос; (б)–изменение координат
В общем виде преобразование переноса выглядит так:
⎩
⎨
⎧
+=
′
+=
′
byy
axx
Преобразование поворота описывает система уравнений :
4
⎩
⎨
⎧
+=
−=
ϕϕ
ϕϕ
cossin'
sincos'
yxy
yxx
P’(x’, y’)
P(x, y)
ϕ
0
x
y
Рисунок 2 - Поворот вокруг точки О на угол
ϕ
Преобразование масштабирования описывает система уравнений :
⎩
⎨
⎧
⋅=
⋅=
ySy
xSx
y
x
'
'
,
где S
x
и S
y
масштабные множители.
Если S
x
и S
y
> 1, размеры объекта увеличиваются, то есть происходит растяжение, если
< 1 , сжатие. Но необходимо учитывать то, что так работает это преобразование при ситуации,
когда начальные координаты объекта заданы при расположении объекта в центре координат, то
есть, когда геометрический центр объекта точно или приближенно совпадает с началом
координат.
Преобразование отражения описывает система уравнений :
⎩
⎨
⎧
−=
−=
yy
xx
'
'
Компьютерная графика использует матричные формы записи этих преобразований:
- для переноса
[x’ y’] = [x y 1 ]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
ba
10
01
- для поворота
5
[x’ y’] =[x y]
⎥
⎦
⎤
⎢
⎣
⎡
−
ϕϕ
ϕϕ
cossin
sincos
- для масштабирования
[x’ y’] =[x y]
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
y
x
S
S
0
0
-для отражения
[x’ y’] =[x y]
⎥
⎦
⎤
⎢
⎣
⎡
−
−
y
x
0
0
Причем, можно использовать вариант записи координат, как в виде вектора-строки, так и в виде
вектора-столбца. Для преобразования поворота такая запись выглядит следующим образом:
⎥
⎦
⎤
⎢
⎣
⎡
−
=
⎥
⎦
⎤
⎢
⎣
⎡
ϕϕ
ϕϕ
cossin
sincos
'
'
y
x
⎥
⎦
⎤
⎢
⎣
⎡
y
x
Обозначим матрицу переноса через Т .
Т =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
ba
10
01
Для матрицы поворота введем обозначение R
R =
⎥
⎦
⎤
⎢
⎣
⎡
−
ϕϕ
ϕϕ
cossin
sincos
Матрицу масштабирования назовем S
S =
⎥
⎥
⎦
⎤
⎢
⎢
⎣
⎡
y
x
S
S
0
0
И, наконец, матрицу отражения обозначим как M
M =
⎥
⎦
⎤
⎢
⎣
⎡
−
−
y
x
0
0
.
Все приведенные записи геометрических преобразований описывают реализацию
соответствующего преобразования относительно начала системы координат на плоскости.
Чаще всего в графике приходится решать задачи, в которых преобразования не
ограничиваются одним каким-либо видом, а представляют собой некоторую последовательность
геометрических преобразований. Так, известно, что для вращения объекта вокруг заданной точки

6
с координатами не совпадающей с началом системы координат, необходимо реализовать
следующую последовательность преобразований: перенос системы координат для совмещения
начала координат с точкой, вокруг которой будет вращаться объект; поворот объекта вокруг точки
на заданный угол; возвращение системы координат в начальное положение. Используя выше
принятые обозначения матриц геометрических преобразований, данное преобразование можно
записать следующим об
разом:
[x’ y’] =[x y]
T
R
T
⋅
⋅
−1
Для перемножения матрицы переноса на матрицу поворота, как и для любого умножения матриц,
необходимым условием является равенство количества строк матрицы переноса и количества
столбцов матрицы поворота. Даже используя свойство ассоциативности матриц, то есть,
комбинируя перемножение,
(AB) C = A (BC)
мы сталкиваемся с тем, что матрица переноса имеет размер 3х2, а матрица поворота 2х2.
Следовательн
о, умножение их не может быть реализовано.
Для решения этой проблемы (и во многих других ситуациях) компьютерная графика использует
понятие однородных координат. Под однородными координатами понимают такую тройку чисел
Х
1,
Х
2
, Х
3 ,
для которых выполняется следующее соотношение:
3
2
3
1
X
X
X
X
=
Системы уравнений геометрических преобразований дополняются уравнением 1=1, а матричные
записи этих преобразований в однородных координатах обретают следующий вид:
Перенос - [x’ y’ 1] = [x y 1 ]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
1
010
001
ba
Поворот - [x’ y’ 1 ] = [x y 1 ]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
100
0cossin
0sincos
ϕϕ
ϕϕ
Масштабирование - [x’ y’1] =[x y1]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
100
00
00
y
x
S
S
Отражение - [x’ y’1] =[x y1]
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
−
100
00
00
y
x
Теперь все матрицы преобразований на плоскости имеют размеры 3х3, что позволяет выполнять
любые последовательности преобразований. Так, для примера поворота вокруг точки с
координатами ( x
0
, y
0
, ) эта последовательность реализуется путем выполнения следующих шагов:
1. Преобразование для переноса точки ( x
0
, y
0
, ) в начало координат О
7
[u
1
ν
1
1] = [x y 1 ] T
-1
где
T
-1
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−−
1
010
001
00
yx
2. Поворот на угол ϕ относительно нового начала координат О
[u
2
ν
2
1 ] = [u
1
ν
1
1] R
0
где
R
0
=
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
100
0cossin
0sincos
ϕϕ
ϕϕ
3. Перенос из начала координат в точку (x
0
, y
0
)
[x’ y’ 1 ]= [u
2
ν
2
1] T
где
T =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
1
010
001
00
yx
То есть, матрица преоб
разований для данной задачи определяется, как
R = T
-1
R
0
T
В результате получаем искомую матрицу, которая после выполнения двух матричных умножений
дает
R =
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−
1
0cossin
0sincos
21
cc
ϕϕ
ϕϕ
где введены обозначения
c
1
= x
0
- x
0
cjsϕ + y
0
sinϕ
c
2
= y
0
– x
0
sinϕ - y
0
cosϕ
8
ЛЕКЦИЯ 2. ГЕОМЕТРИЧЕСКИЕ ПРЕОБРАЗОВАНИЯ ОБЪЕКТОВ
В ТРЕХМЕРНОМ ПРОСТРАНСТВЕ
Перед рассмотрением геометрических преобразований объектов в трехмерном пространстве
вспомним некоторые понятия из векторной геометрии.
2.1 Векторы
Вектор – это направленный отрезок прямой линии, характеризуемый только его длиной и
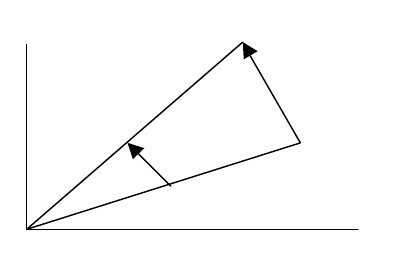
направлением. На рис. 1 показаны два представления одного и того же вектора a = PQ = b = RS .
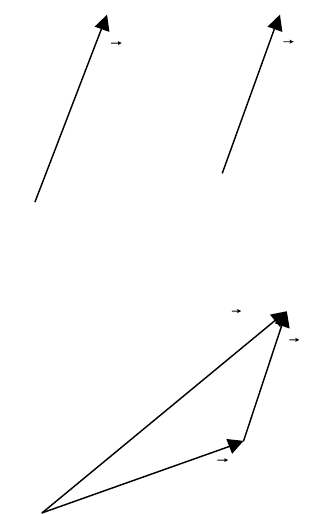
Следовательно, при переносе вект
ор не изменяется на рис. 2 начальная точка вектора b совпадает
с конечной точкой вектора a . Тогда сумма векторов a и b определяется как вектор c ,
проведенный из начальной точки вектора a в конечную точку вектора b , поэтому можно записать
c = a + b
P
Q
a
R
b
S
Рисунок 1 - Равные векторы
c
b
a
Рисунок 2 - Сложение векторов
Длина вектора a обозначается |a| и равна расстоянию между его начальной и конечной точками.
Вектор с нулевой длиной называется нулевым вектором и обозначается 0. Обозначение –a
применяется для вектора, имеющего длину |a| , направление которого обратно направлению
вектора a. Для любого вектора a и вещественного числа c вектор ca имеет длину |c| |a
| . Если a = 0
или с = 0, то ca = 0 , в противном случае вектор ca совпадает по направлению с вектором a , если с
> 0, или имеет противоположное направление, если c < 0. Для любых векторов u, v, w и
вещественных чисел c и k будем иметь
u + v = v + u
(u + v) + w = u + (v + w)
u + 0 = u
u + (-u) = 0
c (u + v) = cu + cv
(c + k) u = cu + ku
c (ku) =
(ck) u
9
1u = u
0u = 0
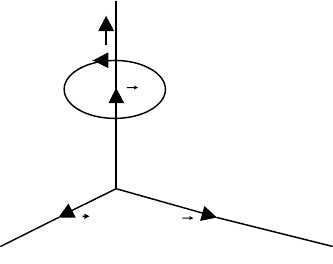
На рис. 3 показаны три единичных вектора i, j, k. Они взаимно перпендикулярны, имеют длину,
равную 1,и определяют направления координатных осей. Можно сказать, что векторы i, j, k
образуют тройку ортогональных единичных векторов. Координатная система является правой, это
означает, что если поворот от вектора i к вектору j на 90
0
соответствует повороту винта с правой
резьбой , то вектор k совпадает с направлением перемещения винта.
Точка О в начале координатной системы часто является начальной точкой всех векторов. Любой
вектор v может быть записан как линейная комбинация единичных векторов i, j, k
v = x i + yj + zk
i
j
O
z
y
x
k
Рисунок 3 - Прав
ая координатная система
Вещественные числа x, y, z определяют координаты конечной точки Р вектора v = OP. Этот
вектор v может быть обозначен либо в виде строки, либо в виде столбца
v=[x y z ] или
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
z
y
x
Числа x, y, z иногда называют элементами вектора v.
2.2 Геометрические преобразования в трехмерном пространстве
Если каждая точка P(x, y, z) отображается на точку P
/
(x
/
, y
/
, z
/
) в соответствии с уравнениями
⎪
⎩
⎪
⎨
⎧
+=
′
+=
′
+=
′
3
2
1
azz
ayy
axx
где a
1
, a
2,
a
3
– константы, то этот процесс называется переносом в трехмерном пространстве. Такой
перенос может быть записан в матричной форме
[]
[
]
Tzyxzyx 11
=
′
′
′

10
⎥
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎢
⎣
⎡
=
1
0100
0010
0001
321
aaa
T
Первая, вторая и третья строки матрицы Т соответствуют отображению бесконечно удаленных
точек на координатных осях, а четвертая строка – отображению точки [0 0 0 1] . Последнее
означает, что в однородных координатах точка [a
1
a
2
a
3
1 ] является отображением точки начала
координат О. Поворот вокруг координатных осей может быть описан матрицей без использования
однородных координат. Ради краткости так и будем поступать, обращаясь к однородным
координатам только в тех случаях, когда они действительно необходимы. Будем использовать
правую координатную систему, считая вращение вокруг оси положительным, если оно
соответствует положительному направлению эт
ой оси по правилу вина с правой резьбой. Это
показано на рис.4
y
x
z
Рисунок 4 - Вращение в положительном направлении вокруг координатных осей
Рассмотрим поворот вокруг оси z на угол α и для сокращения обозначим cos α = c и sin α = s .
Тогда можно записать
[]
[
]
Z
Rzyxzyx =
′
′
′
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
100
0
0
cs
sc
R
Z
В матрицу R
z
можно использовать для получения матриц R
x
и R
y
, определяющих поворот вокруг
соответствующих осей, чисто формальным образом, то есть без применения картинки. Это
делается путем циклических перестановок, получаемых заменой каждой из букв x, y, z на
последующую, считая, что за буквой z следует буква x .
Матрица R
z
превратится в матрицу R
x
циклическим переносом каждой строки на одну позицию и
затем выполнением аналогичной операции для столбцов:
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
−=
100
0
0
cs
sc
R
Z
⎥
⎥
⎥
⎦
⎤
⎢
⎢
⎢
⎣
⎡
− 0
0
100
cs
sc
