Долгая М.В. Конспект лекций по дисциплине Основы компьютерной графики
Подождите немного. Документ загружается.

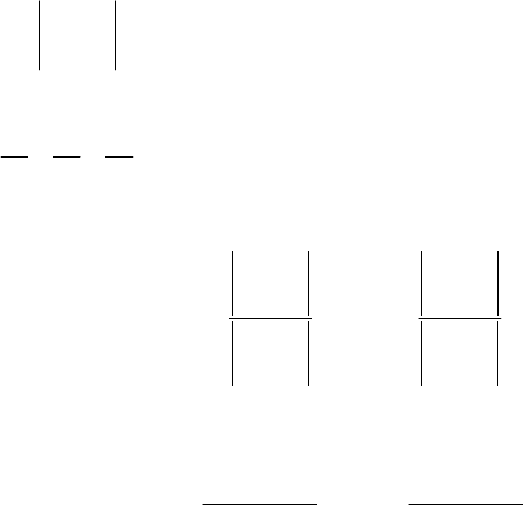
31
- найти точку отрезка прямой, в которой происходит изменение видимости;
- определить имеется ли непустое пересечение проекций двух многоугольников на
картинную плоскость;
- найти точку пересечения ребер объекта со сканирующей прямой;
- использовать результат в тесте принадлежности;
- найти точку пересечения граней объекта и прямой, соединяющей точку наблюдения
со специальной тестовой точ
кой в объектном пространстве.
6.1.2.1 Пересечение двух прямых
Мы договорились о том, что в АУНП будем рассматривать выпуклые объекты, ограниченные
плоскими гранями. Плоские грани, принадлежащие объектам, в свою очередь ограничены
ребрами, которые представляют собой отрезки прямых. Таким образом, объекты в
пространстве задаются координатами вершин, а точнее координатами начала и конца о
трезков,
то есть ребер принадлежащих граням объектов. Когда выполняется определение пересечений
прямых или отрезков, то рассматриваются пересечения их на плоскости, то есть после
проектирования этих ребер-отрезков на картинную плоскость. Вспомним немного школьную
геометрию. Как известно, прямые можно задать уравнениями
A
1
x + B
1
y +C
1
= 0
A
2
x + B
2
y +C
2
= 0
Если
11
22
0
AB
AB
=
, то прямые - параллельны,
если ,
111
222
A
BC
A
BC
==
, то прямые совпадают. Точка пересечения определяется по формулам:
11
22
11
22
i
CB
CB
x
AB
AB
=
и
11
22
11
22
i
AC
AC
y
AB
AB
=
или
12 21
12 21
i
CB CB
x
AB AB
−
=
−
и
12 21
12 21
i
AC AC
y
AB AB
−
=
−
.
Так как изначально объекты задаются координатами X,Y ребер, то есть отрезков прямых, то
коэффициенты уравнения прямых формируются из этих исходных данных.
21
12
12 12
A у y
Bx x
Cxyyx
=
−
=−
=− +

32
6.1.2.2 Пересечение двух отрезков
Алгоритм реализации этой задачи состоит из двух частей – определения пересечения прямых и
проверки принадлежности точки пересечения отрезкам. Первая часть выполняется, по
алгоритму 5.1.2.1 Заданы два отрезка значениями координат -
(
)
11 2 2
,
x
yxy и
()
'' ' '
11 2 2
,
x
yxy .
Отрезки, как уже говорилось, представляют собой ребра граней объектов. По значениям
координат начала и конца этих отрезков определяются уравнения прямых, которым они
принадлежат. Далее определяется, есть ли точка пересечения этих прямых? То есть, не
параллельны ли они и не совпадают ли. Если предыдущая проверка дала ответ – ложь, то
определяется точка пересечения
,
ii
x
y
. Но наличие этой точки не говорит о том, что
пересекаются собственно отрезки. Поэтому выполняется минимаксный тест принадлежности
точки пересечения отрезкам. Минимаксный тест реализуется с помощью следующего
логического выражения.
()
()
()
(
)
'' ''
12 1 2 12 1 2
max min , min min max , max
i
x
xxxx xx xx
⎡⎤⎡ ⎤
≤≤
⎣⎦⎣ ⎦
и
()
()
()
(
)
'' ''
12 12 12 12
max min , min min max ,max
i
yy y y y yy y y
⎡⎤⎡ ⎤
≤≤
⎣⎦⎣ ⎦
.
Если ответ на этот тест – истина, то точка пересечения прямых является точкой пересечения
отрезков, если – ложь, то отрезки не пересекаются.
6.1.2.3 Точка пересечения плоскости и прямой
Заданы:
- плоскость, проходящая через точки
()
()
()
,, , , , , , ,
iiii j jjj kkkk
Pxyz P x y z P x y z , причем, точки не коллинеарны и удовлетворяют
уравнению
0Ax By Cz D
+
++=;
- прямая, проходящая через точки
(
)
(
)
1111 2 222
,, , ,Pxyz иPxyz .
Что представляют собой эти точки в терминах исходных данных алгоритмов компьютерной
графики. Точки, задающие плоскость – это какие-либо три точки из всех вершин грани,
принадлежащей объекту. Элементарный вариант грани – треугольная грань, а значит в любом
случае как минимум для описания плоскости, содержащей грань, три точки в распоряжении
есть. Точки, задающие прямую – то
чки начала и конца ребра, ограничивающего какую либо
грань, которая в свою очередь принадлежит какому либо объекту. В данной ситуации
рассматриваются плоскости, содержащие грани одного объекта, а прямые, содержащие ребра,
других объектов. Конечная цель поиска точек пересечения - определения заслонения граней
одних объектов гранями других объектов.
Как известно, прямая, заданная координатами дву
х точек может быть представлена уравнением
111
cos cos cos
x
xyyzz
α
βγ
−
−−
==
,

33
где
21 2 1 21
cos ,cos ,cos
x
xyyzz
ddd
αβγ
−
−−
===
222
21 21 21
()( )()dxx yy zz=−+−+−.
Известно, что если
cos cos cos 0ABC
α
βγ
++=
, то плоскость и прямая параллельны.
Если
cos cos cos 0ABC
α
βγ
++= и
111
0Ax By Cz
+
+=
, то прямая лежит в
плоскости. Если предыдущие утверждения ложны, то есть точка пересечения, координаты
которой определяются из выражений
1
1
1
cos
cos
cos
i
i
i
xxt
yyt
zzt
α
β
γ
=
−
=−
=−
,
где
111
cos cos cos
Ax By Cz D
t
ABC
α
βγ
+
++
=
++
6.1.2.4 Проверка перекрытия 2-х выпуклых многоугольников в плоскости
изображения
Заданы:
два выпуклых многоугольника в плоскости изображения (проекции граней
трехмерных объектов).
Каждый многоугольник определен множеством вершин. F
1
и F
2
– многоугольники.
P
1,1
, P
1,2
…P
1,m
– вершины F
1
P
2,1
, P
2,2
…P
2,n
– вершины F
2
P
i,j
= (x
i,j
, y
i,j
), i – многоугольник, j – вершины
Многоугольник не перекрывается, если выполняется следующее minmax – ное условие:
Max (x
1,j
) < min (x
2,k
) или
max (x
2,k
) < min (x
1,j
) или
max (y
1,j
) < min (y
2,k
) или
max (y
2,k
) < min (x
1,j
)
Обычно требуются определить точки X граней. Могут существовать, по крайней мере, две
такие точки. Иначе многоугольник либо не перекрывается внутри. Как правило, начинается
проверка с теста пересечения, а не с теста принадлежности, т.к.
1. Вероятность пересечения больше вероятности полной вложенности или отсутствия
общих точек.
2. Отношение инцидентности
симметрично, а принадлежности -антисимметрично.
Поэтому принадлежность для обоих многоугольников, а пересечение достаточно для
одного из них.
3. Тест принадлежности включает вычисление X, а, следовательно, усложнения.
Так или иначе, перед определением точек X необходимо выполнить проверку minmax – ного
условия, дабы не усложнять в случае, когда они вообще не перекрываются.

34
6.1.3 Тест принадлежности(CT)
Применяется к объектам в картинно й плоскости.
Проверить: лежит ли точка P внутри многоугольника F, который является проекцией
грани объекта.
В элементарной геометрии существуют две процедуры проверки:
Первый вариант - по
∑
углов между лучами, соединяющими контролируемую точку и вершины
полигона.
Если
π2=
∑
i
α
, то точка принадлежит полигону,
если
0=
∑
i
α
, то точка не принадлежит полигону.
α
1
α
2
α
3
α
4
α
5
α
6
α
1
α
2
α
3
α
4
α
5
α
6
а) б)
Рисунок 1 – Определение принадлежности точки полигону по сумме углов
а)
π2
654321
=+++++=
∑
ααααααα
i
б)
0
654321
=−++++
α
α
α
α
α
α
Второй вариант – по подсчету числа, пересечений между ребрами полигона и
лучами, исходящими из контролируемой точки. Если точка внутри – число пересечений
нечетно, если вне – четно (при этом точка пересечения не должна совпадать с вершиной
полигона).
Рисунок 2 - Определение принадлежности точки полигону
по количеству пересечений
35
6.1.4 Тест глубины (DT)
Позволяет определить, какой объект заслоняет другие.
Сравниваемые элементы:
- точка и грань;
- две грани.
Глубиной называется расстояние между элементом и картинной плоскостью или между
элементом и точкой наблюдения. Глубина определяется по Z оси. Фактически представляет собой
сравнение Z координат 2-х элементов.
В машинной графике чаще всего используется три варианта теста глубины.
6.
1.4.1 Тест глубины 1 (DT1) :
(применяется к элементам объектного пространства).
Он определяет, заслоняет ли грань точку.
Для этого определяется:
- линия визирования, т.е. линия, соединяющая точку с точкой наблюдения;
- определяется точка пересечения линии визирования с гранью (IP);
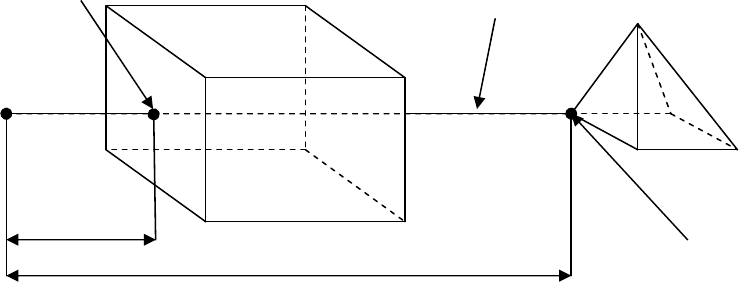
- расстояния: - от Т.З. до IР –dp;
- от Т.З. до контролируемой точки – dt;
Сравниваются dp
и dt.
В этой ситуации речь идёт о центральной проекции, т.е. когда есть конечная точка наблюдения.
Рисунок 3 – Тест глубины(DT1)
6.1.4.2 Тест глубины 2 (приоритетный тест)
Работает в алгоритмах использующих параллельную проекцию.
Работает с элементом, как в объектном пространстве, так и в картинной пло
скости
Элементы сравнения:
- точка и грань;
- две грани.
dt
Т.Н.
dp
Контролируемая
точка
IP
Линия визирования
36
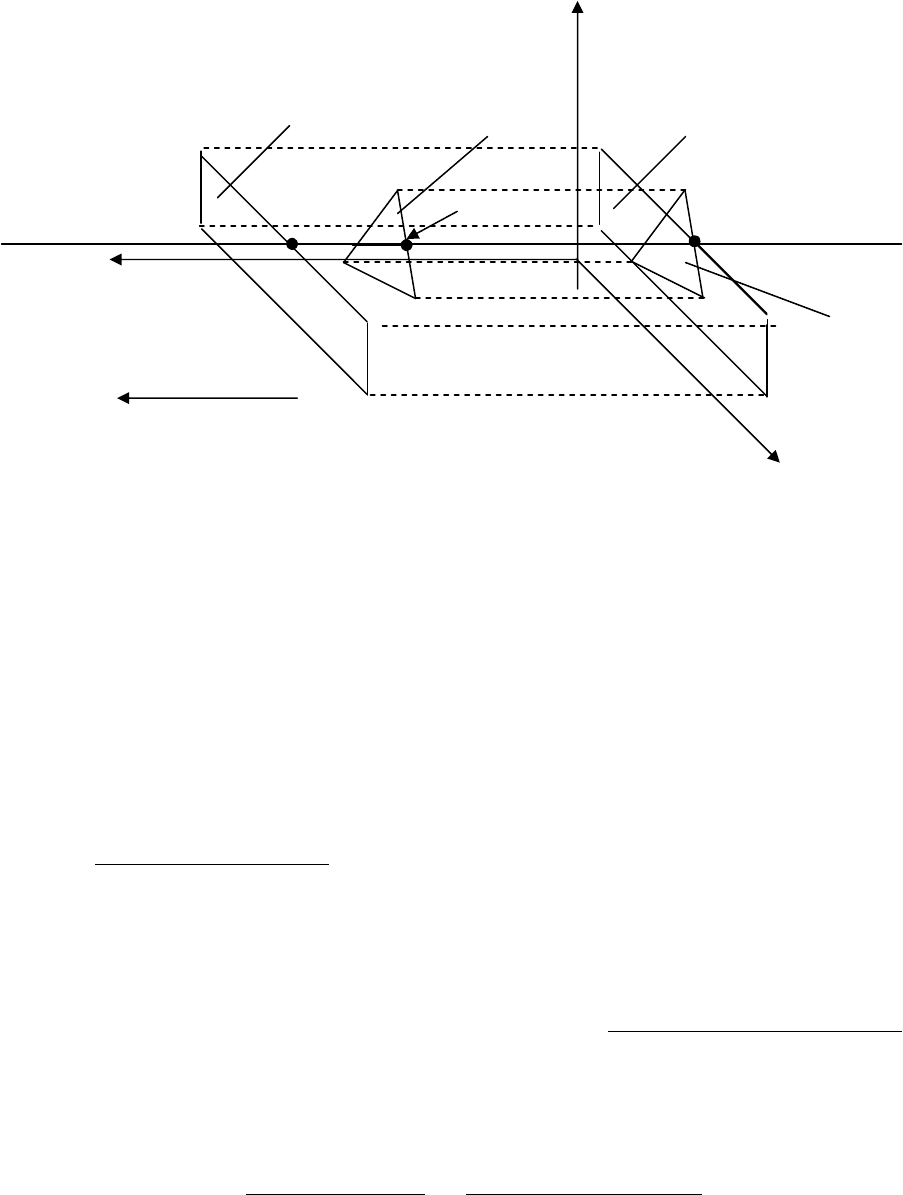
Рисунок 4 – Тест глубины (DT2)
G
1
и G
2
– две грани в объёмном пространстве.
Pr(G
1
) и Pr(G
2
) – проекции на картинную плоскость.
Р
12
– точка на картинной плоскости.
Точка Pr(G
1
) ∩Pr(G
2
).
1. Определяются точки P
1,2
2. Нахождение точек
Для этого: координаты P
1,2
(x
p
, y
p
) подставляют в уравнение плоскостей, содержащих грани G
1
и G
2
;
- уравнения плоскостей решают относительно z.
P
1
∈G
1
и P
2
∈G
2
P
1
и P
2
→ P
1,2
Получают z
1
и z
2
и сравнивают. Если z
1
> z
2
, то G
1
имеет относительный приоритет над G
2
.
Относительный приоритет:
Пусть p
r
(G
i
) и p
r
(G
j
) – проекции двух граней G
i
и G
j
.
Пусть P
i,j
= (x
p
, y
p
, 0) ∈ p
r
(G
i
)∩p
r
(G
j
)
Pi =(x
i
, y
i
, z
i
)∈G
i
и P
j
= (x
j
, y
j
, z
j
)∈G
j
и P
i
→ P
i,j
и P
j
→ P
i,j
, при условии, что x
i
= x
j
= x
p
и y
i
= y
j
= y
p
Тогда z
i
>z
j
, то G
i
имеет относительный приоритет над G
j
.
С помощью относительного приоритета можно определить монотонное упорядочение граней.
В случае точка – поверхность:
- определить уравнение плоскости, содержащее грань;
- в него подставить координаты точки;
- уравнение решить относительно z;
- найденное значение сравнивается с z координатой точки.
Если z
нов.
> z
точки
, то новая область с относительным приоритетом над точкой.
Если существуют проникающие грани
или циклические перекрытия - делят на две части.
X
G
1
G
2
Pr(G
1
)
Pr(G
2
)
P
1
P
1,2
Точка наблюдения
Y
P
2

37
Рисунок 5 – Тест глубины (DT2)
6.1.4.3 Тест глубины 3
Применяется в алгоритмах сканирующей прямой (будет рассмотрен в рамках алгоритма
сканирующей прямой).
6.1.5 Тест видимости (VT)
Применяется к объектам в объектном пространстве. Определяются потенциально видимые
грани, т.к. устраняются грани, заслоняемые самим объектом, т.е. задние грани.
Но потенциально видимые грани могут заслоняться другими объектами.
Определить:
- нормаль к грани (N);
- линия визирования, проходящая через точку наблюдения и основание L;
- вичислить угол
ψ
между N и L.
Грань потенциально невидима
,
если
2
π
ψ
≤
Грань невидима
,
если
2
π
ψ
f .
Т.к. угол
2
π
- критический угол, то достаточно вычислить скалярное произведение:
LN
NL
ψ
cos**
и проверить его знак.
Вектор нормали плоскости Ax + By + Cz + D = 0
n{A,B,C} и линия визирования L{e,m,n}
e = x
2
– x
1
m = y
2
– y
1
n = z
2
– z
1
n×L = A
1
×e + B×m + C×n
38
ЛЕКЦИЯ 7. ПРИМЕРЫ АЛГОРИТМОВ УДАЛЕНИЯ НЕВИДИМЫХ ПОВЕРХНОСТЕЙ
7.1 Алгоритм сканирующей прямой (Уоткинса)
Алгоритм оперирует в картинной плоскости. Изображение имеет вид набора
многоугольников, представляющих собой ортогональные проекции плоских граней 3-х
мерных объектов. Сканирующие прямые горизонтальные (т.е. параллельны оси Х).
Алгоритм состоит из двух частей:
1) нахождение пробных интервалов;
2) определение видимости.
Нахо
ждение пробных интервалов
Определяются отрезки сканирующей прямой, лежащие внутри каждого многоугольника.
Крайние точки этих отрезков - точки пересечения многоугольника и сканирующей прямой. Из
множества этих отрезков исключаются «изолированные», т.е. не перекрывающиеся, так как они
лежат на видимых частях проекций граней. Далее формируются пробные интервалы. Пробный
интервал – это отрезок сканирующей прямо
й, на котором видимость не изменяется. Для пробных
интервалов должны выполняться условия:
1) число отрезков, входящих в пробный интервал, постоянно и больше 1.
2) проекции на плоскость ХZ граней, соответствующих этим отрезкам не пересекаются.
Каждое такое пересечение обозначает начало нового пробного интервала.
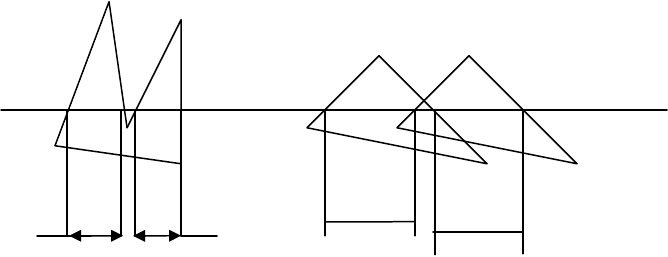
Рисунок 7.1
Определение отрезков сканирующей прямой внутри мн
огоугольников выполняется следующим
образом. Пусть Sij – отрезок сканирующей прямой, где i-номер многоугольника , а j-номер
отрезка для данного многоугольника. Если отрезки Sij на плоскости XY пересекаются для данной
сканирующей прямой, как это показано на рисунке 8.2, то в этой ситуации необходимо
определить, есть ли проникание граней.
F1
F2
F3
S21 S31
S11 S12
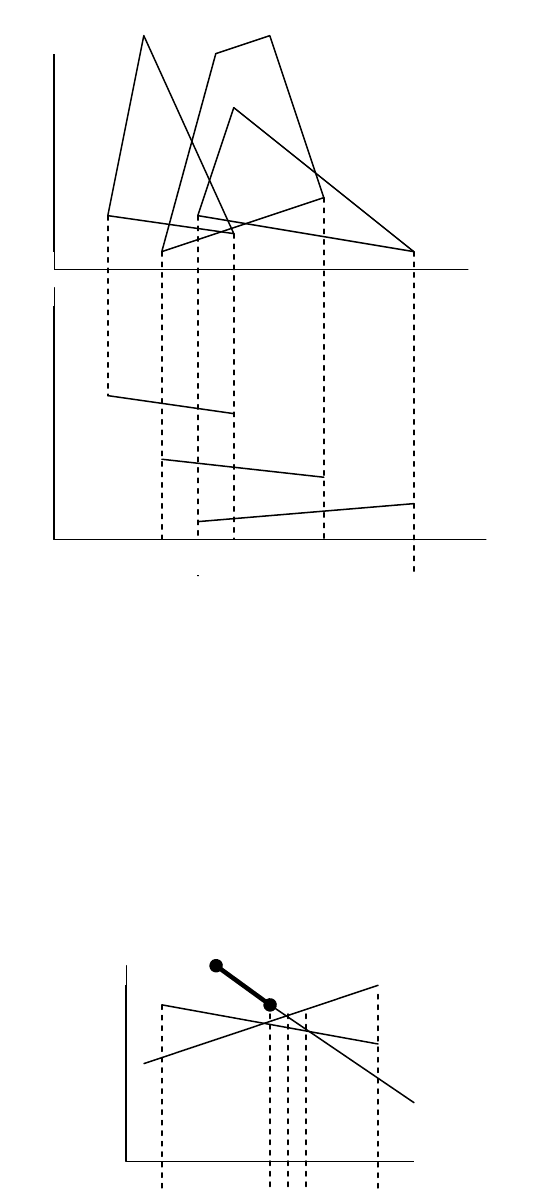
39
Рисунок 7.2
Для этого выполняется проецирование граней на плоскость ZХ и, если проекции на плоскость ZХ
не пересекаются, значит, нет проникания. В противном случае, точка пересечения является
точкой, которая разделяет полученный ранее отрезок на два новых пробных интервала.
Количество пробных интервалов в этом случае, естественно, увеличивается.
Определение видимости пробных интервалов
Во
прос о перекрытие отрезков на пробном интервале решается с помощью теста DTЗ -
сравнением Z координат отрезков на пробном интервале. Видимым является тот отрезок,
наименьшая Z – координата которого в пробном интервале больше или равна наибольшему
значению Z – координат всех других отрезков.
Рисунок 7.3
На рисунке 8.3 выделенный жирным - видимый отрезок, т.к. Zmin эт
ого отрезка больше Zmax
всех других отрезков в этом пробном интервале.
12 3 x
y
X
Z
Z
X

40
Видимость пробных интервалов при переходе от одной сканирующей прямой к другой
необходимо проверять в тех случаях, когда выполняется одно из следующих условий :
1) число отрезков на текущей сканирующей прямой отличается от числа отрезков на
предыдущей прямой;
2) изменилась связь крайних точек отрезков с ребрами проекции граней при переходе от
предыдущей сканирующей пр
ямой к текущей (в этом случае между сканирующими
.прямыми произошло пересечение двух ребер).
Функция стратегии
PM IS PM IS
Д
Т
