Doktorov E.V., Leble S.B. A Dressing Method in Mathematical Physics
Подождите немного. Документ загружается.


9.2 Kadomtsev–Petviashvili I equation—lump solutions 299
f
t
(k, ℓ)=4i(ℓ
3
−k
3
)f(k, ℓ). Therefore, the time dependence of the continuous
RH data is given by the simple formula
f(k, ℓ, t)=f (k, ℓ,0) exp
4i(ℓ
3
− k
3
)t
. (9.104)
To get discrete data evolution, we insert (9.84) with m
±
= 0 into (9.69). It
follows in the limit k → k
±
j
that
∂
t
k
±
j
=0. (9.105)
Finally, in the same limit, equation (9.89) gives
γ
±
j
(t)=γ
±
j
(0) + 12(k
±
j
)
2
t. (9.106)
9.2.6 Soliton solution
Algebraic solitons (lumps) of the KP I equation correspond to “reflectionless”
potentials when f(k, ℓ)=T (k, ℓ)=0.TheN-soliton solution is reconstructed
from (9.103) as
u
N
(x, y)=−2i∂
x
N
j=1
Φ
+
j
(x, y, t)+Φ
−
j
(x, y, t)
, (9.107)
where Φ
±
j
are found from the system of linear algebraic equations [see (9.102)]
1+iξ
±
j
Φ
±
j
+
N
i=1
′
(k
±
j
− k
+
i
)
−1
Φ
+
i
+(k
±
j
− k
−
i
)
−1
Φ
−
i
=0. (9.108)
In particular, equation (9.108) gives for N =1
Φ
±
1
=
i
∆
x − 2k
∓
1
y + 12(k
∓
1
)
2
t + γ
∓
1
(0) ±
i
k
+
1
− k
−
1
,
∆ =(X − 2k
R
Y )
2
+4k
2
I
Y
2
+
1
4k
2
I
.
The notations are
X = x − 12(k
2
R
+ k
2
I
)t − x
0
,Y= y − 12k
R
t − y
0
,k
±
1
= k
R
± ik
I
, (9.109)
x
0
=
k
R
γ
I
− γ
R
k
I
k
I
,y
0
=
γ
I
2k
I
,γ
±
1
(0) = γ
R
± iγ
I
.
With Φ
±
1
found, we obtain from (9.107) the on e-lump solution:
u
1
(x, y, t)=∂
2
x
ln ∆ =4
−(X − 2 k
R
Y )
2
+4k
2
I
Y
2
+1/4k
2
I
[(X − 2k
R
Y )
2
+4k
2
I
Y
2
+1/4k
2
I
]
2
. (9.110)

300 9 Dressing via nonlocal Riemann–Hilbert problem
This solution describes a smooth weakly localized (decaying as r
−2
)
configuration which moves uniformly with velocity v =(v
x
,v
y
) = [12(k
2
R
+
k
2
I
), 12k
R
]. For 2N noncoinciding eigenvalues k
±
j
, j =1,...,N,theN-lump
solution can b e compactly written in the form [354]
u
N
(x, y, t)=2∂
2
x
ln det B, (9.111)
where entries B
mn
of the 2N×2N matrix B are given by
B
mn
=(x − 2k
m
y + γ
m
)δ
mn
− i(1 − δ
mn
)(k
m
− k
n
)
−1
and the eigenvalues and normalization factors are arranged as
(k
+
1
,...,k
+
N
,k
−
1
,...,k
−
N
)and(γ
+
1
,...,γ
+
N
,γ
−
1
,...,γ
−
N
).
The solution (9.111) describes a process of collision of N lumps. It can be
shown [306] that (9.111) is decomposed into a sum of N o ne-lump solutions
for t →±∞. It is important that phase shifts of lumps stemming from their
mutual interaction are zero. This means that lump interaction is trivial.
9.2.7 KP I equation—multi ple pol es
Following Ablowitz and Villarroel [14, 439], consider here the case of a purely
discrete spectrum but assume that eigenfunctions can have multiple po les.
When a continuous spectrum is absent, the solutions M
±
of the RH problem
are the same, M
+
= M
−
= M. Suppose M(x, y, k) corresponds to the purely
discrete sp ectrum of the problem (9.68) and has 2N poles k
±
j
, j =1,...,N
with multiplicities r
±
j
:
M(x, y, k)=1+
2N
m=1
#
Φ
m
(x, y)
k − k
m
+
r
m
r=2
Ψ
m,r
(x, y)
(k − k
m
)
r
$
. (9.112)
Here Φ
m
= Φ
+
m
, m =1,...,N and Φ
m
= Φ
−
m
for m = N +1,...,2N.Tohave
explicitly the function M , we need know the Laurent coefficients Φ
m
and Ψ
m,r
.
Therefore, we derive first of all equations for them. Around the pole k
m
we
have
M(x, y, k)=ν(x, y, k)+
Φ
m
k − k
m
+
r
m
r=2
Ψ
m,r
(k − k
m
)
r
, (9.113)
where ν(x, y, k) is a regular part of M,andν → 1at|k|→∞.Nowweinsert
(9.113) into the equation (GM)(x, y, k) = 1. Expanding the Green function
up to the r
m
th order around k
m
and equating terms with equal powers of
(k − k
m
)
−r
, we obtain a system of integral equations
9.2 Kadomtsev–Petviashvili I equation—lump solutions 301
(GΨ
m,r
m
)(x, y, k
m
)=0,
GΨ
m,r
m
−1
+
∂G
∂k
Ψ
m,r
m
(x, y, k
m
)=0,
.
.
. (9.114)
GΦ
m
+
∂G
∂k
Ψ
m,2
+ ...+
1
(m − 1)!
∂
r
m
−1
G
∂k
r
m
−1
Ψ
m,r
m
(x, y, k
m
)=0,
Gν +
∂G
∂k
Φ
m
+
1
2
∂
2
G
∂k
2
Ψ
m,2
+ ...+
1
r
m
!
∂
r
m
G
∂k
r
m
(x, y, k
m
)=1.
The first equation in this system shows that the poles k
m
are indeed the dis-
crete data of the RH problem , while Ψ
m,r
m
are eigenfunctions corresponding
to the eigenvalues k
m
. It should be noted that equations (9.86) make up a
particular case of the system (9.114).
As in Sect. 9.2.1, we define the indices of poles
Q(k
m
)=
1
2πi
sign(Im k
m
)
D
dxdyuΦ
m
.
For bound-state eigenfunctions Φ
m
the orthogonality conditions are fulfilled:
Φ
−
ℓ
,Φ
+
j
=0,j= ℓ, (9.115)
where the scalar product is defined as
f,g =
1
π
D
dxdy
¯
f
x
g. (9.116)
The orthogonality conditions are easily obtained from the spectral equation
(9.68) for Φ
+
j
by multiplying it by
¯
Φ
−
ℓ
and integrating by parts. The indices
of the p oles can be expressed by means of this scalar product:
Q(k
+
j
)=
1
2πi
D
dxdyuΦ
+
j
= −
1
π
D
dxdy
2N
m=1
(∂
x
Φ
m
)Φ
+
j
=
1
π
D
dxdy
2N
m=1
(∂
x
¯
Φ
m
)Φ
+
j
=
2N
m=1
Φ
m
,Φ
+
j
= Φ
−
j
,Φ
+
j
.
Because f,g = −g, f, we get the important equality
Q(k
+
j
)=Q(k
−
j
). (9.117)
In what follows we shall restrict ou r con sideration to the simplest example
of a double p ole. In other words, we assume that the eigenfunction M(x, y)
has the following structure:
M(x, y, k)=1+
Φ
+
1
k − k
+
1
+
Φ
−
1
k − k
−
1
+
Ψ
2
(k − k
+
1
)
2
. (9.118)
302 9 Dressing via nonlocal Riemann–Hilbert problem
For determination of the Laurent coefficients Φ
±
1
and Ψ
2
we consider first the
function M near k = k
+
1
:
M(x, y, k)=ν
+
(x, y, k)+
Φ
+
1
(x, y)
k − k
+
1
+
Ψ
2
(k − k
+
1
)
2
, (9.119)
where ν
+
is regular in k
+
1
and tends to 1 at |k|→∞. In this case the system
(9.114) is reduced to three equations
(GΨ
2
)(x, y, k
+
1
)=0, (9.120)
GΦ
+
1
+
∂G
∂k
Ψ
2
(x, y, k
+
1
)=0, (9.121)
Gν
+
+
∂G
∂k
Φ
+
1
+
1
2
∂
2
G
∂k
2
Ψ
2
(x, y, k
+
1
)=1. (9.122)
In virtue of the similarity with equations (9.86), we can invoke the result
(9.89) and write by analogy
Φ
+
1
+iξ
+
1
Ψ
2
=0. (9.123)
As regards (9.122), we need the second derivative of the Green function that
is obtained from (9.87):
∂
2
G
+
∂k
2
=
2y − (x − 2ky)
2
G
+
+
x − 2ky
2π
. (9.124)
Substituting (9.87) and (9.124) into (9.122), we get
G
ν
+
+i(x − 2k
+
1
y)Φ
+
1
−
2iy +(x − 2k
+
1
y)
2
Ψ
2
(x, y, k
+
1
)
=1− Q(k
+
1
) −
1
2
q
2
+
1
2
(x − 2k
+
1
y)Q
2
, (9.125)
where
Q
2
=
1
2πi
D
dxdyu(x, y)Ψ
2
(x, y),q
2
=
1
2π
D
dxdy(x−2k
+
1
y)u(x, y)Ψ
2
(x, y).
(9.126)
Now we prove that Q
2
=0andq
2
= −Q(k
+
1
). Indeed, if Φ
+
1
∼ r
−α
1
and
Ψ
2
∼ r
−α
2
, then it follows from (9.121) written in a differential form as
(i∂
y
+ ∂
2
x
+2ik
+
1
∂
x
+ u)Φ
+
1
+2i∂
x
Ψ
2
=0
that α
2
= α
1
+ 1. Further, by analogy with the one-lump solution (9.110)
we suppose that u ∼O(r
−2
)atr →∞.Thenα
1
= 1. Hence, performing
integration for Q
2
in (9.126), we obtain in virtue of the decay rate of Ψ
2
Q
2
= −
1
2πi
D
dxdy(i∂
y
+ ∂
2
x
+2ik
+
1
∂
x
)Ψ
2
=0.

9.2 Kadomtsev–Petviashvili I equation—lump solutions 303
Taking then (x − 2k
+
1
y)Ψ
2
from (9.123) and inserting it into (9.125) gives
q
2
= −Q. Eventually, eliminating Φ
+
1
in (9.125) by means of (9.123), we can
write (9.122) as
(
G
ν
+
+
1
2
(ξ
+2
1
− 2iy + γ
+
2
)Ψ
2
)
(x, y, k
+
1
)=1−
1
2
Q(k
+
1
),γ
+
2
= γ
+
2
(t).
(9.127)
The inhomogeneous integral equation (9.127) will have a solution if the right-
hand side is orthogonal to the complex conjugated solution ¯χ of the adjoint
integral equation (9.81) (the Fredholm condition [425]). In the case of the
second-order pole in k
+
1
we get ¯χ(x, y, k
+
1
)=u(x, y)Φ
+
1
(x, y), in accordance
with (9.83). As a result, the Fredholm condition provides
0=
1 −
1
2
Q(k
+
1
)
D
dxdy ¯χ
=
1 −
1
2
Q(k
+
1
)
D
dxdyu(x, y)Φ
+
1
(x, y) ∼
1 −
1
2
Q(k
+
1
)
Q(k
+
1
).
Because we assume Q(k
+
1
) =0,thisgivesQ(k
+
1
)=2.
Now we will treat the simple pole k
−
1
, taking into account that Q(k
−
1
)=
Q(k
+
1
) ≡ Q =2.Neark
−
1
we write
M(x, y, k)=ν
−
(x, y, k)+
Φ
−
1
k − k
−
1
, (GM)(x, y, k)=1, (9.128)
and ν
−
is regular in k
−
1
and tends to 1 as |k|→∞. Let us remember that
for simple pole k
−
1
equations (9.86) exist, the second one of them being trans-
formed to (9.88). Because Q = 1, equation (9.89) is not valid and cannot b e
used to determine Φ
−
1
.
In order to have analog of (9.89) for Q = 1, we differentiate (GM )=1
(9.128) in k:
∂G
∂k
ν
−
+
G
∂ν
−
∂k
+
1
k − k
−
1
∂G
∂k
Φ
−
1
−
1
(k − k
−
1
)
2
GΦ
−
1
=0.
Expanding G and (∂G/∂k)neark
−
1
and collecting terms with equ al powers of
(k − k
−
1
)
−1
, we obtain the following integral equations:
(GΦ
−
1
)(x, y, k
−
1
)=0,
∂G
∂k
ν
−
+ G
∂ν
−
∂k
+
1
2
∂
2
G
∂k
2
Φ
−
1
k
−
1
=0.
Taking into account explicit formulas (9.87) and (9.124) for derivatives of the
Green function, we get
(
G
∂ν
−
∂k
+i(x − 2k
−
1
y)ν
−
−
1
2
(2iy +(x − 2k
−
1
)
2
)Φ
−
1
)
(x, y, k
−
1
)
=i(x − 2k
−
1
y)
1 −
1
2
Q
− q
0
−
1
2
˜η, (9.129)

304 9 Dressing via nonlocal Riemann–Hilbert problem
where
q
0
=
−1
2πi
D
dxdyu(x, y)ν
−
(x, y), ˜η =
−1
2π
D
dxdy(x − 2k
−
1
y)u(x, y)Φ
−
1
(x, y).
On the other hand, equation (9.88) gives for Q =2
&
G
ν
−
+i(x − 2k
−
1
y)Φ
−
1
'
(x, y, k
−
1
)=−1. (9.130)
Let us multiply (9.130) by −[q
0
+(1/2)˜η] and add it to (9.129). As a result,
we obtain an analog of (9.89) for the case Q =2:
∂ν
−
∂k
+iξ
−
1
ν
−
−
1
2
(2iy +(ξ
−
1
)
2
+ δ
−
)Φ
−
1
k
−
1
=0,δ
−
= δ
−
(t). (9.131)
Now we have all that is necessary to determine Φ
±
1
and Ψ
2
.Neark = k
+
1
ν
+
(k)=1+
Φ
−
1
k − k
−
1
.
and (9.123) and (9.127) give the following system of linear algebraic equations:
Φ
+
1
+iξ
+
1
Ψ
2
=0, 1+(k
+
1
− k
−
1
)
−1
Φ
−
1
+
1
2
(ξ
+2
1
− 2iy + γ
+
2
)Ψ
2
=0. (9.132)
Eliminating Ψ
2
, we o btain a relation between Φ
+
1
and Φ
−
1
:
1+
i
2ξ
+
1
(ξ
+2
1
− 2iy + γ
+
2
)Φ
+
1
+
Φ
−
1
k
+
1
− k
−
1
=0. (9.133)
Near k = k
−
1
ν
−
(k)=1+
Φ
+
1
k − k
+
1
+
Ψ
2
(k − k
+
1
)
2
and (9.131) gives
1+
1
k
−
1
− k
+
1
+
i
ξ
−
1
1
(k
−
1
− k
+
1
)
2
Φ
+
1
+
1
(k
−
1
− k
+
1
)
2
+
2i
(k
−
1
− k
+
1
)
3
Ψ
2
+
i
2ξ
−
1
[(ξ
−
1
)
2
+2iy + δ
−
]Φ
−
1
=0. (9.134)
Eliminating once again Ψ
2
, we obtain the second equ ation for Φ
+
1
and Φ
−
1
:
1+
1
k
−
1
− k
+
1
(
1+i
1
ξ
+
1
+
1
¯
ξ
+
1
1
k
−
1
− k
+
1
−
2
|ξ
+
1
|
2
1
(k
−
1
− k
+
1
)
2
)
Φ
+
1
+
i
2
¯
ξ
+
1
[(
¯
ξ
+
1
)
2
+2iy + δ
−
]Φ
−
1
=0. (9.135)
9.2 Kadomtsev–Petviashvili I equation—lump solutions 305
Hence, we have a system of two algebraic equations (9.133) and (9.135) to
determine Φ
±
1
and hence Ψ
2
from (9.132). Expanding M in the asymptotic
series in k
−1
leads to the reconstruction formula
u(x, y)=−2i∂
x
(Φ
+
1
+ Φ
−
1
)=2∂
2
x
ln ∆. (9.136)
To obtain evolution of the parameters γ
±
1
(t)andδ
−
(t), we substitute M found
above into (9.69) taken at r →∞.Thisgives
γ
±
1
(t)=γ +12k
±2
1
t, δ
−
(t)=δ − 24ik
−
1
t, γ, δ =const.
After rather lengthy but transparent calculations we obtain the function ∆ in
the form [439]
∆(x, y, t) (9.137)
=
&
[X − 2k
R
Y −12(k
2
R
− k
2
I
)t]
2
− 4k
2
I
(Y +12k
R
t)
2
+ δ
−
R
(t)
'
2
+
2(Y +12k
R
t)
&
1+2k
I
[X − 2k
R
Y −12(k
2
R
− k
2
I
)t]
'
+
γ
+
I
(t)
k
I
− δ
−
I
(t)
2
+
1
k
2
I
#
X − 2k
R
Y −12(k
2
R
− k
2
I
)t −
1
2k
I
2
+4k
2
I
(Y +12k
R
t)
2
+
1
4k
2
I
$
,
where X and Y were introduced in (9.109). The lump solution of the KP I
equation corresponding to the multiple p oles (9.118) is given by
u
ℓ
=2∂
2
x
ln ∆ =2
#
∆
XX
∆
−
∆
X
∆
2
$
.
Note that the existence of indices (topological charges) is stipulated by the
fact that the potential decays sufficiently slowly (algebraically) at infinity.
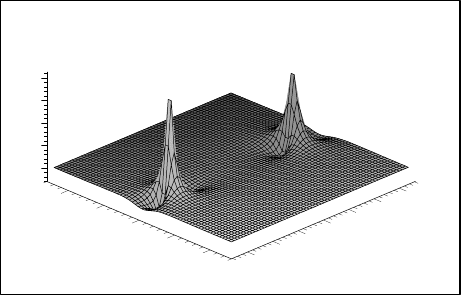
Villarroel and Ablowitz [439] investigated this solution for t →±∞.It
was shown that the solution decomposes in this limit into two humps each
having its own velo city. Figures 9.1–9.3 illustrate a typical scattering process
described by the solution (9.137). The interaction of the lumps can be treated
in terms of two-particle dynamics under the action of attractive force. Mutual
attraction is not strong enough to form a bound state. Hence, as distinct
from the N-lump configuration, interaction between multiple-pole humps is
nontrivial. These authors also considered more complicated versions of the
multiple-pole structure.
Note that a class of (in general, singular) solutions of the KP I equation
(and some other equations) with multiple poles was obtained by Dubrovsky
[136].

306 9 Dressing via nonlocal Riemann–Hilbert problem
Fig. 9.1. Lumps of the solution (9.137) before interaction. Z = X − 2k
R
Y − 12
(k
2
R
− k
2
I
)t, k
R
=1/2, k
I
=1,γ = δ = 0 [439]
9.3 Davey–Stewartson I equation
In the context of shallow water waves, the DS I equation
iq
t
+
1
2
(q
xx
+ q
yy
)+ǫ|q|
2
q = φ
x
q, (9.138)
φ
xx
− φ
yy
=2ǫ
|q|
2
x
,ǫ= ±1
describes the (2+1)-dimensional evolution of a small-amplitude, slowly mod-
ulated packet of surface waves with dominant surface tension [105, 470]. Here
Fig. 9.2. Interaction of lumps described by the solution (9.137) [439]
9.3 Davey–Stewartson I equation 307
0
2
4
6
0
2
4
0
4
8
12
16
Y
Z
-4
-2
-6
-4
-2
Fig. 9.3. Lumps of the solution (9.137) after interaction [439]
q(x, y, t) is the dimensionless envelope of the wave packet and φ(x, y, t)is
the dimensionless amplitude of the mean fluid flow. The initial-value problem
for DS I was addressed by Fokas and Ablowitz [156, 159]. They formulated
the RH problem for the eigenfunctions of the spectral problem but localized
solutions were not been found. In a somewhat more general (in fact, noninte-
grable) form the DS I type equation arises in nonlinear optics when studying
propagation of a single quasimonochromatic optical pulse in a nonresonant
quadratic medium [2].
A breakthrough in finding true solitons in 2+1 dimensions was caused
by the remarkable discovery by Boiti et al. [62, 63, 365]. They demonstrated
by means of the B¨acklund gauge transformation that exponentially localized
solitons of the DS I equation exist if specific boundary conditions are properly
taken into account. This new situation can be explained in physical language.
Indeed, in 1 +1 dimensions, where solitons are the result of the balance between
counter-acting nonlinearity and dispersion, both of these effects are of the
same order of magnitude and are able to compensate each other. In contrast,
in 2+1 dimensions dispersion is, as a rule, much strong er than nonlinearity;
hence, additional sources are needed to stop dispersive broadening. Just the
boundaries serve as these sources.
There are two versions of the IST formalism to find solitons of the DS I
equation. Fokas and Santini [162] used the unit normalization of analytic
eigenfunctions of the spectral problem and modified the second (evolutionary)
Lax equation to incorporate nontrivial boundary con d iti ons, while Boiti et al.
[67, 68] normalized eigenfunctions by the boundary conditions, retaining the
second Lax equation to be explicitly integrable. We will follow in this section
the approach of Fokas and Santini as it is technically simpler, though the
method by Boiti et al. seems perhaps more natural from the viewpoint of the
308 9 Dressing via nonlocal Riemann–Hilbert problem
IST ideology. Note that the so-called dromion solutions of the DS I equation
were derived by the
¯
∂ formalism in the book by Konopelchenko [241].
9.3.1 Spectral problem and analytic eigenfunctions
The DS I equation (9.138) arises as the compatibility condition of the system
of linear equations (the Lax pair)
ψ
x
+ σ
3
ψ
y
+ Qψ =0,Q=
0 q
ǫ¯q 0
, (9.139)
iψ
t
+ σ
3
ψ
yy
+ Qψ
y
+ Aψ =0. (9.140)
Here ψ(x, y, t)isa2×2 matrix function and the 2 ×2matrixA will be specified
later. Because the spectral problem (9.139) is hyperbolic, it is reasonable to
use the coordinates ξ = x + y and η = x − y. In new coordinates the seco nd
equation in (9.138) takes the form
φ
ξη
=
ǫ
2
(∂
ξ
+ ∂
η
)|q|
2
. (9.141)
Integrating (9.141) in turn in ξ and η,weobtain
φ
ξ
= −U
1
+
ǫ
2
|q|
2
,U
1
(ξ,η)=−
ǫ
2
η
−∞
dη
′
|q|
2
ξ
+ u
1
(ξ,t), (9.142)
φ
η
= −U
2
+
ǫ
2
|q|
2
,U
2
(ξ,η)=−
ǫ
2
ξ
−∞
dξ
′
|q|
2
η
+ u
2
(η, t).
Here the real functions u
1
(ξ,t)andu
2
(η, t) represent the boundary values of
U
1
and U
2
:
u
1
(ξ,t) = lim
η→−∞
U
1
(ξ,η, t),u
2
(η, t) = lim
ξ→−∞
U
2
(ξ,η, t). (9.143)
Then the DS I equation is written as
iq
t
+ q
ξξ
+ q
ηη
+(U
1
+ U
2
)q =0. (9.144)
Hence, we can consider the DS I equation as the integrodifferential equation
for complex function q(x, y, t) with boundary conditions (9.143) and definite
dependence (9.142) of U
1
and U
2
on q. Just the real functions U
1
and U
2
enter
the matrix A in the evolutionary part (9.140) of the Lax pair:
A =
U
2
−q
η
ǫ¯q −U
1
. (9.145)
We assume that q(ξ, η, 0), u
1
(η, t), and u
2
(ξ,t) decay for large ξ and η.Our
aim is to solve the initial boundary value problem for the DS I equation.
