Дипломная работа - Проектирование автоматизированной системы управления процессом измельчения сульфидной руды

Подождите немного. Документ загружается.

прохождения материала, сокращая, таким образом, продолжительность

измельчения и уменьшая переизмельчение материала, что способствует

повышению содержания крупного класса в материале, находящемся в

мельнице, и увеличению её производительности. Добавка готового продукта

к комбинированной загрузке мельницы, вследствии несовершенства

классификации, хотя и увеличивает скорость прохождения материала через

мельницу, в целом отрицательно влияет на работу мельницы. Проходя

повторно через мельницу, готовый продукт переизмельчается, поглощая

бесполезно энергию и затрудняя дальнейшие операции его обогащения.

Повышение средней крупности руды, поступающей в мельницу, или

увеличение твёрдости приводит к росту циркулирующей нагрузки, что при

неизменной величине исходного питания мельницы рудой приводит к её

переполнению. В случае понижения средней крупности и твердости

циркулирующая нагрузка снизится и при неизменном питании мельницы

рудой резерв производительности её не будет использован.

Основным показателем процесса классификации принято считать

средний диаметр твёрдых частиц, выделяемых в слив. Этот показатель

зависит от плотности пульпы в сливе; чем больше плотность слива, тем

больше количество крупных частиц уходит вместе со сливом, т.е. возрастает

средний диаметр твёрдых частиц.

Работа классификатора регулируется количеством подаваемой в

классификатор воды, в зависимости от чего меняется плотность пульпы на

сливе классификатора. Любое увеличение эффективности классификации

даёт экономию в расходе энергии на измельчение благодаря уменьшению

количества переизмельчаемого материала и позволяет использовать большую

часть энергии, необходимой для вращения барабана мельницы, для

измельчения некондиционных крупных зерен. Следует учитывать, что

изменение количества песков приводит к дополнительному переходному

процессу, вызванному изменением плотности слива в зависимости от

количества и гранулометрического состава поступающей в классификатор

пульпы.

Рассмотрим переходной процесс шаровой мельницы, происходящий

при подаче воды в классификатор, в соответствии с рисунком 1.4. [3]

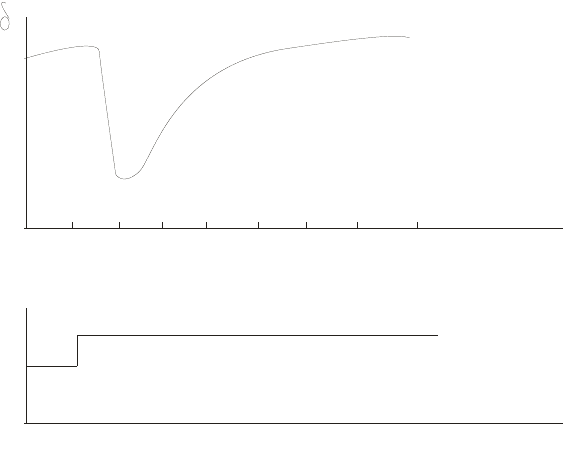
15 30 45 60 75 90 1 50 120 T, мин

T, мин

1400

1600

1800

Gв

где Gв – количество подаваемой в классификатор воды;

 - плотность пульпы.

Рисунок 1.4 – Переходной процесс по каналу: количество подаваемой в

классификатор воды – плотность пульпы.

На рисунке видно, что измельчительный агрегат, работающий в

замкнутом цикле с классификатором, имеет сравнительно сложную

передаточную функцию, которую можно получить путём структурных

преобразований замкнутой схемы измельчительного цикла.

Характер кривой изменения плотности можно объяснить следующим

образом: при увеличении подачи воды происходит кратковременное

снижение плотности пульпы вследствие её разжижения. В это же время

начинается процесс увеличения циркуляционной нагрузки и медленное

увеличение плотности. Переходной процесс длится более часа.

Колебания плотности слива классификатора в значительной мере

сказываются на изменении величины циркулирующей нагрузки

классификатора. Экспериментально установлено, что изменение плотности

слива классификатора на 1% вызывает изменение количества

циркулирующих песков до 30%. Становится ясным, какое важное значение

приобретает вопрос автоматического поддержания на заданном уровне

величины плотности слива классификатора.

1.3 Статистическое моделирование процесса измельчения

Эффективное управление процессом измельчения с использованием

вычислительной техники автоматизированных систем требует знания

математической модели этого процесса, а наличие большого числа

возмущающих воздействий на него позволяет применять лишь

статистическое моделирование. [4]

Математическое описание технологических объектов автоматизации

принципиально возможно детерминистическим и статистическим способами.

При детерминистическом способе математическая модель составляется на

основании имеющейся теории процесса, т.е. точного знания физико-

химических, энергетических и эксплуатационных свойств объекта. Однако

получение этим способом модели, которая связывала бы все управляющие и

возмущающие воздействия и давала количественную оценку влияния

отдельных параметров процесса на его результат, чрезвычайно

затруднительно.

Другой метод – статический - позволяет выявить закономерность

воздействия одних параметров процесса на другие на основании большого

статического материала, собранного в процессе длительной промышленной

эксплуатации агрегата (пассивный эксперимент), либо благодаря специально

спланированному эксперименту, позволяющему при минимальном

количестве воздействий на агрегат выяснить интересующие закономерности

(активный эксперимент).

Экспериментальное исследование сложных объектов, не позволяющих

осуществлять многократные воздействия и требующих больших

материальных затрат на проведение опытов, обусловили разработку методов,

которые позволяли бы не только обрабатывать экспериментальные данные,

но и наилучшим образом организовывать эксперимент. Математический

аппарат, используемый при такой организации эксперимента, базируется на

композиции методов математической статистики и методов решения

экстремальных задач.

В настоящее время можно выделить два основных направления в

математической теории планирования экспериментов: планирование

экстремальных экспериментов и планирование экспериментов по выяснению

механизма явлений или получению математического описания процесса.

Экстремальные эксперименты можно планировать, зная переменные

факторы, наиболее сильно влияющие на процесс. При этом прежде

необходимо провести эксперименты по выяснению взаимосвязи факторов с

параметрами оптимизации.

Так как результаты наблюдений - величина случайная, а процессы

стационарные, то связь средних значений исследуемых величин с

контролируемыми переменными может быть описана некоторой функцией

 

















(1.3)

где E(Y/X) – среднее значение исследуемой величины Y при значениях

контролируемых переменных X, определяемых координатами вектора

η(Х) - функция, зависящая от неизвестных параметров θ1, θ2, …, θm,

для определения которых необходимо проведение исследований

лабораторной модели измельчительного агрегата.

Факторное планирование применяется на первых этапах изучения

сложных технологических процессов с большим числом независимых

переменных с целью выделения наиболее существенных факторов.

Исследования, направленные на отыскание оптимальных условий протекания

процесса, могут потерять всякий смысл, если некоторые из переменных,

существенно влияющие на результаты процесса, не будут включены в

программу исследований. [5]

Для выявления существенных параметров, влияющие на оптимальную

загрузку мельницы, в исследуемую модель включим четыре возможных

переменных фактора: Х1 – количество воды, загружаемой в мельницу

(литров); Х2 – количество загружаемого материала (кг); Х3 –

гранулометрический состав измельчаемого материала (мм); Х4 – масса

измельчающей среды (кг). В качестве параметра оптимизации примем Y –

средний диаметр измельчённого материала (мм).

Опыты для получения статических характеристик проводят в

следующем порядке. В мельницу, загруженную измельчающей средой

массой Х4 (шарами), поступает сырьё крупностью Х3 и массой Х2, и вода

объёмом Х1. Материал измельчается и постоянно выдаётся из мельницы.

Через определённые промежутки времени, в зависимости от смены факторов,

берутся пробы измельчённого материала. После предварительного

обезвоживания проба помещается в сушильный шкаф, где подвергается

сушке. Затем измельчённый материал рассеивается на классы на стандартных

ситах, взвешивается на аналитических весах и определяется средний диаметр

измельчённого материала Y.

Для определения статистических характеристик объектов управления в

процессе их нормальной эксплуатации, то есть выявления наиболее

значимых факторов цикла измельчения из четырёх выбранных применим

корреляционный и регрессионный анализ. Экспериментальные данные,

полученные в результате специального опробования технологического

процесса обработаем с помощью электронного табличного процессора

«EXCEL». Множественный корреляционно-регрессионный анализ

ориентирован на средства дополнительного пакета «Анализ данных». [6]

1.4 Корреляционно-регрессионный анализ

В электронную таблицу «EXCEL» внесём данные 13 испытаний.

Таблица 1.1 – Данные опытов для получения статических

характеристик.

X1 X2 X3 X4 Y

7 26 6 60 1,784

1 29 15 52 1,689

11 56 8 20 2,37

11 31 8 47 1,99

7 52 6 33 2,179

11 55 9 22 2,482

3 71 17 6 2,334

1 31 21 44 1,648

2 54 18 22 2,116

21 47 4 26 2,634

1 40 23 34 1,904

11 66 9 12 2,575

10 68 8 12 2,486

С помощью инструмента «Корреляция» получим корреляционную

матрицу парных коэффициентов.

Таблица 1.2 - Матрица парных коэффициентов.

 X1 X2 X3 X4 Y

X1 1 " " " "

X2 0,228579 1 " " "

X3 -0,82641 -0,12745 1 " "

X4 -0,24545 -0,97295 0,019037 1 "

Y 0,73054 0,816323 -0,52514 -0,8214 1

На основе полученной матрицы проведём корреляционный анализ:

 среди независимых переменных имеется пара Х1, Х3 с сильной

обратной связью (-0,82641). Следовательно, одновременное участие Х1

и Х3 нецелесообразно;

 имеется ещё одна пара независимых переменных Х2, Х4 с весьма

сильной обратной связью (-0,97295). Следовательно, одновременное

участие Х2 и Х4 ещё более нецелесообразно;

 независимая переменная Х3 имеет с зависимой Y менее выраженную

связь, наименьшую по модулю из всех независимых. Поэтому Х3 –

явный кандидат на исключение из четырёх факторной модели;

Поиск наилучшего уравнения будем выполнять методом исключения,

планируя получить и исследовать уравнения:

 с факторами Х1, Х2, Х3, Х4;

 с факторами Х1, Х2, Х3;

 с факторами Х1, Х2.

Расчёт параметров четырёхфакторного уравнения с полным набором

независимых переменных показывает значимость в целом уравнения, но, как

показано в таблице 1.3, t – статистика выявляет незначимость отдельных

факторов, которая у Х4 ниже всех.

Таблица 1.3 – Результат расчёта параметров четырёхфакторного

уравнения.

 Коэффициенты Стандартная ошибка t-статистика P-Значение

Y-

пересечение 0,750427807 1,601672622 0,468527586 0,651908528

X1 0,042518127 0,017221921 2,468837647 0,038780666

X2 0,018328444 0,016430838 1,115490484 0,297024257

X3 0,009947225 0,017728682 0,561080885 0,590107988

X4 0,003398965 0,016188693 0,209959202 0,838948039

Х4 – кандидат на исключение в следующем шаге.

Расчёт параметров трёхфакторного уравнения с набором независимых

переменных Х1, Х2, Х3 показывает значимость в целом уравнения, но, как

показано в таблице 1.4, t – статистика выявляет незначимость отдельных

факторов, которая у Х3 ниже всех.

Таблица 1.4 – Результат расчёта параметров трёхфакторного

уравнения.

 Коэффициенты Стандартная ошибка t-статистика P-Значение

Y-

пересечение 1,086146901 0,087879521 12,35949959 5,98569E-07

X1 0,039051047 0,004622977 8,447164912 1,42971E-05

X2 0,014885681 0,000992116 15,00397176 1,12551E-07

X3 0,006346726 0,004252512 1,492465012 0,169776471

Х3 – кандидат на исключение в следующем шаге.

Расчёт параметров двухфакторного уравнения с набором независимых

переменных Х1, Х2 показывает, что они являются наиболее значимыми

факторами , как показано в таблице 1.5, t – статистика выявляет значимость

отдельных факторов.

Таблица 1.5 – Результат расчёта параметров двухфакторного

уравнения.



Коэффициент

ы Стандартная ошибка t-статистика P-Значение

Y-

пересечение 1,194870502 0,052081407 22,94236211 5,58795E-10

X1 0,033354093 0,00276336 12,07012222 2,76559E-07

X2 0,015051656 0,001044618 14,40876799 5,14241E-08

Наилучшее уравнение для вычисления зависимой переменной Y:

015,00333,0195,1 XXY 

(1.4)

На основании корреляционно-регрессионного анализа полученных

данных можно сделать вывод о том, что основными возмущающими

воздействиями влияющими на загрузку мельницы, являются количество

воды и количество материала загружаемые в мельницу.

2 СОЗДАНИЕ СИСТЕМЫ АВТОМАТИЗАЦИИ ПРОЦЕССА

ИЗМЕЛЬЧЕНИЯ

2.1 Назначение и цель создания системы автоматизации

Обогатительные комплексы занимают промежуточное положение в

цепи производственных процессов добычи и использования полезных

ископаемых. На вход обогатительных фабрик поступает сырьё,

вещественный состав которого отличается значительным непостоянством во

времени, а на выходе должен быть получен кондиционный продукт,

удовлетворяющий потребителя по своим качественным показателям.

Решение этой задачи невозможно без автоматизации контроля процессов

обогащения, регулирования режимов работы машин и механизмов.

Одной из важнейших задач автоматизированного управления

производственным процессом является установление и поддержание

оптимального технологического режима, то есть такого комплекса значений

основных технологических параметров, которые обеспечивают наиболее

высокие экономические показатели процесса. Успешное выполнение этой

задачи при сложности процессов обогащения невозможно без применения

средств автоматики и вычислительной техники.

Автоматизация обогатительных процессов – высшая ступень

получения и использования информации, обеспечивающая достижение

поставленных целевых функций, а также облегчающая труд

обслуживающего персонала, расширяющая их возможную зону

обслуживания и, в итоге, повышающая производительность труда.

Основа систем автоматизации – автоматические системы

регулирования (АСР) отдельными параметрами. На их основе создаются

автоматизированные системы управления технологическими процессами

(АСУТП).

Автоматизированные системы управления решают следующие

основные задачи:

 измерение параметров процесса и контроль состояния оборудования;

 централизованный сбор и первичная обработка информации;

 мониторинг технологических показателей;

 расчёт технико-экономических показателей.

Основной целью создания автоматизированной системы управления

является повышение эффективности функционирования действующей

обогатительной фабрики за счет следующих факторов:

 оптимизации управления технологическими процессами на основе

качественных измерений, физико-химических и математических

моделей технологических процессов;

 модернизации и замены физически изношенных средств и систем

автоматизации;

 интеграции разрозненных систем и контуров управления

технологическими процессами.

Особо важное значение в интеграции систем приобретает

централизованное автоматизированное управление на обогатительных

фабриках вследствие наличия большого числа технологических потоков и

механизмов. Централизованное управление одним контуром измельчения

реализуется в виде операторской панели, на которой сведены управление и

контроль за работой основных механизмов технологической цепи.

Переменные качества исходной руды по крупности, влажности,

твёрдости и другим факторам сильно осложняют задачу автоматической

оптимизации режима измельчения. Процесс измельчения физически тесно

связан с процессом классификации. Эти два процесса находятся, как правило,

в замкнутом цикле. Поэтому технологические параметры, характеризующие

каждый процесс в отдельности, находятся между собой в динамической

связи. Отсюда видно, что решать вопрос автоматизации измельчения и

классификации отдельно друг от друга нельзя; в данном случае необходимо

рассматривать как один объект «мельница-классификатор». Конечным

критерием, определяющим работу измельчительно-классифицирующего

агрегата, является максимальная производительность при заданных классах

крупности в готовом продукте. Для решения данной задачи применяются

автоматические системы регулирования.

Основная цель классических автоматических систем регулирования –

стабилизация y(t) на заданном уровне yо путём изменения его входной

величины x(t) в условиях, когда на входе объекта действует возмущение z(t),

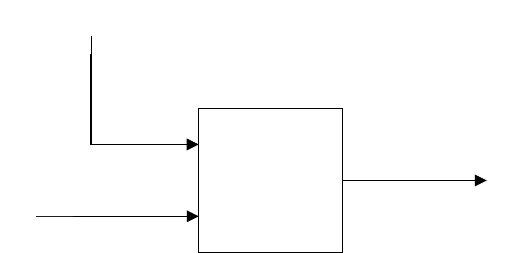
в соответствии с рисунком 2.1 [7]

Рисунок 2.1 – Структурная схема объекта автоматизации.

Величины x(t) и y(t), с одной стороны, и y(t) с другой стороны, связаны

как причина и следствие; количественно такие причинно-следственные связи

Объект

y(t)

x(t)

z(t)

оценивают математическими закономерностями, которые для статического

режима объекта имеют вид функциональной зависимости y = f (x, z). [8]

В автоматических системах регулирования без обратной связи (по

возмущению) регулятор управляет входной величиной x(t) объекта

(процесса) без измерения выходной величины y(t), но с измерением

возмущения z(t), сигнал которого подаётся от измерительной системы на

вход регулятора.

В автоматических системах регулирования с обратной связью

регулятор управляет входной величиной x(t) объекта (процесса) на основе

измерения только его выходной величины y(t); возмущения z1, z2,.. не

измеряются. Выходная величина объекта y через измерительную систему

передаётся на вход регулятора, в котором определяется отклонение от

задания:

   

ytyt 

(2.1)

Затем формируется алгоритм управляющего воздействия на входе

объекта

 

 fx

. В простых типовых пропорциональных регуляторах (П -

регуляторах) воздействие регулятора пропорционально отклонению



, т.е.

   

tktx



(2.2)

где

- статический коэффициент передачи.

В более сложных типовых пропорционально-интегрально-

дифференциальных регуляторах применяется ПИД – алгоритм

     

 









Дp

иpp

tdTk

dttTktkxt

(2.3)

где

- статический коэффициент передачи;

- постоянная времени интегрирования;

- постоянная времени дифференцирования.

Постоянные времени интегрирования и времени дифференцирования

выбирают в зависимости от статических и динамических характеристик

объекта(т.е. от вида математического уравнения, связывающего выход y и

вход x объекта). [9]

С состав системы автоматизации процесса измельчения входят две

подсистемы: система управления циклом измельчения и система

стабилизации параметров измельчения.

2.2 Cистема управления циклом измельчения

Cистема управления циклом измельчения предназначена для пуска в

работу, согласно заданному алгоритму, агрегатов входящих в состав цикла

измельчения, останова, сигнализации состояния, контроля за