Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

302 6 Electromagnetic Properties

Fig. 6.13 Block diagram of

uniform-precession spin

energy transfer to the lattice

in a magnetic garnet. Note

effect of the c-sublattice

rare-earth ions and the

expected inﬂuence the Fe

spin canting [47]. Figure

reprinted from [47] with

permission.

 2000 by the

American Institute of Physics

where  is a factor that is proportional to the concentration of RE ions and the

energy of their exchange coupling to the iron sublattices. The RE relaxation rate

can be approximated as 

1

 C

eff

exp .=kT/,where is the splitting of the

lowest excited state of the rare-earth multiplet as described in Sect. 6.1.

To evaluate the parameter , we consider the molecular ﬁeld surrounding iso-

lated paramagnetic ions of the rare-earth series. From the discussion in Chap. 4,the

exchange ﬁeld can be expressed as

D N

C N

; (6.70)

where N

are molecular-ﬁeld coefﬁcients expressed in mol cm

3

and M

is the

undiluted magnetic moment per mole of the i sublattice ([52, 53]ofChap.4). The

labeling of sublattices is according to crystallographic sites, with d for tetrahedral,

a for octahedral, and c for the dodecahedral site of rare-earth ions. Table 6.4 lists

the values of N

for the RE ions of interest. Note that the intra-sublattice coefﬁ-

cient N

is negligible, which allows for the c moments to be treated as coupled

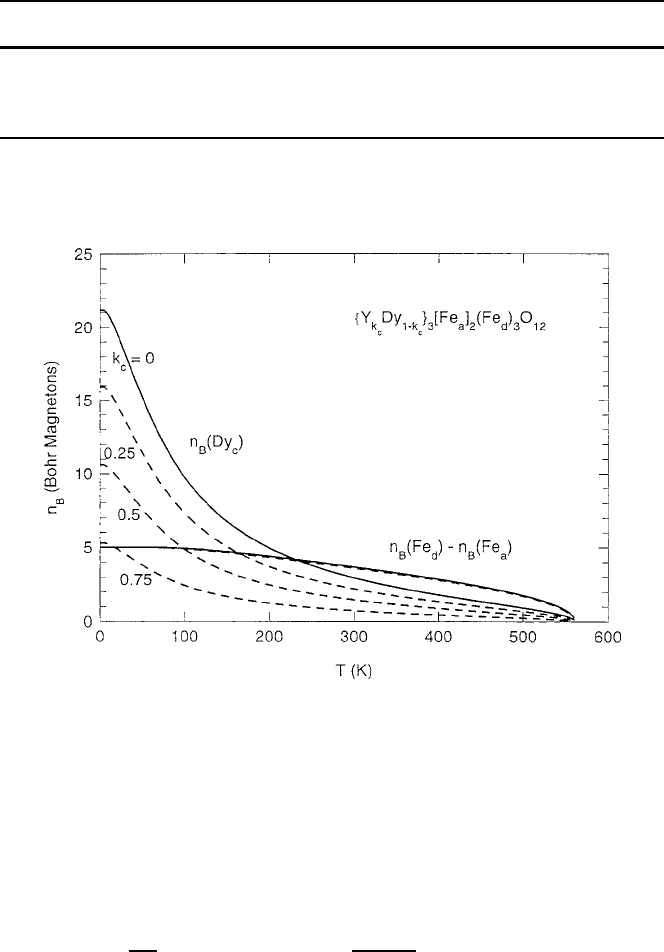
only to the iron ions. Figure 6.14 illustrates how the c sublattice moment n

(ex-

pressed in Bohr magnetons of Dy

) decreases sharply with increasing temperature

and scales directly with the dilution fraction k

, while having virtually no effect on

the net moment of the opposing iron sublattices. In this sense, the c sublattice com-

prises relaxation centers with the spin–lattice interaction of isolated paramagnets.

The effectiveness of RE ions in transferring microwave energy of spin waves from

the Fe

spin systems to the lattice depends directly on the exchange energy per

mole, E

D M

To compute E

as a function of temperature, M

.T / and H

.T / must be

extracted from the complete molecular ﬁeld solution involving the temperature

variations of Brillouin functions for the three-sublattice magnetic garnet. From these

6.2 Gyromagnetic Resonance and Relaxation 303

Table 6.4 Rare-earth ion parameters

(RE) Bohr

RE Ion magnetons



mol cm

3





mol cm

3



eff



1

10





7.07 6.0 4:0 8.45 50

6.23 4.0 2:1 24.4 100

5.54 2.2 0:2 5.26 125

1.70 8.0 4:0 3.47 175

Spectral measurements in paramagnets indicate that   500 KforYb

. Because this value

is in the order of the Debye temperature, the Orbach process is not fully applicable and could be

replaced by a Raman process [4]

Fig. 6.14 Calculated thermomagnetic curves of



1x



with the c sublattice sepa-

rated from the net of the opposing d and a sublattices. Magnetic moments are expressed in n

(Bohr magnetons per formula unit) [47]. Figure reprinted from [47] with permission.

 2000 by

the American Institute of Physics

concepts, we construct the following models for the relaxation rate and intrinsic

linewidth as a function of temperature and RE ion concentration [47]:



1

D AT

C C

eff

exp .=kT/ ; (6.71)

H

D 

1



„!



C

.1  k



.T /

.0/



eff

exp .=kT/



; (6.72)

where A and C

eff

are proportionality constants in appropriate units, and the exponent

n  1. For ﬁrst approximations, 

1.

304 6 Electromagnetic Properties

Fig. 6.15 Comparison of theory with selected data of X-band FMR half-linewidth as a function of

temperature for



0:99

0:01



and

0:99

0:01

[47]. Data are from Seiden [41].

Figure reprinted from [47] with permission.

 2000 by the American Institute of Physics

Figure6.15 presents an example of the ﬁt of theory to Seiden’s data scaled to 1%

ionic concentration of Dy

,Ho

in YIG, i.e., .Y

0:99

0:01

, follow-

ing his original format [41]. In Table 6.4, the values of C

eff

and  and for a signal

frequency of 9.2 GHz as determined by adjustment of computed curves to data are

listed for each case. The magnitude of the D splittings are consistent with those ex-

pected from the values of the particular RE ion moment [48] and the corresponding

exchange ﬁelds that are determined by the N

and N

coefﬁcients ([53] of Chap. 4)

listed in Table 6.4. Relaxation rate vs. temperature data from the studies of Spencer

and LeCraw on a specimen of high purity single-crystal YIG [49] were analyzed by

computation employing (6.72) and plotted as intrinsic H in Fig. 6.16. Because the

concentration of RE ions is so small, the major temperature dependence is from the

iron sublattices modeled semiempirically with A D 236 sK

2:5

and n D 2:5.Dy

was selected as the fast-relaxing ion, and the concentration (1  k

)  4  10

7

necessary to produce the slight peak near T D 40 K.

Relaxation of the iron spins in garnets is closer to a T

1

direct process, with

little evidence of a T

9

Raman contribution. As T increases, two factors in (6.13)

cause H

to decrease: „!=kT and E

.T /. It should also be pointed out that the

Orbach function [6, 7] applies to a paramagnetic system with no exchange ﬁeld,

and is the low-temperature approximation to 

1

D C

eff

Œexp .=kT /  1

1

, from

(6.72). If this more rigorous expression were used, the computed H

would not

decrease as quickly above the temperature of the peak. However, if the Orbach for-

malism included E

as an exchange energy splitting in the two-phonon process, the

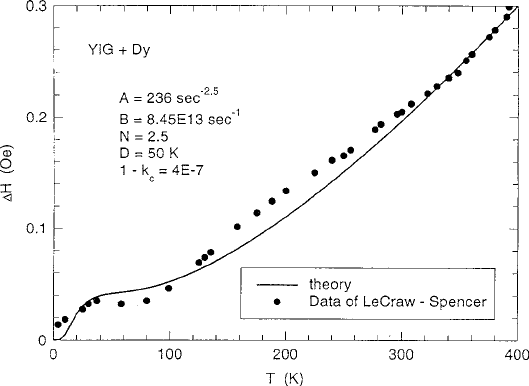
6.2 Gyromagnetic Resonance and Relaxation 305

Fig. 6.16 Comparison of theory with X-band FMR half-linewidth data as a function of tempera-

ture for high-purity YIG specimen [47]. Data are from LeCraw and Spencer [49]. Figure reprinted

from [47] with permission.

 2000 by the American Institute of Physics

coefﬁcient C

eff

would then be subjected to the strong temperature dependence of

[50]. 

1

would therefore decrease more sharply at higher T , thereby offsetting

the error in H

introduced by the low-temperature approximation.

Other ions besides rare earths that satisfy the =ı  1 condition can provide

fast relaxation paths to the lattice bath. In the iron sites of both garnets and spinels,

and Fe

in octahedral sites are common because of their spin–orbit dou-

blet stabilization in an exchange ﬁeld. Less frequent, but nonetheless signiﬁcant

in select situations, Mn

in octahedral sites [51],showninFig.6.17,aswellas

in tetrahedral sites can also produce enhanced linewidths at low temperature.

Table 5.9 summarizes qualitatively the effects expected for the 3d

series in high-

spin states. An instructive example of rapid relaxation from Fe

)ina

low-spin state (S D 1=2) was reported by Kipling et al. [52] for the host compound

.CN/

Another consideration that will be examined in Chap. 7 in connection with

magneto-optical Faraday rotation is the inﬂuence of Bi

and Pb

on the iron sub-

lattices. Because these ions have a wide ranging 6s outer orbital that can hybridize

with 2p orbitals of O

2

and the half-ﬁlled 3d orbitals of Fe

, all of the relevant

overlap integrals could be affected. Evidence of these interactions was found in

the Curie temperature of BiIG that exceeded that of pure YIG by 38 K [53]. Later

Mossbauer analysis revealed that the presence of Bi

correlated with a reduced

negative exchange interaction in the tetrahedral sublattice, which suggests a possible

direct ferromagnetic contribution between d-site Fe

ions [54]. Further indica-

tion of inﬂuence on the Fe

spin system appears in the spin–lattice relaxation rate

through hybridization of the 6sp excited state with the 6s

excited state. With a very

306 6 Electromagnetic Properties

Fig. 6.17 15-GHz FMR linewidth of single crystal Y

4:99

0:01

at cryogenic temperatures,

indicating signiﬁcant spin–lattice coupling due to the magnetoelastic property of Mn





the octahedral a sublattice. Data are from Georgy et al. [51]

large spin–orbit coupling constant (17;000 cm

1

) similar to RE ions, the forma-

tion of hybrid ground states can cause strong microwave damping effects [55].

6.2.6 The Exchange Isolation Effect

Throughout Chaps. 5 and 6 the ratio of spin–orbit coupling to crystal-ﬁeld energy

=ı has recurs wherever orbit–lattice interactions are discussed. Its deﬁnitive role in

determining the anisotropic g factors of Ti alum and other transition-metal ions in

paramagnetic systems, its importance in selecting the spontaneous ligand distortions

(Jahn–Teller vs. spin–orbit), and its critical contribution to the mechanism of spin–

lattice relaxation of electromagnetic spin excitations have all been reviewed. A large

value of =ı usually means strong magnetoelasticity [56]. Perhaps the best exam-

ples are the 4f

rare-earth ions with >10

1

and ı<10

1

. By contrast,

the 3d

series features =ı < 1, but with notable exceptions, such as Co

in an

octahedral site.

In certain situations, the overall lattice magnetoelastic effects from local dis-

tortions are erased due to magnetic dilution. This phenomenon was labeled as an

exchange isolation effect and was ﬁrst noted as an absence in sign reversal of the

anisotropy constant K

with increasing Co

substitutions in Li spinel ferrite when

substitutions are made for Fe

in octahedral sites [57,58]. To preserve charge

neutrality, additional Li

is added to tetrahedral sites. The net result is that small

concentrations of Co

ions in octahedral sites can be surrounded by nonmagnetic

6.3 Exchange-Coupled Modes (Spin Waves) 307

and Ti

ions in neighboring sites of either iron sublattices, thereby removing

much of the H

and essentially rendering the Co

ions paramagnetic. Further ev-

idence that Co

was removed from the collective spin system but retained its local

site spin–lattice coupling was the absence of related spin wave effects and the in-

crease of FMR line broadening from neighboring dipolar interactions. Local effects

from isolated Co

are also apparent at lower frequencies in NiZn spinels where a

separate higher  dispersion frequency peak occurs for small concentrations, only to

pull the main Fe

peak up to it as the Co

level is raised to the percolation thresh-

old for iron–cobalt magnetic exchange ordering. [59]. In the garnet systems, Llabres

et al. reported a similar isolation effect in a Co

-substituted vanadate iron garnet

system [60] and a later observation appears to have been made with tetrahedral-site

isolating octahedral-site Co

in yttrium iron garnet [61].

6.3 Exchange-Coupled Modes (Spin Waves)

The subject of propagation losses that can result from the generation of traveling

spin waves or magnons acting as indirect funnels for converting microwave energy

into lattice phonons will now be introduced in the context of (1) degenerate spin-

wave modes triggered by lattice inhomogeneities and (2) nonlinear growth of spin

waves amplitudes from high rf signal power. With specimens of ﬁnite dimensions,

the uniform precession line can also be divided into a spectrum of gyromagnetic

standing waves (magnetostatic modes) caused by nonuniformities in internal mag-

netic ﬁelds or variations in the rf ﬁeld amplitudes within the specimen volume.

6.3.1 Uniform Precession Decoherence (Degenerate Spin Waves)

In a system of exchange-coupled spins, decoherence of the uniformly precessing

spins can occur analogously to paramagnetic systems, but through a different mech-

anism. Where individual spins are perturbed thermally by spin–phonon collisions

or as a result of local crystal imperfections, magnetic dilution, or high-intensity

nonuniform H

ﬁelds, the precession can vary spatially. Periodic phase ﬂuctuations

can then propagate in the manner of lattice vibrational modes. Under these condi-

tions, we must take into account the spin-phase variations that are dependent on the

restoring force from magnetic exchange ﬁeld H

rather than the random dipole–

dipole interactions of a paramagnetic system.

Figure6.18 illustrates the contrast between the uniform precession mode and the

spatial variation of M

x;y

as the wave propagates parallel and transverse to the z-axis

of the magnetic ﬁeld. Because of the wave nature of the phase and the similarity to

phonons, these modes are called spin waves or magnons. The erosion of the uniform

precession mode by spin waves is an important concern for microwave propagation

in ferrites at high microwave power levels.

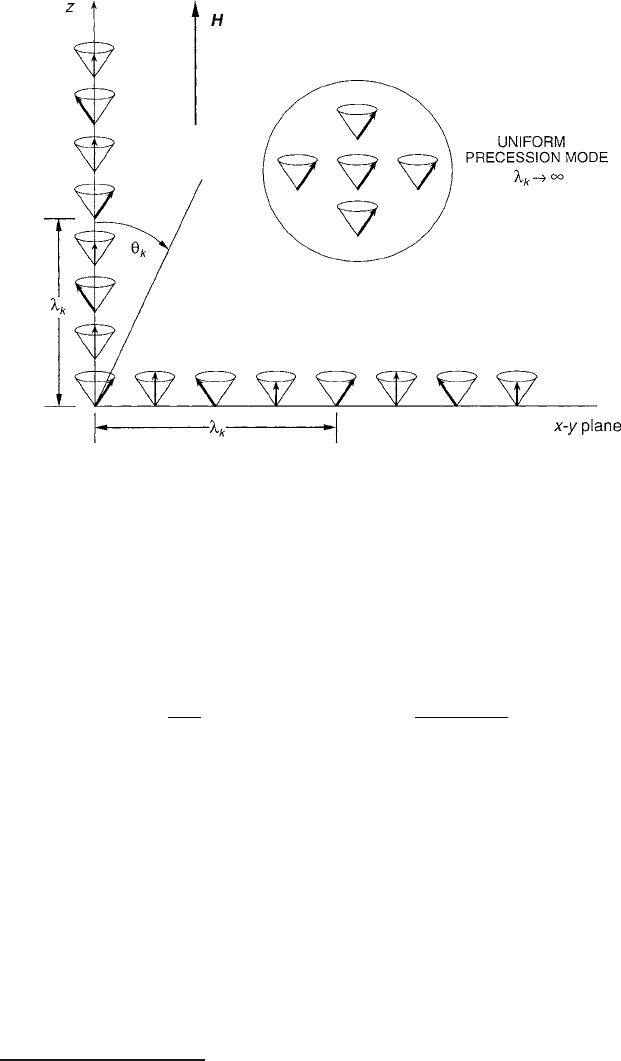
308 6 Electromagnetic Properties

Fig. 6.18 Tutorial diagram contrasting the essential features of gyromagnetic precession in the

form of traveling spin waves of wavelength 

and the static uniform precession with  D1

The physical origin of spin waves resides in the exchange ﬁelds that align the

spin directions. In contrast to dipole–dipole coupling of paramagnets that depends

on the spatial proximity of the spins, the restoring force that gives rise to spin waves

is derived from the local exchange ﬁeld. A rate equation for this effect (without

spin–lattice damping) can be expressed as [62]





D .M  H / C !

M r

; (6.73)

where a is the lattice distance between spins and !

D H

D N

The frequency of a spin wave propagating at an angle 

to the z-axis in an

ellipsoidal specimen of demagnetizing factor N

can be derived by assuming that

the rf magnetization M

x;y

generated by H

in the x–y plane varies according

to the plane-wave function exp Œi .!t–k  r/,togiver

M Dk

M. With this

relation, the component equations in emu can be expressed as



4M



D 4M



C !



 .4M

and



4M



D4M



C !



C .4M

; (6.74)

The derivation of the exchange term in (6.73) can be found in Lax and Button [21]

6.3 Exchange-Coupled Modes (Spin Waves) 309

from which the following components of the rf susceptibility analogous to (6.120)

in Appendix 6A can be extracted:



D 

4

.4M

 !

;



D

x;y

y;x

Di

4

.4M

 !

: (6.75)

For small signals, we can assume that M

 M , and express the resonance fre-

quency for the k spin-wave mode as

D g



C H



; (6.76)

where the magnitude of the wave vector k D 0, !

D H

, the uniform precession

frequency. For k>0, !

represents the precession frequency of a spin wave of

wavelength 2=k determined by the sum of the uniform mode frequency and the

contribution from the exchange ﬁeld.

With the inclusion of magnetocrystalline and shape anisotropy demagnetizing

ﬁelds H

and N

.4M

/, respectively, the frequency of spin waves directed at an

arbitrary angle 

to the z-axis of the applied magnetic ﬁeld H can be expressed in

general terms based on !

in (6.44)as

D 





H  H

 N

4M

C H







H  H

 N

4M

C H

C 4M

sin







: (6.77)

From this relation, the conditions under which the uniform precession and higher

modes are degenerate, i.e., share the same !

, can be determined. The range of

propagation directions from 

D 0 to =2 gives rise to many possible situations

where the waves of different k can couple or scatter without a change in energy

as in a direct two-magnon process. Three-magnon scattering in the manner of the

Raman processes discussed in Sect. 6.1 in relation to spin–phonon interactions are

also possible [63].

By inspection of (6.77), we see that the geometric shape of the specimen and its

magnetocrystalline anisotropy are important in determining the degree of degener-

acy between the various k waves and the k D 0 (uniform precession mode). The

limits to the width of the spin-wave manifold (assuming H

D 0) within which

the degeneracy with the k D 0 mode can exist are illustrated by the 

D 0 and



D =2 curves in Fig. 6.19. As indicated, only an ellipsoidal specimen approx-

imating a thin disk magnetized normal to its axis (N

D N

D 1) can have a

uniform precession that is not degenerate with spin waves. This is because its dis-

persion curve touches only the lower edge (

D 0)ofthemanifoldatk D 0.

A uniform precession frequency within the manifold satisﬁes the degeneracy re-

quirement for the transfer of energy to spin waves.

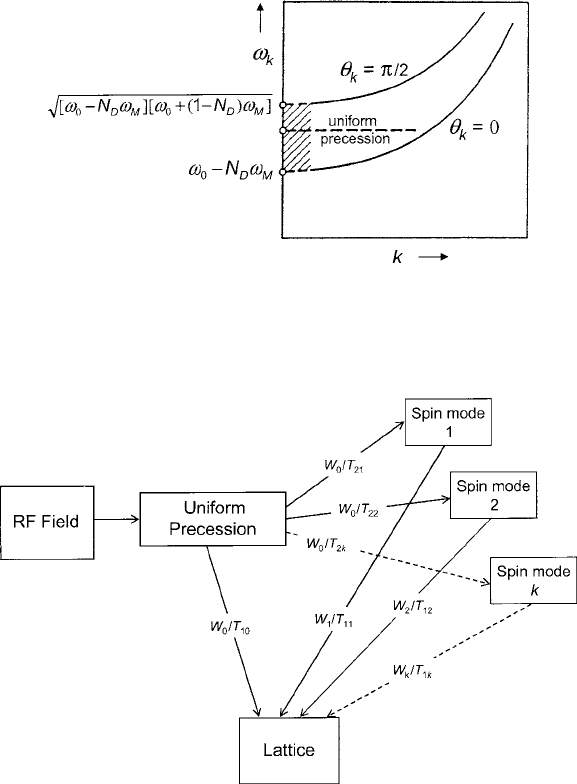
310 6 Electromagnetic Properties

Fig. 6.19 Standard diagram of the spin-wave manifold envelopes within which the uniform

precession mode can exist simultaneously with spin waves. Figure reprinted from [68] with per-

mission.

 1956 by the IEEE

Fig. 6.20 Standard diagram of the distribution of individual spin waves of mode k from the uni-

form precession

k D 0

reservoir. Figure reprinted from R.C. Fletcher, R.C. LeCraw, and E.G.

Spencer, Phys. Rev. 117, 1665 (1960) with permission.

 1960 by the American Physical Society.

http://link.aps.org/doi/10.1103/PhysRev.117.1665

In terms of magnetic susceptibilities, degenerate spin waves can introduce a line

broadening analogous to the dipolar decoherence characterized by the relaxation

time 

. A spin wave of vector k would be assigned a time 

. For the general case,

where a spectrum of k values are possible, the rate 

1

kD0



1

is the sum

of n participating modes ranging from k D 0 (uniform precession) to n. Figure 6.20

6.3 Exchange-Coupled Modes (Spin Waves) 311

diagrams how this occurs. If we assume that 

 

for all modes,

the imaginary

susceptibility of (6.55) is expressed as the paramagnetic case



M



1 C 

.H  !/

C 



; (6.78)

where 

D 

and 

1

D .2

1

C 

1

. Following the model of Schloemann

et al. [64], the absorption component at ! D H can be expressed as



.0/

1 C C



H



1

 1  C



H



; (6.79)

where H

=H  1 and C D 

=

. Note that (6.79) reduces to (6.56)when



D 2

At this point, it should be remarked that the growth of H is not of fundamental

origin, but rather the result of random k>0modes that occur from spatial and

structural inhomogeneities within a particular specimen geometry. Surface irregu-

larities probably also contribute to the linewidth of single crystals [65], although

inhomogeneous broadening due to direct demagnetization has also been proposed

as the cause of H increases in rough-surfaced spheres of polycrystals [66]. The

major cause of spin-waves, however, comes from the development of an instability

in the uniform precession that occurs above an rf power threshold.

6.3.2 Instability Threshold (Classical Approximation)

Although magnetic inhomogeneities can serve as nucleation points for launching

spin waves that broaden the uniform precession resonance, a more dramatic im-

portant effect occurs when H

reaches a threshold value where the amplitude of

the rf magnetization M

x;y

is sufﬁciently great that we can no longer assume that

 M . At this point M

becomes a meaningful variable, and the system enters

a state of accelerated nonlinear spin-wave generation. Since this effect generally

arises as the large-signal regime is approached, its occurrence is of concern in

higher-power applications, such as long-range radar. To appreciate some of the un-

derlying physics of the uniform precession instabilities that are usually attributed

to nonlinear spin-wave generation, we shall introduce three basic classical concepts

(1) the origin of the instability when M

<M, (2) the critical rf ﬁeld H

crit

,and(3)

the relation for the uniform precession resonance peak as H

increases above H

crit

Because spin–orbit–lattice coupling controls these mechanisms, the propagation of a precessing

magnetic moment should not have much inﬂuence on its relaxation rate, and the variation among



values can usually be ignored.