Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

282 6 Electromagnetic Properties

After substitutions for the relaxation rates from (6.23)and(6.24),



 N



D K

eff



 N



p.ıC / 



 N



p./



; (6.26)

where K

eff

D 2K

=.K

C K

/. In the limit where   kT , N

is small com-

pared to N

and N

,and(6.26) can be simpliﬁed to



 N



 K

eff



p.ıC /  N

p./



: (6.27)

The corresponding phonon excitation probabilities are determined by applying

(6.20) (with the continued assumption that   kT )tobe

p./ exp .=kT/ and p.C ı/  exp Œ.ı C / =kT  : (6.28)

Substitution of (6.27)into(6.28) followed by proper manipulation of the foregoing

relations will result in (6.19), but with a temperature dependence of the relaxation

rate different from (6.22):



D K

eff



M C M



p./ K

eff

Œexp .=kT /  1

1

(6.29)

for ı  kT and M  M

.Since  kT ,(6.29) simpliﬁes further to become



 K

eff



M C M



exp .=kT / D C exp .=kT / : (6.30)

This relation represents the Orbach process [5, 6], which applies where  is less

than the Debye energy h

(or k

), typically less than a 0.1 eV. The reason for

this limit is self-evident when one considers that the phonon created by the relax-

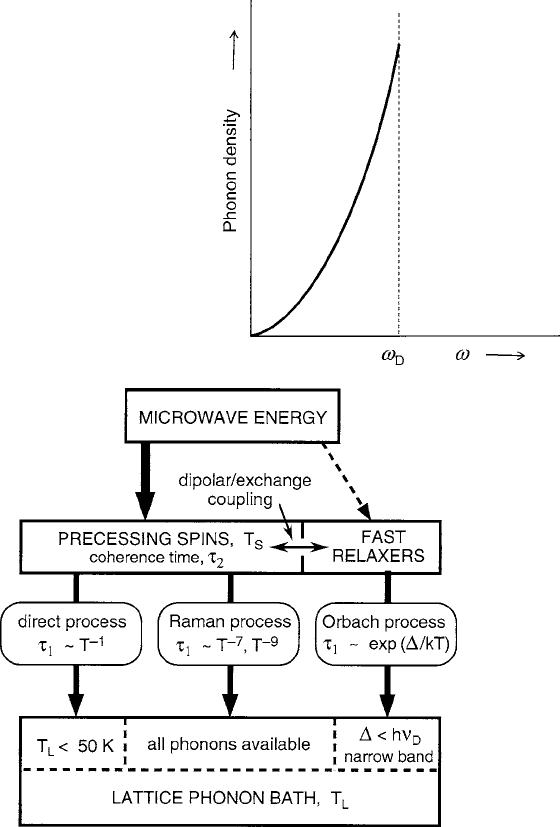
ation from level j3i to level j1i must have a frequency within the allowed phonon

(Debye) spectrum which cuts off at 

, as illustrated in Fig. 6.6. Because   ı

for microwave frequencies, the phonon energy band involved in the Orbach process

is very narrow and centered at h  . Its importance, however, is particularly

signiﬁcant for the heavy rare-earth (4f

) ions owing to their shallow orbital states

that can serve as the third level for a two-phonon process.

In the more general case of two-phonon relaxation,  can be greater than h

level j3i is treated as virtual. While only low-frequency phonons of energy h are

involved in the direct process, in the Raman process the excited spins precessing

in level j2i can relax to level j1i by coupling simultaneously with any two lat-

tice vibration modes provided their energy difference equals h. Compared with

the Orbach process, which we now see as a special case of two-phonon relaxation,

6.1 Magnetic Relaxation 283

Fig. 6.6 Debye model of the

lattice vibration density as a

function of energy. The

function is quadratic up to the

cutoff at the Debye frequency

(or temperature 

which represents the top of

the optical phonon band

Fig. 6.7 Flow chart diagram showing the paths of microwave energy back to the lattice and their

dependence on temperature

Raman processes can occur with any level structure because  is a virtual split-

ting energy. Moreover, they are not restricted to a narrow range of phonon energies

around . At this point, the various relaxation processes can be summarized as pre-

sented in Fig. 6.7.

The quantum mechanical time-dependent formalism of the spin–phonon interac-

tions used to develop the temperature and magnetic ﬁeld relations for the 

of the

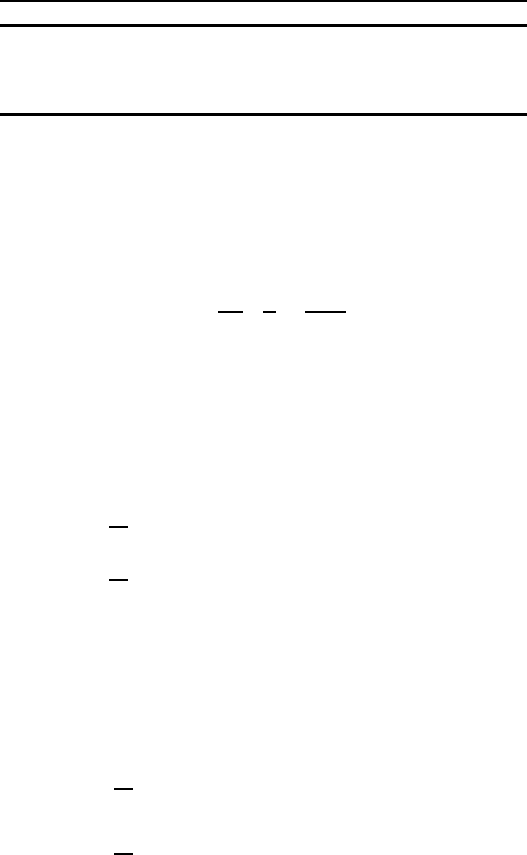
284 6 Electromagnetic Properties

Table 6.1 Relations for spin-lattice relaxation rates 

1

Process Non-Kramers even half-integer S Kramers odd half-integer S

Direct AT C A

Raman BT

C B

Orbach C

eff

exp

=kT

1



1

 C

eff

exp

=kT

eff

exp

=kT

1



1

 C

eff

exp

=kT

Raman process, as well as those for the direct and Orbach processes, are beyond the

scope of this text. However, it is necessary to discuss the results of these analyses,

which are listed in Table 6.1. One important relation that was not included above is

the meaning of the parameter K, which can be expressed as

K D

2



„



„v

; (6.31)

where  is the mass density, v

is the phonon velocity, and A

is a crystal-ﬁeld pa-

rameter in units of potential energy. When this expression is substituted into (6.22),

1=

is found to depend on ı

.Ifpartofı is given by a Zeeman splitting energy

H , a quadratic dependence on H could be expected. The direct process relax-

ation rates are given by



D AT C A

T.non-Kramers/;



D A

T.Kramers/: (6.32)

The distinction between the j1i and j2i states as Kramers (half-integer spin num-

ber) or non-Kramers (integral spin numbers) arises from the subtleties of the

time-conjugate nature of the Kramers doublet, and was explained by [6]. The

proportionality parameters for the corresponding Raman processes are deﬁned by

convention as B, B

,andB

and are stated without derivation [7]:



D BT

.non-Kramers/;



D B

C B

.Kramers/: (6.33)

In comparing the direct, Orbach, and Raman processes, we can ﬁrst dispense with

the Orbach case as peculiar to the low-lying excited state that occurs in only rare-

earth and certain iron-group situations such as 3d

or 3d

. This effect will be seen

to play an important role in the low-temperature ferrimagnetic microwave properties

of rare-earth iron garnets. The more common tradeoffs occur between the direct and

Raman effects as functions of temperature. Therefore, the direct process dominates

6.1 Magnetic Relaxation 285

the low-temperature regime where the Debye spectrum indicated by Figs. 6.6 and

6.7 contains only low-frequency phonons that can match the h of the spin tran-

sition. At higher temperatures, multiple combinations of phonons (real or virtual)

of greater energy become available for the two-phonon Raman process, providing

a more effective means of relaxation than the direct process. Moreover, the Raman

process is not restricted by the narrow-band requirement that the difference in en-

ergy of the two-phonons equal  for the ﬁxed energy of the real excited state needed

for the Orbach process. Illustration of a transition from Raman to direct processes

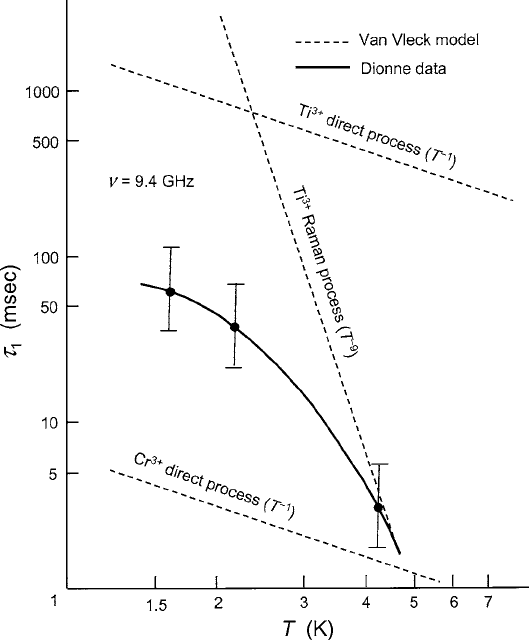
at low temperatures is shown in the data [8] plotted in Fig. 6.8.

Fig. 6.8 Spin–lattice resonance relaxation of Ti

in Rb alum at liquid He temperatures [7]. Note

the transition from Raman to direct mechanisms as T decreases from 4.2 to 1.2 K. Figure reprinted

from [8] with permission.

 1965 by the American Physical Society. http://link.aps.org/doi/

10.1103/PhysRev.139.A1648

286 6 Electromagnetic Properties

6.1.3 Perturbation Theories of Spin–Phonon Interaction

To apply the results of relaxation rate mechanisms listed in Table 6.1,itmustbe

realized that all three of them can be in action simultaneously. What distinguish their

relative effectiveness are the values of the coefﬁcients A, B,andC , and the excited-

state splitting energy  for the Orbach process. The underlying cause of the spin–

lattice coupling is the vibrations of the ligands bonded to the magnetic cation, which

perturb the molecular–orbitalstates and transfer energy through spin–orbit coupling.

To develop a computational formalism, an orbit–lattice Hamiltonian is constructed

from a potential energy relation H

. When combined with the spin–orbit coupling

operator, spin–lattice transition probabilities can be calculated through the standard

off-diagonal matrix elements linking the two states involved in the transition. An

attempt at formulating an orbit–lattice interaction for the direct process was reported

by [9], who deﬁned a crystal-ﬁeld potential by a lattice strain according to H



, averaged over all relevant crystal-ﬁeld orbital states.

For a comprehensive analysis of spin–lattice relaxation, two versions of quan-

tum mechanical perturbation theory can be consulted: ﬁrst, the tour de force by Van

Vleck in which Ti

and Cr

were examined employing six of the vibronic normal

modes of octahedrally coordinated oxygen complexes [10,11], and a later modiﬁca-

tion by Mattuck and Strandberg that was more compatible with the spin Hamiltonian

perturbation approach [12]. The distinction between these two treatments lies in

the order of application of the perturbations. The complete Hamiltonian can be

divided into

H D



lattice

C H

spin



C H

spinlattice

; (6.34)

where the arrangement of Van Vleck is given by

lattice

h







spin

D H

C H

C gm

S  H (6.35)

spinlattice

D L  S C m

L  H C

."V

The subscript n refers to lattice vibration modes, and a

and a



denote phonon cre-

ation and annihilation operators. (The reader is cautioned that the above expressions

have been simpliﬁed.) In the Mattuck–Strandberg version, the L  S C m

L  H

terms are included as part of H

spin

to render the operators more consistent with the

spin-Hamiltonian formalism. For a direct process, the analysis yielded the following

relation for the spin–lattice relaxation rate:







2m

HS C 







.for H D 0/ ; (6.36)

6.2 Gyromagnetic Resonance and Relaxation 287

where S

is the spin anticommutator evaluated between the two spin states. Note

once again the dependence of spin–lattice relaxation on the ratio of spin–orbit cou-

pling to crystal-ﬁeld splitting energies which in this instance is raised to the fourth

power.

In Fig. 6.8, results of 

measurements carried out with a single-crystal of Rb

alum containing a small concentration of Ti

ions are presented for the liquid-

helium temperature range below 4.2 K [8]. The data are compared with calculations

based on the Van Vleck model for the direct process, which is seen to set in as the

temperature is lowered toward 1.2 K. At temperatures in the liquid-nitrogen range

of 77 K, the Raman process is dominant. At 300 K, spin–lattice relaxation times can

be shortened to the order of the spin–spin 

of 10

10

s, depending on the values

of the A, B,andC coefﬁcients. Only for S-state ions such as Fe

or Mn

are the

room-temperature 

levels in the microsecond range.

Other topics of interest are cross-relaxation between dissimilar moments through

dipolar interactions, phonon bottlenecks at low temperatures when low-energy

phonons created by a direct relaxation are slow to disperse their energy to the rest

of the bath, and spin-echo phenomena whereby spin–spin coherence (

relaxation)

can be observed directly by absorption of a sequence of microwave pulses. For a

comprehensive discussion of these subjects and their historical development, the

reader is again directed to [3, 4], and other cited references.

6.2 Gyromagnetic Resonance and Relaxation

As described in the Sect. 6.1, magnetic relaxation is the randomization of magnetic

moments upon the removal of an aligning ﬁeld. In that discussion, energy transfer

by spin–phonon interaction accounted for the longitudinal relaxation of moments

in an ac ﬁeld parallel to the moments, i.e., an amplitude-modulated magnetic ﬁeld.

A more exotic phenomenon that manifests relaxation effects occurs where the ac

ﬁeld is transverse to the aligning magnetic ﬁeld – the condition for gyromagnetic

resonance. Because these ﬁelds are in the radiofrequency and microwave bands, the

symbol used to designate their amplitude is H

In Chap. 1, the classical theory of magnetic resonance was introduced by

Larmor’s theorem of the precessing of a moment vector m about a magnetic

ﬁeld vector H at angular frequency !

(depicted in Fig. 1.16) through the generic

vector relation

D .H  m/; (6.37)

with the Larmor frequency !

and gyromagnetic constant  deﬁned by (1.70),

H D H: (6.38)

and the Larmor spin-ﬂip energy by (1.73),

„!

D gm

HM

D gm

H.for M

D 1/ : (6.39)

288 6 Electromagnetic Properties

Magnetic resonance can occur wherever magnetic moments and ﬁelds satisfy the

orthogonality conditions that lead to (6.37). The material medium can be a gas, liq-

uid, or solid (crystalline and amorphous), and nuclei as well as electrons can provide

the magnetic moment. Although the smaller nuclear magneton (due to the larger

proton mass) produces weaker interactions and reduces the Larmor frequency by a

factor of 1,836 compared with electron-spin resonance, magnetic resonance from

well-shielded nuclei can provide narrow-linewidth signals that are highly frequency

selective. Nuclear magnetic resonance (NMR) has become the basis of the important

medical diagnostic implement, magnetic resonance imaging (MRI), which operates

in the 10–100MHz range in highly stable and uniform magnetic ﬁelds.

Because this text concerns the electronic properties of magnetism, we examine

electron paramagnetic resonance (EPR), ferromagnetic or ferrimagnetic resonance

(FMR), and to a lesser extent antiferromagnetic resonance (AFMR). There are two

main areas of focus (1) EPR as a diagnostic tool for measuring microwave spectra

and deducing the parameters of the spin-Hamiltonian and (2) FMR as a means of

controlling the propagation of electromagnetic waves in rf and microwave systems

through the dependence of the susceptibility on magnetic ﬁeld and magnetization.

Although the phenomenon of magnetic resonance is fundamentally of classical

origins, for EPR a quantum mechanical (QM) analog can be used to depict the res-

onance as an energy transition between two spin states. In effect, it is a magnetic

dipole transition, with the selection rule M

D S

D˙1 (for L  0) satisﬁed.

In Chap.7, magnetic-dipole transitions are discussed in relation to electric-dipole

transitions in the broader context of magnetooptical phenomena.

6.2.1 Paramagnetic Resonance

For the discussion of paramagnetic ions, we can relate a quantum mechanical model

to (6.38) which follows immediately from the realization that the Larmor energy

equates to the splitting of individual magnetic moment degeneracies in a magnetic

ﬁeld. As explained in [13], if damping and decoherence effects are ignored (adia-

batic fast-passage), a simple two-level system at the resonance condition ! D !

can be described in terms of population probabilities p.1=2/ and p.C1=2/ that

vary between 0 and 1 alternatively for the S D1=2 and C1=2 states. This model

is consistent with the angle  between spin direction and z-axis H direction resonat-

ingbetween0and at the effective frequency of the polarized rf drive ﬁeld H

according the relations







D sin



H



Œ1  cos .H

t/;





D cos



H



Œ1 C cos .H

t/: (6.40)

6.2 Gyromagnetic Resonance and Relaxation 289

If in the general case, the angular momentum operator is J , and the stationary state

component J

varies from J to CJ in steps of 1. As a result, the classical mag-

netic energy – mH cos  referred to the polar axis of quantization is accounted

for by gm

averaged over the energy-level ladder and weighted according

to the Boltzmann population fraction exp .gm

=kT/. The comparison of the

two approaches is directly analogous to the reasoning used in the derivation of the

Langevin and Brillouin functions for paramagnetism discussed in Chap. 1. For odd-

electron systems of the 3d

group, the Kramers theorem would apply to S D 5=2,

3/2, as well as 1/2, and the ﬁnal Zeeman splittings can involve as many as ﬁve al-

lowed transitions. In anisotropic crystal ﬁelds, these transitions can be resolved in

the EPR spectrum, either magnetic ﬁeld or frequency scanned in accord with (6.39).

Because EPR is intimately tied to the relaxation processes and will be inﬂuenced

by them in slow-passage situations described in Chap. 1,(6.40) should be accepted

only as a basis for discussion in the comparison of the classical and quantum models.

In the context of the quantum model of resonance damping, the photons supplied by

represent the excitation or pump energy from which the spin–phonon relaxation

follows.

Returning to the two standard examples of EPR vehicles, Ti





and





in octahedral sites discussed in Sect. 5.2, we can examine the crystal-

ﬁeld energy level diagram shown previously in Fig. 5.3 for Ti

and in Fig. 5.14a

for Cr

. The diagrams indicate orbital state energy splittings that were described

in detail in Chap. 2, but now include the Zeeman splittings of the Kramers doublets

that are proportional to the magnetic ﬁeld strength. The diagrams depict the tradi-

tional experimental setup for determining the resonance spectra by sweeping the

dc magnetic ﬁeld at a ﬁxed signal frequency (although the reverse approach has

also become convenient). To relate this approach to the classical Larmor model, we

recognize from (6.39)that„!

D gm

HS

D gm

H ,wherejS

jD1 for

each transition.

In Chap. 5,theTi





ion was discussed as the textbook S D 1=2 case for

perturbation analysis of electronic structure. A sample spectrum of the 12 equiv-

alent, but differently oriented, complexes of Ti

in Rb alum is given in Fig. 6.9

[14]. Each magnetic ion of the 3d

series has its own electronic conﬁguration

and requires an analytical treatment speciﬁc to its peculiarities. In most cases, the

spin-Hamiltonian approximation can be used to solve for the eigenstates and their

energies. A version of (5.14) deﬁned for an axial crystal ﬁeld is expressed as

D g

C g



C H



C D





S.SC 1/



; (6.41)

where g

and g

are the g-factors parallel and perpendicular to the z-axis and D is

an axial symmetry constant that is commonly referred to as the “zero-ﬁeld” split-

ting parameter, shown in Fig. 5.14a. For Cr

with S D 3=2 there are four spin

levels and therefore three S D 1 transitions. As shown in Fig.6.9,theabsorp-

tion spectrum will vary according to the orientation of the magnetic ﬁeld vector

H and the axis of symmetry of each equivalent magnetic complex, in this case,

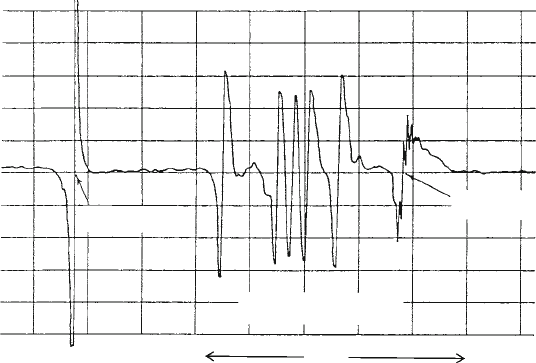
290 6 Electromagnetic Properties

super-hyperfine

structure

H → (100 Oe/div) →

DPPH

3352 Oe

1.0

0.8

0.6

0.4

0.2

Fig. 6.9 Sample EPR spectrum of the uncommon Ti





ion in Rb alum with  D 9:4 GHz.

Relaxation time measurements were carried out by the saturation method described in [18]and

Chap. 6 of [4]. Six of the twelve orientations of the orthorhombic Ti

 6H

O site are resolved.

Note also the hyperﬁne structure that appears at higher ﬁelds, possibly due to interactions with

neighboring nuclei

from the 12 differently oriented the Ti

complexes in Rb alum. A straightforward

analytical procedure allows the determination of the relevant parameters of the spin-

Hamiltonian, g

, g

,andD (and E, if symmetry is lower than axial). From these

values, estimates of the spin–orbit coupling constant  and the excited-state orbital

splitting ı can be made following the reasoning outlined in Sect. 5.1.3.

Table 6.2 summarizes data extracted from EPR studies carried out by early re-

searchers at X-band microwave frequencies (10 GHz). The results of this work

were compiled in review articles by the British pioneers [15, 16]. Interpretation of

spectra can be challenging when higher-order effects cause ﬁne structure in the split-

ting of energy levels. Interaction terms are added to the spin-Hamiltonian to account

for spin couplings between electron and nuclei. In most cases, the energies are great

enough to produce discernible lines in a resolved spectrum that allows the measure-

ment of additional coupling constants.

One complication that can arise involves the orientation of local crystal-ﬁeld site

symmetry relative to the main symmetry axes of the crystal lattice. For the standard

case of a cubic-lattice hosting complexes of axial crystal-ﬁeld symmetry aligned

with h111i axes, lines from four different site orientations appear in the spectrum,

merging only when H is along one of the h100i axes where they appear identical.

An example of an unusual situation that illustrates this point is shown in Fig. 6.9

for the sample spectrum of Ti

in Rb alum [14]. From an orbital singlet, Ti

has only one Kramers doublet transition (C1=2 $1=2), and there should be a

maximum of only four spectral lines if the site symmetry is axial and h111i-axes

aligned, i.e., one line for each h111i direction. Several spectral lines are observed

6.2 Gyromagnetic Resonance and Relaxation 291

Table 6.2 3d

Transition group data

Free ion Ti





1



154 104 87 85 – –100 –180 –335 –852

55 57

Hund term

3=2

5=2

9=2

3=2

High spin – – –





























































Lowspin– –––– –

















































S(hs) 1=2 1 3=2 2 5=2 2 3

2 1 1

(ls) 1 1

2 0 1

hgi 0to

1:9

1:9 1:9–21:9–2 2>3to

7

>4 >2:25 2–2:5

Data obtained from W. Low, Paramagnetic Resonance in Solids, (Academic, New York, 1960),

Table XIX and J.S. Grifﬁth, The Theory of Transition-Metal Ions, (Cambridge University Press,

Cambridge, 1961), Appendix 6

Low-spin states can occur in lower symmetry crystal ﬁelds that split the E

degeneracy sufﬁ-

ciently to cause a violation of Hund’s rule by creating a spin pair in the lower e

state

because the local crystal ﬁeld symmetry is of lower symmetry (orthorhombic) than

the alum lattice (cubic) and none of the site axes coincide with the lattice h111i axes.

The net result is spectra with a maximum of 12 lines representing 12 equivalent but

distinguishable complexes.

Paramagnetic resonance can be observed in any structure where isolated mo-

ments are induced into precession about a magnetic ﬁeld. Most of the early work

was carried out with single-crystals of water-soluble salts of the transition met-

als. Because of their high melting points, bulk single-crystal oxides require exotic

crystal-growth facilities and superior artistry. Nonetheless they became a host for

vigorous research in quantum electronics that led to the invention of the microwave

ampliﬁer known as the maser in three-level Cr

in Al

(ruby) [17], which was

the precursor of the ruby laser.

One of the drawbacks of EPR is the necessity for cryogenics. In magnetically di-

lute specimens, maximum utilization of the low spin densities is essential, and spin

populations of the ground state are largest at low temperatures. Moreover, signal

intensities are also enhanced by resonance linewidth narrowing that is encouraged

by longer spin–lattice relaxation times 

at low T . This concern is particularly im-

portant in compounds containing fast-relaxing ions for which Raman and Orbach

processes are dominant at higher temperatures. Conversely, line broadening be-

comes a limitation on the useful concentrations of magnetic ions due to spin–spin

relaxation or decoherence time 

that shortens in proportion to the separation

between magnetic ions. This effect has motivated line-shape studies as a function of

concentration [18].