Dionne G.F. Magnetic Oxides

Подождите немного. Документ загружается.

292 6 Electromagnetic Properties

Although not of much use for diagnostic purposes, magnetic resonance in

exchange-coupled systems can be observed at room temperature, and therefore can

be effective in controlling magnetic permeability and rf propagation parameters. In

more recent years these magnetic dipole effects have contributed to the enhancement

of electrical permittivity discussed in Chap. 7 that forms the basis of magnetoop-

tical phenomena originating from electric-dipole transitions in transition-metal

compounds, including the magnetic semiconductors, e.g.,



GaMn



As.

6.2.2 Ferromagnetic Resonance

To this point in the discussion, magnetic resonance has been viewed classically as a

moment vector precessing about a dc magnetic ﬁeld vector, stimulated by the mag-

netic ﬁeld of an electromagnetic signal directed normal to the dc ﬁeld. Within the

same vector constraints and through use of the spin-Hamiltonian approximation, a

quantum electronics model can be applied to a paramagnetic system of Kramers

doublets split in the dc magnetic ﬁeld. However, for magnetically ordered systems

where the individual moments are tightly coupled into alignment by strong restor-

ing forces from the exchange ﬁelds, the magnetic ions cannot easily be analyzed as

individual quantum entities. There is no convenient QM analog to the precessing

collective magnetic moment (or magnetization) vector M in the case of a ferromag-

net, although it could be argued that the minimum resonance energy transfer in the

coupled system is a photon of energy gm

H , representing the 180

reversal of a

single electron spin (S

D˙1). The subject of Kramers doublets in an exchange

ﬁeld is examined in Chap. 7.

For ferromagnetic resonance, the system is treated conventionally following the

basic classical model of a magnetization vector M comprising collective magnetic

moments (†m) with gyromagnetic constant  as deﬁned previously (and presumed

to be positive unless a sign change is required) for paramagnetism. The Larmor

precession relation of (6.37) can then be applied to FMR as

D .M  H

/; (6.42)

with the appropriate value of  for the individual magnetic moments in the collec-

tive precessing group and the effective internal dc magnetic ﬁeld H

. This result

is based on the assumption that the uniformity of the precession is not affected by

the presence of spin waves that will be introduced later. For the present, we shall

conﬁne the discussion to the basic uniform precession case and proceed to examine

the effects of magnetocrystalline and shape demagnetizing ﬁelds on the resonance

frequencies of single-crystal specimens of ellipsoidal geometry.

For a ferro- or ferrimagnetic specimen, the effective magnetic ﬁeld for resonance

is usually not equivalent to the internal dc ﬁeld H

, because the demagnetizing

factors from the transverse directions inﬂuence the value of the rf ﬁeld. Only in

6.2 Gyromagnetic Resonance and Relaxation 293

the case of a semi-inﬁnite medium or a thin ﬁlm (where N

D N

 0,and

 1) that is crystallographically isotropic can we write

D H

D H  N

4M  H  4M: (6.43)

The general relation for !

D H

is found from(6.42) by treating all magnetic ﬁelds

as vectors, with demagnetization factors introduced as tensors. Because the details

have been documented in many publications, beginning with the seminal work of

Kittel [19] and expounded in [20]and[21], they will not be repeated here. However,

speciﬁc solutions for some common situations will be reviewed.

For a fully magnetized specimen with H and M aligned with the z-axis, Kittel

determined that

D 



ŒH C .H

 H

/ C .N

 N

/4M

ŒH C



 H





 N



4M 



: (6.44)

The subscripts x and y refer to the two major axes orthogonal to the z direction of

H in the coordinate system selected. Note that effective H

reduces to (6.43)when

all of the demagnetizing factors approach zero, and N

! 1. For particular cases,

the appropriate relation for H

from the list in Appendix 5D of Chap. 5 can be

inserted directly into (6.44). The appropriate shape demagnetizing factors N

can

be determined from the analysis summarized in Sect. 1.1.3.

For resonance to occur, H

must have a component in the x–y plane, but values

of the N

and N

factors will be sensitive to its exact direction within the plane.

Applied to the limiting case of a thin ﬂat plate with N

D 1,andN

, N

D 0,

and H

terms ignored, (6.44) can be expressed as

D ŒH.HC 4M /

.H in plane/

D .H 4M / .H normal to plane/: (6.45)

For a long slender cylinder aligned with the z-axis, N

, N

D 1=2,andN

D 0.

The resonance frequency is then

D .HC 2M / .H parallel to long axis/;

D ŒH.H 2M /

.H normal to long axis/: (6.46)

For a sphere, N

, N

D 1=3, and the shape demagnetizing factors of (6.44)

cancel, so that

D H: (6.47)

Because the effect on the resonance condition from anisotropy ﬁelds varies with

crystallographic orientation, the relations include the H

terms only when single

crystals are involved. For randomly oriented crystallites in ceramics, H

serves to

produce inhomogeneous broadening of the resonance line. Measurements are usu-

ally carried out by rotating the magnetic ﬁeld H in a particular plane, with the

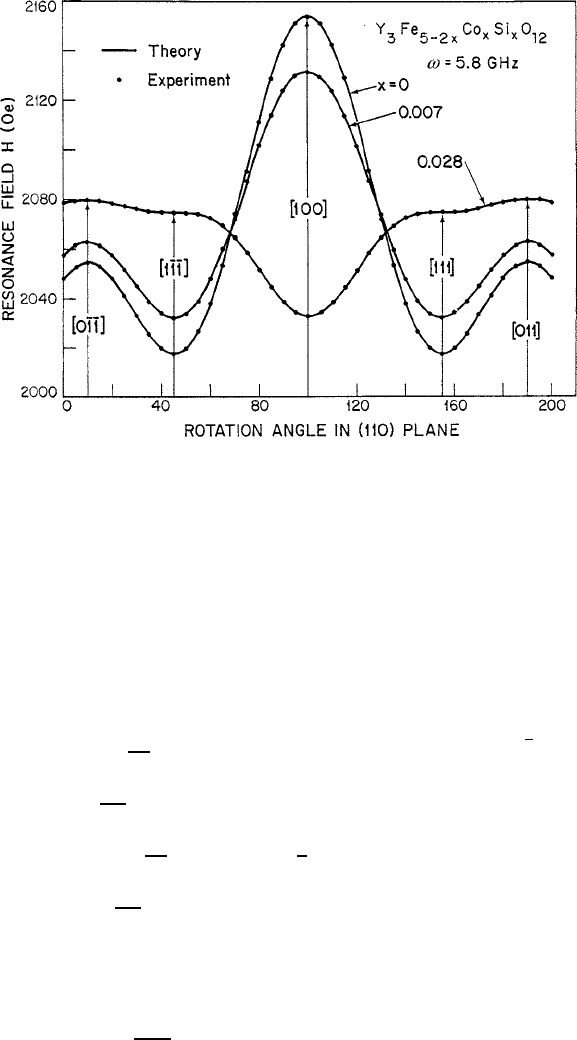
294 6 Electromagnetic Properties

Fig. 6.10 Determination of magnetocrystalline anisotropy ﬁelds from measurements of the reso-

nance magnetic ﬁeld at frequency  D 5:8 GHz. Direction of H is rotated through the [110] of the

cubic garnet lattice to expose the inﬂuence of Co

on the anisotropy constants [22]

resonance frequency displayed as a function of angle relative to a major axis of

symmetry. Figure6.10 offers an example of the variation of resonance ﬁeld H for a

ﬁxed !

D 5:8 GHz as it is rotated in a f110g plane, passing through h100i “hard,”

h111i “easy,” and “intermediate” h110i axes [22]. The effects of small concentra-

tions of Co

ions on the anisotropy ﬁelds are strikingly illustrated. For this case,

as a function of angle ı referenced to the h100iaxis is expressed by

D 

H C



2  sin

ı  3 sin

2ı





sin



6 cos

ı  11 sin

ı cos

ı C sin





H C



2  4 sin

ı 

sin

2ı







.sin

ı cos



3 sin

ı C 2



;

: (6.48)

From (6.48), we can extract relations for H along the h100i.ı D 0/, h112i

.ı D 35

/, h111i .ı D 55

/,andh110i .ı D 90

/ axes:

D 



H C



H parallel to

100

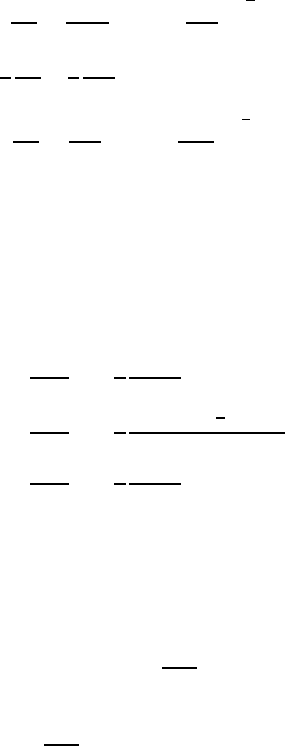
6.2 Gyromagnetic Resonance and Relaxation 295

D 



H 

18M



H 



H parallel to

112

D 



H 





H parallel to

111

(6.49)

D 



H C



H 



H parallel to

110

The H

relations for three other common families of planes in a cubic system, i.e.,

f100g, f111g,andf112g, are listed in Appendix 5D of Chap. 5.

A stress-induced shift in the resonance frequency ı!

(or ﬁeld ıH ) can be

used to determine the magnetostriction constants 

100

and 

111

[23–26]. For these

measurements, a spherical specimen geometry remains convenient to cancel shape

demagnetizing effects. The relevant relations are expressed as



100

D

ıH

100



;



100

Š



ıH

110

ıH

100





; (6.50)



100

Š

ıH

111



;

where  is the uniaxial compressive stress directed along the axis of the magnetic

ﬁeld.

For completeness, we state the expression for the uniaxial case with anisotropy

constant K

(which can apply to a grain-oriented polycrystal as well as a single

crystal), according to

D 



H C

cos



; (6.51)

and

D 



H C



.H parallel to axis of symmetry/; (6.52)

which accounts for the very large resonance frequencies of the M-type hexagonal

ferrites.

6.2.3 Uniform Precession Damping

For exchange-ordered systems, we must also include the paramagnetic resonance

damping mechanism of spin–lattice relaxation. However, the situation can be

simpliﬁed somewhat because we can neglect spin–spin decoherence in the uniform

precession case. From the discussion in Sect. 1.5 and Appendix 1A of Chap. 1,

the precessional relations with Bloch–Bloembergen longitudinal and transverse

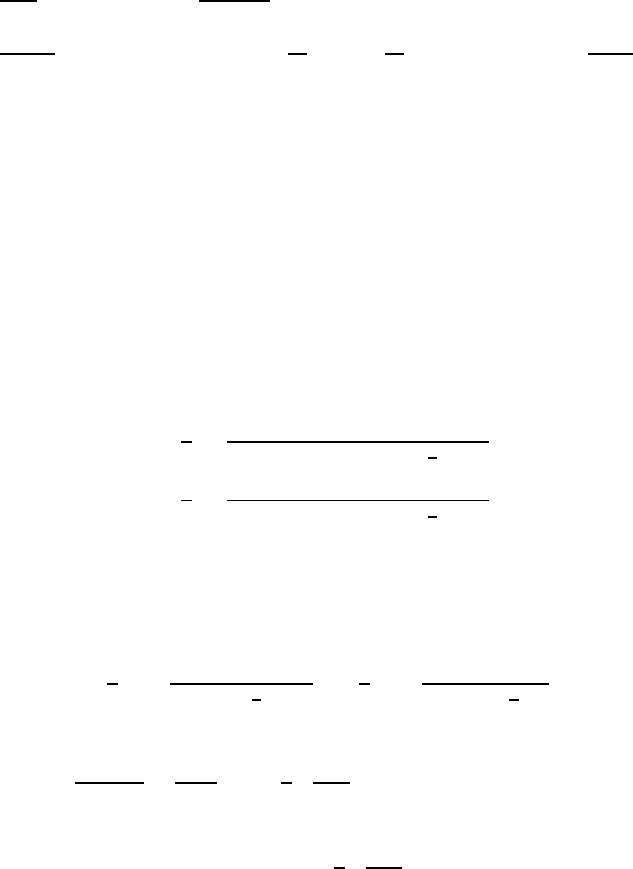
296 6 Electromagnetic Properties

damping ([15,16] of Chap. 1) can now be written as

D .M  H



 M



x;y

D .M  H

x;y

M

x;y





C f./





Š .M H

x;y



x;y

2

;

(6.53)

where 

 

and f./ 1=2 when spins are magnetically ordered in a “uniform

precession” mode with all moments locked tightly in phase throughout the medium.

Longitudinal relaxation back to the z-axis would then be pictured as an inwardly

spiraling precession.

In the uniform precession mode, the spin–spin decoherence time 

is assumed

to be inﬁnite at temperatures far from the Curie temperature. Under this condition,

relaxation and line broadening are determined by spin–lattice coupling, which is

characterized by .2

1

, since we can assume that the canting angle   0.

Recalling the discussion of paramagnetic relaxation in Chap. 1, we can examine

the effect of 

 2

in the susceptibility relations of (1.84) by assuming that



1

 ! D H . In the laboratory frame of reference,



M

.H

 !/

.!/

C .H

 !/



;



M

!

.!/

C .H

 !/



: (6.54)

At resonance, the saturation effect resulting from increasing H

can be seen by

inspection after the relations are simpliﬁed to



Š 0



M

!

.!/



M

H

.H /

: (6.55)

and



.0/

H

 1 



H



.for H

 H / ; (6.56)

where

H

D H

1 C



H



is the broadened half-linewidth at resonance. Note that 

far from resonance is

not reduced by H

and the intrinsic half-linewidth should still be characterized by

H (or H

to distinguish it from other broadening mechanisms). In this sense, the

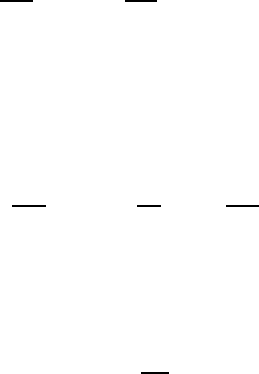
6.2 Gyromagnetic Resonance and Relaxation 297

departure of the resonance line from a rigorous Lorentzian shape is of consequence

only near the line center.

It is important to point out two other models of damping that are used in the

derivation of the complex susceptibility relations (see Appendix 6A). Historically,

Landau and Lifshitz [27] were the ﬁrst to propose an FMR damping term, which is

expressed as





damp

D



M  .M  H

/; (6.57)

where  is a semiempirical damping parameter, a total relaxation time  can be

deﬁned as  D M=H

. It should be noted that in this formalism   

of the

Bloch–Bloembergen model, so that  is mathematically equivalent to 2

in the

uniform precession mode of an exchange-ordered system.

A later version of the damping equation was introduced by [28]:





damp

D



M 



; (6.58)

where ˛ is the damping parameter. For constant M , it can be shown that (6.57)

effectively reduces to (6.58) provided that ˛ D =M [29]. Near the resonance

frequency, the effective relaxation time can be approximated by (see Appendix 6A)

 D

˛!

: (6.59)

Although these models are usually treated as equivalent, the Gilbert form in (6.58)is

more suitable for the derivation of the rf susceptibility tensor in Sect. 6.4. Relaxation

damping of rf signals can be affected greatly in ferrimagnets by even small amounts

of fast-relaxing ions and other factors that will be reviewed. These effects, however,

must ﬁrst be seen in the context of the total resonance linewidth within which they

are often obscured.

6.2.4 Inhomogeneous Resonance Line Broadening

In the foregoing analyses of magnetic resonance damping, the half-linewidth H is

proportional to the effective relaxation rate 

1

, which is a combination of 

1

and



1

. Before examining the factors that inﬂuence the values of 

1

and 

1

in mag-

netic lattices, the subject of inhomogeneous line broadening must be introduced.

Recalling the discussion in Sect. 1.5, we recognize that an inhomogeneously broad-

ened line does not have the Lorentzian shape assumed in the Bloch–Bloembergen

formalism. A Gaussian distribution function is more appropriate. Consequently, for

the purposes of using the theory to interpret measurements, only the intrinsic ho-

mogeneous component H

of the total H can be applied in (6.56)and(6.57).

298 6 Electromagnetic Properties

Despite their corrupting effect, however, the inhomogeneous broadening can pro-

vide useful information for characterizing polycrystalline specimens.

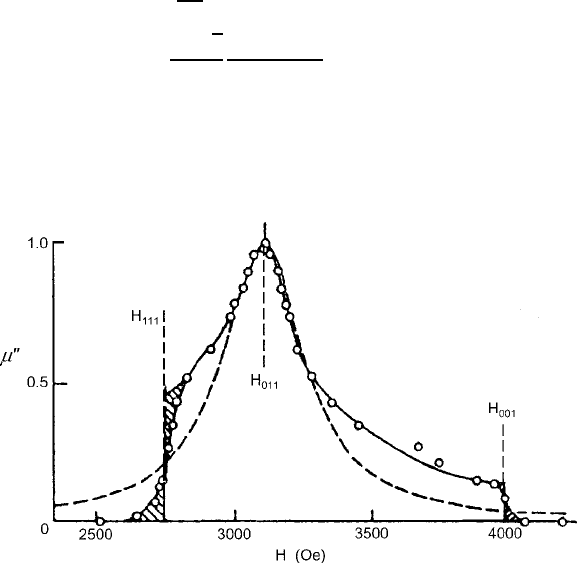
In a polycrystalline ceramic body, inhomogeneities can impact the shape and

width of magnetic resonance lines. The ﬁrst is the random crystallographic ori-

entation of individual crystallites or grains. Where the various symmetry axes are

dispersed, the resonance ﬁelds of each grain will vary accordingly in proportion to

. An actual measurement for cubic YIG that reveals dramatically the nature of

these effects is presented in Fig. 6.11 from the work of Van Hook and Euler [30].

Schloemann [31,32] and Geschwind and Clogston [33] examined the question and

produced analytical results that have been helpful in characterizing the anisotropy

and grain orientation of ferrites. For a spherical specimen, anisotropy contributions

to the half-linewidth were deﬁned according to

H



 2K

;

H

8

.2K

4M

G M

 2K

; (6.60)

where G is a shape factor that is dependent on the ratio !=4M

. For YIG at room

temperature, K

 40 Oe and 4M

D 1;780 G. Here the low K

case

applies and yields H

 8 Oe, in agreement with measured results from dense

Fig. 6.11 Experimental example of an inhomogeneously broadened FMR permeability of a V-In

diluted yttrium–iron garnet ceramic specimen. Individual crystallites (grains) are randomly ori-

ented and have narrow Lorentzian resonance lines along favored axes. The overall width of the

combined resonances is determined by the extremes at H

001

and H

111

. The peak occurs at H

011

which is the most numerous symmetry axis of a cube. The dashed line with the extended tails is

a homogeneous equivalent of the measured result, indicating that the effective Lorentzian width is

considerably smaller than the measurement would suggest. Figure reprinted from [30] with per-

mission.

 1969 y the American Institute of Physics

6.2 Gyromagnetic Resonance and Relaxation 299

ceramic specimens. In polycrystalline bodies the saturation magnetization M

speciﬁed because M can assume various values of partial magnetization. An exam-

ple of how these relations can be used as design aids for determining variations of

with composition will be given in Sect. 6.2.5.

A second inhomogeneous broadening effect is caused by the local variation of

magnetization due to compositional ﬂuctuations, crystallites of different chemical

phase, or most commonly, air porosity. Schloemann [31,34] and Sparks [35] mod-

eled this effect, with the result that a porosity contribution to H was deﬁned as

H

D ˇ.4M



1  p



; (6.61)

where ˇ1 [36]. With(6.1)and(6.2), the total FMR half-linewidth can be expressed

as the sum of relaxation rates in linewidth form as

H  H

C H

; (6.62)

where each individual grain provides an intrinsic Lorentzian H

contribution to

the inhomogeneously broadened Gaussian result that then comprises the frequency

spread of smaller intrinsic lines. This is manifested in Fig. 6.11. It should be pointed

out here that the relations for the different linewidth contributions can be used ef-

fectively in combination with the approach-to-saturation theory for characterization

of magnetic polycrystals [37].

To assist in the magnetic loss characterization away from the resonance line cen-

ter, Patton [38] and Vrehen [39] measured an effective linewidth by a manipulation

of (6.54)for

. With !  H

and !, the operating point is far from both the

line center and the high-frequency edge of the inhomogeneous loss manifold, and



M

!

(6.63)

for circular polarization. If the effective half-linewidth is now deﬁned as H

eff

!=,(6.63) can be re-expressed as

H

eff

4

.4M



!





 2





(6.64)

for a typical microwave device application. As a measure of loss, H

eff

is propor-

tional to the reduced value of the  outside of the broadening range and is therefore

small enough to resemble the intrinsic H

, as illustrated by the data for a system-

atic range of garnet compositions with monotonically changing K

values [38]

in Fig. 6.12. With H

eff

seen in the context of spin–lattice relaxation, we can more

clearly examine the fundamental factors that inﬂuence its true value.

300 6 Electromagnetic Properties

Fig. 6.12 Effective linewidth of polycrystalline garnet specimens of composition Y

32x

5x

with a range of anisotropy ﬁelds. Figure reprinted from [38]

with permission.

 1969 by the American Physical Society. http://link.aps.org/doi/10.1103/

PhysRev.179.352

6.2.5 Fast-Relaxing Ion Effects

Transmission of microwave energy with minimum relaxation loss is critical to the

efﬁciency of ferrites used as propagation media. Ferrimagnetic resonance (FMR)

relaxation is reﬂected in the intrinsic half-linewidth (H

), and can be an essential

mechanism in the loss of signal intensity. For magnetically ordered spin systems,

H

has been treated as a direct function of the spin–lattice relaxation rate 

1

with-

out consideration of its temperature dependence or the disposition of the phonon

population. These latter effects were highlighted when measurements of loss in

rare-earth (RE) iron garnets revealed a monotonic decrease in H

with reducing

temperatures, but interrupted by a peak in the vicinity of T  50 K that is propor-

tional to the concentration of RE ions [40, 41].

As listed in Table 6.3, 

1

can be sensitive to temperature through a variety of

mechanisms. One effect that was not introduced in the discussions of paramagnetic

relaxation was the phonon “bottleneck.” If the phonons that are created when the

spin relaxes to its ground state are not in thermal equilibrium with the total lattice

“bath,” an additional relaxation between phonon and lattice must take place. As a re-

sult, the effective value of 

increases accordingly, and because the nonequilibrium

condition between phonon and bath is also temperature dependent, the expressions

6.2 Gyromagnetic Resonance and Relaxation 301

Table 6.3 Gyromagnetic relaxation rate–linewidth relations

Precessing system Theory 

1

D H



1



EPR Bloch–Bloembergen (B–B)

2

1

C 

1

FMR uniform precession Bloch–Bloembergen (B–B)

2

1

Landau–Lifshitz (L–L) 

Gilbert (G) ˛H

FMR uniform precession

with spin waves

Bloch–Bloembergen (B–B)

2

1

C 

1



Spin–lattice relaxation time, 

spin–spin decoherence time (via dipolar interac-

tions), 

spin–spin decoherence time (via spin waves)

for 

must also account for this inﬂuence. This subject has been examined by Van

Vleck [42], Faughnan and Strandberg [43], and Stoneham [44], and a review can be

found in Standley and Vaughan [45]. However, the approach followed here is based

on that of de Gennes et al. [40]. In terms of the phonon quantum number n



eff

D 



C 1



C n



C 1



 n

D 



C 1



; (6.65)

where

D Œexp .„!=kT /  1

1

D exp .„!=kT / Œ1  exp .„!=kT /

1

: (6.66)

For the iron sublattices, where 

D 

eff





1  exp .„!=kT /

1 C exp .„!=kT /









„!

2kT





; (6.67)

where it is assumed that „!  kT . For an assumed direct process, we can ap-

ply a temperature dependence based on (6.67) to the iron intrinsic half-linewidth

according to

H

D .

1



„!

2kT



.

1

D 

1



„!



; (6.68)

where n is a data ﬁtting parameter that can exceed the theoretical value of unity.

Where rare-earth or other ions that exchange couple signiﬁcantly to the Fe sub-

lattices, but weakly enough to each other as to be treated as paramagnets attached

to the net iron moments, an additional relaxation rate 

1

must be considered. If re-

laxation rates are transition probabilities as depicted in Fig. 6.13, a straightforward

addition of the respective relaxation rates 

1

and 

1

for the net iron and RE ions

can be used according to [46].



C 



; (6.69)