Deza M.M., Laurent M. Geometry of Cuts and Metrics

62

Chapter

5.

The

Correlation Cone

and

{O,

1 }-Covariances

Proof. For S

~

V

n

,

set

A

S

:=

n

Ai

n

n(f2\Ai).

iES

i'/.S

Then,

Ai

n

Aj

= U

AS,

f2

= U

AS,

and

Al

U

...

U

An

= U

AS.

S<;;Ynli,jES

S<;;;Vn

S<;;;VnIS"e0

Therefore,

P = L /L(A

S

)7r(S),

S<;;;VnIS"e0

with

/L(AS)

~

0 for all

S.

Hence, (/L(AS) I 0

=f

S

~

V

n

)

is

a feasible solution

to

the

programs

(5.4.1)

and

(5.4.2),

with

objective value /L(A

1

U

...

U

An).

This

shows

the

result. I

Using linear

programming

duality,

we

can reformulate

Zmin

and

Zmax.

Namely,

(5.4.4 )

Zmin

=

max(wT

pi

w

T

7r(S)

:S

1 for all S, 0

=f

S

~

V

n

)

and,

as can be easily verified,

it

suffices to consider

in

(5.4.4)

the

vectors w for

which

the

inequality w

T

x

:s

1 defines a facet of

COR~.

Similarly,

(5.4.5)

where

it

suffices to consider

the

vectors w for which

the

inequality w

T

x

~

1

defines a facet of

the

polytope Conv({7r(S)

10

=f

S

~

V

n

})

(which is

distinct

from

COR~

since it does

not

contain

the

origin).

Therefore, every valid inequality for

COR~

yields a lower

bound

for /L(AI U

...

U

An)

in

terms

of

the

joint

probabilities Pij = /L(Ai n A

j

).

Many

such inequal-

ities are known;

cf.

Part

V for a presentation

of

large classes of such inequalities.

As

an

illustration,

we

now mention a

few

examples of such inequalities

together

with

the

corresponding lower bounds.

A first observation

is

that

n L

Pi

- 2 L Pij n L

Pi

- 2 L Pij

l<i<n l<i<j<n

'"

l<i<n l<i<j<n

----'=-=""'l

!!±l-'2-;-I-:-J

r=-!!±l"::=2

';-:11,.o.=.-:s

~

>'s:s

----'=-=

__

--=--'.O..;=-_

0"eS<;;;Vn

n

for any decomposition P = L >'S7r(S)

with

>'5

~

0 for all

S.

(This

follows

0"eS<;;;Vn

from (4.3.6),

via

the

covariance mapping.) From

the

definition

of

Zmin,

Zmax

and

from

Proposition

5.4.3,

we

obtain:

5.4

The

Boole

Problem

63

n L

Pi

- 2 L Pij

(5.4.6)

l<i<n

l<i<j<n

L9'lH9'll

::;

/L(Al U

...

U

An)

n L

Pi

-2

L Pij

l<i<n

l<i<j<n

n

Consider

now

the

inequality:

(5.4.7)

2k

L

Pi

- 2 L Pij::;

k(k

+ 1).

l'Si<j'Sn

It

is valid for

the

correlation

polytope

CO~

if

1

::;

k

::;

n -

1.

(Moreover, it

is

facet defining if 1

:'S

k

:'S

n - 2 and n

2:

4.

Indeed, it corresponds (via the covariance

mapping) to the inequality:

L Xij +

(2k

+ 1 -

n)

L Xi,n+l

:'S

k(k

+ 1)

l:Si<i:Sn l:Si:Sn

which defines a facet of

CUT~+l

if 1

:'S

k

:'S

n - 2 and n

2:

4;

see

Theorem 28.2.4.)

This

yields

the

following lower

bound

for /L(A

1

U

...

U An):

(5.4.8)

for each k, 1

::;

k

::;

n

-1.

The

bound

(5.4.8) was found

independently

by

several

authors,

including

Chung

[1941]' Dawson

and

Sankoff [1967],

Galambos

[1977].

Note

that

(5.4.8) coincides

with

the

lower

bound

of

(5.4.6)

in

the

case n = 2k.

The

case k = 1

of

(5.4.8) gives

the

bound

L

Pi

- L Pij::; /L(A

1

U

...

U

An)

which

is a

special

case

of

the

Bonferroni

bound

(5.4.14)

mentioned

below. More

generally, given integers

b

1

,

...

,b

n

and

k

2:

0,

the

inequality:

(5.4.9)

L b

i

(2k + 1 - bi)Pi - 2 L b;bjPij::;

k(k

+ 1)

is valid for

CO~,

which yields

the

bound:

k(k

1 ) ( L Pibi(2k + 1 - b

i

) - 2 L b;bjPi

j

)::;

/L(Al U

...

U

An)·

+ 1

l'Si'Sn

l'Si<j'Sn

To

see the validity of inequality (5.4.9), note

that

it can alternatively be written as

(5.4.10)

(

L

biPi -

k)

( L biPi - k -

1)

2:

0

l:Si:Sn l:Si:Sn

with the convention

that,

when developing the product, the expression PiPj

is

replaced

by the variable

Pij (setting Pii = Pi).

64

Chapter

5.

The

Correlation

Cone

and

{O,

1

}-Covariances

Remark

5.4.11.

The

inequality

(5.4.9)

(or

(5.4.10))

(or

special

cases

of

it)

was

considered

independently

by

many

authors;

among

others,

by

Kelly

[1968],

Davidson

[1969]'

Yoseloff

[1970],

McRae

and

Davidson

[1972]'

Kounias

and

Marin

[1976],

Erdahl

[1987],

Mestechkin

[1987],

Pitowsky

[1991].

The

inequal-

ity

(5.4.10)

appears

in

Figure

5.2.6;

it

corresponds

(via

the

covariance

mapping

and

after

setting

b

n

+

1

:=

2k

+ 1 -

2:7=1

bi)

to

the

inequality:

(5.4.12)

bibjXij

::;

k(k

+ 1),

l~i<j~n+l

which

is

valid

for

the

cut

polytope

CUT~+l.

In

order

to

help

the

reader

under-

stand

how

this

inequality

relates with

further

inequalities

to

be

introduced

later,

let

us

mention

that

the

class of inequalities of

the

form (5.4.12)

contains

the

hypermetric

inequalities

(to

be defined in Section 6.1)

as

special instances. More precisely, (5.4.12)

is a

hypermetric

inequality

if k =

O.

Moreover, (5.4.12) is a switching of a

hypermetric

inequality

if

the

sequence b

l

,

...

, b

n

+

1

has

gap

1.

(The

notions

of switching

and

gap

will

be

defined

later

in

Sections 26.3

and

28.4.) I

Generalization

to

Higher

Order

Correlations.

Clearly, much

of

the

above

treatment

can

be

generalized

to

higher

order

correlations. Namely, let I

be

a family of

subsets

of V

n

. Given a

subset

S of V

n

, its I-correlation vector

nI(S)

E

ffi.I

is defined by

nI(Sh

= 1 if I

~

Sand

nI(Sh

= 0 otherwise, for all I E

I.

Then,

the

cone

CORn

(I)

(resp.

the

polytope

COR~(I))

is defined as

the

conic hull (resp.

the

convex hull) of all

I-correlation

vectors n

I

(S) for S

~

V

n

.

Given

an

integer 1

:<:::

m

:<:::

n,

let

I<m

denote

the

collection of all

subsets

of

Vn

of

cardinality

less

than

or

equal

to

m.

H~nce,

I<2 consists of all singletons

and

pairs

of

elements

of

Vn

and,

therefore,

COR

n

(I<2)

and-

COR~(I<2)

coincide, respectively,

with

CORn

and

COR~.

- -

For

I = 2Vn, which consists of all

subsets

of V

n

,

COR~(2Vn)

is a simplex

and

COR

n

(2

Vn

) is a simplex cone,

both

of dimension 2

n

-1.

This

implies, in

particular,

that

every

correlation

polytope

COR~(I)

arises as a

projection

of

the

simplex

COR~(2Vn)

(namely,

on

the

subspace

ffi.I).

The

result

from

Proposition

5.3.4

extends

easily

to

the

case of

arbitrary

I-correlations.

Proposition

5.4.13.

Let

I

be

a

nonempty

collection

of

subsets

of

{I,

...

,

n}

and

let

P

=

(PIhEI

E

ffi.I.

The following assertions are equivalent.

(i)

P E

CORn(I)

(resp. P E

COR~(I)).

(ii) There exist a measure space (resp. a probability space)

(0,

A,

J.L)

and

events

AI,

.

..

,

An

E A such

that

PI = J.L(niEI

Ai)

for all I E

I.

I

A

more

general version of

the

Boole problem consists of finding

estimates

for

the

quantity

J.L(A

I

U

...

U

An)

in

terms

of

the

joined correlations J.L(niEI

Ai)

for I E

I.

There

is

an

obvious

analogue

of

Proposition

5.4.3, where

the

bounds

Zmin

and

Zmax

are

now

in

terms

of

the

polytopes

COR~(I)

and

Conv({nI(S)

10

=f.

S

~

V

n

})

(instead

of

COR~

and

Conv({n(S)

10

=f.

S

~

V

n

})).

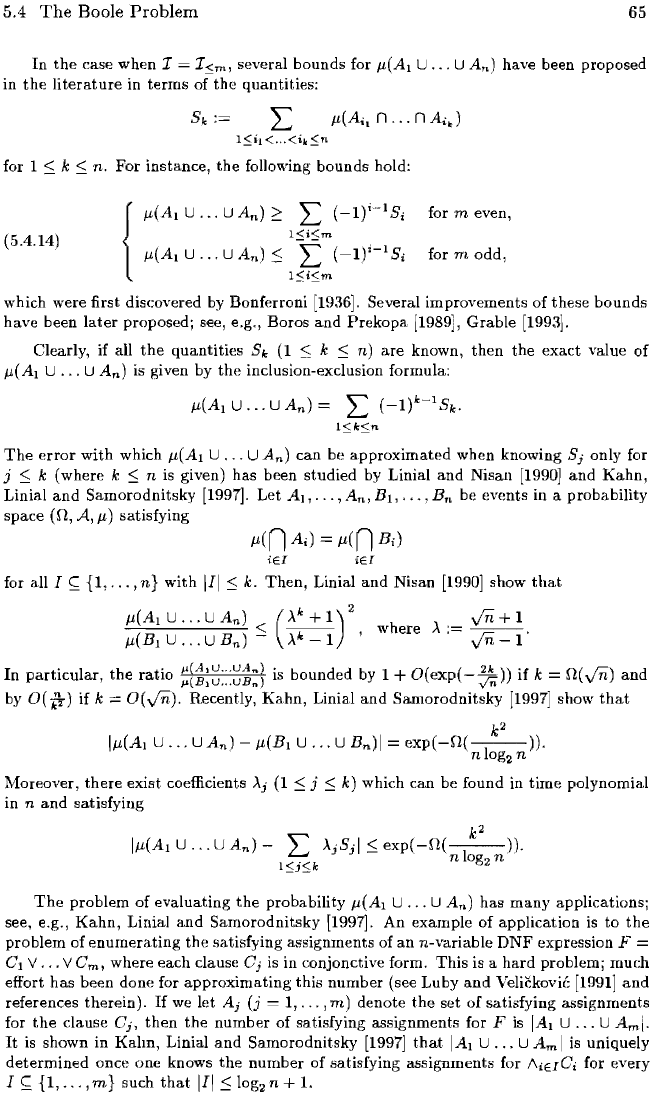
5.4

The

Boole Problem

65

In

the

case when I several

bounds

for tL(A

I

U

...

U

An)

have been proposed

the

quantities:

for 1

:s;

k

:s;

n.

For instance,

the

following bounds hold:

(-I);-IS;

for m even,

(5.4.14)

(-I);-IS;

for m odd,

which were first discovered by Bonferroni [1936]. Several improvements

of

these

bounds

have

been

later

proposed; see, e.g., Boros

and

Prekopa

[1989], Grable [1993].

Clearly, if all

the

quantities

S"

(1

:s;

k

:s;

n)

are

known,

then

the

exact

value

of

tL(A

j

U

...

U

An)

is given by

the

inclusion-exclusion formula:

The

error

with

which tL(AI U

...

U

An)

can

be

approximated

when knowing

Sj

only for

j

:s;

k (where k

:s;

n

is

given) has been studied by Linial

and

Nisan

[1990]

and

Kahn,

Linial

and

Samorodnitsky

[1997].

Let

.'1.1,

...

,

A.

n

, B

1

,

...

,Bn

be

events in a probability

space (D,

A,

tL)

satisfying

iEI

for all I

~

{I,

...

,

n}

with

III

:s;

k.

Then,

Linial

and

Nisan

[1990]

show

that

tL(A1U

...

UA

n

)

(""+1)2

h \

'--;---"----=--:-:s;

-k--

,

were

"

tL(B

I

U

...

U

Bn)

,,-

1

In

particular,

the

ratio

:i~:

~:::~~:l

is

bounded

by 1 + O(

exp(

-

fo})

if

k D(

J1i)

and

by

O(

Fr)

if k

O(

J1i).

Recently,

Kahn,

Linial

and

Samorodnitsky

[1997]

show

that

ItL(AI U

...

U

An)

- tL(B

I

U

...

U

Bn)1

=

Moreover,

there

exist coefficients

"j

(1

:s;

j

:s;

k) which can be found in

time

polynomial

in

n

and

satisfying

The

problem

of

evaluating

the

probability tL(A

l

U

...

U

An)

has

many

applications;

see, e.g.,

Kahn,

Linial

and

Samorodnitsky

[1997]. An example

of

application is

to

the

problem

of

enumerating

the

satisfying assignments of

an

n-variable

DNF

expression F

G

1

V

...

vGrn, where each clause G

j

is

in conjonctive form.

This

is a

hard

problem; much

effort

has

been done for

approximating

this number (see Luby

and

Velickovic

[1991J

and

references

therein).

If

we let

Aj

(j

= 1,

...

,

m)

denote

the

set

of

satisfying assignments

for

the

clause Gj,

then

the

number

of

satisfying assignments for F

is

IAI

U

...

U Ami.

It

is

shown in

Kahn,

Linial

and

Samorodnitsky

[1997]

that

1.41

U

...

U Ami is uniquely

determined

once

one

knows

the

number

of

satisfying assignments for

AiE1G

i

for every

I

~

{I,

...

,

m}

such

that

III

:s;

log2 n + 1.

M.M. Deza, M. Laurent, Geometry of Cuts and Metrics, Algorithms and Combinatorics 15,

DOI 10.1007/978-3-642-04295-9_6, © Springer-Verlag Berlin Heidelberg 2010

Chapter

6.

Conditions

for

L1-Embeddability

We

present

in

this

chapter

two necessary conditions for L

1

-embeddability, namely,

the

hypermetric

and

the

negative

type

conditions.

There

are

many

other

known

necessary conditions, arising from

the

known valid inequalities for

the

cut

cone;

they

will

be

described

in

Part

V. We focus here

on

the

hypermetric

and

negative

type

conditions.

These

conditions seem indeed

to

be

among

the

most

essential

ones. For instance,

there

are several classes

of

distance spaces for which these

conditions are also sufficient for ensuring L

1

-embeddability; see,

in

particular,

Chapters

8, 19, 24,

and

Remark

6.3.5 for a summary.

Hypermetric

inequalities

will

be

treated

in

detail

for

their

own sake

in

Part

II

and,

as facets

of

the

cut

cone,

in

Chapter

28.

The

present

chapter

is organized as follows.

The

hypermetric

and

negative

type

conditions are

introduced

in

Section 6.1. Several characterizations for

£2-

embeddable

spaces are presented in Section 6.2. We present,

in

particular,

a

characterization

in

terms

of

the

negative type condition

and

Menger's

result

concerning

the

isometric subspaces of

the

m-dimensional Euclidean space. Sec-

tion

6.3 contains a

summary

of

the

implications

that

exist between

the

properties

of

being

L

1

-,

L2-embeddable,

of

negative type, or

hypermetric,

for a

distance

space. We

treat

in

some

detail

in

Section 6.4

an

example:

the

spherical

distance

space, which consists

of

the

sphere

equipped

with

the

usual great circle distance.

This

example

is,

in

a sense,

intermediate

between

£1

and

£2.

Indeed, every

spherical

distance

space is £1-embeddable and,

on

the

other

hand,

the

Euclidean

distance

can

be

realized

asymptotically

as a

limit

of

spherical distances.

The

spherical

distance

space will

be

useful

in

Section 31.3 for

the

positive semidefi-

nite

completion

problem.

6.1

Hypermetric

and

Negative

Type

Conditions

6.1.1

Hypermetric

and

Negative

Type

Inequalities

Let n

2:

2

and

let b

1

,

...

,b

n

be

integers.

We

consider

the

inequality:

(6.1.1)

L bibAj::::: 0

1:<;i<j:<;n

(in

the

variable

dij).

For convenience,

we

introduce

the

following

notation.

Given

68

Chapter

6.

Conditions for L1-Embeddability

b E

lJll

n

, Qn

(b)

denotes

the

vector

of

lJllE

n

defined by

Qn(b)ij

:=

bib

j

for 1 S i < j S n.

Hence,

the

inequality (6.1.1) can be

rewritten

as Qn(b)T d S 0.

When

the

param-

eter

n is clear from

the

context

we

also denote Qn(b) by Q(b).

We

can

suppose

that

at

least two

of

the

b;'s are nonzero; else, Qn(b) °

and

the inequality (6.1.1)

is void.

When

b

i

1,

the

inequality (6.1.1) is called a hypermetric inequality

and,

when

bi

0,

it

is called a negative type inequality.

The

inequality

(6.1.1) is

said

to

be

pure

if

Ibil

= 0, 1 for all i E V

n

.

The

inequality (6.1.8)

is

said

to

be

a k-gonal inequality

if

Ib,l

k holds. Note

that

k

and

bi

have

the

same

parity.

In

particular,

the 2-gonal inequality is

the

inequality

of

negative type (6.1.1),

where

bi

= 1, b

j

-1

and

bh

° for

hE

Vn

\

{i,j},

for some

distinct

i,j

E V

n

;

it

is

nothing

but

the

nonnegativity constraint dij

:::::

0.

The

pure

3-gonal inequality

is

the

hypermetric

inequality (6.1.1), where

bi

= b

j

= 1,

bk

=

-1

and

b"

°

for h E

Vr.

\

{i,j,k},

for some distinct

i,j,k

E V

n

;

it

coincides

with

the triangle

inequality (3.1.1). For f 0,1, the

pure

(2k + f)-gonal inequality

reads:

where i

l

,

...

,ik,

ik+ojI,

...

,jk

are distinct indices

of

V

n

·

As

an

example,

the

5-gonal inequalities are

the

inequalities Qn(b)T d S 0,

where b is

(up

to

permutation

of

its components) one

of

the

following vectors:

b =

(1,1,1,

-1,

-1,0,

...

,0),

b

(1,1,1,

-2,

0,

...

,0),

b = (2,1,

-1,

-1,0,

...

,O),b

(3,-1,

0,

...

,0),

b = (2,1,

-2,0,

...

,0),

b

(3,

0,

...

,0).

Figure 6.1.2 shows

the

pure

4-gonal

and

5-gonal inequalities or,

rather,

their

left

hand

sides.

It

should

be

understood as follows: a

plain

edge between two

nodes

i

and

j indicates a coefficient + 1 for the variable d

ij

and

a

dotted

edge

indicates a coefficient

-1.

The

pure 5-gonal inequality is also called

the

pentagonal

inequality.

pure 4-gonal inequality

pentagonal inequality

Figure 6.1.2

6.1

Hypermetric

and

Negative

Type

Conditions

69

The

negative

type

inequalities

are classical

inequalities

in

analysis;

they

were

used,

in

particular,

by

Schoenberg

[1937, 1938a, 1938b].

The

hypermetric

in-

equalities

were

considered

by

several

authors,

including

Deza

[1960, 1962]'

Kelly

[1970a],

Baranovskii

[1971, 1973]

and,

in

the

context

of

correlations

or

boolean

quadratic

programming

(i.e.,

under

the

form

indicated

in

Lemma

6.1.14; see

also

Figure

5.2.6), by

Kelly

[1968],

Davidson

[1969], Yoseloff [1970],

McRae

and

Davidson

[1972],

Kounias

and

Marin

[1976],

Erdahl

[1987],

Mestechkin

[1987],

Pitowsky

[1991]. (Recall

Remark

5.4.11.)

The

hypermetric

inequalities:

Qn(b)T

d

::;

0 for b E

zn

with

2:7=1

b

i

=

1, define a cone

in

JR.E

n

,

called

the

hypermetric

cone

and

denoted

by

HYP

n

.

Similarly,

the

negative

type

cone

1

NEG

n

is

the

cone

in

JR.E

n

,

which

is

defined

by

the

negative

type

inequalities:

Qn(b)T

d

::;

0 for b E

zn

with

2:i'=1 b

i

=

o.

If

we

consider

an

arbitrary

finite set X

instead

of

V

n

,

then

we also

denote

the

hypermetric

cone

by

HYP(X).

In

fact,

the

negative

type

inequalities

are

implied

by

the

hypermetric

inequal-

ities.

In

other

words,

HYP

n

~

NEG

n

for all n

2:

3.

This

result

can

be

read

immediately

from

Figure

5.2.6 (by looking

at

the

corre-

sponding

inequalities

on

the

"correlation

side").

It

can

also be

derived

from

the

following

result

of

Deza

[1962]

which

shows,

more

precisely, how

(2k

+ 1)-

and

(2k

+ 2)-gonal

inequalities

relate.

Proposition

6.1.3.

Let

k

2:

1

be

an

integer.

The

(2k

+

2)-gonal

inequalities

are

implied

by

the

(2k

+

1}-gonal

inequalities.

Proof.

Let

b E

zn

with

2:i=l

b

i

= 0

and

2:i=l

Ibil

=

2k

+

2.

We show

that

the

inequality

Qn(b)T

d

::;

0

can

be

expressed as a

nonnegative

linear

combination

of

(2k

+

1)-gonal

inequalities. We

can

suppose

without

loss

of

generality

that

b

1

,

...

, b

p

> 0 > b

p

+

1

, .

..

, b

n

, for some p, 1

::;

P

::;

n -

1.

For

1

::;

i

::;

p, set

c(i)

:=

(-b

1

,

...

,

-b

i

-

1

,

1 - b

i

,

-bi+1,

...

,

-b

p

,

-b

p

+

1

,

...

,

-b

n

)

and,

for p + 1

::;

i

::;

n, set

c(i)

:=

(b

1

,

...

, b

p

,

b

p

+

1

,

...

,

bi-1,

bi

+

1,

bi+1,

...

, b

n

).

Then,

each

vector

c(i) belongs

to

zn,

has

sum

of

entries

1,

and

sum

of

absolute

values

of

its

entries

2k

+

1.

Therefore, each

inequality

Qn(c(i))T

d

::;

0 is a

(2k

+ 1)-gonal inequality. Observe now

that

L IbiIQn(c(i)) =

2kQn(b).

l:<:;i:<:;n

'We

will

consider

in

Section

31.4

another

cone

NEG

n

.

Namely, given a

graph

G = (Vn,

E),

the

cone NEG(G) is defined

as

the

projection

of

NEG

n

on

the

edge

set

on

the

subspace

JR.E

indexed

by

the

edge

set

of G.

70

Chapter

6.

Conditions

for

L1-Embeddability

This

shows

that

the

(2k + 2)-gonal

inequality

Qn(bf

d

:::;

° is

implied

by

the

(2k + 1)-gonal

inequalities

Qn(c(i)f

d

:::;

°

(1

:::;

i

:::;

n).

I

As

an

example,

the

4-gonal inequality: Q4(1,

1,

-1,

-If

d

:::;

° follows by

sum-

mation

of

the

following 3-gonal inequalities:

Q4(1,

1,

-1,

of

d:::;

0,

Q4(1,

1,0,

-If

d

:::;

0,

Q4(-1,0,1,lfd:::;0,

Q4(0,

-1,

1,

If

d

:::;

0.

Corollary

6.1.4.

The negative type inequalities are implied

by

the

hypermetric

inequalities. I

Remark

6.1.5.

Note

that

the

negative

type

inequalities do

not

imply

the

triangle

inequalities.

In

other

words, a

distance

may

be

of

negative

type

without

being

a

semimetric;

that

is,

the

negative

type

cone

NEG

n

is

not

contained

in

the

semimetric

cone

METn.

To see it, consider for

instance

the

distance

d

on

Vn

defined by

dli

= 1 for i = 2,

...

,

nand

dij = n

2

!:1

for 2

:::;

i < j

:::;

n.

Then,

d violates some

triangle

inequalities, as d

ij

- d

1j

-

dli

=

n~l

> ° for

any

i

=j=.

j E {2,

...

,

n}.

On

the

other

hand,

it

is easy

to

verify

that

d E

NEG

n

(e.g.,

because

its

image

6

(d)

-

under

the

covariance

mapping

pointed

at

position

1 - defines a positive semidefinite

matrix).

See also

Remark

6.1.11,

where

it

is

observed

that

the

k-gonal inequalities do

not

follow from

the

(k + 2)-gonal

inequalities.

On

the

other

hand,

for d E

NEG

n

,

the

condition

dln = ° implies

that

dli

= din for all i =

2,

...

, n -

1.

(Hence,

the

metric

condition

is

partially

satis-

fied.) Moreover,

letting

d'

denote

the

distance

on

the

set

Vn-l

=

Vn

\

{n}

defined

as

the

projection

of

d (i.e.,

d:

j

:=

dij for all i, j E

Vn-l),

then

d E

NEG

n

if

and

only

if

d' E

NEG

n

_

l

.

In

other

words, for

testing

membership

in

the

negative

type

cone, we

can

restrict

ourselves

to

distances

taking

only positive values.

The

same

holds

clearly for

the

hypermetric

cone. I

One

of

the

main

motivations

for

introducing

hypermetric

inequalities lies

in

the

fact

that

they

are

valid for

the

cut

cone, i.e.,

(6.1.6)

In

other

words,

Lemma

6.1.

7.

Every

distance space that is isometrically Cl-embeddable satisfies

all the hypermetric inequalities.

Proof.

It

suffices

to

verify

that

every

cut

semimetric

satisfies all

the

hypermetric

6.1

Hypermetric

and

Negative

Type

Conditions

71

inequalities. For

this,

let

S

~

Vn

and

b E

zn

with

2::7=1

b;

=

1.

Then,

is

nonpositive

since 2::;ES b

i

is

an

integer.

I

6.1.2

Hypermetric

and

Negative

Type

Distance

Spaces

Let

(X,

d)

be

a

distance

space.

Then,

(X,

d)

is

said

to

be

hypermetric (resp.

of

negative type)

if

d satisfies

all

the

hypermetric

inequalities (resp. all

the

negative

type

inequalities), i.e.,

if

d satisfies

( 6.1.8)

L

b;bjd(x;,xj)SO

l:'Oi<j:'On

for all b E

zn

with

2::7=1

b;

= 1 (resp.

with

2::7=1

bi

=

0)

and

for all

distinct

elements

Xl,

...

,

Xn

EX

(n

~

2).

Observe

that

in

the

above definition we

can

drop

the

condition

that

the

elements

Xl,

...

,X

n

be

distinct.

Indeed,

suppose

for

instance

that

Xl

=

X2.

Then,

d(Xl'

X2)

= °

and

d(Xl'

Xi)

= d(X2'

Xi)

for all i. Therefore,

the

quantity

L b;bjd(Xi, Xj)

can

be

rewritten

as L b:bjd(Xi' Xj),

after

setting

b~

=

l:'Oi<j:'On

2:'Oi<j:'On

b

l

+ b

2

,

b~

= b

3

,

...

,

b~

= b

n

.

In

other

words, (X,

d)

is

hypermetric

(resp.

of

negative

type)

if

and

only

if

d satisfies

the

inequalities

(6.1.8) for all b E

{O,

-1,

l}n

with

2::~1

b

i

= 1 (resp.

=

0)

and

all

(not

necessarily

distinct)

elements

Xl,

...

,X

n

E X

(n

~

2).

Given

an

integer k

~

1

and

f E

{O,

I},

a

distance

space (X,

d)

is

said

to

be

(2k+f)-gonal

if

d satisfies

the

inequalities (6.1.8) for

all

b E

zn

with

2::7=1

b

i

= f

and

2::7=1

Ib;1

= 2k + f

and

for all

Xl,

...

,

Xn

EX

(n

~

2).

Again

we

obtain

the

same

definition

if

we

require

that

d satisfies

all

these inequalities only for b

pure,

i.e.,

with

entries

in

{0,1,-1}.

For instance,

(X,d)

is 5-gonal

if

and

only if, for

all

Xl,X2,X3,Yl,Y2 E

X,

the

following

inequality

holds:

(6.1.9)

l:'Oi<j9

i=I,2,3

j=1,2

This

is

the

pentagonal

inequality,

that

we

rewrite

here

for

further

reference.

Observe

that

the

notion

of

k-gonal

distance

spaces is

monotone

in

k, in

the

sense

that

(k

+ 2)-gonality implies k-gonality. Namely,

Lemma

6.1.10.

Let

(X,

d)

be

a distance space.

(i)

If

(X,

d)

is (k + 2)-gonal, then

(X,

d)

is k-gonal, for any integer k

~

2.

(ii)

If

(X,d)

is (2k + 1)-gonal, then

(X,d)

is (2k + 2)-gonal, for any integer

k~1.

72

Chapter

6.

Conditions for

LI-Emheddability

Proof. (i) Suppose

that

(X,

d)

is (k + 2)-gonaL Let b E

zn

with

Ei'=l

Ib;1

= k

and

Ei'=l

bi

= E, where E = 1

if

k is

odd

and

E 0

if

k

is

even. Let

Xl,

.

..

,X

n

E

X.

We show

that

L b

i

djd(Xi,Xj):5

O.

For this, set b

l

(b,

1,

-1)

E

19<j~n

zn+2

and

Xn+l

= X

n

+2

:=

x,

where X E

X.

Then,

L

b~bjd(Xi,Xj),

which is nonpositive by

the

assumption

that

(X,d)

is

1~i<j~n+2

(k + 2)-gonaL

The

assertion (ii) follows from Proposition 6.1.3. I

Relllark

6.1.11.

Note

that

the

k-gonal inequalities do

not

follow from

the

{k + 2)-gonal inequalities (k

2::

2). (The proof of

Lemma

6.1.10 (i) works indeed

at

the

level of distance spaces since

we

make

the

assumption

that

the

two points

Xn+l

and

Xn+2

of X coincide.). For instance,

the

5-gonal inequalities do

not

imply

the

triangle inequalities. To see it, consider

the

distance d on

V5

defined

by

d;j = 1 for all pairs except d

1

2

f!

and

d34

~.

Then,

d violates some

triangle inequality as

d12

d13

d23

t >

OJ

on

the

other

hand, one can verify

that

d satisfies all 5-gonal inequalities. I

Relllark

6.1.12.

Equality

case

in

the

hyperllletric

and

uegative

type

inequal-

ities.

The

following question is considered by Kelly [1970a], Assouad

[1984J,

Ball

[1990J.

What

are

the

distance spaces, within a given class,

that

satisfy a given hypermetric

or

negative

type

inequality

at

equality?

For instance, Kelly [1970a] characterizes

the

finite subspaces

of

(lK,

d

l1

)

that

satisfy

the

(2k + I )-gonal inequality

at

equality. Namely, given

Xl

•...

,

Xk+I,

YI,

...

,

Yk

E

lK,

the

equality

l~i<jS;k

l~iSk+l

1$;$'"

holds if

and

only if

Yl,."

,

Yk

separate

Xl,

...

,

Xk+b

i.e., if there exist a

permutation

a

of

{I,

...

, k + I}

and

a

permutation

(3

of

{I,

...

,

k}

such

that

xa(l)

::;

Yf3(l)

::;

Xa(2)

::; Yf3(2) ::;

.•.

::; Yf3(k) ::;

Xa(k+l)'

This

can

be easily verified by looking

at

the

explicit decomposition

of

the

distance space

({

XI,

••.

,

Xk+1,

Yl>

...

,

Yk},

d

c

,)

as a nonnegative

sum

of

cuts

(and

using

the

construction

from

the

proof

of

Proposition

4.2.2

(ii)

==}

(i)). Generalizations

and

Deza M.M., Laurent M. Geometry of Cuts and Metrics

Подождите немного. Документ загружается.