Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.

6.3 A
Chain
of
Implications
(i) (X,
d)
is
L2
-embeddable.
(ii) (X,
d)
is
Ll
-embeddable.
(iii) (X,
d)
is hypermetric.
(iv) (X,
d)
is
of
negative type.
(v) (X,
Vd)
is L
2
-embeddable.
(vi) D has exactly one positive eigenvalue.
83
We have the chain
of
implications: (i)
==*
(ii)
==*
(iii)
==*
(iv)
~
(v)
==*
(vi) .
Proof.
The
implication
(i)
==*
(ii) is a classical
result
in
analysis; see
Propo-
sition
6.4.12 below for a proof.
The
implication
(ii)
==*
(iii) follows from
Lemma
6.1.7,
and
(iii)
==*
(iv) from
Corollary
6.1.4. Finally, (iv)
~
(v)
holds
by
Theorem
6.2.2
and
(iv)
==*
(vi)
by
Theorem
6.2.16. I
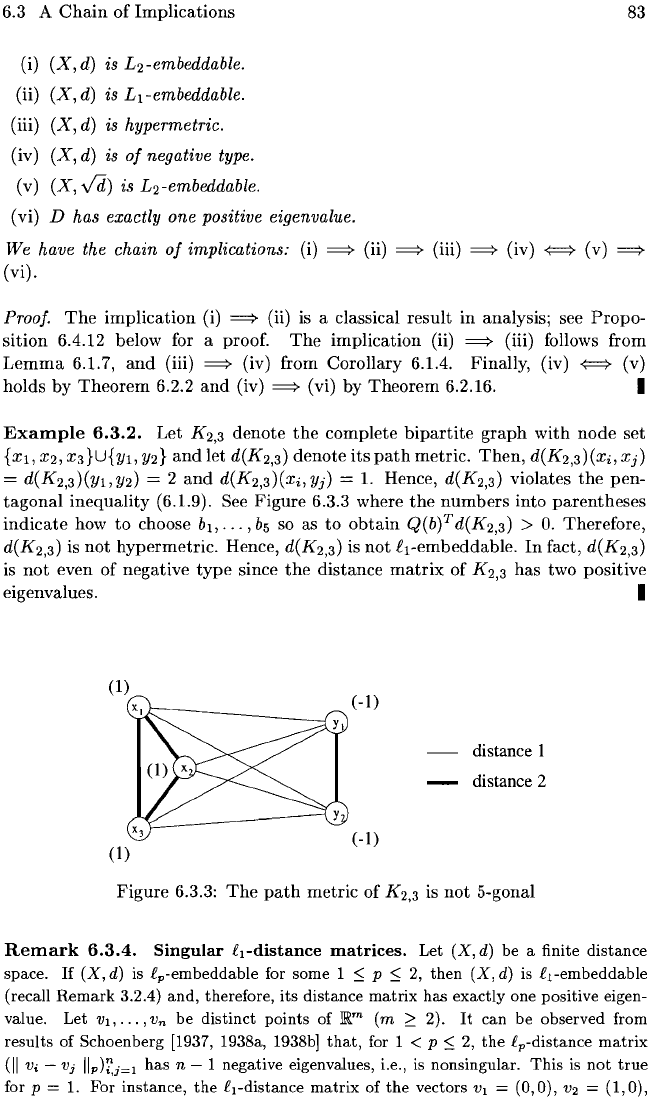
Example
6.3.2.
Let
K
2
,3
denote
the
complete
bipartite
graph
with
node
set
{Xl,
X2,
X3}U{Yl,
Y2}
and
let
d(K
2
,3)
denote
its
path
metric.
Then,
d(K2,3)(Xi, Xj)
=
d(K
2
,3)(Yl,Y2)
= 2
and
d(K
2
,3)(Xi,Yj)
=
1.
Hence,
d(K
2
,3)
violates
the
pen-
tagonal
inequality
(6.1.9). See
Figure
6.3.3 where
the
numbers
into
parentheses
indicate
how
to
choose b!,
...
,
b5
so as
to
obtain
Q(b)T
d(K
2
,3)
>
o.
Therefore,
d(K
2
,3)
is
not
hypermetric.
Hence, d(K2,3) is
not
el-embeddable.
In
fact, d(K2,3)
is
not
even
of
negative
type
since
the
distance
matrix
of
K
2
,3
has
two
positive
eigenvalues. I
(1)
(1)
(
-1)
(-I)
distance I
distance 2
Figure
6.3.3:
The
path
metric
of
K
2
,3
is
not
5-gonal
Remark
6.3.4.
Singular
ii-distance
matrices.
Let (X,
d)
be
a finite distance
space.
If
(X,
d)
is
ip-embeddable
for
some 1
::;
p
::;
2,
then (X,
d)
is
irembeddable
(recall Remark 3.2.4) and, therefore, its distance matrix has exactly one positive eigen-
value. Let
VI,
..•
,
Vn
be distinct points of
lPI.
m
(m
~
2).
It
can be observed from
results of Schoenberg
[1937,
1938a,
1938bJ
that,
for
1 < p ::;
2,
the ip-distance matrix
(II
Vi
-
Vj
IIp)~j=1
has n - 1 negative eigenvalues, i.e.,
is
nonsingular. This
is
not true
for
p = 1. For instance, the ii-distance matrix of the vectors
VI
= (0,0),
V2
= (1,0),

84
Chapter
6.
Conditions for L1-Embeddability
V3
(0,1)
and 1)4
(1,1),
is singular. Several characterizations have been given for
the
configurations
of
distinct points
VI,
•••
,
Vn
E
IRm
(m
~
2) whose
iI-distance
matrix
(II
Vi
Vj
lid
is
nonsingular Reid
and
Sun [1993]; see also Lin
and
Pinkus
[1993]
for applications
to
ridge functions interpolation). In particular, let A =
(aij)
denote
the
n X n
matrix
whose
entry
aij
is
defined as
the
number
of
positions where
the
coordinates
of
the
vectors
Vi
and
Vj
coincide m -
aii
is
equal
to
the
Hamming
distance between
Vi
and
Vj).
The
matrix
A is positive semidefinite. Moreover, A is positive definite if
and
only
if
the
matrix
(II
Vi
-
Vj
is nonsingular. I
The
implication (ii)
==;..
(iii) of Theorem 6.3.1 is, in general,
strict
(as was
first observed by Assouad
[1977]
and
Avis [1981]).
It
is strict
5
,
in particular,
if
7
~
IXI
<
00.
In
other
words,
the
inclusion CUTn
<;
HYP
n
is strict for n
~
7.
To see it,
it
suffices
to
exhibit
an
inequality which defines a facet for
CUT
nand
is
not
hypermetric. Many such inequalities are described in
Part
V.
However, there are many examples of classes
of
distance spaces
(X,
d)
for
which
the
properties of being hypermetric
and
L1-embeddable are equivalent.
Such examples
with
X infinite will
be
presented in
Chapter
8.
We summarize
below what
is
known
about
this question.
Remark
6.3.5.
We give here a list
of
distance spaces
(X,
d)
for which L
1
-
embeddability
can
be
characterized by a set T of inequalities
that
are
all hyper-
metric or
of
negative type.
(i)
(Vn,
d)
with
n
~
6;
T consists
of
the
hypermetric inequalities, i.e., CUTn =
HYP
n for n
~
6 (see Section 30.6). More precisely, T consists
of
the
p-gonal
inequalities
with
p =
3,5
in
the case n =
5,
and
p
3,5,7
in
the
case n
6.
(ii) A normed space
(IR
m
,
d
ll
.
II
); T consists
of
the
negative
type
inequalities (see
Theorem
8.3.1).
(iii) A normed space
(IRm,
dll.lI)
whose
unit
ball is a polytope; T consists of
the
7-gonal inequalities (see Theorem 8.3.2).
(iv)
(L,
d,;)
where (L,:5) is a poset lattice, v is a positive valuation on L,
and
d1J(x,
y) vex Vy)
vex
1\ y) for x, y E
Lj
T consists of
the
5-gonal inequalities
or, equivalently,
T consists
of
the
negative
type
inequalities (see Theorem 8.1.3
and
Example 8.2.6).
(v)
(A,
d)
where A
is
a family of subsets
of
a set n which is stable under
the
symmetric difference, v is a nonnegative function on A such
that
v(0) = 0,
and
d(.A,
B)
:=
v(A6B)
for
A,
B E
Ai
T consists of
the
inequalities of negative
type
(see Corollary 8.2.8).
5This
implication
remains
strict
in
the
case X = N. For this, consider for
instance
the
distance
d
on
N
obtained
by
taking
iterative
spherical t-extensions (see Section 7.3) of
the
path
metric
of
the
SchHifli
graph
GZ7. Hence, dij is
the
shortest
length
of a
path
joining i
and
j
in G
Z
7
if i
and
j are
both
nodes of
GZ
7
and d
ij
= t otherwise. For t
~
!,
dis
hypermetric
(by
Proposition
14.4.6),
but
d is
not
Lt-embeddable
{since
the
path
metric
of
GZ7
lies
on
an
extreme
ray of
the
hypermetric
cone
on
27 points; see Section 16.2}.

6.3 A
Chain
of
Implications
85
(vi)
The
graphic space (V,d(G)) where G is a connected bipartite graph
with
node set V; I consists of the 5-gonal inequalities (see Theorem 19.2.1).
(vii)
The
graphic space
(V,
d(
G)) where G
is
a connected graph on
at
least 37
nodes
and
having a node adjacent to all other nodes; I consists of the negative
type
inequalities
and
the
5-gonal inequalities (see Corollary 17.1.10 (i)).
(viii)
The
graphic space (V,d(G)) where G is a connected
graph
on
at
least
28
nodes
and
having a node adjacent
to
all other nodes; I consists
of
the hyperrne-
tric inequalities (see Corollary 17.1.10 (ii)).
I
We
conclude
with
mentioning two examples
of
application of negative type
inequalities to geometric questions, taken from Deza
and
Maehara
[1994].
The
first one concerns
the
following theorem
of
Rankin
[1955]
(related to the problem
of determining the maximum number of disjoint balls
that
can
be packed
in
a
given ball).
Theorem
6.3.6.
Let R <
~
and let N R denote the
maximum
number N
of
points
Xl,
...
, X N that can
be
placed in a closed (Euclidean) ball
of
radius R
in such a way that
II
Xi-Xj
11221
for
alii
i=
j =
1,
...
,N.
Then,
NR
Proof. A short
proof
can
be given using negative type inequalities. Suppose
Xl,
..•
, X N lie in the ball of center
Xo
and
radius R
and
that
II
Xi
-
Xj
1 for all
i
i=
j
1,
...
,
N.
Applying
the
negative type inequality Q(
-n,
1,
...
,1)T X
S.
0
to
the
distance d on {XO,Xl,
...
,XN}
defined by d(Xi,Xj)
:=
(II
Xi
-
Xj
112)2
for
all
i,j,
we
obtain
the inequalit,y:
As
d(xo,
Xi)
that
is, N
N
N:Ed(xo,Xi)
2
:E
d(x;,xj).
i=l
l:<:;i<j:<:;N
R2
and d(X;, Xj) 2 1
for
i
i=
j
s.
n this implies
that
N
2
R2
2
(~);
NR L
l
_;R2J.
Equality is
attained
by considering for
Xl,
..•
,XIV
vertices of a regular
(N
- 1}-dimensional simplex with side length
Xi·
I
The
next result concerns a generalization of the well-known parallelogram
theorem to higher dimensions. This theorem asserts
that,
given four distinct
points
Xl,
X2,
Yl,
Y2,
the following inequality holds:
(II
Xl
-
YI
112)2
+
(II
Xl
2
(II
Xl
Y2
112)2
+
(II
X2
X2
Ib?
+
(II
YI
Yl
112)2
+
(II
X2
-
Y2
112)2
Y2112?
with
equality
if
and
only if
XIYlX2Y2
is a parallelogram.
Given a polytope
P,
a line segment joining two vertices of P
is
called a
diagonal of P if
it
is not contained in any proper
face
of P. An n-parallelotope
is
the
vector
sum
of n segments with a common endpoint such
that
no segment
is contained in
the
affine hull of the others (thus, a parallelogram if n = 2).

86
Chapter
6.
Conditions for
Ll-Embeddability
Theorem
6.3.7.
Let
P
be
a polytope
in
lPl.
n
that is combinatorially equivalent to
an
n-dimensional
hypercube, let
G(P)
:=
(Vp,
Ep)
denote its
I-skeleton
graph,
and
let
Dp
denote
the
set
of
diagonals
of
P.
Then,
xyEEp
xyEDp
with
equality
if
and
only
if
P is
an
n-parallelotope.
Proof.
The
proof
is by
induction
on
n.
It
relies essentially on
the
following
identity:
n
L
(II
Xi
-
Yj
112)2
- L
(II
Xi
-
xi'
112)2
+
(II
Yi
- Yi'
112)2
= n
2
(11
p - q
112)2
i,j=l
for any
points
Xl,
...
,X
n
,
Yl,··
.
,Yn
and
setting
p
:=
~
L~l
Xi,
q
:=
~
L~l
Yi·
See Deza
and
Maehara
[1994]
for details. I
6.4
An
Example:
The
Spherical
Distance
Space
We describe here a classical example of
1\
-embeddable distance space, namely,
the
spherical distance space.
This
is
the
distance space defined
on
a sphere
S,
taking
as distance between two
points
x,
yES
the
quantity
(6.4.1)
(
(X
- c)T(x -
Y))
r . arccos r2 '
where
c denotes
the
center of
Sand
r
its
radius.
The
quantity
(6.4.1) is known
as
the
spherical distance (or great circle metric) between X
and
y. (This is
the
geodesic distance
on
the
sphere S between
the
points
X
and
y,
which coincides
with
the
angle between
the
two vectors from c
to
X
and
from c
to
y.) We
may
clearly suppose
that
the
sphere S is centered
at
the
origin
and,
up
to
scaling
of
the
distances,
that
it
has
radius
1. Let Sm denote
the
m-dimensional
unit
sphere, i.e.,
m+l
Sm
:=
{x
E
lPl.
m
+
l
I L
x~
=
I}.
i=l
We let
Sm
denote
the
distance space
(Sm,ds),
where
ds
is
the
distance
defined
by (6.4.1), i.e.,
( 6.4.2)
ds(x,y):=
arccos(xTy) for all
X,y
E Sm.
Similarly,
we
let Sm,r denote
the
distance space
(Sm,ndS),
where Sm,r is
the
m-dimensional
sphere centered
at
the
origin
with
radius
rand
ds
is defined by
(6.4.1). So,
Sm
=
Sm,l.
The
distance space Sm,r is called a spherical distance
space.
We refer
to
Blumenthal
[1953]
for a detailed
study
ofthe
metric
properties
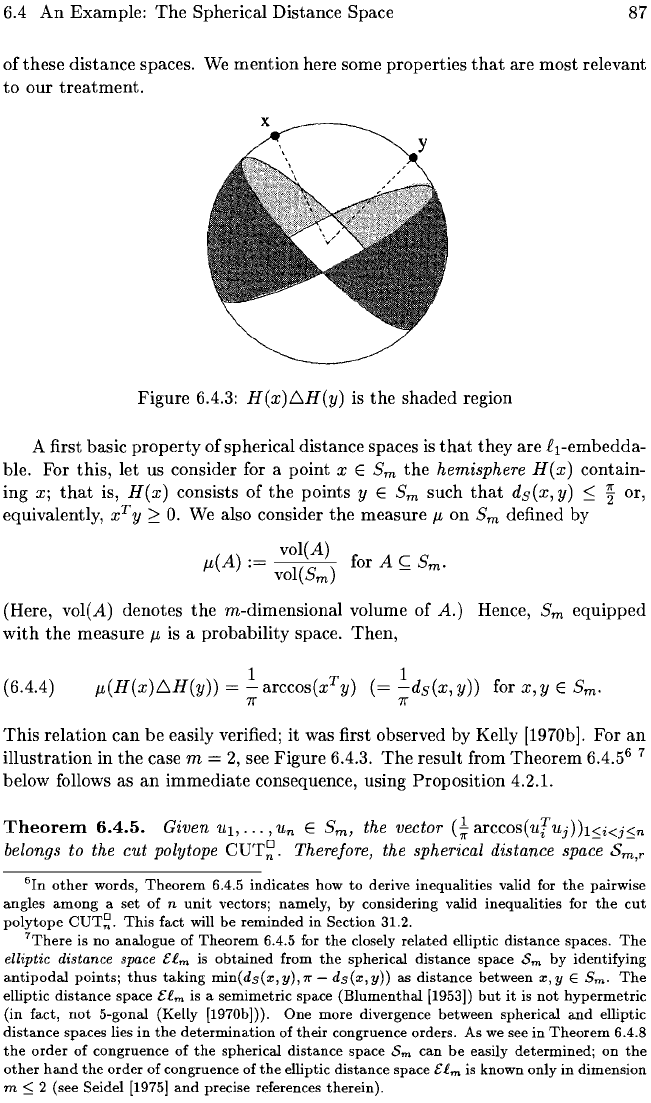
6.4
An
Example:
The
Spherical Distance Space
87
of
these
distance
spaces.
We
mention here some
properties
that
are
most
relevant
to
our
treatment.
x
Figure 6.4.3: H(x)f::,H(y) is
the
shaded
region
A first basic
property
of
spherical distance spaces
is
that
they
are fll-embedda-
ble. For this, let us consider for a
point
x E
Sm
the
hemisphere
H(x)
contain-
ing
x;
that
is,
H(x)
consists of
the
points
y E
Sm
such
that
ds(x,y)
S I or,
equivalently,
x
T
y
2:
O.
We also consider
the
measure
J-L
on
Sm
defined by
II(A) '.= vol(A) £
,..
or A
<;;;
Sm.
vol(Sm)
(Here,
vol(A) denotes
the
m-dimensional volume
of
A.) Hence,
Sm
equipped
with
the
measure
J-L
is
a probability space.
Then,
(6.4.4 )
1 1
J-L(H(x)f::,H(y)) =
-arccos(xTy)
(=
-ds(x,y))
for
x,y
E Sm.
7r 7r
This
relation
can
be
easily verified; it was first observed by Kelly [1970bj. For
an
illustration
in
the
case m =
2,
see
Figure
6.4.3.
The
result from
Theorem
6.4.5
67
below follows as
an
immediate
consequence, using
Proposition
4.2.1.
Theorem
6.4.5.
Given Ul,
...
,
Un
E Sm, the vector
(~arccos(uT
Uj)h:Si<j:Sn
belongs to the cut polytope
CUT~.
Therefore, the spherical distance space Sm,r
6In
other
words,
Theorem
6.4.5
indicates
how
to
derive
inequalities
valid for
the
pairwise
angles
among
a
set
of
n
unit
vectors; namely,
by
considering
valid
inequalities
for
the
cut
polytope
CUT~.
This
fact
will
be
reminded
in
Section
3l.2.
7There
is
no
analogue
of
Theorem
6.4.5 for
the
closely
related
elliptic
distance
spaces.
The
elliptic distance space
elm
is
obtained
from
the
spherical
distance
space 8
m
by
identifying
antipodal
points;
thus
taking
min(ds(x,
y),
7l"
-
ds(x,
y))
as
distance
between
x,
y E Sm.
The
elliptic
distance
space
elm
is a
semimetric
space
(Blumenthal
[1953])
but
it
is
not
hypermetric
(in
fact,
not
5-gonal (Kelly [1970b])).
One
more
divergence
between
spherical
and
elliptic
distance
spaces
lies
in
the
determination
of
their
congruence
orders. As we see
in
Theorem
6.4.8
the
order
of
congruence
of
the
spherical
distance
space 8
m
can
be
easily
determined;
on
the
other
hand
the
order
of
congruence
of
the
elliptic
distance
space
elm
is
known
only
in
dimension
m
:S
2 (see Seidel [1975]
and
precise references
therein).

88
Chapter
6.
Conditions
for L
1
-Embeddability
is
isometrically
£1
-embeddable for every r > 0, m
2':
1.
I
In
fact,
isometric
subspaces
of
spherical
distance
spaces
and
of
Euclidean
distance
spaces
are
very closely
related
notions, as
the
results
below
indicate.
Let
d
be
a
distance
on
the
set
Vn
:=
{I,
...
,
n}.
Consider
the
symmetric
matrix
8
A = (aij )f,j=l defined by
aij
:=
cos (dij ) for i, j = 1,
...
,n.
Hence,
the
diagonal
entries
of
A
are
all
equal
to
1.
Moreover, let d
denote
the
distance
on
the
set
Vn
U
{xo}
(xo is a new element
not
belonging
to
V
n
) defined
by
d(xo, i) = 1
d(i,j)
= 2 -
2cos(d(i,j))
=
4sin2(d(~j))
for i E V
n
,
for
i,j
E V
n
.
Proposition
6.4.6.
Let
m
2':
1
be
an
integer
and
d,
d,
and
A
be
defined as
above.
The
following assertions are equivalent.
(i)
The distance space (Vn,
d)
is
an
isometric
subspace
of
the
m-dimensional
spherical distance space Sm.
(ii) dij E
[0,7r]
for
all i, j E
Vn
and
the
matrix
A is positive
semidefinite
with
rank
A
:S
m + 1.
(iii) dij E
[0,7r]
for
all i, j E
Vn
and
the distance space (Vn U
{xo},
d) can
be
isometrically
embedded
into
£2'+1.
Proof.
The
equivalence (i)
~
(ii) is clear. Indeed, (Vn, d) is
an
isometric
subspace
of
Sm
if
and
only
ifthere
exist
U1,
.
..
,Un E Sm
such
that
cos(d(i,
j))
=
ut
Uj
for all
i,j
E V
n
;
that
is,
if
the
matrix
A
is
positive semidefinite
with
rank
:S
m + 1.
The
equivalence
(ii)
~
(iii) follows from
Corollary
6.2.5
and
the
fact
that
A coincides
with
the
matrix
Pxo(Vn U
{xo},d).
I
Corollary
6.4.7.
A distance space (Vn,
d)
embeds isometrically
in
Sm,r (for
some
m
2':
1)
if
and
only
if
d
ij
E
[O,7rr]
for all
i,j
E
Vn
and
the
matrix
A
:=
(cos(
~
) )i,j=l is positive semidefinite. Then, the
smallest
m such
that
(Vn' d) embeds
into
Sm,r is m =
rank
A -
1.
I
Using
Proposition
6.4.6, one
can
derive a
compactness
result
for
spherical
distance
spaces analogue
to
the
compactness
result for
Euclidean
spaces from
Theorem
6.2.13;
this
result
can
be
found
in
Blumenthal
[1953].
Theorem
6.4.8.
Given m
2':
1, a distance space
(X,
d)
can
be
isometrically
embedded
into
the
m-dimensional
spherical distance space Sm
if
and
only
if
the
8We
will
study
in
detail
in
Section
31.3
the
set
of
positive
semidefinite
matrices
with
all
diagonal
entries
equal
to
1.
We
will use,
in
particular,
Theorem
6.4.5.

6.4
An
Example:
The
Spherical
Distance
Space 89
same holds for every subspace (Y,
d)
where Y
~
X with
IYI
= m + 3. I
In
particular,
the
order
of
congruence
of
the
spherical
distance
space Sm is
equal
to
m + 3. To see
it,
consider
the
distance
space (X,
d),
where
IXI
2 m + 3
and
dij
:=
arccos ( -
m~l)
for all i
-I-
j E
X.
Then,
(X,
d)
does
not
embed
in
Sm
(because
the
matrix
(cos( d
ij
)
)i,jEX
is
not
positive semidefinite).
On
the
other
hand,
every
subspace
(Y,d)
with
IYI
= m + 2
embeds
in
Sm (as
(COS(dij))i,jEY
is
positive
semidefinite
with
rank
m + 1).
There
are
further
intimate
links between
the
spherical
and
Euclidean
dis-
tances.
In
fact, as Schoenberg [1935] observed, every
set
of
affinely
independent
vectors
equipped
with
the
Euclidean
distance
can
be isometrically
embedded
into
some
spherical
distance
space.
And,
if
the
vectors are
not
independent,
their
Euclidean
distances
can
be realized
asymptotically
as
limits
of
spherical
distances.
This
permits
to
derive
the
well-known implication:
"1:
2
-embeddable
===}
1:
I-embeddable"
.
Proposition
6.4.9.
Let
Uo,
UI,
...
,Un
E
lIR
n
be
affinely independent. Then, the
distance space
({
Uo,
UI,.'"
un},
dl
2
)
is
an isometric subspace
of
Sn,T
for some r
large enough.
Proof. We
can
suppose
without
loss
of
generality
that
Uo
:=
O.
By
assumption,
the
matrix
P =
(Pij
:=
u[
Uj
)~j=1
is positive definite.
Let
A(r)
be
the
(n + 1) x
(n + 1)
symmetric
matrix
with
entries aij
:=
cos
(~)
for i, j =
0,
1,
...
,
n.
In
view
of
Corollary
6.4.7,
it
suffices
to
show
that
A(r)
>-
0 for r large enough.
In
what
follows,
we
write
A
'"
B for two
matrices
A
and
B
if
A
>-
0
¢=}
B
>-
O.
Clearly,
A(r)
'"
B(r),
where
the
OO-th
entry
of
B(r)
is
boo
:=
1,
its
Oi-th
entry
is
b
Oi
:=
aOi
- 1 (for i =
1,
...
,n)
and
its
ij-th
entry
is b
ij
:=
aij -
aOi
-
aOj
+ 1 (for
i,
j = 1,
...
, n)
(to
see it,
subtract
the
row
indexed
by 0
in
A( r)
to
every
other
rowand,
then,
the
column
indexed
by 0
to
every
other
column).
We now use
the
fact
that
cosx
= 1 -
!x
2
+
0(x
4
)
when
x
-----+
O.
Hence, each
entry
of
B(r)
can
be
expressed
as
bOi
= -
~
Pii
+
o(;:\-
),
bij
= h Pij +
o(;:\-
).
Therefore,
after
suitably
scaling
B(r),
we
obtain
that
A(r)
'"
B(r)
'"
C(r),
where
the
O-th
entry
of
C(r)
is 4r2,
its
Oi-th
entry
is
Pii
+ o(
h),
and
its
ij-th
entry
is Pij +
o(h).
One
can
now easily verify
that
C(r)
>-
0 for any r large enough. (Note here
that
it
suffices
to
check
that
the
n+ 1
principal
subdeterminants
of
C(r)
disposed along
the
diagonal
are positive, which holds for r large
enough
by
the
assumption
that
P>-
0.)
I
Remark
6.4.10.
Proposition
6.4.9
extends
to
an
arbitrary
set
of
vectors
in
the
case
when
they
all lie
on
a
common
line.
But,
it
does
not
extend
to
an
arbitrary
set
of
vectors
in
dimension
2
2.
As
counterexample,
take
for
UI,
...
,Un+1
the
vertices
of
an
equilateral
simplex
and
for
Uo
the
barycentrum
of
the
simplex.
Then,
the
distance
space ({
Uo,
UI,
...
,un+d,
dl
2
)
does
not
embed
in
any spheri-
cal
distance
space. I

90
Chapter
6.
Conditions for L1-Embeddability
Let us now
indicate
how
the
Euclidean distance
can
be
approximated
by spherical
distances
9
•
For this, let
UI,
...
,Un
E Rm. We are interested
in
evaluating
their
mutual
Euclidean
distances. So, set dij
:=11
Ui
-
Uj
112
for i, j = 1,
...
,n.
We
show how to express
d as a limit
of
distances
d(r)
(when r
---+
(0) where each
d(r)
can
be
isometrically
embedded
in
Sm,r.
The
idea for
this
is intuitively very
simple. Namely, for r
> 0 consider
the
sphere s(r)
in
the
space R
m
+
1
with
center
C
:=
(0,
...
,0,
r)
and
radius
r.
One
can
visualize s(r) as a sphere lying on
top
of
R
m
,
being
viewed as
the
hyperplane
Xm+1
= 0
in
Rm+l.
Every vector U E R
m
with
II
U
112::::
r
can
be
'lifted' to a
point
u(r)
E s(r), by
setting
Let r
:::::
max?=l
II
Ui
112.
For i =
1,
...
,n,
let
u~r)
E s(r) be
the
'lifting'
of
Ui
as
defined above. Set
( )
((U.
-
c)T(u·
-
C))
dr(i,j):=r·arccos
' r2 J
fori,j=I,
...
,n.
So,
d(r)(i,j)
represents
the
spherical distance between u)r)
and
u;r)
on
the
sphere
s(
r). Clearly,
this
length
converges to
the
Euclidean distance
II
Ui
-
Uj
112
as r
tends
to
infinity, i.e.,
(6.4.11)
lim
d(r)(i,j)
=11
Ui
-
Uj
112.
r---->oo
In
a precise way, one
can
estimate
d(
r)
(i,
j)
for large r as follows:
d(
r)
(.
.)
(V
r2
-(lI
u
i
112)2y'r
2
-(lIuj
112)2+U;
Uj
)
~,J
= r . arccos
r2
= r . arccos (
VI
-
(llu;~2)2
VI
_
(1Iu;~2)2
+
Uf;j)
~
r . arccos (1 -
(IIUi;~dI12)2)
~II
Ui
-
Uj
112
.
(Here,
we
use
the
fact
that
JI=X
~
1 -
!x
and
arccos(1 - x2)
~
V2x
as
x
---+
0.) I
Proposition
6.4.12.
For a distance space
(X,
d),
d is isometrically l2-embeddable
==}
d is isometrically ll-embeddable.
Proof.
This
follows from
the
above observations, (6.4.11)
and
Theorem
6.4.5. I
9This
fact
was
already
observed
in
Kelly
[1975].

6.4
An
Example:
The
Spherical Distance Space
91
6.5
An
Example:
Kalmanson
Distances
We mention here
another
class
of
el-embeddable semimetrics arising from
the
so-called
Kalmanson
distances. These distances present moreover
the
interest-
ing feature
that
they
yield polynomial-time solvable instances of
the
traveling
salesman problem.
Let
d
be
a distance
on
the
set
Vn
{I,
...
,
n}.
We say
that
d is a K
almanson
distance
if
it
satisfies
the
condition:
for all
1
SiS
j S r S s S n.
In
this definition,
the
ordering of
the
elements
is
important;
so
we
also say
that
d
is
a Kalmanson distance
with
respect
to
the
ordering
1,
...
,n.
Moreover, it is convenient
to
visualize
the
elements 1,
...
,n
as
being ordered along a circuit in
that
circular order. For 1 S i < j S
n,
set
(the
indices being
taken
modulo n)
and
[i,j]
:=
{i,i
+
1,
...
,j
-I,j}.
Chepoi
and
Fichet [1996] observed
the
following fact.
Lemma
6.5.1.
Every
distance d
on
Vn
can
be
decomposed as
2d
= L
O!;j(d)
8([i +
l,j]).
l$i<j$n
Proof.
It
is a simple verification.
I
We introduce one more definition. A distance d on
Vn
is
said
to
be
circular
decomposable
if
d can
be
decomposed as
d = L
O!ij8([i
+
I,
j])
l$i<j$n
for some nonnegative scalars
O!ij
(1
S i < j S
n);
hence, it is el-embeddable.
As
all O!;j(d)'s are nonnegative
if
d is a Kalmanson distance,
we
deduce from
Lemma
6.5.1
that
every Kalmanson distance is circular decomposable.
It
can
be
easily
verified
that,
conversely, every circular decomposable distance is a Kalmanson
distance. Therefore,
we
have
the
following resultlO.
Proposition
6.5.2.
A distance d
is
a
Kalmanson
distance
if
and
only
if
it
is
circular decomposable (with respect to the
same
ordering). I
ExaIllple
6.5.3.
Here are some examples of Kalmanson distances.
First,
the
path
metric
of
a weighted tree is a Kalmanson distance for some ordering of
equivalence between Kalmanson distances
and
circular decomposable distances was
proved
earlier
by
Christopher,
Farach
and
Trick [1996];
their
proof
is, however,
more
compli-
cated
than
the
one
presented
here,
due
to
Chepoi
and
Fichet
[1996].

92
Chapter
6.
Conditions
for
LI-Embeddability
the
nodes
of
the
tree
(Bandelt
and
Dress [1992]). As
another
example,
consider
a
set
of
points
X
:=
{Xl,
...
,
xn}
in
the
plane
]F.2
such
that
the
xi's
lie
on
the
boundary
of
their
convex
hull
and
occur
in
that
circular
order
along
the
boundary.
Then,
the
set
X
equipped
with
the
Euclidean
distance
ll
df2
provides
a
Kalmanson
distance
with
respect
to
the
given
ordering
(Kalmanson
[1975]).
To see
it,
consider
four
points
Xi,
Xj,
X"
Xs
occurring
in
that
order
along
the
boundary.
Then,
the
segments
[Xi,
x
r
]
and
[Xj,
xs]
intersect
in
a
point
y.
We
obtain
that
df2
(Xi, X
j)
+
df2
(X"
X
s)
:S
df2
(Xi, y) + d
f2
(y, X
j)
+ d
f2
(X"
y)
+
df2
(y, X
s)
=
df2
(Xi, X
r
) +
df2
(Xj,
Xs).
I
From
a
computational
point
of
view, Deineko,
Rudolf
and
Woeginger [1995]
show
that
one
can
test
whether
a
distance
on
n
points
is a
Kalmanson
distance
with
respect
to
some
ordering
of
the
elements
and
find
such
an
ordering
in
time
O(n
2
log n). We conclude
with
mentioning
an
application
to
the
traveling
salesman
problem.
Remark
6.5.4.
An
application
to
the
traveling
salesman
problem.
The
traveling
salesman
problem
12
can
be
formulated
as follows. Given a
distance
d
on
V
n
,
find a
Hamiltonian
circuit (i
l
,
...
,
in)
whose weight:
n-l
L
d(ih'
ih+l)
+
d(in'
i1)
h=l
is
mmlmum.
This
is
an
NP-hard
problem.
The
problem
remains
NP-hard
for
Euclidean
distances
(that
is,
if
d
represents
Euclidean
distances
among
a
set
of
points
in
some
space ]F.m)
and,
thus,
for fi1-distances. However, as was
already
observed
by
Kalmanson
[1975]'
the
traveling
salesman
problem
can
be
solved
very
easily for
Kalmanson
distances.
Indeed,
suppose
that
d is a
Kalmanson
distance
on
Vn
with
respect
to
the
ordering
1,
...
,n.
Then,
the
Hamiltonian
circuit
(1,
...
, n)
has
minimum
weight.
Indeed,
from
Lemma
6.5.1,
we
obtain
that
the
weight
of
the
circuit
(1,
...
, n) is
equal
to
2:1<i<j<n Qij(d).
On
the
other
hand,
the
quantity:
2:
1
:S
i
<j:Sn
Qij
(d)
is a lower
bound-
for
the
weight
of
any
Hamiltonian
circuit
(since a
circuit
and
a
cut
meet
in
at
least two edges). I
11The
same
holds
if
we
consider
an
arbitrary
norm
metric
on
]F.2
instead
of
the
Euclidean
distance
or,
more
generally, a
projective
metric
(to
be
defined
later).
12The
reader
may
consult
Lawler,
Lenstra,
Rinnoy
Kan
and
Shmoys
[1985] for
detailed
in-
formation
on
this
problem.
