Deza M.M., Laurent M. Geometry of Cuts and Metrics

M.M. Deza, M. Laurent, Geometry of Cuts and Metrics, Algorithms and Combinatorics 15,

DOI 10.1007/978-3-642-04295-9_7, © Springer-Verlag Berlin Heidelberg 2010

Chapter

7.

Operations

We describe here several operations which

permit

to

extend

a given distance

on

Vn

to

a distance on V

n

+

1

•

Examples of such operations include

the

gate

extension operation,

the

antipodal

extension operation,

the

spherical extension

operation,

which are described, respectively, in Sections 7.1, 7.2

and

7.3.

We

also consider

the

direct

product,

the

tensor

product,

and

the

I-sum

operations

in

Sections 7.5

and

7.6.

We

discuss, in particular, conditions

under

which these

operations

preserve

metric

properties such as

fi

1

-

or

hypercube embeddability,

the

hypermetric

and

negative

type

conditions, or membership

in

the

cut

lattice.

The

cut

lattice

Ln

is defined by

Ln

:=

{l:

>'so(S)

I

>'s

E Z for all S}.

s

More

information

on

Ln

will be given

in

Section 25.1.

In

Section 7.4,

we

treat

in

detail

the

example

of

the

cocktail-party graph.

This

graph

plays,

in

fact, a cen-

tral

role

in

the

theory

of

fi1-embeddings. Indeed,

it

is one

of

the

possible factors

(besides

the

half-cube

graph

and

the

Gosset graph)

that

may

enter

the

canoni-

cal

metric

representation

of

a hypermetric or

fi

1

-graph

(see Theorems 14.3.6

and

14.3.7).

The

specificity

of

the

cocktail-party

graph

is also

demonstrated

by

the

following result

of

Cameron, Goethals, Seidel

and

Shult [1976]:

The

only con-

nected regular

graphs

on n >

28

nodes whose adjacency

matrix

has

minimum

eigenvalue 2

-2

are line graphs

and

cocktail-party graphs.

7.1

The

Gate

Extension

Operation

Let d

be

a distance on

Vn

=

{I,

...

,n}

and

let a ERr.

We

define a distance d'

on

V

n

+

1

=

Vn

U {n + I} by

setting

(7.1.1)

{

d'(I,n

+ 1) =

a,

d'(i,n+I)

=a+d(I,i)

d'(i,j)

=

d(i,j)

for 2::; i

::;

n,

for 1

::;

i < j

::;

n.

The

distance d'

is

called a gate extension

of

d

and

is

denoted

by gat",(d).

This

operation

will

be

used especially

in

the

case a =

OJ

then, gato(d)

is

also called

the

gate

a-extension

(or, simply, a-extension)

of

d.

By construction, gat",(d) satisfies

the

following triangle equalities:

d'(i, n

+ 1) =

d'(I,

n + 1) +

d'(I,

i)

94

Chapter

7.

Operations

for all i =

2,

...

, n.

From

this

follows

immediately

that

any

lllr-realization

of

gat",(d) is necessarily

of

the

form

gat",(d)=

L

>'s8(S)+0:8({n+1}),

S<;;Vn,l\tS

where

d = 2:S<;;V

n

,l\tS

>'s8(S).

The

can

be

easily checked.

Proposition

7.1.2.

Let

d

be

a distance

on

Vn

and

let

0:

E

lit

(i) gat",(d) is

fi

1

-embeddable (resp.

fi

1

-rigid)

if

and

only

if

0:

2:

0

and

d is

fi1

-embeddable (resp.

fi1

-rigid).

(ii) gat",(d) is hypercube embeddable (resp. h-rigid)

if

and

only

if

0:

E

Z+

and

d is hypercube embeddable (resp. h-rigid).

(iii) gat",(d) E £n+1

if

and

only

if

0:

E Z

and

d E

£n.

(iv) gat",(d) is

hypermetric

(resp.

of

negative type)

if

and

only

if

0:

2:

0

and

d

is

hypermetric

(resp.

of

negative type). I

7.2

The

Antipodal

Extension

Operation

Let

d

be

a

distance

on

the

set

Vn

= {1,

...

,

n}

and

let

0:

E

lllr.

We define a

distance

d'

on

the

set

Vn+

1 =

Vn

U

{n

+

1}

by

setting

(7.2.1)

{

d'(1,n+1)

=0:,

d'(i,n+1)

=o:-d(l,i)

d'(i,j)

=

d(i,j)

for 2

~

i

~

n,

for 1

~

i < j

~

n.

The

distance

d' is called

an

antipodal

extension

of

d

and

is

denoted

by

ant",(d).

(Compare

with

the

definition

of

the

gate

extension

gat",(d) from (7.1.1).)

Note

that

ant",(d) satisfies

the

triangle

equalities:

(7.2.2)

d'(l,

n +

1)

=

d'(l,

i) + d'(i, n +

1)

for all i =

2,

...

,n

(so,

the

new

point

"n

+ 1" is

"antipodal"

to

the

point

"1").

If

we

apply

the

antipodal

extension

operation

iteratively

n

times,

starting

from

d,

we

obtain

a

distance

on

2n

points,

denoted

by

Ant",(d),

and

called

the

full

antipodal

extension

of

d.

So, Ant",(d) is defined by

(7.2.3)

{

Ant",(d)(i,n+i)

Ant",(d)(i,

n +

j)

Ant",(d)(i,j)

Ant",(n

+ i, n +

j)

=0:

=

0:

-

d(i,j)

=

d(i,j)

=

d(i,j)

for 1

~

i

~

n,

for 1

~

i

=I

j

~

n,

for 1

~

i

=I

j

~

n,

for 1

~

i

=I

j

~

n.

These

two

operations

are

treated

in

detail

in

Deza

and

Laurent

[1992e].

7.2

The

Antipodal Extension Operation

95

Observe

that,

if d

LSES

>-'s6(S),

where S is a collection of nonempty

proper

subsets

of

V

n

,

then

anta(d)

L

>-'s6(S

U

{n

+

1})

+ L

>-'sb(S)

SESII~S

SESIIES

+(a

L>-'s)b({n+l}).

(7.2.4)

SES

Conversely, every decomposition of ant",(d) as a nonnegative combination

of

nonzero

cut

semimetrics is of

the

form (7.2.4), since ant",(d) satisfies

the

triangle

equalities (7.2.2) for

i

2,

...

, n.

In

particular, if ant", (

d)

is iI-embeddable,

then

the

size

of

any of its 114-realizations

is

equal to

a.

Similarly, any 114-realization

of

Ant",(d) is

of

the form

(7.2.5)

Anta(d)

L>-'s6(SUS*)+(a-

L>-'s)b({n+l,

...

,2n}),

SES SES

where

we

set

S·

:=

{n

+

iii

E

Vn

and i

rt.

S}.

These observations

permit

to

establish the next result.

Proposition

1.2.6.

Let

d

be

a distance

on

Vn

and a E

llt

(i)

anta(d)

(resp. Ant",(d)) is ii-embeddable

if

and only

if

a

~

Stl

(d)

and

dis

ii-embeddable. Moreover, ant",(d) (resp. Ant",(d)) is

ii-rigid

if

and

only

if

d is

ii-rigid.

(ii) ant",(d) (resp. Ant",(d)) is hypercube embeddable

if

and

only

if

d is hy-

percube embeddable,

a E Z+, and a

~

shed). Moreover, ant",(d) (resp.

Anta(d))

is h-rigid

if

and only

if

d is h-rigid.

(iii) ant",(d) (resp.

Anta(d))

belongs to £n+1

if

and only

if

dE

£n

and a E Z.

I

Proposition 7.2.6

is

a useful tool; it permits, for instance, to construct exam-

ples of semimetrics

that

are

ii-embeddable

and

belong to the

cut

lattice,

but

are

not

hypercube embeddable. Indeed, let d be a hypercube embeddable distance

and

suppose

that

we

can find

an

integer a such

that

sel

(d)

s:

a <

shed).

Then,

ant", (

d)

is

ii-embeddable

and belongs to the

cut

lattice,

but

is not hyper-

cube

embeddable.

Example

1.2.1.

Let

21n

denote the distance on

Vn

that

takes

the

value 2 on

all pairs.

Then,

for n

~

5,

sh(21

n

)

nand

13£1

(21n) < 4 (see Example 4.3.7

and

Section 7.4). Therefore, for n

~

5,

the

metric ant4(21n) (which takes value

2

on

all pairs except value 4 on one pair) is iI-embeddable, belongs to the

cut

lattice,

but

is

not hypercube embeddable. (The metric Ant4(21n) has

the

same

properties.) Moreover,

the

metric ant4(21n) is

ii-rigid

if

and

only if

2l

n

is i

l

-

rigid, i.e., n =

3.

I

96

Chapter

7.

Operations

13,4)

CD-CD-®----&----0

I 1,2,3,4) 12,3,4) 13,4) ( 4 )

f2f

12'133"44))~

2 3

C1Z

14

S

')

f2f

11,2,3,4} 0

~

I l

{I'2'3,4'5]~)&J

IS}

9 7

1I,2,3,5} 8 {l,5}

{1,2,5}

Figure

7.2.8:

Hypercube

embeddings

of

the

path

P

5

and

the

circuit 010

Example

7.2.9.

There

are

many

examples

of

graphs G whose

path

metric

de

can

be

constructed

as

the

antipodal

extension

of

the

path

metric

of

another

graph.

For instance, let

Kn+l

\e

denote

the

complete

graph

on n + 1 nodes

with

one deleted edge.

Then,

This

example

will

be

treated

in

detail

in

Sectiun 7.4,

tugether

with

the

ca~e

of

the

cocktail-party

graph.

The

path

metric

d[

of

the

I-skeleton

graph

of

the

icosahedron (see, e.g., Brouwer,

Cohen

and

Neumaier

[1989]

for a description

of

this

graph)

can

be

expressed as

where

'V0

5

is

the

graph

obtained

by adding a new node adjacent

to

all nodes

of

the

5-circuit 0

5

•

In

fact,

d[

is R1-rigid; see Deza

and

Laurent

[I994a]. Also,

d(H(n,

2)) =

Ant

n

(d(H(n

-

1,2)))

= Ant

n

(2d

GH(n,

2)))

where

~H(n,

2)

is

the

half-cube graph. Let P

n

= (1,2,

...

, n)

and

On

= (1,2,

...

, n)

denote

the

path

and

the

circuit

on

n nodes.

Then,

One

can

easily verify (see also

Example

19.1.4)

that

d(Pn)=

L

8({I,2,

...

,i-I,i}),

l:::;i$n-l

which, by (7.2.5), implies

d(02n) = L 8(

{I,

2,

...

,i-I,

i,

n+i+I,

n+i+2,

...

,2n-I,

2n}

)+8(

{I,

...

,n}).

l$i$n-l

Figure

7.2.8 shows

the

path

P

5

and

the

circuit 010 together

with

a labeling

of

their

nodes (by sets) providing

the

R1-embeddings shown above. I

7.3

The

Spherical Extension Operation

97

7.3

The

Spherical

Extension

Operation

Let d

be

a distance on

Vn

and

let t E .

We

define a distance d' on Vn+l =

Vn

U

{n

+ I} by setting

(7.3.1)

{

d'(i,n

+ 1)

d'(i,j)

t

d(i,j)

for 1 i n,

for 1

:5

i < j n.

The

distance d' is called the spherical

t·extension

of d

and

is denoted

by

spht(d).

This

operation is considered in Deza

and

Grishukhin

[1994].

Proposition

7.3.2.

Let

d

be

a distance

on

Vn

and

let t E

Rt·.

(i) spht(d) is a

semimetric

if

and only

if

2t

~

max(d(i,j)

11

i < j

:5

n)

and

d is a

semimetric.

(ii) spht(d) E

£n+!

if

and only

if

t E Z and

d(i,j)

is an even integer

for

all

1

:5

i < j

:5

n.

(iii)

If

dis

Prembeddable and

2t

2::

Sil(d),

then

spht(d) is ll-embeddable.

(iv)

If

d

is

hypercube embeddable

and

2t

~

shed),

then

2 . spht(d) is hypercube

embeddable.

Proof.

(i), (ii) are immediate. For (iii), note

that

spht(d) =

!(ant2t(d)+gato(d)).

Hence,

if

dis

ll-embeddable

and

2t

2::

Sil(d),

then

ant2t(d) is

ll-embeddable

by

Proposition

7.2.6

and

gato(d) isl1-embeddable by Proposition 7.1.2.

This

implies

that

spht(d) is lI-embeddable.

The

proof is identical

for

(iv). I

For

an

integer m

~

2, define recursively

sp~m(d)

as

Spht(sp~m-l(d)),

after

setting

sphi(d)

spht(d).

Lemma

7.3.3.

Let

d

be

a distance

on

Vn

and

t E

114.

If

d is ll-embeddable

and

2t

~

Sfl

(d),

then

sp~m(d)

is Pl-embeddable

for

each integer m

2::

1. Moreover,

2t

t

(hm(d))

2 2t -

Sfl

(d)

:5

Sll sp.'t

:5

t - 2

m

.

Proof. As spht(d)

!(ant2t(d)+gato(d)),

we

can find a 114-realization

ofspht(d)

of

size

!(2t

+

Sll

(d)),

1

Sfl

(spht(d))

:5

t +

"2Sfl

(d).

Hence, Sll (spht(d))

:5

2t, implying

that

sph;(d) is PI-embeddable. Therefore,

sphr'(d)

is

ll-embeddable

for all m

~

1.

The

upper

bound

from Lemma 7.3.3

follows easily

by

induction. For the lower bound, note

that

sphr'(d)

contains

as a

sub

distance

the

equidistant metric

tim

(taking the same value t

on

m

points). Therefore,

Sll

(sphr'

(d))

2::

Sfl

(tim),

where

S£l

(tim)

= 2t - m (see,

e.g., Section 7.4).

I

98

Chapter

7.

Operations

In

particular,

if

dis

t'l-embeddable

and

2t

:::::

St,

(d),

then

lim St,(sphr'(d)) = 2t.

m--.(X)

Fichet

[1992]

defines

the

t'1-radiu8 r(d) of

an

t'l-embeddable

distance

d as

the

smallest

scalar t > 0 such

that

spht(d) is t'l-embeddable.

Thus,

1 1

-2

maXdij

::;

r(d)

::;

-2

St, (d).

',}

For some examples

of

metrics (e.g., ultrametrics,

path

metrics of

paths,

etc.)

equality

holds

with

the

lower

bound.

We refer

to

Section 14.4 for

the

study

of conditions

under

which

the

spherical

extension

operation

preserves

other

metric properties, such as

hypermetricity

or

the

negative

type

property.

7.4

An

Example:

The

Cocktail-Party

Graph

We

present

here some examples which apply,

in

particular,

the

properties

of

the

antipodal

extension operation. Namely,

we

show how to

obtain

t'l-embeddings

for

the

path

metrics of

the

graph

Kn+l

\e

and

of

the

cocktail-party

graph

Knx2

in

terms

of

t'rembeddings

of

the

complete

graph

Kn.

Let us consider

the

equidistant

metric

In,

that

takes

the

value 1 for all pairs.

Hence,

In

coincides

with

the

path

metric

of

the

complete

graph

Kn.

Let

denote

the

distance

on

V

n

+

1

=

Vn

U

{n

+

I}

obtained

by

taking

the

antipodal

extension

ant",(l

n

) of

In

with

parameter

a =

2.

So, d

n

takes

the

value 1

on

all

pairs

except value 2

on

the

pair

(1, n + 1). Hence, d

n

coincides

with

the

path

metric

of

the

graph

Kn+l

\e,

obtained

by deleting

the

edge e

:=

(1, n + 1) from

the

complete

graph

on

V

n

+

1

•

Let

denote

the

distance

on

V2n

=

Vn

U

{n

+

1,

...

, 2n}

obtained

by

taking

the

full

antipodal

extension

Ant",(ln)

of

In

with

a = 2 (recall (7.2.3)). So,

d~

takes

value 1

on

all pairs except value 2

on

the

n pairs:

(l,n

+ 1),

...

, (n, 2n). Hence,

d~

coincides

with

the

path

metric of

the

cocktail-party

graph

K

nx2

.

We now see how

to

construct

t'rembeddings

of

the

metrics d

n

and

d~.

In

order

to

be able

to

apply

Proposition

7.2.6

and

relation

(7.2.4),

we

need

to

find

an

t'l-decomposition of

In

whose size

is

less

than

or equal

to

2.

Clearly,

the

distance

In

can

always

be

decomposed as

(7.4.1)

1

In

= -

2:

8(i),

2

l~i~n

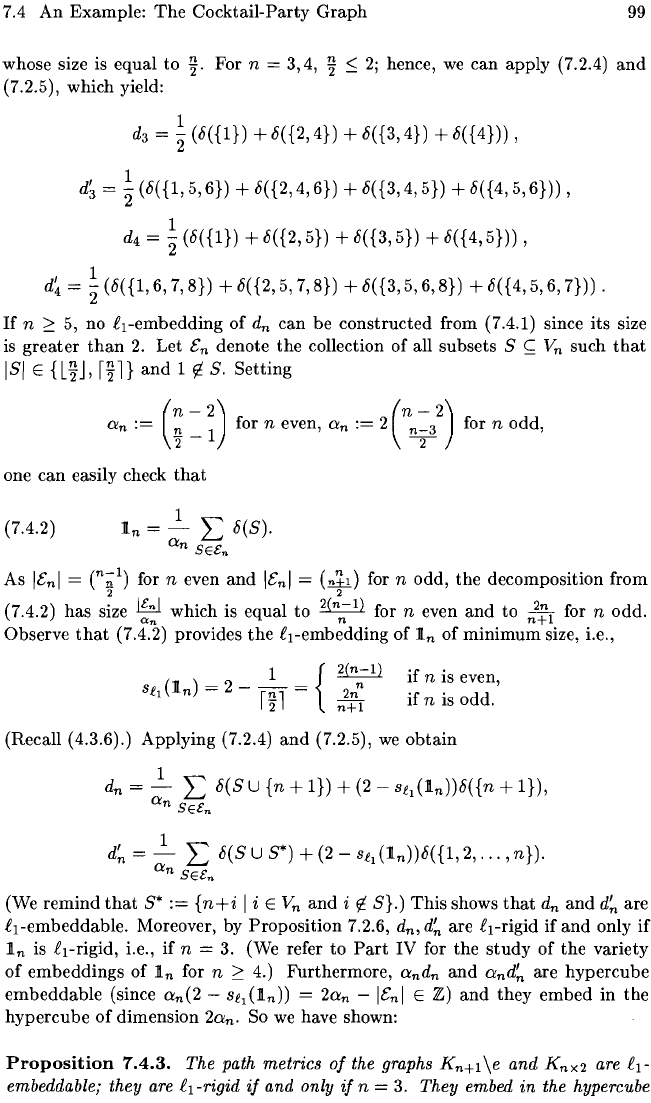
7.4 An Example:

The

Cocktail-Party

Graph

99

whose size is equal to

~.

For n = 3,4,

~

:::;

2;

hence,

we

can apply (7.2.4)

and

(7.2.5), which yield:

d

3

=

~

(0

( { 1 } ) + 0 (

{2,

4}

) + 0 (

{3,

4}

) + 0 ( { 4 }

))

,

d~

=

~(0({1,5,6})

+0({2,4,6}) +0({3,4,5})

+0({4,5,6})),

1

d4

="2

(0({1})

+0({2,5}) +0({3,5})

+0({4,5})),

d~

=

~

(0({1,6, 7,8})

+0({2,5,

7,8})

+0({3,5,6,8})

+0({4,5,6,

7})).

If

n

2:

5, no £l-embedding

of

d

n

can be constructed from (7.4.1) since its size

is

greater

than

2.

Let

En

denote the collection

of

all subsets S

~

Vn

such

that

lSI

E

{L~J,

I~l}

and

1

rf-

S. Setting

(

n-2)

(n-2)

a

n

:=

~

_ 1 for n even, an

:=

2

n;-3

for n odd,

one can easily check

that

1

:an

= -

~

o(S).

an

SEen

(7.4.2)

As

IEnl

=

(n;;-l)

for n even

and

IEnl

=

(~)

for n odd, the decomposition from

2 2

(7.4.2) has size

~

which is equal to

2(n-l)

for n even

and

to

2..;'1

for n odd.

Observe

that

(7.4.'2)

provides

the

£l-emb;dding

of

:an

of

minimu~

size, i.e.,

if

n is even,

if

n

is

odd.

(Recall (4.3.6).) Applying (7.2.4)

and

(7.2.5),

we

obtain

1

d

n

= -

~

o(SU

{n

+ 1}) +

(2

-

s£,(ln))o({n

+ 1}),

an SEen

(We

remind

that

S*

:=

{n+i

liE

Vn

and

i

rf-

S}.)

This

shows

that

d

n

and

d~

are

£l-embeddable. Moreover, by Proposition 7.2.6,

d

n

,

d~

are £l-rigid

if

and

only

if

In

is

£l-rigid, i.e.,

if

n = 3. (We refer to

Part

IV for the

study

of

the variety

of

embeddings

of

In

for n

2:

4.) Furthermore,

and

n

and

and~

are hypercube

embeddable

(since a

n

(2

-

s£,

(In)) =

2a

n

-

IEnl

E Z)

and

they embed in the

hypercube

of

dimension

2a

n

.

So

we

have shown:

Proposition

1.4.3.

The path

metrics

of

the graphs

Kn+1

\e

and

Knx2

are

£1-

embeddable; they are

£1

-rigid

if

and only

if

n = 3. They embed

in

the hypercube

100

Chapter

7.

Operations

of

dimension

2a

n

with the scale

an.

For instance, for n 5,

the

above decompositions for

d5,

d

s

read:

d

5

=

~

[8({2,3,6})

+8({2,4,6})

+ 8({2,5,6})

+8({3,4,6})

+ 8({3,5,6})]

+k

[8(

{4, 5, 6}) + 8( {2,

3,

4,

6}) +

8(

{2,4,

5,

6})

+

8(

{2,

3,

5,

6})]

+~8({3,4,5,6})+

t8(6),

d~

= k

[8({2,3,6,9,IO})+

8({2,4,6,8,

IO})

+

8({2,5,6,8,9})

+ 8({3,4,6,

7,

1O})]

+~

[8({3,5,6, 7,9})

+8({4,5,6,

7,8}) + 8({2,3,4,6,

IO})

+ 8({2,3,5,6,9})]

+~

[8(

{2,

4,5,6,

8}) + 8( {3,

4,

5,6,

7})]

+

k8(

{I,

2,3, 4, 5}).

Another

[I-embedding

of

d5

is given, for instance, by

d5=~(8({1})+8({6})+

E

8({1'i,j})),

2:5:t<j:5:5

I

Therefore,

the

minimum

scale

of

d

5

is equal

to

4. Indeed,

the

minimum

scale

7)(d

n

)

of d

n

is clearly

an

even integer. Moreover,

7)(d

5

)

f:.

2 since 2d

5

is

not

hypercube embeddable (because 2d

s

=

ant4(2:D.5)

and

4 <

sh(21s),

as

sh(215)

5 by

Theorem

22.0.6).

In

fact, one

can

check (Deza

and

Grishukhin [1994])

that

4d5

has three distinct (up to

permutation)

Z+-realizations. Besides

the

above

one,

they

are

4d

5

= E 8({1,i})

+8({i,6}),

and

2:5:i:5:S

4d5

8({1}) + 8({1,j}) +

8({i,j,6})

+ 8({i,6}),

iE{2,3,4,5}

\

{j}

for

any

j E

{2,3,4,5}.

So

we

know

the

minimum

scale

7)(

d

n

)

of

d

n

for n =

3,4,5:

(These facts were already observed by Blake

and

Gilchrist [19731.) We also have

the

following (very loose) upper bound:

7)(d

n

)

::;

an,

from Proposition 7.4.3. A

better

bound:

1J(d

n

) < n is provided by

the

next result from Shpectorov [1993].

Lemma

7.4.4.

For

an

integer k

2,

the path

metric

of

the cocktail-party graph

K2k

x2

embeds isometrically

into

the hypercube

of

dimension

2k

with the scale

2k-l.

Hence,

if

< n 2k, then

2k-ld(Knx2)

is

hypercube embeddable.

Therefore,

7)(d

n

),

7)(d~)

<

n.

Proof. Consider

the

vector space

GF(2)k

over the two-element field

GF(2)

=

{O,l}. Every hyperplane

in

GF(2)k

consists

of2

k

-

1

points

and

the

symmetric

difference

of

two hyperplanes also contains 2

k

-

1

points. We

obtain

a hypercube

embedding

of

d(K2kX2)

with

the

scale in

the

hypercube {a, I Fk by labeling

the

nodes by

the

2k - 1 hyperplanes, together

with

their

complements,

the

full

7.5

The

Direct

Product

and

the

Tensor

Product

Operations

101

set

GF(2)k,

and

0.

I

Given

an

integer t E

Z+,

note

that

is

hypercube

embeddable

if

and

only if

4t

2:

sh(2tl

n

).

Hence,

the

minimum

scale

of

d

n

can

be

expressed as

(7.4.5)

Therefore, in order

to

determine

the

minimum

scale

TJ(d

n

),

we

need

to

know

the

minimum

h-size

sh(2tl

n

)

of

the

equidistant

metric

2tl

n

,

for t E

Z+.

This

question

is

considered

in

detail

in

Chapter

23;

see,

in

particular,

Section 23.3.

The

quantity

sh(2tl

n

)

is

not

known

in

general.

Its

exact

computation

is a

hard

problem. Indeed, for some choices

of

the

parameters

nand

t,

it

relies

on

the

question

of

existence

of

some classes

of

designs such as projective planes or

Hadamard

designs. For instance,

Sh

(2tlt2+t+!)

= t

2

+ t + 1

if

and

only

if

there

exists a projective

plane

of order t,

and

sh(2t14t)

=

4t

- 1

if

and

only

if

there

exists a

Hadamard

matrix

of order

4t

(see

Proposition

23.3.2). Nevertheless,

some results are known. We

quote

here some

of

them,

more

can

be

found

in

Part

IV.

(i)

sh(2tl

n

)

2:

n - 1

with

equality

if

and

only

if

n =

4t

and

there

exists a

Hadamard

matrix

of

order

4t.

(ii)

Sh

(2tln)

=

i4t

-

r¥ll

if

n

:::;

4t

:::;

80.

(See

Theorem

23.3.1

and

Corollary 23.3.6.)

This

implies:

Lemma

1.4.6.

We

have:

2i~1

:::;

TJ(d

n

)

<

n.

Moreover,

TJ(d

n

)

=

2i~1

ifn

:::;

80;

and

TJ(

d

4t

) =

2t

if

and

only

if

there

exists

a

Hadamard

matrix

of

order

4t.

I

7.5

The

Direct

Product

and

Tensor

Product

Oper-

ations

We present two operations:

the

direct

product

and

the

tensor

product,

which

preserve, respectively,

ll-embeddability

and

{O,

l}-covariances or, equivalently,

the

cut

cone

and

the

correlation cone.

Definition

1.5.I.

(i)

Let

(Xl,

dJ)

and

(X2' d

2

)

be

two distance spaces.

Their

direct

product

is

the

distance

space

(Xl

x X

2

, d

l

EEl

d2) where,

for

Xl,

YI

E

XI,

X2,

Y2

E X

2

,

102

Chapter

7.

Operations

(ii) Let

PI:

Xl

XXI

-->

lR

andp2 : X

2

xX

2

lR

be

two symmetric functions.

Their

tensor product is the symmetric function

For

path

metrics,

the

direct product operation corresponds to

the

Cartesian

product

of graphs. Namely, if G and H are two connected graphs,

then

the

direct

product

of their

path

metrics coincides with

the

path

metric of the Cartesian

product

of

G and

H.

Proposition

7.5.2.

Let d

i

be

a distance on the set

Xi,

for i 1,2.

(i)

(Xl

x X

2

,

d

l

EEl

d

2

)

is £l-embeddable (resp.

£1

-rigid, hypercube embeddable,

h-rigid)

if

and only

if

(Xl,

d

l

) and (X2' d

2

)

are

£l-embeddable

(re.~p.

£1-

rigid, hypercube embeddable, h-rigid).

(ii)

(Xl

x X

2

,

d

l

EEl

d

2

)

is

hypermetric (resp.

of

negative type)

if

and only

if

(Xl,d

l

) and

(X

2

,d

2

)

are

hypermetric (resp.

of

negative type).

Proof.

The

proof of

(1)

is based on the following two observations:

•

If

d

l

=

LS~Xl

as8(S)

and

d

2

=

LT~Xl

f3To(T),

then

d

l

EEl

d

2

= L

aso(S

x X

2

)

+ L fJr8(Xl X

T).

Sr;X,

T~X2

• Let

Pi

denote

the

projection from

Xl

X X

2

to

Xi,

for i = 1,2. Suppose

that

d

l

EEl

d

2

= L AA8(A)

AEA

with

AA

> 0 for A E

A,

where A is a collection of proper subsets of X I X X2.

Then,

for each A E

A,

A =

PI

(A) x P2(A) with Pl(A) =

Xl

or P2(A) = X

2

•

This

can

be

seen from

the

fact

that

d

l

EEl

d

2

satisfies the triangle equalities:

d(

(Xl,

X2),

(Yl,

Y2»

=

d«xI,

X2),

(Yl,

X2»

+

d«Yll

X2),

(Yb Y2»,

d«XI'

X2),

(Yl>

Y2»

d«xI,

X2),

(Xl,

Y2»

+

d«Xl,

Y2),(Yl,

Y2»

for all

Xl>

Yl

EX},

x2,

Y2

E X2. Hence,

d;

=

LAEA

AA8(pi(A» for i = 1,2.

We

prove (li) in the hypermetric case (the negative

type

case is similar).

If

(Xl

x

X2J

d

l

EEld2)

is hypermetric,

then

so

is

(Xl,

d

1

),

as

it

is

isomorphic to the subspace

(Xl

x

{x2},d

1

ffid

2

) (where

X2

E X

2

).

Conversely suppose

that

both

(Xl,d

1

)

and

(X

2

,d

2

)

are hypermetric. Let b E with

L(Xl,Xl)EX,XXl

b(xl,x2)

= 1.

Define a E

ZXl

and

c E ZXz by setting

a

X,

:=

L

b(xl,x2)

for

Xl

E

Xl,

c

xz

:=

L b(Xl,X2) for

X2

E X2·

"'2EXz

""EX,

Deza M.M., Laurent M. Geometry of Cuts and Metrics

Подождите немного. Документ загружается.