Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.

30.4
The
Parachute
Inequality
499
(a) 5 =
{2',4',
...
,(k
-l)',k}
U
T,
where T is a subset
of
{1,2,
...
,k
- 2}
alternated along the path (1,2,
...
, k - 2).
(b) 5 =
{k,1',(k-1)'}UTUT',
where T is a subset
of{2,3,
...
,k-2}
which is alternated along the path (2,3,
...
, k - 2),
and
T'
is a subset
of
{2' , 3',
...
,
(k
- 2)'}
for
which
T'
U
{I',
(k
- I)'} is pseudo-alternated along
the path
(1',2',
...
,
(k
- 1)').
Type
3':
similar
to
Type
3, exchanging nodes
i,
i'
for
all i = 1,
...
, k.
Therefore, the total
number
of
roots
of
(
Par
2k+l)T
x
::;
0 is equal
to
hk+2k/k-l
+
2/k-2
+ 2k - 1
for
k odd and
to
12k
+ 2k - 1
for
k even, while the
number
of
nonzero
symmetric
roots
of
(Par2k+lf
x
::;
0 is equal
to
the Fibonacci
number
/k.
Proof. Let 5 be a subset
of
{I,
...
,
k,
1',
...
,
k'}
and
set s
:=
15
n
{I,
...
, k -
1}1,
s'
:=
15
n
{I',
...
, (k -
1),}1.
One
checks easily
that
(Par2k+l)T 8(5) =
18(5)
n
PI
-
2(s
+
s'),
if k, k'
rt
5
=
18(5)
n
PI
- 2s - k,
if
k E 5,
k'
rt
5
= 18(5) n
PI
-
2(k
- 1),
if
k, k' E 5
Then,
it
is easy
to
see
that,
for k
odd,
the
parachute
inequality
is
valid
and
that,
for
any
k,
the
roots
of
(Par2k+l)T x::; 0 are indeed
of
Types
1,2,3, or 3'.
There
are
2k
- 1
roots
of
Type
1,
12k
roots
of
Type
2
and
/k
+
(k
-l)/k-l
roots
of
Type
3.
Hence, altogether,
there
are 2k
-1
+
12k
+2/k
+2(k
-l)/k-l
roots for k
odd,
and
2k
-1
+
12k
roots for k even.
There
is
only one
symmetric
root
of
Type
1, namely,
8({k,
...
, 3, 1, 1', 3',
...
,k'})
for k
odd
and
8({k,
...
,4,2,2',4',
...
,
k'})
for k even.
The
number
of
symmetric
roots
of
Type
2
is
equal
to
the
number
of
alternated
subsets
along
the
path
(2,3,
...
, k - 1), Le.,
to
/k.
There
are no
symmetric
roots
of
Type
3
or
3'. Therefore, in
total,
there
are
/k
nonzero
symmetric
roots. I
We now show a connection between
the
parachute
inequality
(Par2k+lf
x
::;
0
and
the
clique-web inequality
CW~k~l
(1,
...
,1,
-1,
-If
x
::;
o.
For this, let us
first define
the
following inequality:
(30.4.6)
L
Xij
- L (XOi + XOi') - L (XO'i +
XO'i')
::; 0,
ijEQ
l::;i::;k-l
1::;i::;k-2
which
is
defined
on
the
2k nodes
of
the
set
{O,
1,
2,
...
, k - 1,0', 1',
...
,
(k
-
I)').
The
inequality (30.4.6)
is
called
the
Fibonacci inequality
and
is
denoted
as
(Fib
2
k)T x
::;
O.
Consider now
the
clique-web inequality
CW~k~l(l,
...
,l,-l,-l)Tx
::;
o.
Then,
the
inequality
obtained
from
it
by collapsing a positive
node
(Le., a node i
for which
bi
=
1)
and
a negative node (Le., a node j for which
bj
=
-1)
coincides
with
the
Fibonacci inequality
(Fib
2
k)T x
::;
0 (if one labels in a suitable way
the
points
on
which
the
clique-web inequality
is
defined).
This
shows,
in
particular,
that
the
Fibonacci inequality
is
valid for
CUT
2k
.
Observe
that
the
Fibonacci inequality
(Fib
2
kf
x
::;
0
can
also be
obtained
from
the
parachute
inequality (Par2k+l)T x::; 0 by collapsing
the
two nodes k,
k'

500
Chapter
30.
Other
Valid Inequalities
and
Facets
into a single node denoted as
0
1
•
Therefore, the roots of (Fib
2k
,)T x
:::;
0 are
the
cut
vectors
6(
S \ {k, k/} U {O/}) for S of
Type
1
and
the
cut
vectors
6(
S)
for S
of
Type
2. Hence, (Fib
2
kf
x
~
0 has
12k
+ 2k 1 roots.
It
can
be checked
that
it
defines a face of
CUT
2k
of
rank
ek;-l)
+ 2
e;)
(2k - 3).
Therefore, for any k
;:::
3, the parachute inequality (Par2k+l f x
:::;
0
and
the
clique-web inequality
CW~k~l
(1,
...
,1,
-1,
_l)T
x
~
0
admit
a common collaps-
ing.
Figures 30.4.7
and
30.4.8 show, respectively,
the
support
graphs of
the
Fi-
bonacci inequality
(Fib
6
)T x
:::;
0
and
of
the
clique-web inequality
(CW~)T
x:::;
O.
(Collapse
the
nodes 0
'
and
0" in
(CW~)Tx:::;
0 to
obtain
(Fib
6
)T
x
~
0.)
o
..
/,!':,-.,
0'
" "
\.
""'-
.'
2'
, 1
2
Figure 30.4.8:
(CW~fx:::;
0
30.4.2
Generalizing
the
Parachute
Inequality
Finally,
we
present a class of inequalities from Boissin
[1994]
generalizing
the
parachute
inequality. These new inequalities can
be
obtained by applying
the
operation
of
"duplicating a node", described
in
Section 26.6. As
this
operation
is easier
to
apply
to
facets of
the
correlation polytope,
we
first reformulate
the
parachute
inequality for
the
correlation polytope.
We
start
with
the
parachute inequality (Par2k+1)T x:::;
0,
which is defined on
the
set
V2k+l
{O,
1,
2,
...
, k,
11,
2/,
...
, k'}.
If
we
apply
the
covariance
mapping
~kl
(pointed
at
position k'),
then
we
obtain
the
following inequality
aT
P
;:::
0,
which is defined on all pairs
of
(nonnecessarly distinct) elements of V
2
k+l
\ {k'}:
(30.4.9)
(k
l)poo
+ k';./Pkk +
L:
Pij
ijEE(P')
10-1
L:
(Po
11.
+
PO,h.'
+ Pk,h.')
;:::
0,
11.=1
where
pi
denotes
the
path
(k, k
1,
...
,2,1,
1',2
'
,
...
, (k - 1)'). Figure 30.4.4
shows
the
quantity
aT
P for k 3 (the loops
at
nodes 0
and
3 indicate
the
values
of
aoo
and
a33)'
Let
h E
{I,
...
, k I}
and
let b
T
P
;:::
0 denote
the
inequality
obtained
from
30.4
The
Parachute
Inequality
501
aT
p
2:
0 by
duplicating
node
h; recall
the
definition of b from
relation
(26.6.3).
Hence,
if
we
denote
the
new
node
by h*,
then
b
ij
=
aij
for
i,j
E V
2
k+l
\
{k'},
bh*,h*
= 0,
bO,h*
=
-1
and,
for i E V
2
k+l
\
{O,
k'},
bi,h*
= 1
if
i is
adjacent
to
h
on
the
path
P'
and
bi,h*
= 0 otherwise.
It
is easy
to
check
that
one
should
set
bh,h*
= 1 in order
to
ensure
that
the
inequality b
T
p
2:
0 defines a facet of
COR
2
k+l (see
Proposition
26.6.4).
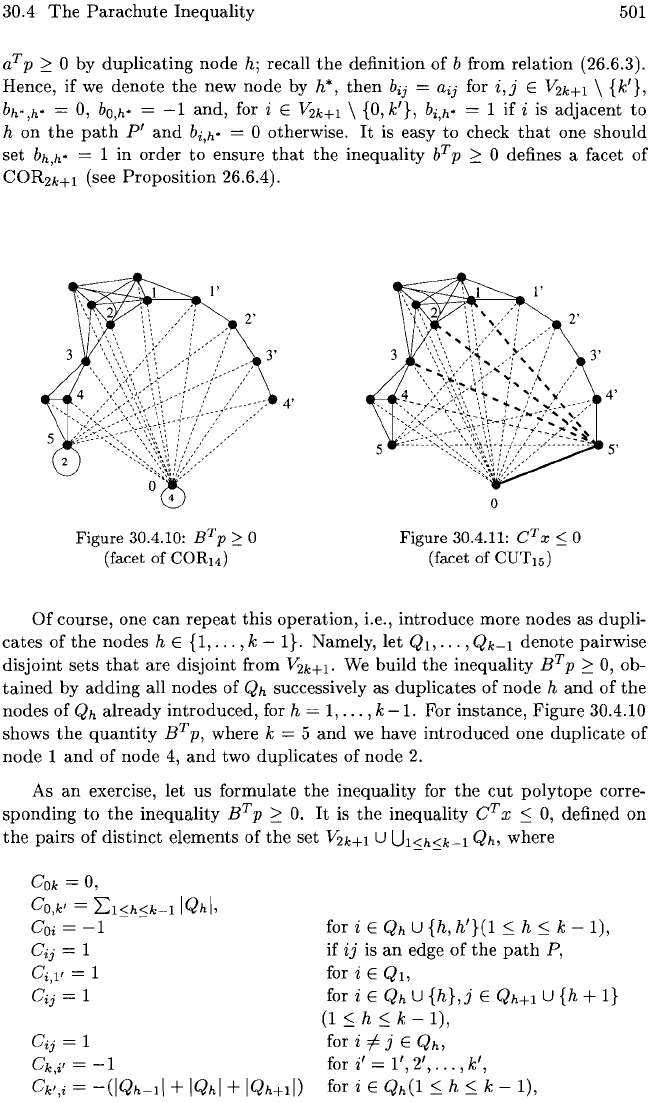
Figure
30.4.10:
BT
p
::::
0
(facet of COR
I4
)
o
Figure
30.4.11: C
T
x
:s;
0
(facet of CUTIS)
4'
5'
Of
course, one
can
repeat
this
operation,
Le.,
introduce
more
nodes as dupli-
cates
of
the
nodes h E
{I,
...
, k - I}. Namely, let
Ql"'"
Qk-l
denote
pairwise
disjoint sets
that
are
disjoint from V
2k
+l'
We
build
the
inequality
BT
p
2:
0, ob-
tained
by
adding
all nodes of Qh successively as duplicates of
node
h
and
of
the
nodes of Qh
already
introduced,
for h =
1,
...
, k
-1.
For instance,
Figure
30.4.10
shows
the
quantity
BT
p,
where k = 5
and
we
have
introduced
one
duplicate
of
node
1
and
of
node
4,
and
two duplicates of
node
2.
As
an
exercise, let
us
formulate
the
inequality for
the
cut
polytope
corre-
sponding
to
the
inequality
BT
p
2:
O.
It
is
the
inequality C
T
x
~
0, defined
on
the
pairs
of
distinct
elements of
the
set V
2
k+l
U Ul:;h:;k-l Qh, where
COk
= 0,
CO,k'
=
Ll<h<k-l
IQhl,
COi
=
-1
- -
Cij
= 1
C
i
,1' = 1
Cij
= 1
C
ij
= 1
Ck,i' =
-1
Ck',i
= -(IQh-11 +
IQhl
+ IQh+ll)
for i E Qh U {h,
h'}(l
:s;,
h
:s;
k - 1),
if
ij
is
an
edge
of
the
path
P,
for i E Ql,
for i E Qh U
{h},j
E Qh+l U
{h
+
I}
(1:s;,h:s;,k-1),
for i
=1=
j E Qh,
for
i'
=
1',2',
...
,
k',
for i E Qh(l:s;,
h:s;,
k - 1),

502
Chapter
30.
Other
Valid Inequalities and Facets
setting
Qo
=
Qk
=
0.
For instance, the inequality
BT
p
?:
0 from Figure 30.4.10
corresponds to the inequality
C
T
x
:::;
0,
which is shown in Figure 30.4.11 (with
weight 4 on edge (5',0), weight
-4
on edges (5',1),
(5
'
,2), (5',3) and weight
-2
on edge (5',4)).
The
next result
is
a direct application of Proposition 26.6.4.
Theorem
30.4.12.
The inequality
BT
p
?:
0 defines a facet
of
the correla-
tion polytope. Equivalently, the inequality C
T
x
:::;
0 defines a facet
of
the
cut
polytope. I
30.5
Some
Sporadic
Examples
Grishukhin
[1990]
introduced the following inequality;
(30.5.1)
L
Xij
+
x56
+
x57
-
x67
- X16 -
x36
-
x27
X47 2
1.si<j~4
and
proved
that
it defines a facet of GUT7.
We
also denote the inequality (30.5.1)
as (Gr7)T
x
:::;
O.
Note
that,
if
we
collapse
both
nodes 6,7 in (Gr7
JT
x:::; 0,
then
we
obtain the hypermetric inequality Q6(I,
1,1,1,
-2,
_l)T
x
:::;
O.
In
other words,
GrT
x
:::;
0
can
be seen as a lifting of the inequality Q6(I, I,
1,1,
_I)T
x
:::;
O.
On
the
other
hand, consider the following inequality (30.5.2), denoted as
(Grs)T
x
:::;
0;
it
is
introduced in De Simone, Deza
and
Laurent
[1994]
and
shown
to be a facet of
GeTs;
(30.5.2)
Observe
that,
if
we
collapse
both
nodes 5,8
in
(Grg)T x:::; 0,
we
obtain (Gr7JT x
:::;
O.
Hence, (Gr7)T x
:::;
0 is a nonpure inequality
that
comes as collapsingofthe pure
inequality (GrS)T
x
:::;
O.
Figures 30.5.3, 30.5.4 show, respectively,
the
support
graphs of
the
inequalities (Gr7)T x
:::;
0, (GrS)T x
:::;
o.
(In Figure 30.5.3,
the
thick
dotted
edge between node 5 and the circle enclosing nodes 1,2,3,4 indicates
that
node 5
is
joined to all four nodes 1,2,3,4 by
an
edge with weight -2.)
6 7
6 7
~
~i
3 : 4
•
5
5
Figure 30.5.3: (Gr7)T x
:::;
0
-2
. -
--.
-1
.-------.
1
-------
edge weights

30.6
Complete
Description for n
:::;
7
503
Kelly (unpublished manuscript) introduced the following class
of
valid in-
equalities. Consider a
partition
of
the
set {1,
...
,
n}
into P U Q U
{n},
where
IFI
p,IQI
q
with
p,q
2:
2
and
p + q + 1
n.
Let
Kp
(resp. Kq) denote
the
complete
graph
on the set P (resp. Q). Set t pq
p2
+ 1. Consider
the
following inequality, denoted as (Kel
n
(p)
f x
:::;
0 :
t)
:E
Xin
+ t
I>in
:::;
o.
iEQ
iEP
The
following
can
be found
in
Deza
and
Laurent
[1992aJ.
Proposition
30.5.5.
For n
2:
5,
the inequality (Kel
n
(p)) T x
:::;
0 is valid
for
CUT
n
. I
It
is
an
open
question
to
determine
what
are
the
parameters
p
and
n for
which
the
inequality (Keln(p))T x
:::;
0 is facet inducing. Here
is
some
partial
information.
Proposition
30.5.6.
Assume
n
2:
7.
Then,
(i) The inequality (Kel
n
(2))T x
:::;
0 coincides (up to permutation) with the
clique-web inequality
CW~(
n -
4,
2, 2,
-1,
...
,
_l)T
x
:::;
0; hence,
it
is facet
inducing for
CUT
n
.
(ii) The inequality
(Keln(n
dimension
G)
3.
3))T x
:::;
0 defines a simplex face
of
CUTn
of
I
30.6
Complete
Description
of
CUTn
and
CUT~
for
n
~
7.
We
present here
the
complete linear description
2
of the
cut
cone
CUTn
and
the
cut
polytope
CUT~
for n
:::;
7.
For n =
3,4,
the
only facet defining inequalities for
CUTn
are
the
triangle
inequalities, i.e.,
Xij
XiI<;
Xjl<;:::;
0
for
distinct
i,j,k
in
{l,
...
,n}.
Hence, CUT3 (resp.
CUT~)
has
3 (resp. 4)
facets, while
CUT
4
(resp.
CUT~)
has
12
(resp. 16) facets.
For
n = 5,
the
facets
of
CUT
5
are,
up
to
permutation
and
switching, induced
by one
of
the
following inequalities:
2This
linear
description was
obtained
independently
by
several
authors.
In
particular,
the
linear
description
of
CUTs
was
obtained
by
Deza [1960, 1973aj, Davidson [1969];
that
of
CUTa
by
Baranovskii
[1971],
McRae
and
Davidson [1972], Avis [1989];
and
that
of
CUT,
by
Gr-
ishukhin
[1990].
In
fact,
McRae
and
Davidson
[1972]
had
already found
the
list of facets for
CUT
7
and
conjectured
that
it
was complete.

504
Chapter
30.
Other
Valid Inequalities
and
Facets
1.
Q5(1,
1,
-1,0,
of
x:::;
0 (triangle inequality),
2.
Q5(1,
1, 1,
-1,
-If
x:::;
0 (pentagonal inequality).
In
total,
CUT5 (resp.
CUT~)
has
30+10=40
facets (resp.
40+16=56
facets).
For
n =
6,
the
facets
of
CUT6 are,
up
to
permutation
and
switching,
induced
by
one of
the
following inequalities:
1.
Q6(1,
1,
-1,0,0,
of
x:::;
0,
2.
Q6(1,1,1,-I,-I,ofx:::;
0,
3.
Q6(2,
1,
1,
-1, -1,
-If
x:::;
o.
In
total,
CUT6 has
60+60+90=210
facets
and
CUT~
has
80+96+192=368
facets.
For
n =
7,
the
facets
of
CUT7 are,
up
to
permutation
and
switching,
induced
by one of
the
following eleven inequalities:
1.
Q7(1,
1,
-1,
0, 0,
0,
of
x:::;
0,
2.
Q7(1,
1, 1,
-1,
-1,0,
of
x:::;
0,
3.
Q7(2,
1,
1,
-1, -1,
-1,
of
x:::;
0,
4.
Q7(1,
1,
1,
1,
-1,
-1,
-If
x:::;
0,
5.
Q7(2,
2,1,
-1, -1,
-1,
-If
x:::;
0,
6.
Q7(3,
1, 1,
-1, -1,
-1,
-If
x:::;
0,
7.
CW~(1,
1, 1, 1, 1,
-1,
-If
x:::;
0,
8.
CW~(2,
2,
1, 1,
-1, -1,
-If
x:::;
0,
9.
CW~(3,
2, 2,
-1,
-1, -1,
-If
x:::;
0,
10. (Par7 f x
:::;
0,
11.
(Gr7fx:::;
O.
Among
the
11
types of facets of
CUT
7
,
the
first
five
are not simplices,
the
last
five are
not
hypermetric,
and
five
of
them
are
pure
(i.e., have all
their
coefficients
equal to
0,1,
-1)
(namely,
the
1
s
t,
2
nd
,4
t
h,
7th
and
10
th
ones).
Let
Fi
denote
the
facet
of
CUT7 defined by
the
i-th
inequality, for i =
1,
...
,11.
It
has been
computed
in Deza
and
Laurent
[1992c]
that
the
orbit
n(Fi)
(which consists of all
the
facets of CUT7
that
can
be
obtained
from Fi
by (root) switching
and/or
permutation)
contains, respectively, 105, 210, 630,
35, 546, 147, 5292, 8820, 2205, 7560,
and
13230 elements, for i =
1,
...
,11.
Hence,
among
the
11
types
of
facets
of
CUT
7
,
the
facet defined by
the
inequality
(Gr7 f x
:::;
0
is
the
one
that
has
the
largest
number
of distinct
permutations
and
switchings,
namely
it has 13230
ones!
30.6 Complete Description for n
::s:
7
505
Therefore, CUT7 has
IO(Fi)1
105
+ 210 + ... + 13230 38780 facets.
Using
Lemma
26.3.11, one can compute
that
CUT~
has 116764 facets.
The
number
of distinct (up to
permutation)
facets of CUT7 has been com-
puted
in
De Simone, Deza
and
Laurent [1994];
it
is equal to 36. More pre-
cisely, let
V(Fi) denote
the
number
of (root) switchings of
Fi
that
are pair-
wise
not
permutation
equivalent. For instance,
v(F
1
)
1 as any two (root)
switchings of
the
triangle inequality is again a triangle inequality.
In
fact,
V(Fi) =
1,1,2,1,3,2,4,7,5,3,7,
respectively, for i
1,
...
,11.
The
distinct
switchings of each
Fi
are described in detail in De Simone, Deza
and
Laurent
[1994].
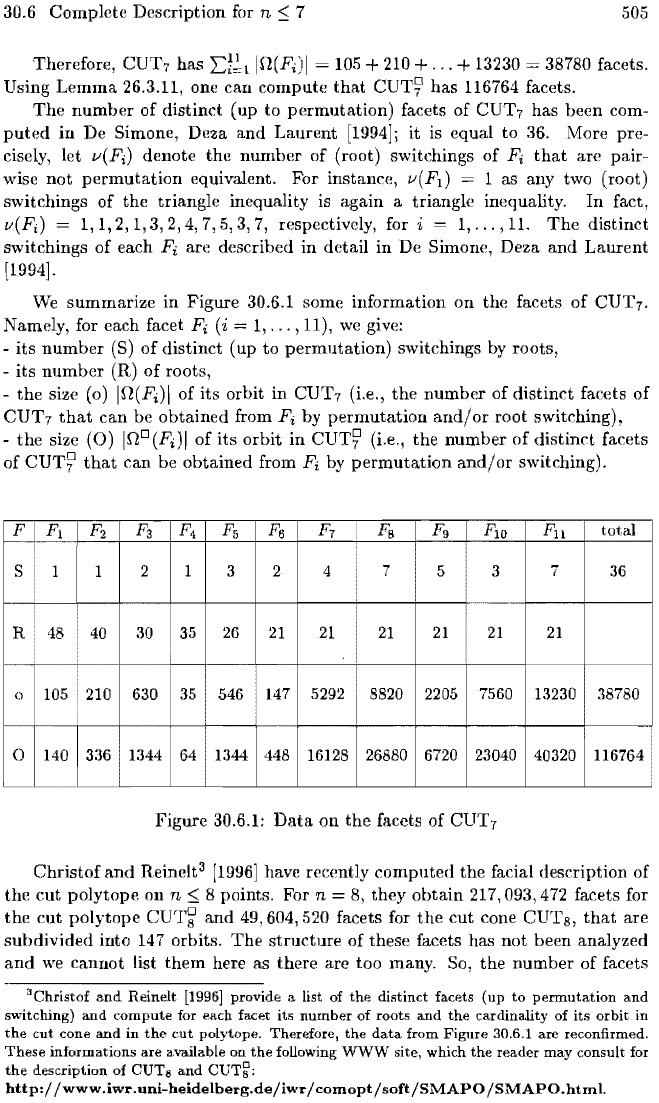
We
summarize
in Figure 30.6.1 some information
on
the facets
of
CUT7.
Namely, for each facet
Fi
(i =
1,
...
, 11),
we
give:
its
number
(S)
of
distinct (up to permutation) switchings by roots,
-
its
number
(R)
of
roots,
-
the
size
(0)
IO(F;)1
of its orbit in CUT7 (i.e.,
the
number
of distinct facets
of
CUT
7
that
can
be obtained from
Fi
by
permutation
and/or
root switching),
-
the
size
(0)
IOD(Fi)1
of its orbit
in
CUT~
(i.e.,
the
number
of
distinct facets
of
CUT~
that
can be obtained from
Fi
by
permutation
and/or
switching).
F7
Fs
F9
FlO
Fll
S 2 4 7 5 3 7 36
R484030
21 21
21 21
o 105 210 630 35
2205 7560
13230
38780
o 140 336 1344 64 23040
40320 116764
30.6.1:
Data
on
the
facets of
CUT
7
Christof
and
Reinelt
3
[1996]
have recently computed
the
facial description of
the
cut
polytope on n 8 points. For n =
8,
they
obtain
217,093,472 facets for
the
cut
polytope
and
49,604,520 facets for
the
cut
cone
CUT
8
,
that
are
subdivided into
147 orbits.
The
structure
of these facets has not been analyzed
and
we
cannot list
them
here as there are too many. So,
the
number of facets
JI"1h.;".~~
and
Reinelt
[1996] provide a
list
of
the
distinct
facets
(up
to
permutation
and
switching)
and
compute
for
each
facet
its
number
of
roots
and
the
cardinality
of
its
orbit
in
the
cut
cone
and
in
the
cut
polytope.
Therefore,
the
data
from
Figure
30.6.1
are
reconfirmed.
These
informations
are
available
on
the
following
WWW
site,
which
the
reader
may
consult
for
the
description
of
CUTs
and
CUT~:
http://www.iwr.uni-heidelberg.de/iwr/comopt/soft/SMAPO/SMAPO.htm!.

506
Chapter
30.
Other
Valid Inequalities
and
Facets
grows
dramatically
fast from n = 7
to
n =
8;
CUT~
has more
than
thousand
times
more facets
than
CUT~
!
This
is
an
indication
that
the
structure
of
the
facets
of
CUT
n is becoming more
and
more complicated
with
increasing values
of
n.
Inequalities
have
no
apparent
symmetries
and
are seemingly very difficult
to
generalize.
In
fact,
the
facet (Gr7)T x
:s
0 (from (5.9)) is
the
smallest
(and
unique
for n
:S
7)
example
of
a facet for which
we
could
not
find a
proper
generalization.
This
phenomenon
of
increasing complexity
of
the
facial
structure
for large n is
general for
polytopes
arising from
hard
optimization
problems.
For
instance,
the
facial
structure
of
the
symmetric
traveling
salesman
polytope
is
known
for n = 8
(Boyd
and
Cunningham
[1991], Christof,
Junger
and
Reinelt [1991]);
it
has
been
recently
computed
for n =
9,10
by
Padberg
[1995]
and
by
Christof
and
Reinelt
[1996].
(There
are 42,104,442 facets for n = 9
and
more
than
51,043,900,866
facets for
n = 10.)
30.7
Additional
Notes
We
mention
here some
other
interesting
questions
related
to
the
study
of
the
facets
of
the
cut
cone.
First,
we
consider some subcones
of
CUTn
generated
by
subfamilies
of
cuts;
we
show
that
they
inherit,
in
a sense, all
the
facets
of
CUT
n'
Then,
we consider
the
following
three
questions
related
to
the
collapsing
operation
in
the
cut
cone: Does every facet collapse
to
some triangle facet ?
Does every
(nonpure)
facet arise as collapsing
of
some
pure
facet?
Does every
facet have
the
parity
property?
Transport
of
Facets
to
Other
Subcones.
Let
K be a
subset
of
the
set
of
all
cut
vectors
in
Kn.
One
may
also
be
interested
in
finding
the
facial
structure
of
the
cone
~
(K)
or of
the
polytope
Conv(K) for some specific
cut
families
K. A general
problem
is as follows:
Which
facets
of
the
cut
cone
CUTn
do
the
polyhedra
~
(K)
and
Conv(K)
inherit?
Clearly,
any
inequality
which is facet
inducing
for
CUTn
is valid for
~(K)
and
Conv(K),
but
when
does
it
induce a
facet
of
the
latter
polyhedra?
Such
a
question
has
been
looked
at
in
the
case
when
K consists
of
the
even
cut
vectors, or
of
the
inequicut
vectors,
or of
the
equicut
vectors. A
surprising
feature
of
the
even
cut
and
inequicut
cones
ECUT
n
,
ICUT
n
,
and
of
the
equicut
polytope
EQCUT
n
is
that
they
already "contain" all
the
facets
of
the
cut
cone. More precisely, every inequality defining a facet
of
the
cut
cone
CUTn
can
be zero-lifted
to
some facet
of
ECUT
m
,
ICUT
m
,
EQCUT;;"
for
any
m large enough.
The
assertion (i)
in
Theorem
30.7.1 below is proved
in
Deza
and
Laurent
[1993b]
and
(ii), (iii)
in
Deza,
Fukuda
and
Laurent
[1993].
Theorem
30.1.1.
Given v E
jREn,
integers m
:::::
n,
define
v'
E
jR(';')
by
setting
vi
j
=
Vij
for
1
:S
i < j
:S
nand
vi
j
= 0 for 1
:S
i
:S
n < j
:S
m and
n
+ 1
:S
i < j
:S
m.
Assume
that the inequality v
T
x
:S
0 defines a facet
of
the
cut
cone
CUT
n
.
Then,
(i) The inequality
(v'l
x
:S
0 defines a facet
of
the even cut cone
ECUT
m
for
any m even, m
:::::
n +
5.

30.7
Additional
Notes
507
(ii) The inequality
(v')T
x
50
defines a facet
of
the inequicut cone
ICUT
m
for
any
m such that n <
(iii) The inequality
(v'f
x 5 0 defines a facet
of
the equicut polytope EQCUT;;,
for any
m odd, m
::::
2n
+ 1. I
The
valid inequalities
of
the
cut
cone
CUTn
can
also
be
transported
to
the
k-uniform
cut
cone
UCUT~
in
the
following
way.
Suppose
that
15k
5 n - 1,
k #
~.
Given v E , define
v*
E
litE
..
by
setting
v
T
6(
{n
+ I})
(n
-
k)(n
-
2k)
for 1 5 i < j 5 n.
If
the inequality v
T
x 5 0 is valid for
the
cut
cone
CUTn+l,
then
the inequality (v*)T x
50
is valid for
the
k-uniform
cut
cone
UCUT~
(Deza
and
Laurent
[1992e]). For example, for 1 5 i < j 5
n,
if
v
T
x
:=
x;,n+l - Xj,n+l -
Xij
50
is a triangle inequality,
then
(v*)T x 5 0 is
L (Xih - Xjh) -
(n
- 2k)Xij 5
o.
l$.h$n,hcl
i
,j
If
v
T
X Xij Xi,n+l Xj,n+l,
then
(v*)T x 5 0 is
2 L
Xhl
(n
-
k)
L (Xih + Xjh) +
(n
-
k)(n
- 2k - 2)Xij 5
O.
l$h$l$n
l$h$n,h¥i,j
In
fact,
the
2-uniform
cut
cone
UCUT~
is a simplex cone, which
is
completely
described by the
latter
G)
inequalities (Deza,
Fukuda
and
Laurent
[1993]).
Questions
Related
to
the
Collapsing
Operation.
We
address now
the
fol-
lowing
three
questions
about
the
facets of CUTn:
Question
1: Does every facet of
the
cut
cone collapse
to
some triangle
facet?
Question
2: Does every (nonpure) facet arise as collapsing of some
pure
facet?
Question
3:
If
the
inequality v
T
x 5 0 defines a facet of
CUT
n
,
is
it
the
case
that
v
T
6(
S)
is
an
even
number
for every
cut
vector
6(
S)
?
Recall
that
the
collapsing
operation
preserves valid inequalities
but
not
nec-
essarly facets. Call a facet tight
if
none
of
its collapsings is facet inducing. Hence,
the
answer to
Question
1
is
"yes" precisely if
the
only tight facet
of
the
cut
cone
CUTn
(for
any
n) is
the
triangle facet. A probably more reasonable conjecture
is
the
following:
The
number
of
tight facets
of
the
cut
cone is finite.
We
have checked
that
most
of
the
known classes
of
facets
of
CUT
n do indeed
collapse to some triangle facet. (As
an
example, let us consider
the
pure
c1ique-
web inequality;
(CW~)T
x 5
0;
the
inequality
obtained
from
it
by
collapsing all
the
nodes from
the
set
{I,
...
,
n}
\
{I,
r +
2}
into a single node, say 7t, is precisely
the
triangle inequality Xl,r+2
Xl
u
X
u
,r+2
5 0.)
In
fact,
there
are
often
several
ways of collapsing a given facet to some triangle facet. Collapsings to some

508
Chapter
30.
Other
Valid Inequalities
and
Facets
triangle
facet are given explicitly for all
the
facets of
CUT
7
in
De Simone, Deza
and
Laurent
[1994].
Given
a facet
inducing
inequality
v
T
x
:::;
0,
a purification of
it
is
any
pure
inequality
valid for a larger
cut
cone
and
admitting
a collapsing which is precisely
v
T
x
:::;
o.
As observed
in
De Simone [1992],
such
a purification always exists.
But,
Question
2 asks
whether
every facet
admits
a purification which is facet
inducing.
The
answer is "yes", by construction, for
the
class of clique-web facets.
Also,
in
Section 30.5,
we
mentioned
explicitly
the
inequality (30.5.2), which is
a
purification
of
the
nonpure
inequality (30.5.1). However, we do
not
know
the
answer
to
Question
2 for
the
classes
of
suspended-tree
inequalities, or of
path-
block-cycle inequalities.
It
is a challenging
problem
to
find some large class of
pure
facets from which
the
facets (30.1.1),(30.1.7),(30.1.8), or (30.1.11) could
be
deduced
by collapsing (recall
the
remark
preceding
Proposition
30.1.3).
If
the
answer
to
Question
3 is "yes",
we
say
that
the
inequality v
T
x
:::;
0
has
the
parity
property. We also say
that
the
vector v has
the
parity
property
if
v
T
8(5) is even for all
cut
vectors 8(5).
Let
eij
(1
:::;
i < j
:::;
n)
denote
the
coordinate
vectors in
:rm.
En
.
It
can
be
easily checked
that
v E
:rm.
En
has
the
parity
property
if
and
only
if
v
can
be
written
as
an
integer
combination
of
the
triangle
vectors
eij
+ eik +
ejk
(for 1
:::;
i < j < k
:::;
n)
and
of
the
double edge vectors
2eij
(for 1
:::;
i < j
:::;
n),
i.e., if
v E
Z(eij
+ eik +
ejk
(1
:::;
i < j < k
:::;
n),
2eij
(1:::;
i < j
:::;
n)).
Observe
that
the
parity
property
is preserved
under
switching
and
collapsing.
We have checked
that
every known class
of
facets
of
the
cut
cone enjoys
the
parity
property.
It
is
an
interesting
problem
to
look for a facet of
CUT~
that
does
not
have
the
parity
property;
a good
candidate
would
be
some inequality of
the
form
v
T
x
:=
L
Xij
:::;
va,
ijEE
where
E is
the
edge set of a regular
graph
of
odd
degree
and
Va
is
the
maximum
size
of
a
cut
in
the
graph.
(Note
that
both
assumptions
of validity
and
full
rank
are
necessary for
the
parity
property. Indeed,
it
is easy
to
construct
some valid
inequality
which is
not
facet
inducing
and
does
not
have
the
parity
property, or
some
nonvalid inequality whose set of
roots
has
full
rank
and
which does
not
have
the
parity
property.)
As
an
illustration,
we describe below
the
explicit
decomposition
of
some facet
defining inequalities
in
the
lattice
Z(
eij
+ eik +
ejk
(1
:::;
i < j < k
:::;
n),
2eij
(1
:::;
i < j
:::;
n)). We set
T(i,j;
k)
:=
Xij
-
xik
-
Xjk·
• For
the
facet defined
by
the
parachute
inequality: (Par2k+l)T x
:::;
0 (k
odd),
(Par2k+l)T x = L (T(i, i + 1; ai')
+T(i',
(i + 1)'; ai))
+T(l,
I';
0)
-T(k,
k'; 0),
l~i~k-l
