Deza M.M., Laurent M. Geometry of Cuts and Metrics

468

Chapter

29. Clique-Web Inequalities

antiweb

AW~.

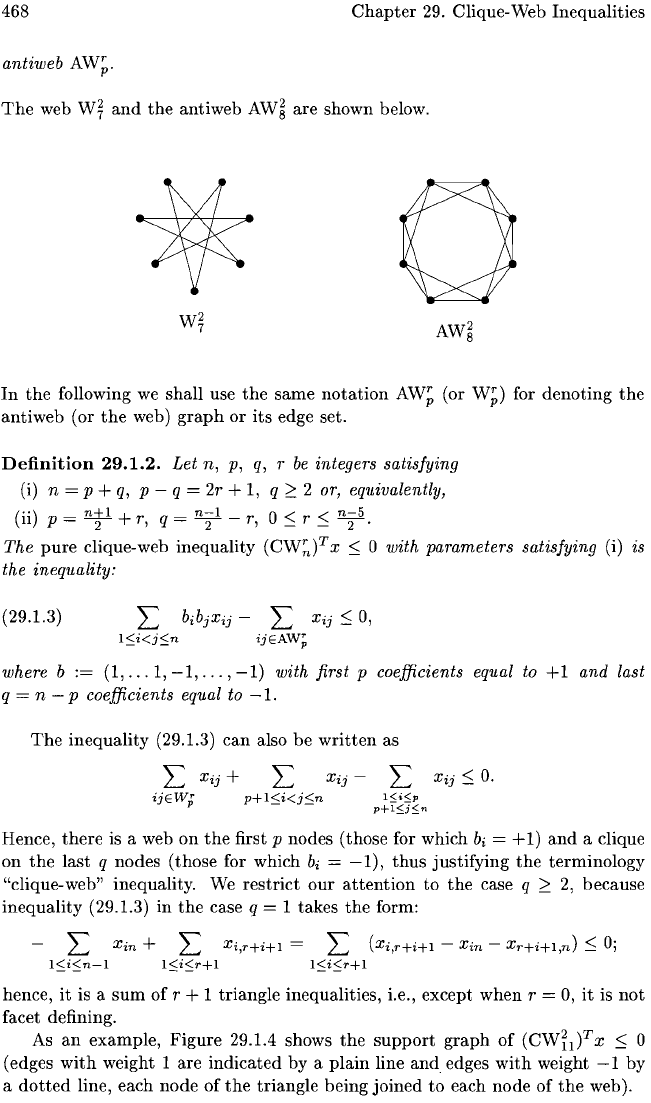
The

web

W~

and

the

antiweb

AW§

are shown below.

AW§

In the following

we

shall use

the

same

notation

AW~

(or

W~)

for denoting

the

antiweb (or

the

web)

graph

or

its

edge set.

Definition

29.1.2.

Let

n,

p,

q,

r

be

integers satisfying

(i)

n = p +

q,

p - q = 2r + 1,

q::::

2 or, equivalently,

(ii) p =

nt

1

+ r, q =

n;-1

-

r,

0::::;

r

::::;

n;-5.

The

pure

clique-web inequality

(CW~)T

x

::::;

0 with parameters satisfying (i) is

the inequality:

(29.1.3)

L bibjXij - L

Xij::::;

0,

where b

.-

(1,

...

1,

-1,

...

,

-1)

with first p coefficients equal to

+1

and last

q

= n - p coefficients equal to

-1.

The

inequality (29.1.3)

can

also be

written

as

L

Xij+

L

Xij-

ijEW;

p+1:'Oi<j:'On

L

Xij::::;

O.

l<i<p

p+l~j~n

Hence,

there

is a web

on

the

first p nodes (those for which

bi

= +

1)

and

a clique

on

the

last

q nodes (those for which

bi

=

-1),

thus

justifying

the

terminology

"clique-web" inequality. We

restrict

our

attention

to

the

case q

::::

2,

because

inequality (29.1.3) in

the

case q = 1 takes

the

form:

L

Xin

+ L

Xi,r+i+1

= L

(Xi,r+i+1

-

Xin

- X

r

+i+1,n)

::::;

0;

19:'On-1

1:'Oi:'Or+1

hence,

it

is a

sum

of

r + 1 triangle inequalities, i.e., except

when

r =

0,

it

is

not

facet defining.

As

an

example, Figure 29.1.4 shows

the

support

graph

of

(CWi1)T

x

::::;

0

(edges

with

weight 1 are indicated by a

plain

line

and

edges

with

weight

-1

by

a

dotted

line, each node

of

the

triangle being joined

to

each node

of

the

web).

29.1

Pure

Clique-Web Inequalities

469

Note

that

switching

the

inequality

(CW~)T

x

~

0 by

the

cut

o(

{I,

2,

...

p})

yields

the

following inequality:

(29.1.5)

((CW~)8({1,···,p})f

x:=

L

Xij+

L

Xij+

L

ijEW;

p+l:<;i<j:<;n

l<i<p

p+l:sj:Sn

Xij

~

pq.

In

the

case when q = 2 (i.e., r = n

2

5,

p = 2r + 3),

the

inequality (29.1.5)

is

also

called a

bicycle odd wheel inequality;

it

was introduced by

Barahona,

Grotschel

and

Mahjoub

[1985]

and

Barahona

and

Mahjoub

[1986]. Note

that

the

web

W

2r

+

3

is a circuit. Figure 29.1.6 shows

the

graph

supporting

the

bicycle

odd

wheel inequality

on

7 points, i.e.,

the

inequality (29.1.5) for n =

2r+5

and

r =

1.

Figure

29.1.6:

The

bicycle

odd

wheel inequality

on

7

points

Let us examine some special cases

of

the

clique-web inequality

(CW~f

x

~

o.

• For r =

0,

the

antiweb

AWg

is

the

empty

graph. Therefore,

the

clique-web

inequality

(CW~)T

x

~

0 coincides

with

the

pure

hypermetric

inequality.

• For

r =

1,

the

antiweb

AW~

is

a circuit.

The

clique-web inequality

(CW~)T

x

~

0

is

the

inequality (29.0.1), which was introduced

in

Deza

and

Laurent

[1992a]

under

the

name

of "cycle

inequality".

• For r = n

2

5

(the

largest possible value of

r),

i.e., p = 2r + 3, or q =

2,

the

web W;r+3 is a circuit.

The

clique-web inequality (CW;'.+5)T x

~

0

coincides (up to switching) with

the

bicycle

odd

wheel inequality.

Actually,

it

is

the

inspection

of

the

above

three

cases

that

led us

in

Deza

and

Laurent

[1992a]

to

the

general definition

of

the

clique-web inequalities.

470

Chapter

29. Clique-Web Inequalities

29.2

General

Clique-Web

Inequalities

In

order

to define the clique-web inequality

CW~(b)T

x::; 0 for an

arbitrary

vector

bE

zn,

we

have

to

use the collapsing operation (described in Section 26.4).

Let b =

(b

l

,

...

b

n

) be such

that

b;

2r + 1

and

suppose

that

for some 2

::;

p

::;

n 1. Set N

Ib;1

and

P

:=

Lf=1

bi

=

L;jb,>O

b

i

•

Let

1f(b)

denote

the

partition

of V N {I,

2,

...

,N}

into

the

following n classes:

the

p intervals

10

=

[1,

bll and Ii

[b

i

+ ... +

bi

+

1,

bl

+ ... +

b;

+ bi+d for

i =

1,

...

,p

- 1 (which

partition

[1,

PJ) together with n p

arbitrary

subsets

forming a

partition

of

the

set

[P

+

1,

N]

V;v

\

[1,

Pj

and

with respective sizes

Ibp+ll,·· ·Ibnl·

Definition

29.2.1.

Given integers b

(bl"

..

b

n

),

r

2:

0, such that L7=1

bi

=

2r + 1 and setting N

:=

Ll<i<n

Ibil,

the

clique-web inequality

CW~(b)T

x

~

0

is

defined

as

the Jr(b)-collapse-ol the (pure) clique-web inequality (CWN)T x

~

o.

The

clique-web inequality

CW~(b)T

x

::;

0

can

be described in a more ex-

plicit way using

the

notion

of

weighted antiweb. A weighted antiweb is

an

edge

weighted

graph

obtained by collapsing

of

a (usual) antiweb. Let b

l

,

...

b

p

be

positive integers such

that

Lf=l

b;

2:

2r + 1. Set P

bi

and

consider

the

partition

1fO(bb'" ,b

p

) of Vp =

{I,

...

,P}

into the p intervals

Io,h,

...

,Ip

described above.

Definition

29.2.2.

With the

above

notation, the antiweb

AW~(bl"

.,

b

p

)

is

the

weighted graph obtained

by

Jro(bl,

...

bp)-collapsing the antiweb

AW

p

.

Then

the clique-web inequality

CW~(b)T

x::; 0 can

be

alternatively described

as follows:

(29.2.3)

Xij

~

O.

l:::;i<jS;n

In

relation (29.2.3), the quantity LijEAW;(bl,

..

"b

p

)

Xij

should be understood as

the

sum

VijX,j,

where v denotes the edgeweight vector of

AW~(bl""

b

p

).

In

the pure case, i.e., when

Ib;1

= 1 for all i,

then

the

inequalities (29.1.3)

and

(29.2.3) coincide, i.e.,

CW~(I,

...

1,

-1,

..

, -

I)T

X

::;

0 and

(CW~?

x

~

0

coincide.

Let us give some examples of weighted antiwebs.

Lemma29.2.4.

A.ssume

bi

2:

r

fori

= 1,

...

,po

Then, the antiweb

AW;(bl,'"

b

p

)

,

r(r+l)

'W

l

'

't'

th '

't

G(1 2 ) 'th ' ht

r(r+I)

't

d I

'LS

2

.~

p,z.e.,z

zs

eczrcm "

...

p

wz

wezg

2

onzsege.s.

29.2

General

Clique-Web Inequalities

471

Lemma

29.2.5.

The

antiweb AW;(2,

1,

...

,1)

is the weighted graph

obtained

from

AW;

by

(i)

deleting the edges (p - i, T - i)

fOT

i = 0, 1,

...

,T

- 2,

and

(ii)

assigning

weight 2 to the edges

(1,i)

and

(1,p

- T + i)

fOT

i =

2,

...

,T.

I

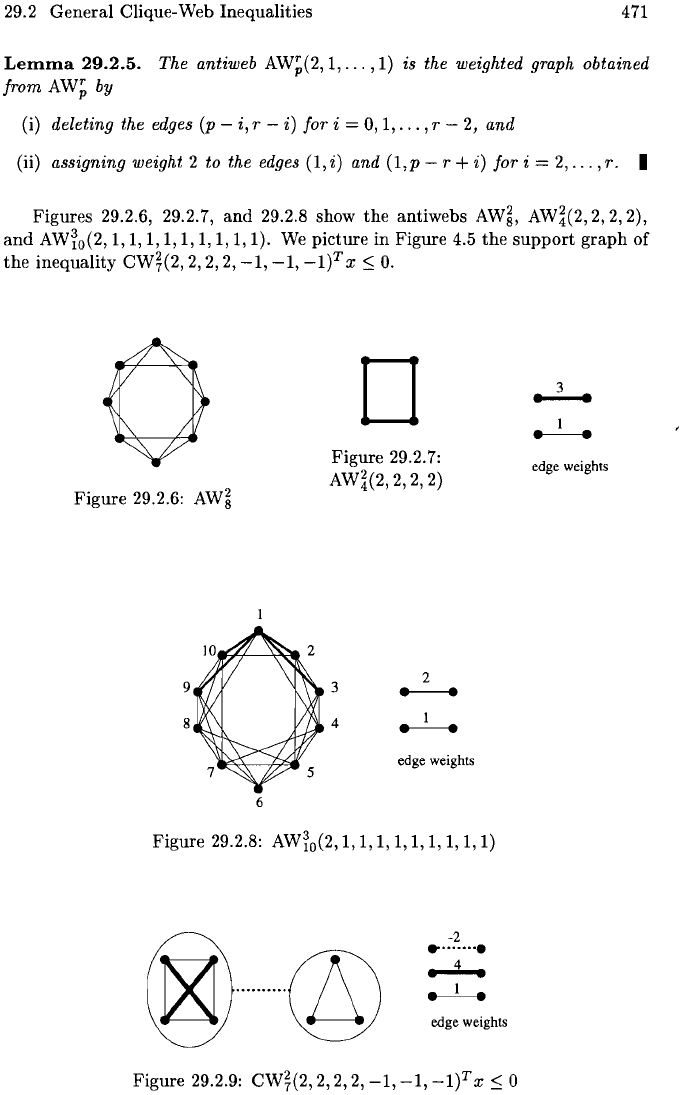
Figures 29.2.6, 29.2.7,

and

29.2.8 show

the

antiwebs

AW~,

AW~(2,

2,

2),

and

AWro(2, 1,

1,

1, 1, 1,

1,

1). We picture

in

Figure 4.5

the

support

graph

of

the

inequality

CW¥(2,

2,

2, 2,

-1,

_1)T x

:s;

O.

Figure

29.2.6:

AW~

9

6

o

Figure 29.2.7:

AW~(2,

2, 2,

2)

3

4

2

e------e

I

e------e

edge weights

Figure 29.2.8: AWro(2, 1, 1, 1,

1,

1,1,1,1)

@

........

@

-2

..........

~

.-!--.

edge weights

Figure 29.2.9: CW¥(2,

2, 2, 2,

-1,

_1)T x

:s;

0

edge weights

472

Chapter

29. Clique-Web Inequalities

29.3

Clique-

Web

Inequalities:

Validity

and

Roots

In

this

section, we show

that

the

clique-web inequality

CW~(b)Tx

::;

0 is valid

for

the

cut

cone

CUT

n'

Since the clique-web inequality

CW~

(b)T x

::;

0 is defined

as collapsing

of

a

pure

clique-web inequality

(CW~v)T

x

::;

0

(N

= L Ibi!),

it

is sufficient

to

prove validity in

the

pure case (recall

Lemma

26.4.1).

We

also

describe

the

roots

of

the

pure

clique-web inequality. Validity

of

the

pure

clique-

web inequality was established by Alon

[1990]

and

the roots were described by

Deza

and

Laurent

[1992bJ.

Proposition

29.3.1.

Let

p, r

be

integers such

that

p

?:

2r +

3,

r

?:

1

and

let S

be

a

subset

of

{I,

...

,p}

of

cardinality s.

(i)

If

s

::;

r,

then

IOKp(S)

n

AW~I

?:

s(2r

+ 1 s), with equality

if

and

only

if

S induces a clique

in

AW~!

i.e.,

if

any two nodes

of

S are adjacent

in

the

graph

AW;.

(ii)

1fr

+

1::;

s::;

~,

then

IOKp(S)

nAw;1

?:

r(r

+ 1), with equality

if

and

only

if

S is an

interval

of

[1,

p],

i.

e.,

if

S {i, i +

1,

i +

2,

...

, i + s - I}

for

some

i E {I,

...

,p}

(the indices being taken modulo

p).

Proof.

The

proof

is by induction on P

?:

2r +

3.

Let us first prove

the

result for

P

= 2r +

3.

Then,

AW;

= Kp \ C, where C is

the

circuit

with

node set [l,pJ

and

with

edges the pairs (i, i + r +

1)

for i = 1,

...

,p, where

the

indices are

taken

modulo

Pi so, C = (1, r +

2,p,

r +

1,p

-

1,

r,p

-

2,

r

1,

...

,2,

r + 3). Let S

be

a

subset

of

{I,

...

,p}.

Then,

IOK,,(S)

n AW;I =

s(2r

+ 3 - s) -IOK,,(S) n

CI

?:

s(2r

+ 1

s),

since

IOK,,(S)

n

CI

::;

2s. Moreover,

the

equality;

IOKl'(S)

n AW;I

s(2r

+ 1 s)

holds if

and

only

if

IOK,,(S)

n

CI

=

28,

i.e.,

if

no two nodes

of

S are adjacent on

Ci

this

means

that

any two nodes

of

S are adjacent on AW;, i.e.,

that

S induces

a clique in

AW;.

When

r + 1

::;

s

::;

~,

i.e., 8 = r +

I,

it

is

easy

to

see

that

S

induces a clique

of

AW;

if

and

only

if

S is

an

interval. Hence, Proposition 29.3.1

holds

in

the

case P 2r + 3.

Let us now suppose

that

Proposition 29.3.1 holds for some given p

?:

2r +

3.

We

show

that

it also holds for p +

1.

We

first establish a connection between

the

graphs

AW;

and

AW;+l'

We

suppose

that

AW;

and

AW;+l

are defined,

respectively, on

the

node sets

{I,

2,

...

,p}

and

{I,

2,

...

,p,p+

I}

(with

the

nodes

being aTranged

in

that

cyclic order; so, the new node p + 1 is inserted between

the

two nodes p

and

1 on the circuit (1,2,

...

,p)).

Then,

•

The

edges belonging

to

AW~,

but

not to

AW;+l'

are

the

pairs

(i,p

r + i)

for

i 1,

2,

...

,r

.

•

The

edges belonging

to

AW~+l'

but

not to AW;, are

the

pairs

(i,p

+ 1)

and

(p

+

1,p

r + i) for i 1,2,

...

, r .

29.3 Validity

and

Roots

473

Take a

subset

S of

{I,

...

,p,p

+

I}

and

set T

:=

S \ {p +

I}.

Suppose

that

8

:=

lSI

::;

~.

In

order

to

make

the

notation

easier let us

denote

by v

the

incidence vector of

the

cut

8

Kp

+l

(S).

Then,

1

8

K

p

+l

(S) n

AW;+ll

=

18

Kp

(T) n AW;I + L

Vij

- L

Vij

after

setting

ijEAW;+l

\AW;

ijEAW;\AW;+1

=

18

Kp

(T) n AW;I + L

(Vi,p+l

+ Vp

+1,p-r+i

-

Vi,p-r+i)

l:'Oi:'Or

r

=

18

Kp

(T)

n AW;I + L

6i

2:

18

Kp

(T)

n AW;I,

i=l

6i

:=

Vi,p+1 + Vp

+1,p-r+i

-

Vi,p-r+i

for all i = 1,

...

,

r.

(Note

that

6i

2:

0 for all i, by

the

validity of

the

triangle

inequalities.) We

distinguish

two cases

depending

whether

the

node

p+

1 belongs

to

the

set

S or

not.

Case

1: p + 1 ¢

S,

i.e., S =

T.

Then,

by

the

induction

assumption,

the

inequalities from

Proposition

29.3.1 hold. We now consider

the

equality case.

Suppose

first

that

8

::;

rand

18Kp+l(S)

n

AW;+ll

= 8(2r + 1 - 8).

Then,

18Kp

(S) n AW;I = 8(2r + 1 -

8)

and

6i

= 0 for all i = 1,

...

,r.

By

the

induction

assumption,

the

set S induces a clique

in

AW;.

Then,

S also induces a clique

in

AW;+l'

Indeed,

suppose

that

there

exist

i,j

E S such

that

ij

¢

AW;+l'

Then,

ij

E

AW;

\

AW;+l

and,

thus,

ij

is of

the

form

(i,p-r+i)

for some i E

{I,

...

,r}.

This

implies

that

6i

= 2 (since p + 1 ¢

S),

yielding a

contradiction.

Suppose

now

that

r + 1::; 8::;

~

and

that

18Kp+l(S)

n AW;+l1 =

r(r

+

1).

Then,

18

Kp

(S) n AW;I =

r(r+

1)

and

6i

= 0 for all i =

1,

...

,r. By

the

induction

assumption,

the

set

S is

an

interval

in

[1,

pl.

If

the

pair

{I,

p} is

not

contained

in

S,

then

S is still

an

interval

in

[1,p

+

1].

Suppose

that

both

nodes

l,p

belong

to

S.

Then,

S =

[p

- x + 1,

p]

U

[1,

y]

for some integers x, y

2:

1

with

x + y

2:

r +

1.

If

x

2:

r,

then

p - r +

1,1

E S,

implying

that

61

=

2.

If

y

2:

r,

then

p,

rES,

implying

that

6

r

=

2.

If

x

::;

y

::;

r -

1,

then

p - x + 1,

xES,

implying

that

6

x

= 2

and,

finally,

if

y

::;

x

::;

r

-1,

then

p - y + 1,

yES

implying

that

6

y

=

2.

In

all cases, we

obtain

a contradiction. Therefore,

the

pair

{I,

p} is

not

contained

in S

and,

thus,

S is

an

interval in [1,p +

1].

Case

2: p + 1 E S; so,

ITI

= 8 -

1.

Suppose

first

that

8

::;

r. Denote by K

the

set

of

indices i E

[1,r]

for which

6i

= 0; set

k:=

IKI.

Then,

18

Kp

(T)

nAW;I2:

(8

- 1)(2r + 1 -

(8

- 1)) by

the

induction

assumption.

Moreover,

6i

= 2 for all

i E

[1,r]

\K.

As

Sn

{i,p

-

r+i}

=1=

0 for all i E K,

we

obtain

that

82:

1

+k.

Therefore,

18Kp+l

(S) n AW;+l1

2:

(8

- 1)(2r + 1 - (8 - 1)) + 2(r - k)

2:

(8

- 1)(2r + 1 - (8 - 1)) + 2(r - 8 +

1)

= 8(2r + 1 - 8).

This

shows

that

the

inequality from

Proposition

29.3.1 (i) holds.

Suppose

now

that

equality: 18Kp+,(S)nAW;+11 =

8(2r+I-8)

holds.

Then,

18Kp(T)nAW;1 =

474

Chapter

29.

Clique-Web Inequalities

(8

1)(2r + 1

(8

1)) and, thus, by the induction assumption, T induces a

clique

in

AW;. Moreover, 8 = 1 +

k.

This implies

that

15

n

{i,p

r +i}1 = 1 for

all

i E

K.

Therefore,

5n{i,p-r+i}

= 0

for

i E

[l,rJ\K

and

5n[r+1,p-rJ

=

0.

We

show

that

5 induces a clique in AW;+1' Note first

that

the node p + 1

is

adjacent

to

all other nodes from 5

in

AW;+l' Suppose

that

i

i-

j E 5 are not

adjacent in

AW;+l'

Then,

i,j

E T and, thus,

ij

is

an

edge from AW;+1

\AW;.

Hence, j p - r + i and, thus,

the

set 5 contains

both

nodes i and p - r + i,

yielding a contradiction.

Suppose now

that

8

~

r+2. Then,

It5

Kp

(T)nAW;1

~

r(r+l)

(by the induction

assumption, as

ITI

~

r + 1). Hence,

the

inequality from Proposition 29.3.1 (ii)

holds. Moreover, iflt5Kp+1(5)nAW;+l1 =

r(r+I),

then

It5

Kp

(T)nAW;1 =

r(r+l)

and

Ai

= 0 for all i E

[1,

r]. By the induction assumption,

the

set T is

an

interval

in

[l,p].

If

1 E 5 or if p E

5,

then

the

set 5 remains an interval in

[I,p

+

1].

Suppose

that

l,p

t/:

5.

Then, T

[x,V]

for some 2:::; x < V

:::;

p - 1. For each

i

E

[1,

r],

we

have

15

n

{i,p

r +

i}1

~

1 as

Ai

O.

Hence, r E 5 since p

t/:

5,

which implies

that

x

:::;

r. Moreover, p r +

x-I

E 5 since

x-I

t/:

5,

which

yields

p - r +

x-I:::;

V,

i.e.,

ITI

= - x + 1

~

P - r. Therefore, s

~

p - r +

1,

which contradicts the fact

that

s

:::;

Let us finally suppose

that

s r +

1.

Then,

16Kp(T)

n AW;I

~

r(r + 1) (by

the

induction assumption), implying

that

16Kp+l(5)

n AW;+ll

~

r{r + 1), i.e.,

the

inequality from Proposition 29.3.1 (ii) holds. Suppose now

that

16Kp+!

(5) n

AW;+l1 =

r{r+I).

Then, IOKp(T)nAW;1 =

r(r+l)

and

Ai

= 0 for all i E [I,r].

Therefore,

the

set T induces a clique in AW;. Moreover,

15n{i,p-r+i}1

= 1 for

all

i E

[1,

rJ

and

5 n

[r

+

I,p

rJ

0.

We

show

that

5

is

an

interval in [I,p + 1].

If

i,j

E

[1,

r]

are such

that

i E 5 and j

t/:

5,

then p - r + j E

5,

implying

that

j

~

i (as p - r + j should be adjacent

to

i in AW;). Hence, 5 n

[1,

rJ

is

of

the

form [l,x] for some 0:::; x

:::;

r. Therefore, 5 =

{p

+ I} U

[1,x]

U

[p

- r + x + l,p]

is

indeed

an

interval in

[I,p

+

1].

I

The

next results establish validity

of

the inequality

(CW~)T

x

:::;

0 and de-

scribe its roots. Given

n p + q with p q =

2r

+ 1

and

q

~

2,

the

clique-web

inequality

(CW~)T

x:::;

0

is

as defined

in

Definition 29.1.2.

Proposition

29.3.2. The clique-web inequality

(CW~)T

x < 0

i.q

11alid

for

CUT

n

·

Proposition

29.3.3. Assume r

~

1. The roots

of

(CW~)T

x

:::;

0

are

the cut

vectors

15(5)

where

5 = 5+

u5_

with

5+

~

{I,

2,

...

,p}

and

5_

~

{p+I,

...

,n}

and 5

is

of

one

of

the following

two

types:

(i) (type 1)

5_

0 and

5+

induces a clique in AW;.

(ii) (type

2)

5+

is

an

interval of[l,p] with

r+I

:::;

15+1

:::;

p-r

and

15+1-15_1

r,

r + 1.

Remark

29.3.4.

Recall

that,

when

we

say

that

5+

is

an

interval of [I,pj,

we

mean

that

5+

=

{i,i

+

1,

...

,i

+

15+1-

I} (for some i E {I,

...

,p}) where the

29.3 Validity

and

Roots 475

indices are taken modulo p. There are some redundancies in

the

presentation

of

the roots given

in

Proposition 29.3.3.

It

is easy

to

see

that

a nonredundant

description of the roots (Le., in which each root occurs exactly once) can

be

obtained by replacing in Proposition 29.3.3 the family

of

sets

of

type

2 by

the

family

of

sets of type 2' where

(type2')S+

is

an

interval

of[l,p]

withr+1:::;

IS+I:::;

:-.rote

also

that,

if S

s:;;

{I,

...

,p} induces a clique in AW;,

then

lSI:::; r + 1

holds. For example, the interval

[1,

r +

1]

{1,2

...

,r, r + I} induces a clique in

AW;i therefore, any subset

S of the following type

I'

induces a clique in AW;:

(type

1*)

S

is

contained in

an

interval

of

sizer

+ 1 of [l,pj.

In

general, there may exist

other

sets

than

those

of

type

1*

inducing a clique

in

AW;. For instance, for

'I'

3

and

p

9,

the set {I, 4,

7}

induces a clique in

AW~.

However, for p > 3k, the only sets inducing cliques in AW; are those of

type

1*.

Actually, in all our proofs for clique-web facets,

we

shall only use roots

15(S)

in

which S is

of

type

1*

or of

type

2.

I

Proof

of

Propositions 29.3.2 and 29.3.3. Take a subset S

of

{I,

...

,n}.

Then,

S =

S+

uS_,

where

s:;;

{I,

...

,p}

and

S_

s:;;

{p+

1,

...

,

n}.

Set s

:=

lSI,

s+

:=

IS+I,L:=

IS_I; so, s

s+

+L.

Then,

b(S)(2r + 1 - b(S))

I15KI'(S)

n AW;I

(s+

L)(2r

+ 1

(s+

L))

-115KI'(S) n AW;I.

Suppose

that

s+

:::;

r.

Then,

The

first inequality follows from Proposition 29.3.1 (i)

and

the second one from

the fact

that

the

mapping x

f-+

x(2r + 1 - x) is monotone nondecreasing for

x

:::;

r.

Therefore, if

15(S)

is a root of

(CW~)T

x

:::;

0,

then

L = 0 and, by

Proposition 29.3.1 (i),

S+

induces a clique in AW;. Suppose now

that

r + 1

:::;

8+

:::;

¥.

Then,

The

first inequality follows from Proposition 29.3.1 (ii)

and

the second one from

the

fact

that

x(2r + 1 - x)

:::;

1'(1'

+

1)

for any integer x. Therefore, if

15(S)

is a

root

of

(CW~)T

x

:::;

0,

then

s+

- L = r, r + 1 and,

by

Proposition 29.3.1 (ii),

S+

is

an

interval. This concludes the proof. I

How to find the roots of a general clique-web inequality

CW~(b)T

x

:::;

0 ?

They

can

be deduced from the roots in the pure case, in the manner described

in

Lemma

26.4.1 (ii). Let us, as

an

example, describe the roots of two clique-

web inequalities, namely,

of

CW~(b)T

x

:::;

0 where b

i

;::::

'I'

if

b;

> 0,

and

of

CW~(2,

1,

...

,1,

-1,

...

)

-1)T

x:::;

O.

476

Chapter

29.

Clique-Web Inequalities

Proposition

29.3.5.

Suppose

that

b;

2::

r

for

i E

{I,

...

,p}

and

b;

< 0

for

i E {p + 1,

...

, Then, the roots

of

CW~(b)T

x

~

0 are the

cut

vectors

8(S)

for

which S n

[1,p]

is

an

interval

of

[1,p]

and

b{S) = r, r +

1.

I

Proposition

29.3.6.

The roots

of

CW~

(2,

1,

...

,1,

-1,

...

,

_1)T

x

~

0 (where

there are p

1 coefficients + 1

and

n - p coefficients

-1)

are the

cut

vectors

8(S)

where S S+ U

S_

with

{I,

2,

...

,p}

and

S_

~

{p

+ 1,

...

,n}

satisfying

(i)

or

(ii).

(i)

S_

0,

1

'I.

S (resp. 1 E

S)

and

S (resp. S U

{p

+

I})

induces a

clique

in

AW~+I'

where AW;+1 is the antiweb defined

on

the p + 1 nodes

1,2,

...

,p,

p +

1,

taken

in

that

circular order.

(ii) is an

interval

of

[1,p]

and

either, 1'1. S+, r + I

~

IS+I

~

p + 1 -

rand

IS+I-IS-I = r, r + 1,

or, 1 E S+, r

~

IS+I

~

p -

rand

IS+I

-IS_I

= r, r - 1. I

In

the

case r = 1, A

W!

is

just

a circuit of length p

and

any interval collapsing

(i.e.,

we

collapse only consecutive nodes

on

the circuit)

of

a circuit is again a

circuit. Therefore, for

r = 1, the clique-web inequality

CW~(b)T

x

~

0 takes a

particularly

easy form; namely, if b

1

,

...

,b

p

> 0, b

p

+

1

,'"

,b

n

< 0,

then

CW~(bl

x

:=

L b;bjXij - ( L

Xi,i+l

+

XI

P

)

~

O.

1:Si<J'Sn

l'SiSp-1

In

particular,

for all roots

8(S)

of

CW~(bl

x

~

0,

S n

[1,p]

must

be

an

interval.

Observe also

that,

for any integers r

2::

1, b

1

,

...

, b

p

> 0 > b

p

+

l

,""

b

n

,

the

inequality

(29.3.7)

r(r+I)

( L )

".

b·b·x'·

-

X·

'+1

+

Xl

< 0

~

'J

2

','

p-

IS,<jSn

l'Si'Sp-1

is valid for

CUT

n

•

When

b

l

,

...

, b

p

2::

r,

as

we

noted in

Lemma

29.2.4,

the

clique-

web inequality

CW~

(b)T x

~

0 is indeed

of

the

form (29.3.7). However,

if

b;

< r

for some i E

{I,

...

,p},

then

the

inequality (29.3.7) is

not

facet inducing, since

it

is

dominated

by

CW~(bl

x

~

O.

(Indeed, one can easily check

that

nC[

holds for any subset S

of

{l,

...

,p}, where C denotes

the

circuit (1,2,

...

,p)

(using

the

definition

of

collapsing

and

decomposing S as a union of intervals

of

[1,p); see

Lemma

2.8 in Deza, Grotschel

and

Laurent [1992]).)

As

an

easy consequence

of

the

description of

the

roots

of

(CW~fr

x

~

0,

we

have

the

following result.

Proposition

29.3.8.

Assume

that

r

2::

1. Then,

b(S)

E

{I,

2,

...

,r

+ I}

for

every

nonzero root

8(S)

of

CW~(b)T

X

~

o.

I

29.4 Facets

477

29.4

Clique-

Web

Facets

In

this

section,

we

describe several classes

of

clique-web facets, Le., several classes

of

parameters

b for which

the

inequality

CW~(b)T

x SO is facet inducing.

The

full

characterization

of

all clique-web facets seems a very

hard

problem; actually,

this

problem

is

already

not

solved for

the

special case r = 0

of

the

hypermetric

inequalities. We

can

restrict

ourselves here to

the

case r

:2':

1,

since

the

case

r = 0

has

been

considered

in

the

preceding chapter.

The

following classes

of

clique-web facets are known:

•

(CW~)T

x S

0,

Le.,

CW~(I,

...

,

1,

-1,

...

,

_1)T

X S 0 (pure case),

•

CW~(r,

...

, r,

-1,

...

,

_1)T

X S 0 for r

:2':

1,

P:2':

5,

•

CW~(b1"'"

b

p

,

-1,

...

,

-ll

x S 0

with

b

1

,

•••

, b

p

:2':

r

and

some

additional

conditions (see

Theorem

29.4.4),

•

CW~(2,

1,

...

,1,

-1,

...

,

-1)Tx

S 0 for

r:2':

1,

P:2':

2r +

3,

•

CW~(b1"'"

b

p

,

-1,

...

,

-1,

-2

...

,

_2)T

X S 0 for b

1

,

...

, b

p

:2':

r

and

some

additional

conditions (see

Theorem

29.4.6).

Here are

three

examples

of

clique-web facets1

CW~(b

l x S 0

with

r =

1:

•

CWi(3,

2, 2,

-1, -1, -1,

_1)T

x S

0,

•

CWi(2,

2,

1, 1,

-1,

_1)T

x S

0,

•

CWi(l,

1,

1, 1,

-1,

_1)T

x S

O.

For n S 6, all

the

facets

of

CUT

n are hypermetric

and,

for n =

7,

the only clique-

web facets

of

CUT

7

are

either

hypermetric

or

one

of

the above

three

facets. See

Section 30.6 for a full description of

the

cut

cone

CUTn

for n S

7.

Let

us

start

with

mentioning a necessary condition for a clique-web inequal-

ity

CW~

(b)T x S 0 to

be

facet defining.

The

next result generalizes Proposi-

tion 28.2.1, which corresponds to

the

case r = 0

of

hypermetric inequalities.

Proposition

29.4.1.

Let

b E

zn

with

l:i=l

bi

= 2r + 1, r

:2':

1,

and

b

1

:2':

b

2

:2':

•..

:2':

b

p

> 0 >

bp+l

:2':

•.•

:2':

b

n

·

If

P

b

1

+ b

2

-

b

n

> L

bi

- r

i=l

then

the face F

of

CUTn

defined by the clique-web inequality

CW~(bl

x S 0 is

contained

in

the facet defined by the triangle inequality:

X12

-

Xln

-

X2n

S

0;

lThese

three

clique-web facets were discovered

by

Assouad

and

Delorme

[1982] (cf.

Assouad

[1984]).

In

fact,

the

first

one

had

also

been

found

earlier

by

Avis [1977]

and

(in

the

context

of

the

correlation

polytope)

by

McRae

and

Davidson

[1972].

These

facets

demonstrate

that

the

cut

cone

does

have

some

facets

that

are

not

induced

by

hypermetric

inequalities.

It

had,

indeed,

been

speculated

by

several

authors

at

various

moments

(e.g.,

by

Davidson

[1969],

Deza

[1973a]'

Pitowsky

[1991])

that

all facets

of

the

cut

cone

are

hypermetric.

Deza M.M., Laurent M. Geometry of Cuts and Metrics

Подождите немного. Документ загружается.