Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.


30.1 Suspended-Tree Inequalities
489
Then, the inequality (30.1.1) defines a facet
of
CUT
n
.
Proposition 30.1.3
and
Theorem 30.1.4 with the condition (i) are given in Boros
and Hammer
[1993); the alternative condition (ii) of Theorem 30.1.4 is proposed
in Boissin
[1994J.
The
results are presented there in the context of the correlation
polyhedra.
The
proof below is taken from Boros
and
Hammer [1993].
Proof.
We
show
that
the
inequality:
(30.1.5)
2:
PiJ)
2:
0,
ijEE(T)
which corresponds to the inequality (30.1.1) via
the
covariance mapping pointed
at
position
1,
defines a facet of
CORn-I-
b2,.'"
b
n
are integers such
that
b
2
,
•••
,b
p
2:
r,bp+ll
...
,b
n
-1,
T
is
a spanning tree on {2,
...
,p}
and
one
of
the
conditions (i),(ii)
of
Theorem 30.1.4 holds. Denote
the
inequality
(30.1.5) by v
T
P
2:
O.
Let w
T
P
2:
0 be a valid inequality for
CORn-l
such
that
{p
E
CORn-II
v
T
P
=
O}
<;;;
{p E
CORn-l
Iw
T
pO}.
We
show
that
w =
AV
for
some A
>
O.
Let S denote
the
family consisting
of
the sets 8
<;;;
{2,
...
, p} for which
the
subgraph
T[8)
of
T induced by 8 is connected
and
such
that
r + 1
:::;
b(8)
:::;
n - p + r + 1. For
io
E {p +
1,
...
,
n},
let
Sio
denote
the
family consisting of
the
sets 8 U
8',
where 8 E
Sand
8'
{p
+
1,
...
,
n}
\ {
io}
with
18'1
=
b(
8) - r 1.
Set
Sio
:=
{A
U {io} I A E Sio}.
We
prove an intermediary result.
Claim
30.1.6.
For each
io
E
{p
+
1,
...
,n},
the incidence vectors
of
the
mem-
bers
of
Sio
have rank n
2.
Proof
of
Claim 30.1.6.
We
show
that
the space consisting
of
the vectors
that
are
orthogonal to all incidence vectors
of
members
of
Sio
has dimension 1. Consider
the
vector y E
jRn-l
defined by
Yi
:=
bi
(i =
2,
...
,p), Yio
:=
-r
-
1,
and
Yi
:=
-1
(i E
{p
+
1,.
_ .
,n}
\ {io}). Clearly, Y is orthogonal to all incidence
vectors
of
members
of
Si
o
'
Let x E
jRn-1
such
that
Xio
= 0
and
x is orthogonal
to all incidence vectors
of
members
of
Si
o
'
We
show
that
x
O.
Let 8 E
S.
Then,
x(8)
+
x(8')
0 for every subset
8'
of
{p +
1,.
_.,
n}
\ {io} of cardinality
b(S) r
1.
Xi
a for i E
{p
+ 1,
...
,
n}
\ {io}, where
a:=
xeS)
b(S) - r
-1'
Therefore,
(a)
(x + ab)(8) =
a(r
+
1)
for all S E
S.
Suppose, first,
that
the condition (i) from Theorem 30.1.4 holds.
If
S E S
and
if
a node i E {2,
...
,p}
\ 8 is adjacent to a node of 8 in the tree
T,
then
8u
{i} still
belongs
to
S.
Hence,
Xi
+
ab;
= 0 by (a) and, therefore, this relation holds for

490
Chapter
30.
Other
Valid Inequalities and Facets
all i
E {2,
...
,p}
\
8.
Now, taking for 8 the two sets 8
1
and 8
2
from condition
(i),
we
deduce
that
Xi
+
ab
i
= 0 for all i E {2,
...
,p}.
This implies
that
X =
O.
Suppose
now
that
the condition
(ii)
from Theorem
30.1.4
holds. Let 8 be the
node set
ofapath
(i1,'"
,is) in T.
If
181
2 4,
then
all the sets
8,
8\{i
s
},'"
,8\
{is,
is-I,'"
,i3}, and
8\{id,
...
,8\{il,'"
,i
s
-2}
belong to
S.
Hence,
we
deduce
from (a)
that
Xi
+
ab
i
= 0 for all i E
8.
Therefore,
Xi
= 0 for all i E
8.
As
T
is
not a star, every node of T lies on a
path
of
length
at
least 4. This shows
that
X =
o.
I
Clearly, for
io
E
{p
+
1,
...
,
n}
and 8 U
8'
E Sio'
the
correlation vectors
Jr(8
U
8')
and Jr(8 U
8'
U {io}) are
both
roots of the inequality
(30.1.5).
Hence,
the
relations
Vio
+ L
Vi,io
= 0,
Wio
+ L
Wi,io
= 0
iESUS'
iESUS'
hold for all 8 U
8'
E Sio'
We
deduce from Claim
30.1.6
that
there exists a scalar
Aio
such
that
Wio
=
Ai
o
Vio
and
Wi,io
=
Aio
Vi,io
for all i E {2,
...
,
n}
\ {i
o
}.
As
Vij
-I-
0 for i, j E
{p
+
1,
...
,n},
we
obtain
that
all
Aio'S
are equal to, say,
A.
Hence,
Wi
=
AVi
for i = p + 1,
...
,n
and Wij =
AVij
if
at
least one of i, j belongs
to
{p
+ 1,
...
,n}.
Set U
:=
W - Av.
We
show
that
U =
O.
For
io
E {2,
...
,p},
let lio denote
the family consisting
of
the
nonempty sets 8
~
{2,
...
,p}
\ {i
o
} such
that
the
subgraphs T[8] and
T[8u{io}]
are
both
connected and
b(8)+b
io
:::;
n-p+r+
1.
Clearly, if 8 E lio and
8',
8"
~
{p+
1,
...
,n}
with
18'1
=
b(8)
-
r,
18"1
=
bio
-
1,
then
the correlation vectors
Jr(
8 U
8')
and
Jr(
8 U
{i
o
}
U
8'
U 8") are roots
of
the
inequality
(30.1.5).
This implies
that
(b)
Uio
+ L
Ui,io
= 0 for all 8 E
li
o
'
iES
If
i is a node
ofT
adjacent to io, then {i} belongs to lio and, thus,
Uio
+Ui,io =
o.
If
(io, i
l
,
...
, is)
is
a
path
in
T,
then
all sets
{id,
{iI, id, ...
,{il,"
.
,is}
belong
to
li
o
'
From (b),
we
deduce
that
Uio,i2
=
Uio.iJ
=
...
=
Uio,i,
=
O.
This shows
that
Uio,i
= 0 if i is not adjacent to
io
and
Uio,i
= -Uio if i
is
adjacent to
io.
Hence,
we
obtain
that,
for some a E
IR,
U2
=
...
= up =
a,
Uij
=
-a
if
ij
is
an
edge
of
T and
Uij
= 0 otherwise. Finally, a = 0, which shows
that
U = 0, i.e.,
W = Av. I
We
now present some other classes of facets, which are obtained by modifying
the
definition of the suspended-tree inequalities. Let b =
(b
l
,
...
, b
2p
+
l
)
with
bi
= 1
ifi
E {1,
...
,p+2}
and b
i
=
-1
ifi
E
{p+3,
...
,2p+l};
so,
E;~i1bi
= 3.
Let T be a spanning tree defined on the p + 1 nodes of
the
set {2,
...
,p
+ 2}.
Hence,
the
inequality:
:::;0

30.1 Suspended-Tree Inequalities
491
is
the
case b = (1,
...
,1,
-1,
...
,
-1)
and
r = 1
of
the
inequality (30.1.1). Con-
sider
the
following switching of it:
(30.1.7)
=p(p+1)-2.
Therefore, from
Theorem
30.1.4,
the
inequality (30.1.
7)
defines a facet
of
the
cut
polytope
CUT~P+l
if T is
not
a
star.
The
following two generalizations of
the
inequality (30.1.7) were proposed by De Souza
and
Laurent
[1995].
They
allow,
respectively,
the
tree
T
to
be defined on p or
on
p - 1 nodes
but,
in
order
to
preserve validity,
an
additional
term
(whose
support
graph
is K3 or K
5
)
must
be
added
to
(30.1.7); also
the
right
hand
side
has
to
be
modified.
Consider
the
complete
graph
K
2p
+
1
defined
on
the
nodes of
{I,
...
, 2p + I}.
Let
T be a
spanning
tree
defined
on
the
p nodes of {2,
...
,p+
I}
and
let
.6.
denote
the
complete
graph
K3 defined
on
{p +
2,p
+
3,p
+ 4}. Consider
the
inequality:
(30.1.8)
(We
remind
that
di
denotes
the
degree of node i in
the
tree
T.) For instance, let
p = 5
and
let T
be
the
tree from Figure 30.1.9.
Then,
the
quantity
pH
~)2
-
di)Xli
+ L
Xij
- L
Xij
is depicted in
Figure
30.1.10.
i=2
ijEE(T)
ijEA
Figure
30.1.9 Figure 30.1.10
:,/:~'\\
..........•
Suppose
now
that
T is a
spanning
tree
defined
on
the
p
-1
nodes of {2,
...
,
p}.
Let
0
denote
the
5-circuit (p +
1,p
+
2,p
+
3,p
+
4,p
+ 5)
and
let
0'
denote
the
5-circuit (p +
1,p
+
3,p
+
5,p
+
2,p
+ 4). Consider
the
inequality:
(30.1.11)
L
Xij-
ijE
K
2p+l
(
t(2
-
di)Xli
+ L
Xij
+ L
Xij
- L
Xij)
i=2
ijEE(T)
ijEC
ijEC'
:S
p(p
+ 1).
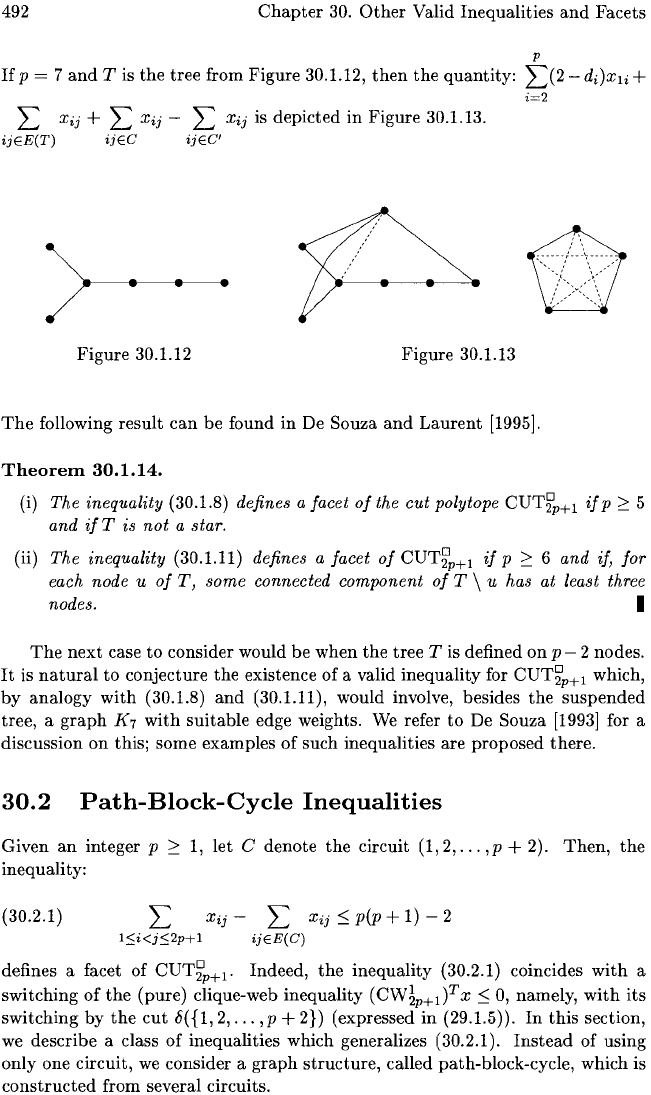
492
Chapter
30.
Other
Valid Inequalities
and
Facets
p
If
p = 7
and
T is
the
tree from Figure 30.1.12,
then
the
quantity:
2)2
-
di)xli
+
i=2
L
Xij
+ L
Xij
- L
Xij
is depicted
in
Figure 30.1.13.
ijEE(T)
ijEC
ijEC'
)---------------. . .
Figure
30.1.12 Figure 30.1.13
The
following result
can
be found
in
De Souza
and
Laurent
[1995].
Theorem
30.1.14.
(i) The inequality (30.1.8) defines a facet
of
the
cut
polytope
CUT~P+l
if
P
::::
5
and
if
T is
not
a star.
(ii) The inequality (30.1.11) defines a facet
of
CUT~P+l
if
p
::::
6
and
if,
for
each node u
of
T,
some
connected component
of
T \ u has at least three
nodes.
I
The
next
case to consider would be
when
the
tree T is defined
on
p - 2 nodes.
It
is
natural
to conjecture the existence
of
a valid inequality for
CUT~P+l
which,
by
analogy
with
(30.1.8)
and
(30.1.11), would involve, besides the
suspended
tree, a
graph
K7
with
suitable edge weights.
We
refer
to
De Souza
[1993]
for a
discussion
on
this; some examples
of
such inequalities are proposed there.
30.2
Path-Block-Cycle
Inequalities
Given
an
integer p
::::
1,
let C denote
the
circuit (1,2,
...
,p
+ 2).
Then,
the
inequality:
(30.2.1)
L
Xij
- L
Xij:::;
p(p + 1) - 2
1::;i<i::;2p+l
ijEE(C)
defines a facet of
CUT~P+l.
Indeed,
the
inequality (30.2.1) coincides
with
a
switching
of
the
(pure) clique-web inequality
(CW~P+l)T
x
:::;
0,
namely,
with
its
switching by
the
cut
8(
{I,
2,
...
,p
+ 2}) (expressed
in
(29.1.5)).
In
this
section,
we
describe a class
of
inequalities which generalizes (30.2.1).
Instead
of using
only one circuit,
we
consider a
graph
structure,
called path-block-cycle, which is
constructed
from several circuits.

30.2 Path-Block-Cycle Inequalities
493
More precisely, a path-block-cycle is a
graph
defined as follows. Let
Ch
(Vh,
E(Ch))
(1
:::;
h
r)
be
r circuits such
that
Vh
n
Vhf
=
nl<h<r
V
h
for all
distinct
h,
hi E
{I,
...
, r}.
We
suppose, moreover,
that
the
commo~
nodes are
visited
in
the
same
order along each
of
the circuits C
h
.
Then,
the
graph
with
node
set
Ul
<h<r
Vh
and
with
edge set
Ul
<h<r
E(
Ch) (allowing
repetition
of
the
edges) is called a path-block-cycle
and
is
-abbreviated
as
PBC.
It
may
contain
multiple
edges,
if
some edge is used by several
of
the
circuits C
h
.
Figure 30.2.2
shows
an
example
of
a
PBC
graph
composed
of
three circuits.
The
black nodes
are those
common
to
all three circuits;
the
three circuits are drawn, respectively,
by
a
plain
line, a thick line
and
a
dotted
line.
Figure 30.2.2: A path-block-cycle
graph
Set
nl<h<r
V
h
=:
{Xl,'"
,Xt},
where t
2':
1.
Hence, each circuit
Ch
decom-
poses into
t sUbpaths
Fih
(1
:::;
i
:::;
t), where
Fih
starts
at
Xi
and
ends
at
Xi+l
(the
indices i are
taken
modulo t). Set
Le.,
qih
is
the
number
of
internal
nodes
of
P;h,
qih
2':
o.
Let
1rb'"
,1rr-1
denote
the
r 1 largest values
taken
by
qih,
for 1
SiS
t, 1
:::;
h r. For each integer
k such
that
k(k
+ 1)
:::;
2(r
- 1), set
Finally, set
1rh·
no
:=
2p
+ 1
-I
U Vhl·
l:Sh:Sr
Given a
PBC
graph
composed
of
r circuits CJ,
...
, C
r
and which is a
subgraph
of
K2p+l,
we
define the following inequality:
(30.2.3)
Xij
- L L
Xij
S pep +
1)
- 2r.
:Si<:j:S
2p-j-l 1 <;h:Sr
;jEE(
Ch)
It
is called a path-block-cycle inequality. These inequalities
are
introduced
in
their
full generality
in
De Souza
[1993J;
a more restricted subclass (see below) is

494
Chapter
30.
Other
Valid Inequalities
and
Facets
considered
in
De Souza
and
Laurent [1995]. Actually,
they
have been
introduced
in
the
context
of
the
equicut polytope
EQCUT~p+l'
We
give first
the
characterization
of
the
PBC
inequalities
that
are valid for
the
cut
polytope, established by
De
Souza [1993].
Proposition
30.2.4.
Given a
PBC
graph that
is
a subgraph
of
K2p+l)
the in-
equality
(30.2.3) is valid for
CUT~P+l
if
and only
if
Qk
+
no
:::;
p 1 - k for all
k
E
Z+
such that
k(k
+ 1)
:::;
2(r
1).
Proof.
Denote
the
inequality (30.2.3) by v
T
x:::;
p(p + 1) - 2r.
Necessity.
Suppose
that
k is
an
integer such
that
Qk
+
no
~
p - k
and
k(k
+
1)
:::;
2(r - 1).
Then,
we
can
construct
a node set S
of
cardinality p - k whose nodes
are,
either
internal nodes
of
the
paths
P;.h corresponding
to
the
r - 1 _
k(ki1)
largest
7th
values,
or
do
not
belong
to
the
PBC
graph. Moreover,
this
set
Scan
be
chosen
in
such a way
that
v
T
6(S)
~p(p+l)-k(k+l)-2(r
1
i.e., v
T
6(S)
~p(p+l)-2r+2.
Hence,
the
cut
vector 6(S) violates
the
inequality (30.2.3).
Sufficiency. Suppose
that
Qk +
no
:::;
p - k - 1 for all k E
Z+
such
that
k(k +
1)
:::;
2(r - 1). Suppose also
that
there exists a
cut
vector 6(S) violating
(30.2.3). Set
lSI
:=
p - k for some 1
:::;
k
:::;
p 1.
Then,
v
T
6(S) =
pep
+
1)
k(k + 1)
:E
IbK2p+!
(S) n
E(Ch)1
>
pep
+ 1) - 2r.
l:Sh:Sr
Hence,
the
cut
{jK2P+1
(S)
cannot
meet all
the
r circuits
Ch.
Therefore,
the
set
nl<h<r
Vh
of
common
nodes is entirely contained
in
S
or
in
its complement.
ThIs
implies
that
(S)
can
only intersect r - A
paths
Fih
for some integer
A,
1
:::;
A:::;
r.
Then,
IbK2v+!(S)
nE(Ch)1 = 2(r - A), i.e., vT{j(S)
p(p+l)
2r+2A
k(k+l).
Thisimpliesthat2A>k(k+l),i.e.,A~
k(kt
l
+1.
Set a
IS
Vhl
and
f3
:=
ISI-
a.
These
f3
nodes
are
distributed
among
r
A:::;
r 1
paths
P;.h, which implies
that
f3
:::;
Qk.
On
the
other
hand,
a:::;
no. p k a+f3:::;
no+Qk
:::;
p-k-l,
yielding a contradiction.
This
shows
that
(30.2.3) is valid for
CUT~p+l'
I
Recall
that
the
equicut polytope
EQCUT~p+l
is
the
facet
ofCUT~p+l
defined
by
the
inequality:
:E
Xij
:::;
pep
+ 1).
l:Si<j:S2P+l
Therefore, for any facet defining inequality for
EQCUT~p+
1,
there
exists a suit-
able linear
combination
of
it
with
the
equation Ll:Si<j:S2p+l
Xij
pep
+
1)
which
produces a facet defining inequality for
CUT~PH'
In
fact,
the
inequality (30.2.3)
arises
in
this
way from
the
inequality:
(30.2.5)
:E :E
Xij
~
2r.
l:Sh5,rijEE(C
h
)
30.2 Path-Block-Cycle Inequalities
495
De Souza
[1993]
shows
that
(30.2.5) is valid for
EQCUT~p+I
if
and
only
if
no
+
Qo
:::;
p-l;
moreover, he shows
that
(30.2.3) defines a facet
of
CUT~P+I
whenever
it
is valid for
CUT~P+I
and
whenever (30.2.5) defines a facet
ofEQCUT~p+1'
A
class
of
PBC
graphs is given in De Souza
and
Laurent
[1995]
for which (30.2.5)
is facet defining for
EQCUT~p+I;
we
describe
it
below
in
Theorem 30.2.7.
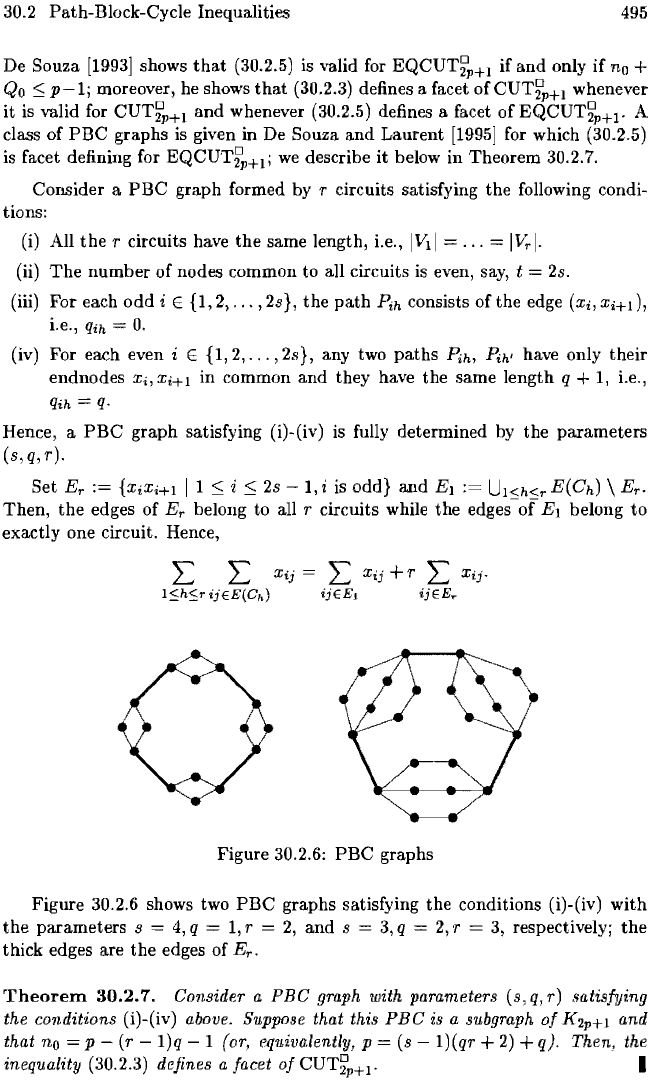
Consider a
PBC
graph formed by r circuits satisfying the following condi-
tions:
(i) All
the
r circuits have the same length, Le.,
IVII
=
...
=
1v,.1.
(ii)
The
number
of
nodes common to all circuits is even, say, t =
2s.
(iii) For each
odd
i E
{I,
2,
...
, 2s}, the
path
P,h consists of the edge
(Xi,
xi+d,
i.e., q,h =
O.
(iv) For each even i E
{I,
2,
...
,2s}, any two
paths
Pih, /{h' have only their
endnodes
Xi,
Xi+
I
in
common
and
they have the same length q +
1,
Le.,
qih = q.
Hence, a
PBC
graph satisfying (i)-(iv) is fully determined
by
the
parameters
(s,q,r).
Set
Er
:=
{XiXi+I
11
:::;
i
:::;
2s
1, i is odd}
and
El
UI<h<r
E(Ch)
\ E
r
.
Then,
the
edges of
Er
belong to all r circuits while
the
edges-of
EI
belong
to
exactly one circuit. Hence,
Xij·
Figure 30.2.6:
PBC
graphs
Figure 30.2.6 shows two
PBC
graphs satisfying
the
conditions (i)-(iv)
with
the
parameters s
4,
q =
1,
r =
2,
and
s =
3,
q =
2,
r =
3,
respectively;
the
thick edges are the edges of E
r
.
Theorem
30.2.7.
Consider a
PBC
graph with parameters
(s,q,r)
satisfying
the conditions
(i)-(iv) above. Suppose that this
PBC
is a 8ubgraph
of
K2p+I
and
that no
= p - (r
l)q
1 (or, equivalently, p = (s - 1)(qr +
2)
+ q). Then, the
inequality
(30.2.3) defines a facet
of
CUT~P+I'
I

496
Chapter
30.
Other
Valid Inequalities
and
Facets
Remark
30.2.8.
(i) De Souza
[1993]
proposes some inequalities
that
are ob-
tained
as a
common
generalization of
suspended-tree
inequalities
and
path-block-
cycle inequalities. Observe
that
the
graph
structure
used
in
suspended-treee
in-
equalities is a
suspended
tree while
the
graph
structure
used in path-block-cycle
inequalities is a collection of circuits. Note also
that
a circuit is a special case of
suspended
tree. Hence, a
natural
idea
would
be
to
consider inequalities involv-
ing a collection of suspended-trees. We refer
to
De Souza
[1993]
where several
inequalities
of
this
type
are investigated in
the
context
of
the
equicut
polytope.
(ii)
The
separation
problem
for
suspended-tree
inequalities
and
for
path-block-
cycle inequalities is
probably
hard.
Some
separation
routines
for path-block-cycle
inequalities (or, more precisely, for
the
inequalities (30.2.5) which occur for
the
equicut
polytope)
are
proposed
by
De Souza [1993]. I
30.3
Circulant
Inequalities
In
this
section,
we
present
a class of facets, whose
support
graphs
are
circulant
graphs.
The
circulant graph C (n,
r)
is
the
graph
on
the
n nodes
{I,
2,
...
,
n}
whose edges consist of
the
pairs
(i, i + 1), (i, i +
r)
for i = 1,
...
,
n,
where
the
indices
are
taken
modulo
n.
Figure 30.3.1 shows
the
graph
C(8, 3).
Figure
30.3.1:
C(8,3)
Poljak
and
Turzik
[1987, 1992] have
computed
the
maximum
cardinality
of
a
cut
in
any
circulant
graph
C (n,
r)
and
presented
new classes of facets for
the
cut
polytope
and
the
bipartite
subgraph
polytope
which are
supported
by
some
circulant
graphs.
Theorems
30.3.2
and
30.3.3
can
be
found
in
Poljak
and
Turzik
[1992]
and
Theorem
30.3.4 in
Poljak
and
Turzik
[1987, 1992].
The
bipartite subgraph polytope
BIP~
is
the
polytope
in
JRE
n
defined as
the
convex hull
of
the
incidence vectors of
the
edge sets F
~
En
for which (Vn'
F)
is
a
bipartite
subgraph
of
the
complete
graph
Kn.
Theorem
30.3.2.
Let
n,
r
be
integers with n 2 2r + 1 2
4.
Then, the
maximum
cardinality
of
a bipartite subgraph
in
C(n,r)
is equal to
max(2n
-
Ut
-
Vt
I t =
0, 1,
...
,r),
where
Ut
:=
Int - Vtr I and
Vt
is the unique integer having the
same
parity
as
n and satisfying
nt
- r
s:
Vtr <
nt
+
r.
I
Theorem
30.3.3.
Let
n =
kr
+ s where 0 < s < r <
I'
rand
k are even, s
is odd and g.c.d.(n, r) = 1. Denote by
Eo
(resp. E
1
)
the
set
of
edges (i, i +
1)

30.4
The
Parachute
Inequality
497
(resp. (i, i +
r))
for
i = 1,
...
, n
of
C(n,
r)
(the indices being taken modulo
n).
Then, the inequality:
L
Xij
+ 8 L
Xij::::
(8
+
l)n
- 8k - r
ijEE[
ijEEo
defines a facet
of
the bipartite subgraph polytope
BIP~.
I
Theorem
30.3.4.
Let
n =
kr
+ 1, where k, r
2:
2 are even integers. Then, the
inequality:
L
Xij::::
2n
- k - r
ijEC(n,r)
defines a facet
of
the
cut
polytope
CUT~.
I
Observe
that,
in
the
case r = 2,
the
circulant
C(n,2)
coincides
with
the
antiweb
AW;.
Poljak
and
Turzik
[1992]
observed
that
the
problem: "Does a
graph
G
contain
a
circulant
C(n,2)
for some n ?" is NP-complete. Hence,
the
separation
problem
for
the
class
of
inequalities:
3
L
Xij::::
"2(n
- 1), n
odd
ijEC(n,2)
is
NP-hard.
30.4
The
Parachute
Inequality
We describe
in
this
section
the
class of
parachute
inequalities.
They
have
been
introduced
l
in
Deza
and
Laurent
[1992a]
and
further
studied
in
Deza
and
Laurent
[1992c, 1992d].
The
parachute
inequality is defined
on
an
odd
number
of points, say,
on
2k
+ 1 points.
It
is convenient
to
denote
the
elements
of
the
set V
2k
+
1
as
{O,
1,
2,
...
, k, 1', 2',
...
, k'}. We define
the
following
paths
P
and
Q:
P
:=
(k,
k-l,
.
..
,2,1,
1',2',
...
,
(k-l)',
k'),
Q
:=
(k-l,
...
,2,1,
1',2',
...
,
(k-l)').
Then,
the
inequality:
(30.4.1)
(
Par
2k+l)T
x:=
L
Xij
- L (XOi
+XOi'
+Xki'
+Xk'i)
-Xkk'
::::
0
ijEP
l:'Oi:'Ok-l
is called
the
parachute inequality
and
is
denoted
as
(Par2k+lf
x
::::
o.
Fig-
ure
30.4.3 shows
the
support
graph
of
the
parachute
inequality on 7 points.
For
k even,
the
parachute
inequality is
not
valid for
the
cut
cone; for example,
it
is
violated
by
the
cut
vector 8(
{I,
3,
...
,k
- I} U {2', 4',
...
,k'}).
But,
for k
odd,
the
parachute
inequality is facet inducing.
'The
parachute
inequality
on
seven
points
(in
fact,
a
switching
of
it)
has
been
introduced
earlier
by
Assouad
and
Delorme
[19821
(cf.
Assouad
[1984]).

498
Chapter
30.
Other
Valid Inequalities and Facets
Theorem
30.4.2.
For k
odd,
k
~
3, the parachute inequality
(3004.1)
defines a
Jacet
oj
CUT
2k+l' I
Figure 30.4.3:
(Par7l
x
~
0
Figure
30.404:
The
analogue
of
(Par7
)T
x
~
0 for
CO~
30.4.1
Roots
and
Fibonacci
Numbers
As
we
now see,
the
parachute inequality presents two interesting features. First,
its number
of
roots can be expressed in terms
of
the
Fibonacci numbers; second,
there is a close connection between the parachute inequality (Par2k+l)T x
~
0
and
the
following clique-web inequality:
(CW~k':I
(1,
...
,1,
-1,
-l)l
x
:::;
O.
Recall
that
the
Fibonacci sequence is
the
sequence
(fik:::.1
defined recursively by
II
= h = 1,
Ji+2
=
Ii
+
Ji+I
for i
~
1.
We
introduce some definitions
that
we
need for
the
description
of
the roots of
the
parachute inequality. Given a subset S of
V2k+I
=
{O,
1,
...
, k, 1',
...
,
k'},
the
set S
is
called symmetric
if,
for all i E
{I,
...
,k},
i E S
if
and
only if
if
E S. Let
A = (1,2,
...
,n)
be a
path.
A subset S
of
{I,
...
,
n}
is called alternated along
the
path
A
if
IS
n {i, i +
1}1
~
1 for all i = 1,2,
...
,n
-1,
and S
is
called pseudo-
alternated
along the
path
A
if
IS
n
{i,
i +
1}1
= 1 for all i E
{I,
...
, n - I} - {j}
and
ISn
{j,j
+
I}I
0,2
for
somej
E {I,
...
,n-I}.
One can easily check
that,
for n even, there are exactly n 1 pseudo-alternated subsets S along the
path
A
for which
1,
n E S. Also,
an
easy induction shows
that
the number of alternated
subsets along
the
path
.4 = (1,
...
,n)
is equal to the Fibonacci number In+2.
Proposition
30.4.5.
IJ k is odd, then the parachute inequality (30.4.1) is valid
Jor
CUT
2
k+I' For any
k,
the roots
oj
the parachute inequality
are
the cut vectors
8(S)
Jor which S is a subset
oj
{I,
2,
...
,k,
1',2',
...
,
k'}
oj
one
oj
the Jollowing
Jour types:
Type
1:
k,
k'
E
Sand
S is pseudo-alternated along the path
P.
Type
2: k,
k'
¢.
Sand
S
i.g
alternated along the path
Q.
Type
3: For k
odd,
k E S, k'
¢.
S and (a) or (b) holds:
