Deza M.M., Laurent M. Geometry of Cuts and Metrics

530

Chapter

31. Geometric

Properties

Lemma

31.4.7.

NEG

3

=

{d

E

~~

I

Vd

E MET3}.

Proof. Let d be a distance

on

V3

and

set

d12

:=

a,

d13

:=

b,

d

2

3

:=

c.

Let us

consider

the

image

of

d

under

the

covariance

mapping

(pointed

at

position

3)

and

the

corresponding

symmetric

matrix

(

b

btc

c2

-a)

.

P:=

bt~-a

We use

the

fact

that

dE

NEG

3

if

and

only if P

~

° (recall Figure 6.2.3). Now,

P

~

° if

and

only if det P

2:

0, i.e., if 4bc -

(b

+ c - a)2

2:

0.

The

latter

condition

can

be

rewritten

as: a

2

-

2a(b +

c)

+

(b

-

c)2

~

0, which is equivalent

to

b + c -

2VbC

=

(Vb

- .jC)2

~

a

~

b + c +

2VbC

=

(Vb

+ .jC)2. Hence,

we

find

the

condition

that

Vd

E MET3. I

More generally, Bakonyi

and

Johnson

[1995]

observe

that

the

condition (31.4.6)

suffices for

the

description

of

NEG (G)

if

G is a circuit.

In

fact,

the

following

result

holds, which

is

an

analogue of

Theorem

31.3.7 (Laurent [1997c]).

Theorem

31.4.8.

The following assertions are equivalent

for

a graph

G:

(i) NEG (G) = {d E

~~

I

Vd

E

CUT(G)}.

(ii) NEG (G) = {d E

~~

I

Vd

E

MET(G)}.

(iii) G has

no

K

4

-minor.

The

identifies

the

graphs

for which

the

clique

and

metric

con-

ditions (resp. clique

and

cut

conditions) suffice for

the

description

of

the

cone

NEG(G).

The

equivalence

of

(i)

and

(iii) is

due

to Johnson, Jones

and

Kroschel

[1995]

and

that

of

(ii)

and

(iii)

to

Laurent

[1997c].

Theorem

31.4.9.

The

following assertions are equivalent

for

a graph

G:

(i)

NEG

(G)

=

{d

E

~

I

Vd

E

MET(G)

and

dK E

NEG(K)

VK

clique

in

G}.

(ii) NEG

(G)

=

{d

E

~~

I

Vd

E

CUT(G)

and

dK E

NEG(K)

VK

clique

in

G}.

(iii)

No

induced subgraph

of

G is a wheel Wn (n

2:

5) or a splitting

of

a wheel

Wn

(n

2:

4).

We conclude

this

section

with

a result

of

geometric flavor given

in

Bakonyi

and

Johnson

[1995]; it follows as a direct application of

Theorem

31.4.4.

Proposition

31.4.10.

Let

G = (Vn'

E)

be

a chordal graph, let K

1

, •

..

,Ks

denote

its

maximal

cliques

and

let d E

~E,

R >

0.

Suppose

that

there

exist

vectors

Ul,

...

,Un

E

~n

satisfying

(i)

and

(ii):

(i)

II

Ui

-

Uj

112=

d

ij

for all

ij

E

E,

31.4

The

Euclidean Distance Matrix Completion Problem

531

Oi)

for every r = 1,

...

, s, the vectors

Ui

(i E

Kr)

lie on a sphere

of

radius R.

Then there exist vectors

VI,·

••

,

Vn

sphere

of

radius R.

lJin

satisfying (i) and all

of

them lying on a

I

31.4.2

Links

Between

the

Two

Completion

Problems

There

is

an

obvious analogy between the above results

for

the Euclidean dis-

tance

matrix

completion problem and the results from Section 31.3 for the pos-

itive semidefinite completion problem. Compare, in particular, Theorems 31.3.4

and

31.4.4, as well as Theorems 31.3.7

and

31.4.8,

and

Theorems 31.3.13

and

31.4.9. Following Laurent

[1997c],

we

indicate here how to derive the results for

the Euclidean distance

matrix

completion problem from those for the positive

semidefinite completion problem.

For convenience let us introduce the following classes of graphs:

VK

(resp.

V

M

,

Vc)

denotes the class of graphs for which the clique condition (31.4.3) (resp.

metric condition (31.4.6),

cut

condition (31.4.5)) suffices

for

the

description

of

NEG(G);

and

VKM

(resp.

VKC)

denotes

the

class of graphs for which the

clique

and

metric (resp. clique

and

cut) conditions taken together suffice for the

description of NEG(G).

It

is also convenient to introduce a notation for the following classes

of

graphs,

already encountered in the previous section.

The

class 9

c

h

consists of all chordal

graphs; the class

9K4 consists

of

the graphs

that

do not contain

K4

as a minor;

and

the class 9

w

h consists of the graphs

that

do not contain a wheel Wn (n

~

5)

or a splitting of a wheel Wn (n

~

4)

as

an

induced subgraph.

Proving Theorems 31.4.4, 31.4.8

and

31.4.9 amounts to showing the equali-

ties:

VK

9ch,

VM

Vc

9K4, and

VKM

=

VKC

= 9

w

h.

For this, it suffices

to verify

the

inclusions: V

K

~

9ch,

PK

~

VK

;

Vc

~

9K4,

PM

~

VMi

and

VKc

9wh,

PKM

~

VKM·

We

do so in Lemmas 31.4.16

and

31.4.17 below.

Crucial for

the

proof

are some links between the negative type cone

and

the

elliptope. A first obvious link between

the

cone NEG(\7G)

and

the elliptope

fCG) is provided by

the

covariance mapping (as defined in (27.3.8)). Namely,

given vectors x

E

lJiE

and

d E lJiE(\i'G) satisfying:

di,n+l

= 1

for

all i E

Vn

and

dij

2

2Xij

for all

ij

E

then

(31.4.11 )

x E fCG)

dE

NEG(\7G).

Another essential tool is the following property of the Schoenberg transform from

Theorem 9.1.1: For

d E lJiE

n

,

(31.4.12)

dE

NEG(Kn)

~

exp(

-Ad)

E

f(Kn)

for all A >

O.

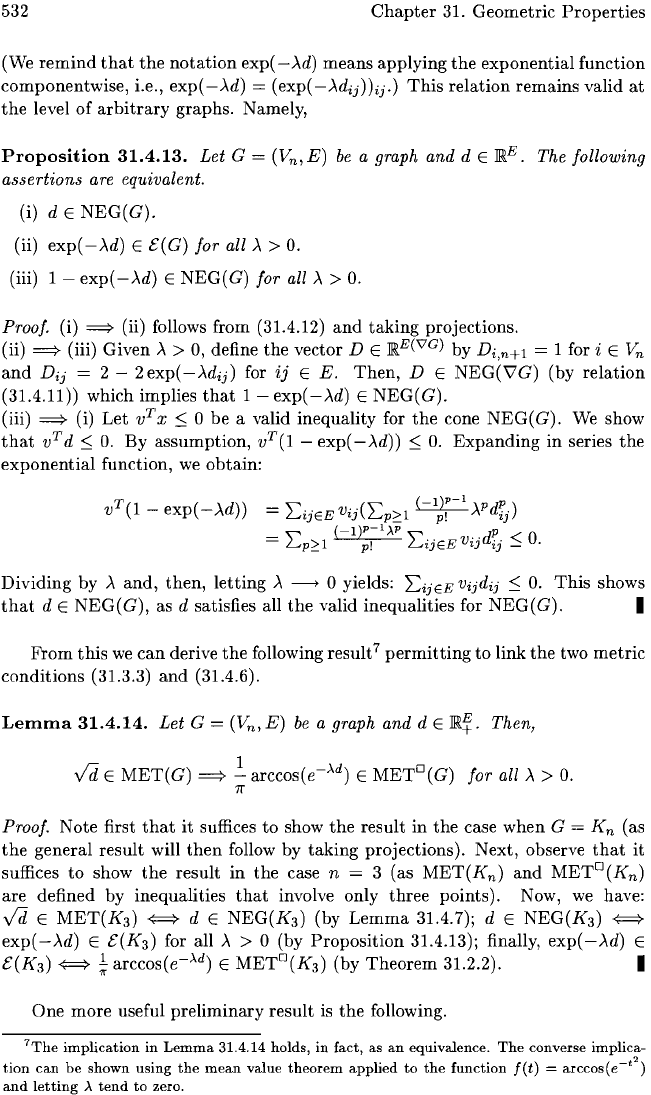
532

Chapter

31. Geometric

Properties

(We

remind

that

the

notation

exp( -

)"d)

means applying

the

exponential function

componentwise, i.e., exp(

-)..d) = (exp( -)..d

ij

) )ij.)

This

relation remains valid

at

the

level

of

arbitrary

graphs. Namely,

Proposition

31.4.13.

Let G = (Vn'

E)

be

a graph and d E

~E.

The following

assertions

are

equivalent.

(i)

dE

NEG(G).

(ii) exp( -)..d) E

e(

G) for all

)..

>

O.

(iii)

1-

exp(-)"d)

E

NEG(G)

for all)" >

O.

Proof. (i)

==}

(ii) follows from (31.4.12)

and

taking

projections.

(ii)

==}

(iii) Given).. >

0,

define

the

vector D E

~E('I7G)

by

Di,n+1

= 1 for i E

Vn

and

Dij = 2 -

2exp(-)..dij)

for

ij

E

E.

Then,

D E

NEG(\7G)

(by

relation

(31.4.11)) which implies

that

1-exp(-)"d)

ENEG(G).

(iii)

==}

(i)

Let

vTx

~

0 be a valid inequality for

the

cone

NEG(G).

We

show

that

v

T

d

~

O.

By

assumption, v

T

(1

- exp( -)..d))

~

O.

Expanding

in

series

the

exponential

function,

we

obtain:

T(1

('d))

-"

.

'("

(_l)p-l

'PdP)

V - exp

-A

-

wijEE

v'J

wp~l

p! A

ij

- "

(_l)p-l>.p"

..

dP

< 0

-

wp~l

p!

wijEE

v'J

ij

- .

Dividing by

)..

and,

then,

letting)..

----->

0 yields:

l:ijEE

Vijdij

~

O.

This

shows

that

dE

NEG(G),

as d satisfies all

the

valid inequalities for

NEG(G).

I

From

this

we

can

derive

the

following result

7

permitting

to link

the

two

metric

conditions (31.3.3)

and

(31.4.6).

Lemma

31.4.14.

Let G = (Vn,

E)

be

a graph and d E

~r

Then,

1

v'd

E

MET(G)

==}

- arccos(e->.d) E METD(G) for all

)..

>

O.

7r

Proof. Note first

that

it

suffices

to

show

the

result in

the

case

when

G =

Kn

(as

the

general result will

then

follow by taking projections). Next, observe

that

it

suffices to show

the

result

in

the

case n = 3 (as

MET(Kn)

and

METD(Kn)

are defined by inequalities

that

involve only

three

points). Now,

we

have:

v'd

E

MET(K3)

~

d E NEG(K3) (by

Lemma

31.4.7); d E NEG(K3)

~

exp( -)..d) E

e(K3)

for all

)..

> 0 (by

Proposition

31.4.13); finally, exp( -)..d) E

e(K3)

~

arccos(e->.d) E METD(K3) (by

Theorem

31.2.2). I

One

more

useful preliminary result

is

the

following.

7The

implication

in

Lemma

31.4.14 holds, in

fact,

as

an

equivalence.

The

converse

implica-

tion

can

be

shown

using

the

mean

value

theorem

applied

to

the

function

f(t)

=

arccos(e-t

2

)

and

letting>.

tend

to

zero.

31.4

The

Euclidean

Distance

Matrix

Completion

Problem

533

Lemma

31.4.15.

Let

Wn

:=

\lC

be

a wheel

on

n nodes, with

center

Uo

and

circuit

C.

Consider

the

vector

d

indexed

by

the

edge

set

of

Wn

and

defined by

d(uo,u)

:=

1

for

each node u

of

C,

d(u,v)

:=

4

for

each edge

uv

of

C.

Then,

d E

NEG(Wn)

¢=}

n is odd.

Proof.

Let x be

the

vector indexed by

the

edge set

of

C

and

taking

value

-1

on

every edge. By (31.4.11),

dE

NEG(Wn)

if

and

only

if

x E

£(C).

The

latter

holds if

and

only

if

~

arccos x E METD

(C),

that

is,

if

and

only if C has

an

even

~n~h.

I

Lemma

31.4.16.

We

have:

DK

~

9ch,

Dc

~

9K4,

and

DKC

~

9

w

h'

Proof.

We show

the

inclusion:

DK

~

9

c

h.

For this, let G =

(V,

E)

be a non-

chordal

graph

and

let C =

(V

(C),

E(

C))

be a chord less circuit

of

length

2:

4

in

G. We define a vector d E

RE

satisfying (31.4.3)

and

such

that

d

t/:

NEG(G)

by

setting

de

:=

0 for all edges e E

E(

C)

except

deo

:=

1 for one edge

eo

in

C;

de

:=

1 for every edge e joining a node of C to a node

of

V \

V(

C);

and

de

:=

0

for every edge e joining two nodes

of

V \

V(C).

The

example

from

Lemma

31.4.15 above shows

that

K4

= W

4

does

not

belong

to

Dc.

The

inclusion:

Dc

~

9K4 now follows after

noting

that

Dc

is closed

under

taking

minors.

We finally check

the

inclusion:

DKC

~

9

w

h' For this, let G =

(V,

E)

be

a

graph

in D

KC

and

let H

:=

G[UJ be

an

induced

subgraph

of

G where U

~

V.

Suppose

in a first

step

that

H is a wheel

Wn

:=

\lC

(n

2:

5)

with

center uo. Consider

the

vector d indexed by

the

edge set of G

and

defined

in

the

following

manner:

d takes value 4

on

every edge of

the

circuit C excepet value 0

on

one edge

if

n is odd; d takes value 1

on

every edge joining

the

center

Uo

of

the

wheel

to

a

node

of

C;

d takes value 1

on

an

edge between a node

of

C

and

a node outside

the

wheel; d takes value 0

on

every remaining edge (i.e.,

an

edge joining

Uo

to

a

node

outside

the

wheel or

an

edge joining two nodes outside

the

wheel).

Then

d satisfies (31.4.3)

and

d

t/:

NEG(G)

(by

Lemma

31.4.15). Moreover d satisfies

(31.4.5), i.e.,

v'd

E

CUT(G).

Indeed, say C is

the

circuit

(UI,""

Un-I)'

Then,

v'd

= 2:i,:loc( Ui) if n is even

and

v'd

=

oc(

{Ul'

un-d)

+

2:i~22

oc(

Ui) if n is

odd

and

(UI'

Un-I)

is

the

edge

of

C

on

which d takes value

O.

Finally,

if

H is a

splitting

of

a wheel

Wn

(n

2:

4),

extend

the

above vector d by assigning value 0

to every new edge

created

during

the

splitting process. I

Proof. We first verify

the

inclusion:

PK

~

D K. Let G be a

graph

in

PK;

we

show

that

G E

DK.

For this, let d E

RE

satisfying (31.4.3);

we

show

that

dE

NEG(G).

By

Proposition

31.4.13, exp(

-.\dK)

E

£(K)

for every clique K

in

G

and

every

.\

>

O.

As G E

PK,

this

implies

that

exp(-.\d)

E

£(G)

for all .\ >

O.

Using

again

Proposition

31.4.13,

we

obtain

that

dE

NEG(G).

Suppose now

that

G E

PM;

we

show

that

G E D

M

.

Let d E RE satisfy-

534

Chapter

31.

Geometric Properties

ing (31.4.6), i.e.,

.,fd

E MET(G). Then, by Lemma 31.4.14,

~

arccos(e-.xd) E

METD( G) for all A >

O.

As G E

PM,

this implies

that

exp( -

Ad)

E

e(

G) for all

A>

O.

By Proposition 31.4.13,

we

obtain

that

d E NEG(G).

The

inclusion

PKM

~

DKM

follows by combining the above arguments. I

31.5

Geometry

of

the

Elliptope

In

Section 28.4.1 was introduced the convex body

In

as a (nonpolyhedral) re-

laxation

of

the

cut

polytope

CUT~.

We

remind

that

where

.J

is the all-ones

matrix

and, for x E

JRE

n

,

X is the symmetric n x n

matrix

with

zero diagonal

and

off-diagonal entries

Xij.

We

also remind

that

the elliptope

en

is defined as the set of n x n symmetric positive semidefinite matrices with

an

all-ones diagonal. Therefore,

x E

In

<¢=?

.J

-

2X

E

en.

Hence, the two convex sets In and

en

are essentially identical (up

to

the

trans-

formation

x

1-+

1 -

2x).

The

convex body In is a relaxation of

CUT~,

i.e.,

Moreover,

In provides a good approximation for

CUT~

in the sense of opti-

mization (recall Theorem 28.4.7).

In

fact, the convex body In presents several

geometric features, which may explain and provide further insight

for

its good

behaviour in optimization. One such property is,

for

instance, the fact

that

the

only vertices

of

In

are the cut vectors. This result is given below as well as sev-

eral other geometric properties. For convenience

we

will work with the elliptope

en

rather

than

with

In

itself.

We

start

with

recalling some definitions. Let K be a convex set in

JRd.

Given

a

boundary

point

Xo

of

K,

its normal cone

N(K,

xo)

is

defined as

N(K,xo}

:=

{c

E

JRd

I

S;

c

T

Xo

for

all x E

K}.

Hence,

N(K,xo)

consists

of

the normal vectors to the supporting hyperplanes of

Kat

Xo.

Then,

the supporting cone

at

Xo

is defined

by

C(K,xo)

:=

{x

E

JRd

I

S;

0 for all c E

N(K,xo)}.

The

dimension of the normal cone

permits

to classify the boundary points.

In

particular, a boundary point

Xo

is called a vertex

of

K

ifits

normal cone

N(K,

xo)

is full-dimensionaL A subset F

~

K is a face

of

K

if,

for all x E F, y, z E K and

31.5 Geometry

of

the

Elliptope

535

o

::;

a

::;

1,

x =

ay

+

(1

a)z

implies

that

y, z E

F.

In

particular, an element

Xo

E K is called

an

extreme

point of K

if

the set {xo} is a face of

K.

In

what

follows

we

consider

the

two convex sets

En

and

.In. When dealing with

En

we

take

the

space of symmetric n x n matrices as ambient space, equipped with the

inner

product:

n

(A,

B)

:=

2:

aijbij for two symmetric n x n matrices B

i,j""l

and, when dealing with

.l

n

,

the ambient space is the usual Euclidean space

(

"+1)

1R

2 •

We

remind

that

'It

A

:=

l:i=l aii for an n x n

matrix

A.

We

begin with the description of the polar of

En

and

of its normal cones.

These results are established by Laurent

and

Poljak [1995b, 1996aJ; proofs can

be found there.

Theorem

31.5.1.

The polar

of

En

is given by

(Ent

=

{D

- M I M

~

O,D diagonal

matrix

with

'It

D = I}.

For A E En, its

normal

cone is defined by

N(En,A)

=

{D

- M I M

~

0,

(M,A)

= O,D diagonal

matrix}.

Moreover, dim

N(En,

A)

n + (n-;+l), where

l'

is the rank

of

A.

I

Corollary

31.5.2.

The

only

vertices

of

En

are the

'cut

matrices'

xxT,

for

x E

In

other

words, the convex body

.I

n

has 2

n

-

1

vertices,

namely,

the

cut

vectors ti(8)

for

8

I:;::

V

n

.

I

We

remind

that,

given c E

REn,

max( c

T

x I x E .In) is

an

upper

bound

for the max-cut problem: max(c

T

x I x E

CUT~).

Equality holds between

the

bound

and

the

max-cut precisely when c belongs

to

the

normal cone

of

one of

the

cut

vectors.

That

the

cut

vectors are

the

only boundary points having a full

dimensional normal cone supports the idea

that

.I

n

approximates well

CUT~.

From Theorem 31.5.1 one obtains

that

the supporting cone C(En'

A)

at

A E

En

is the set

{Xsymmetricnxnlxii

OVi 1,

...

,n,

b

T

Xb"2::.0 for all

bE

KerA}.

In

particular,

at

A J (the all-ones matrix), the supporting cone is

-NEG

n

.

At every

other

vertex

of

En,

the

supporting cone is an affine image of the nega-

tive

type

cone

NEG

n

(under

the

switching mapping). So, this makes one more

connection between the elliptope

and

the negative type cone.

We

now

turn

to

the

description of the faces of En.

We

remind

that

En

is

obtained by taking the intersection of the cone PSD

n

of positive semidefinite

matrices with

the

linear space W

{X

I Xii 1

Vi

1,

...

,n}.

The

facial

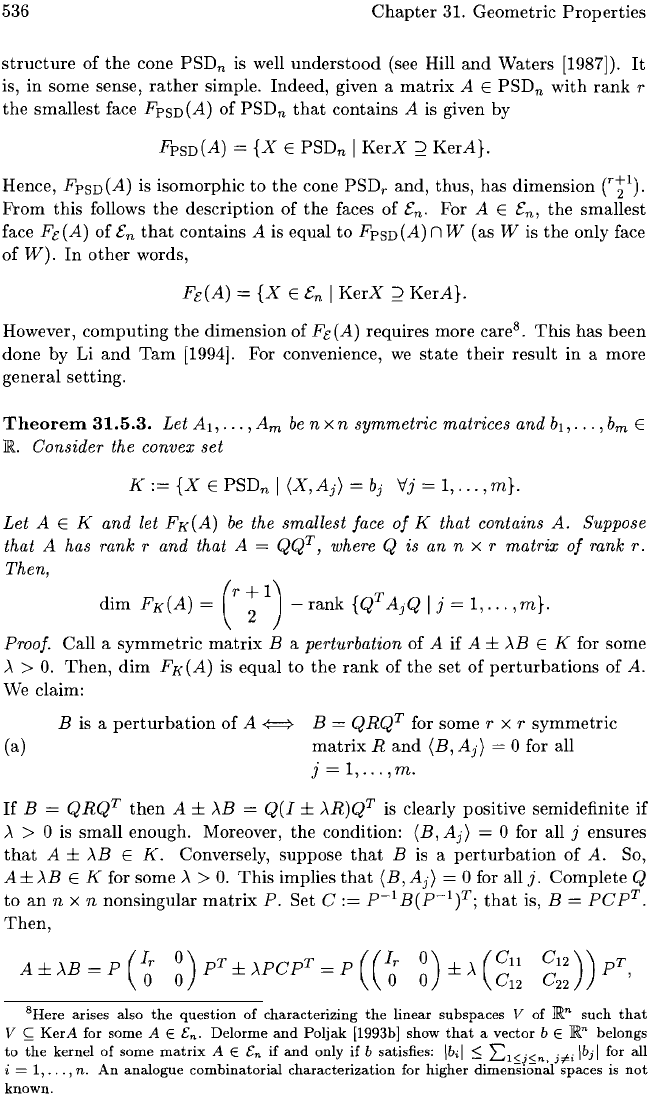
536

Chapter

31. Geometric

Properties

structure

of

the

cone

PSD

n

is well

understood

(see Hill

and

Waters

[1987]).

It

is, in some sense,

rather

simple. Indeed, given a

matrix

A E

PSD

n

with

rank

r

the

smallest

face FpSD(A) of

PSD

n

that

contains A is given by

FpSD(A) =

{X

E

PSD

n

I

KerX

2 KerA}.

Hence,

FpSD(A) is isomorphic

to

the

cone

PSD

r

and,

thus, has

dimension

C!l).

From

this follows

the

description

of

the

faces of

En.

For A E

En,

the

smallest

face

Fe

(A) of

En

that

contains A is equal

to

F

pSD

(A) n W (as W is

the

only face

of

W).

In

other

words,

FdA)

=

{X

E

En

I

KerX

2 KerA}.

However,

computing

the

dimension

of

FdA)

requires more care

8

.

This

has

been

done

by

Li

and

Tam

[1994]. For convenience,

we

state

their

result

in a

more

general

setting.

Theorem

31.5.3.

Let

AI,

.

..

,Am

be

n x n

symmetric

matrices and b

1

, .

..

,b

m

E

R Consider the convex set

K:=

{X

E

PSD

n

I

(X,Aj)

= b

j

Vj = 1,

...

,m}.

Let

A E K and let

FK

(A)

be

the smallest face

of

K that contains

A.

Suppose

that A has rank r and that A

=

QQT,

where Q is an n x r

matrix

of

rank

r.

Then,

dim

FK(A)

=

(r;

1)

_

rank

{QT

AjQ

I j =

1,

...

,m}.

Proof.

Call

a

symmetric

matrix

B a perturbation of A if A ±

)"B

E K for some

)..

>

O.

Then,

dim

FK

(A) is equal

to

the

rank

of

the

set

of

perturbations

of A.

We claim:

B is a

perturbation

of

A

~

B =

QRQT

for some r x r

symmetric

(a)

matrix

Rand

(B,

Aj)

= 0 for all

j =

1,

...

,m.

If

B =

QRQT

then

A ±

)"B

=

Q(I

± )..R)QT is clearly positive semidefinite

if

)..

> 0 is

small

enough. Moreover, the condition: (B,

Aj)

= 0 for all j ensures

that

A ± )"B E

K.

Conversely, suppose

that

B is a

perturbation

of

A.

So,

A±)"B

E K for some).. >

O.

This

implies

that

(B,

A

J

)

= 0 for all

j.

Complete

Q

to

an

n x n nonsingular

matrix

P.

Set

C:=

P-

1

B(P-

1

f;

that

is, B =

PCpT.

Then,

0)

±)..

(C

ll

o C

12

8Here

arises also

the

question

of

characterizing

the

linear

subspaces

V

of

llt

n

such

that

V

<;;

KerA

for

some

A E En.

Delorme

and

Poljak

[1993b]

show

that

a

vector

b E llt

n

belongs

to

the

kernel

of

some

matrix

A E

En

if

and

only if b satisfies:

Ib;j

::;

Ll<j<n,

j'l'i

Ib

j I for all

i = 1,

...

,n.

An

analogue

combinatorial

characterization

for

higher

dimensional

spaces

is

not

known.

31.5

Geometry

of

the

Elliptope

537

. C

(Cll

Cu)

H

(Ir

0)

,(Cn

C12)

>--

0

Th···

l'

settmg

:=

C12

C22

. ence, 0 0 A

C12

Cn

-'

IS

Imp les

that

C12

=

C22

=

O.

Therefore, B

QCnQT,

where ClI is a symmetric

r'

x r

matrix.

Hence, (a) holds.

~ow,

every

perturbation

of A is of

the

form B QRQT

with

(B,

Aj)

= 0 for

all

j;

that

is, (R, Q1'AiQ) 0 for all

j.

Hence,

the

dimension

of

FK(A)

is equal

to

the

dimension of

the

orthogonal complement of {Q1'

AjQ

I j = 1,

...

,m}

in

the

space of symmetric r x r matrices. Hence,

we

have

the

desired formula for

dim

FK(A).

I

Corollary

31.5.4.

Let A E

t:n

with rank

r,

let Fe(A) denote the smallest

face

of

t:n

containing

A,

and suppose that A is the Gram

matrix

of

the vectors

Ul,""U'"

ERr,

Then,

(31.5.5)

dim Fe(A)

(

r+

1)

2 - rank

{uiuf

I i = 1,

...

, n}.

I

In

particular, one obtains bounds for

the

rank of extreme matrices

9

of

t:n.

Corollary

31.5.6.

Let

A E

t:n

with rank

r.

If

A is

an

extreme point

of

t:n

then

(rtl)

~

n. I

Moreover, as

we

see below, for every r such

that

("tI)

~

n there exists

an

extreme

matrix

in

t:n

having rank r.

The

formula (31.5.5) can

be

used for finding

the

possible dimensions for

the

faces of

t:n,

as observed in Laurent

and

Poljak

[1996aJ. Namely,

Proposition

31.5.7.

Let

A E

t:n

with rank r and

set

k

:=

dim Fe(A). Then,

Moreover,

for

every integers r, k

2::

0 satisfying the above inequality, there exists

a

matrix

A E

t:n

with rank r

and

with

dim

Fe(A) k.

Proof.

The

inequality from Proposition 31.5.7 follows from (31.5.5), after noting

that

r

~

rank

{Ul

ui,

...

,

Un

ur}

~

n.

The

existence

part

relies essentially

on

a construction proposed

in

Grone, Pierce

and

Watkins

[1990J,

which goes as

follows. Let

el,

...

, e

r

denote

the

coordinate vectors in lIr'

and

set

Wij

Ji(

ei

+

ej)

for 1

~

i < j

~

r. Then,

the

(rtl) matrices: (i

1,

...

,r)

and

WijW~

(1

~

i < j

~

'r) are linearly independent. Suppose first

that

n

rtI)

- k where

this

question

has

been

the

subject

of several

papers

in

the

linear

algebra

literature;

for

example,

by

Christensen

and

Vesterstr>,m [1979], Loewy [1980], Grone,

Pierce

and

Watkins

[1990].

538

Chapter

31. Geometric

Properties

k

~

G).

Hence, r

~

n

~

C!l).

Define A as

the

Gram

matrix

of

the

following

n vectors:

e1,

...

, e

r

together

with

n - r

of

the

vectors

Wij.

By

construction, A

has

rank

r

and

dim

FdA)

=

C!l)

- n =

k.

When

n >

C!l)

-

k,

we

can

take

as

matrix

A

the

Gram

matrix

of

the

following n vectors:

e1

repeated

n-

C!l)

+k+

1

times,

e2

.•.

e

r

,

and

G)

- k

of

the

Wij'S.

I

Therefore,

the

range

Vn

of

the

possible values for

the

dimension

of

the

faces

of

En

is given by:

where

k

n

is

the

smallest integer k such

that

(k!2) - n >

(~n)

+ 1, i.e.,

2k

n

>

n;

that

is, k

n

= l I J +

1.

For instance,

k3

=

2,

V3

=

[0,1]

U

{3},

k4

=

3,

V

4

= [0,3] U {6},

k5

= 3, V5 = [0,3] U [5,6] U {10},

k6

=

4,

V6

= [0,6] U [9,10] U {15},

k7

=

4,

V

7

= [0,6] U [8,10] U [14,15] U {21}.

One

can

verify

on

Figure

31.3.6

that

the

proper

faces

of

E3

have dimension

°

(extreme

points) or 1

(an

edge between two

cut

vectors;

there

are six such

faces). A detailed description of

the

faces

of

En

can be found

in

Laurent

and

Poljak

[1995b, 1996a] for n = 3

and

n =

4,

respectively.

Finally,

the

possible dimensions for

the

polyhedral

faces of

En

are as follows;

they

were

computed

by

Laurent

and

Poljak [1996a].

Theorem

31.5.8.

If

F is a polyhedral face

of

En

with dimension k, then

(kr)

~

n - 1. Moreover,

if

all the vertices

of

F are

cut

matrices then F is

a simplex. Conversely, for every integer k

;::::

1 such that (k!l)

~

n -

1,

En

has

a polyhedral face

of

dimension k (which can

be

chosen

to

be

a simplex with cut

matrices as vertices).

I

Every

polyhedral

face

of

En

with

cut

matrices as vertices yields clearly a face

of

the

cut

polytope. We describe below a

construction

for such

polyhedral

faces,

due

to

Laurent

and

Poljak

[1996a]. We need a definition

in

order

to

state

the

result.

Let

Sl,

...

,

Sk

be k subsets

of

V

n

.

The

cut

vectors O(Sl),

...

,

O(Sk)

are said

to

be in general position

if

the

set

n Si n n

(Vn

\ Si)

iEI

if.!

31.6 Adjacency Properties

539

is nonempty, for every subset I

<;;;

{I,

...

,

k}.

This implies

that

2/c

:::;

n, i.e.,

k

:::;

log";!

n. Moreover, the

cut

vectors li(S1)"

..

,li(S/c) are linearly independent.

Theorem

31.5.9.

Let

li(S1),''''

li(S/c)

be

k cuts

in

general position. Then,

the

set

F Conv(8(St),

...

, li(S/c)) is a face

of

the convex

body

In- (Equiva-

lently, the

set

Conv(x1xf,

...

,

x/exf)

is a face

of

en)

where

Xh

E llt

n

is defined

by

xh(i)

1

if

i E Sh

and

xh(i)

-1

if

i E

Vn

\

Sh,

for h = 1,

...

)

k.)

Therefore,

F is also a face

of

the

cut

polytope I

This

result shows

that

In

and

CUT~

share fairly many common faces,

up

to dimension llog2nJ.

This

supports

again

the

idea

that

In

approximates well

the

cut

polytope

CUT~.

In

fact,

the

faces considered

in

Theorem 31.5.9 are also

faces in common with

the

semimetric polytope

MET~;

see Theorem 31.6.4.

31.6

Adjacency

Properties

We

now

return

to

the

study

of

the

geometry of

the

cut

polytope itself, as well

as with respect to its linear relaxation by

the

semimetric polytope. We mention

first some results on the faces of low dimension and, then, facts

and

questions

about

the

small cut

and

semimetric polytopes.

31.6.1

Low

Dimension

Faces

A striking property of the cut polytope

CUT~

is

that

any two

of

its vertices

form

an

edge

of

CUT~.

In

fact, much more is true.

In

order the formulate

the

results,

we

need some definitions.

Let

P be a polytope

with

set of vertices

V.

Given

an

integer k

2:

1,

the

polytope P

is

said to be k-neighborly

if,

for any subset W

<;;;

V of vertices such

that

IWI

:::;

k,

the

set

Conv(W)

is a a face of

P.

This implies, in particular,

that

every k vertices of

Pare

affinely independent. Hence, every polytope

is

I-neighborly

and

a polytope is 2-neighborly precisely when its I-skeleton

graph

is a complete graph.

Given

an

integer d

and

a polyhedron P,

we

let

cPd(P)

denote

the

set of

d-

dimensional faces of

P.

Barahona

and

Mahjoub

[1986]

show

that

CUT~

is 2-neighborly, i.e.,

that

any

two

cut

vectors are adjacent on

CUT~.

In

other words,

the

I-skeleton

graph

of

CUT~

is a complete graph.

Padberg

[19891

shows the following stronger result:

Any two

cut

vectors

are

adjacent on the rooted semimetric polytope

RMET~

(de-

fined by

the

triangle inequalities going through a given node; recall Section 27.2).

More generally, Deza, Laurent

and

Poljak

[1992]

show

the

following result.

Theorem

31.6.1.

Let

W

be

a

set

of

cut vectors such that

IWI

:::;

3. Then, the

set

Conv(W)

is a

simplex

face

of

the

semimetric

polytope

MET~.

Deza M.M., Laurent M. Geometry of Cuts and Metrics

Подождите немного. Документ загружается.