Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.


384
Chapter
25.
Cut
Lattices, Quasi h-Distances
and
Hilbert Bases
Proposition
25.1.5.
Let n
:::
6
be
an even integer and let d E
?lEn.
Then, d
belongs to the even cut lattice
?l(K~n)
if
and only
if
d satisfies the parity condition
(24.1.1)
and
the following conditions:
(i)
:L
dU,j)
0
(mod
4).
l::;i<j:Sn
(ii)
:L
d(i,j)
:L
d(i,k)
0
(mod
8) for all k E
Vn
-in
the case
i<j,i,jEV"
\{k}
i(V"
\{k}
when n
==
0
(mod
4).
(iii) d(h, k) +
:L
d(i,j)
:L
(d(i, h) + d(i,
k))
==
0
(mod
8)
i<j,i,j(V
n
\{h,k}
iEV"
\{h,k}
for
all h
'"
k E
Vn
in the case when n 2
(mod
4). I
It
is
not difficult to extend the result for even T-cuts. Namely,
Proposition
25.1.6.
Let
T
~
Vn
with
ITI
even, 2
:s:
ITI
:s:
n -
1.
let d E
?lEn.
Suppose first that
ITI
2,
T
:=
{s, t}. Then, d E
?l(K~)
if
and only
if
d
satiBfies the parity condition
(24.1.1) and the conditions:
drs
=
0,
dri = d
si
for
all i E
Vn
\
T.
Suppose now that
ITI
:::
4. Then, d E
?l(K~)
if
and only
if
d
satisfies
(24.1.1) and the following conditions:
(i) dij
0 (mod
4).
Oi)
Qn(1,
...
,1,
-1,
...
,-1,2,
...
,2,0,
...
,O)T d
==
0 (mod 8), where there are
, y
'~
T
Vn\T
exactly
a:
coefficients 1, and;3 coefficients 2,
for
the following values
of
a:,
;3:
(iia)
(a:
= 1,;3 = 0) and
(0:
=
2,
,8
= 1)
if
ITI
==
0
(mod
4),
(iib)
(a:
= 2,;3 =
0)
and
(0:
= 1,;3 =
1)
if
ITI
==
2
(mod
4).
I
A characterization
of
the
odd
cut
lattice
?l(K~dd)
is known only in the case
n =
6.
So, ?l(K6
dd
) is the lattice
in
IRls
generated by
the
16
cut
semimetrics
8(
{i})
(1
:s:
i
:s:
6)
and
8(
{I,
i,j})
(2
:s:
i < j 6).
We
need
the
following
notation. Given distinct
a,
b,
c E
V6,
let
va,be
E
be
the
vector defined by
{
va,be
=
va,bc
= 1 a,be - 2
ab
ac
,vbc
~
,
a,be -
2
v
ij
-
a,bc 2 a,bc a,bc 1
v
ai
= - ,
Vb;
vci -
for i
'"
j E
V6
\ {a,
b,
c},
for i E
V6
\
{a,b,c}.
Consider
the
conditions:
(25.1.7)
(va,bcf
X
:s:
0 for all distinct
a,
b,
c E
V6,
(25.1.8)
(Va,be?
x
==
0
(mod
4)
for all distinct a,
b,
c
l/6,

25.2
Quasi
h-Distances
385
(25.1.9)
(V1,bc)T
x_(v1,b1c')T X
==
0
(mod
12) for 2
:::::
b <
c:::::
6,
2:::::
b'
< c'
:::::
6.
The
next result from Deza
and
Laurent [1993a] gives
the
characterization
of
the
odd
cut
lattice
Z(.qdd), also
of
the
cone
ll4
(Kgdd)
and
of
the
integer cone
Z+(Kgdd).
Proposition
25.1.10.
(i)
Let
d E
~!6.
Then,
dE
ll4(Kgdd)
if
and
only
if
d satisfies (25.1.7).
(ii)
Let
d E Z
E
6.
Then,
d E
Z(Kgdd)
if
and
only
if
d satisfies (25.1.8)
and
(25.1.9).
(iii)
Let
dE
Z!6.
Then,
d E
Z+(Kgdd)
if
and
only
if
d satisfies (25.1.7), (25.1.8),
and
(25.1.9). I
An
immediate
consequence of
Proposition
25.1.10
is
that
the
family
of
odd
cut
semimetrics
on
V6
forms a Hilbert basis; see Section 25.3.
Further
information
on
sublattices
of
the
cut
lattice
.en
can
be
found
in
Deza
and
Grishukhin
[1996a].
25.2
Quasi
h-Distances
Let d
be
a
distance
on
V
n
.
Then,
d is called a quasi
h-distance
if
d E
CUT
n n
.en
and
d
is
not
hypercube
embeddable.
In
other
words, d
can
be
decomposed
both
as a
nonnegative
combination
of
cut
semimetrics
and
as
an
integer
combina-
tion
of
cut
semimetrics,
but
not as a
nonnegative
integer
combination
of
cut
semimetrics.
We
remind
that
the
smallest integer
TJ
such
that
TJd
is
hypercube
embeddable
is called
the
minimum
scale of d
and
is
denoted
by
1/(d).
As
stated
in
Theorem
24.1.3, there are no quasi h-distances
on
n
:::::
5 points.
We have seen already several ways of
constructing
quasi h-distances.
Quasi
h-distances
can
be constructed, for instance, using
the
antipodal
extension op-
eration
(described
in
Section 7.2). Indeed, let d
be
a distance
on
Vn
which
is
hypercube
embeddable
and
let Q E
Z+
such
that
Sfl
(d)
:::::
Q <
sh(d).
Then,
ant,,(d) is a quasi h-distance. Recall
that
ant,,(d)
is
the
distance
on
V
n
+
1
de-
fined
by
ant,,(d)(1,n +
1)
=
Q,
ant,,(d)(i,n
+
1)
= Q - d(1,i) for
1:::::
i:::::
n,
and
ant,,(d)(i,j) =
d(i,j)
for 1
:::::
i < j
:::::
n. As
an
example, for n
::::
6,
the
distance
d~
:=
2d(Kn
\e)
(taking
value 2
on
all pairs except value 4
on
the
pair
corresponding
to
the
edge
e)
is a quasi h-distance (as
d~
= ant4(2:D.n-l); see
Example
7.2.7).
The
gate
extension
operation
(described
in
Section 7.1)
permits
also
to
con-
struct
quasi h-distances.
If
d
is
a distance
on
Vn
and
Q E
ll4,
its
gate
extension
gat",(d) is
the
distance
on
Vn+l defined by gat,,(d)(1,n + 1) =
Q,
gat",(d)(i,n +
1) = Q+d(1,i) for
1:::::
i:::::
n,
and
gat",(d)(i,j)
=
d(i,j)
for
1:::::
i < j::::: n.
Then,
for Q E
Z+,
gat", (
d)
is a quasi h-distance
if
and
only
if
d is a quasi h-distance.

386
Chapter
25.
Cut
Lattices, Quasi h-Distances
and
Hilbert Bases
This
implies, in particular,
that
there
is
an
infinity
of
quasi h-distances on n
points for all n 2
7.
Indeed, all gate extensions
of
df,
=
2d(K6\e)
are quasi
h-distances.
As
the
following result by
Laburthe
[1994]
indicates,
other
examples
of
quasi
h-distances
on
6 points
can
be constructed.
It
implies, moreover,
that
there
is
also
an
infinity
of
quasi h-distances on 6 points.
Lemma
25.2.1.
Let e
be
an edge
of
K6 and let v
be
a node
of
K6 which is not
adjacent to
e. Then, the distance 2d(K6
\e)
+
m8(
{v})
is a quasi h-distance for
each integer m
2
o.
Proof. Suppose K6
is
the
complete
graph
on
V6
=
{I,
...
,6},
e
is
the
edge
(1,6)
and
v
is
the
node
2.
Set
d:=
2d(K6\e)+m8({v}).
Let d =
I:sas8(S)
be a
Z+-
realization
of
d,
with
as
E
Z+.
As d satisfies
the
triangle equality: d
16
= d
li
+di6
for i =
3,4,
5,
we
deduce
that
as
= 0 if S
is
one
of
the
sets: 3,
4,
5,
16, 23, 24,
25, 34, 35, 45, 126, 136, 146,
and
156. Hence, d =
I:sEs
as8(S),
where S
may
contain
the
sets:
1,
2,
6,
12,
13,
14, 15,
26, 36,
46,
56, 123, 124, 125, 134, 135,
145.
By
computing
d
12
, d
26
,
and
d
16
,
we
obtain, respectively,
m + 2 =
a2
+
a6
+
al2
+
a36
+
a46
+ 0!56 +
a123
+
al24
+ 0!125 ,
4 =
Las
-a2·
SES
Adding
the
first two relations
and
subtracting
the
third
one,
we
obtain
that
a2
=
m.
Therefore, if d
is
hypercube embeddable,
then
so
is
d -
m8(
{2}).
This
contradicts
the
fact
that
2d(K6\e)
is
a quasi h-distance. I
In
fact, as a consequence
of
Theorem
25.2.2 below, there are no
other
quasi
h-distances
on
6 points besides those described in
Lemma
25.2.1.
Theorem
25.2.2
and
Corollary 25.2.3 were proved by
Laburthe
[1994, 1995].
The
proof
of
The-
orem
25.2.2 involves
many
technical details, so
we
do
not
give
it
here. (Details
about
the
full
proof
can
also be found in
Laburthe,
Deza
and
Laurent
[1995].)
Theorem
25.2.2.
Every quasi h-distance on
VI>
is a nonnegative integer
sum
of
cuts and
of
the distances
2d(K6\e),
for
e
edge
of
K
6
. I
Corollary
25.2.3.
The only quasi h-distances on
VI>
are
of
those
of
the
form
2d(K6\e)
+
m8({v}),
where e is an edge
of
K6, v is a node
of
K6
not
adjacent
to
e, and m E
Z+.
The
proof
of
Corollary 25.2.3 uses
the
identities (a)-(i) below, which show
that
all
the
perturbations
of
2d(K6\e)
(obtained by adding a
cut
semimetric),
other
than
the
one considered in
Lemma
25.2.1, are hypercube embeddable. For 1
::;
i < j
::;
n,
let
eij
denote
the
edge
ij
of
K
6
•
Then,
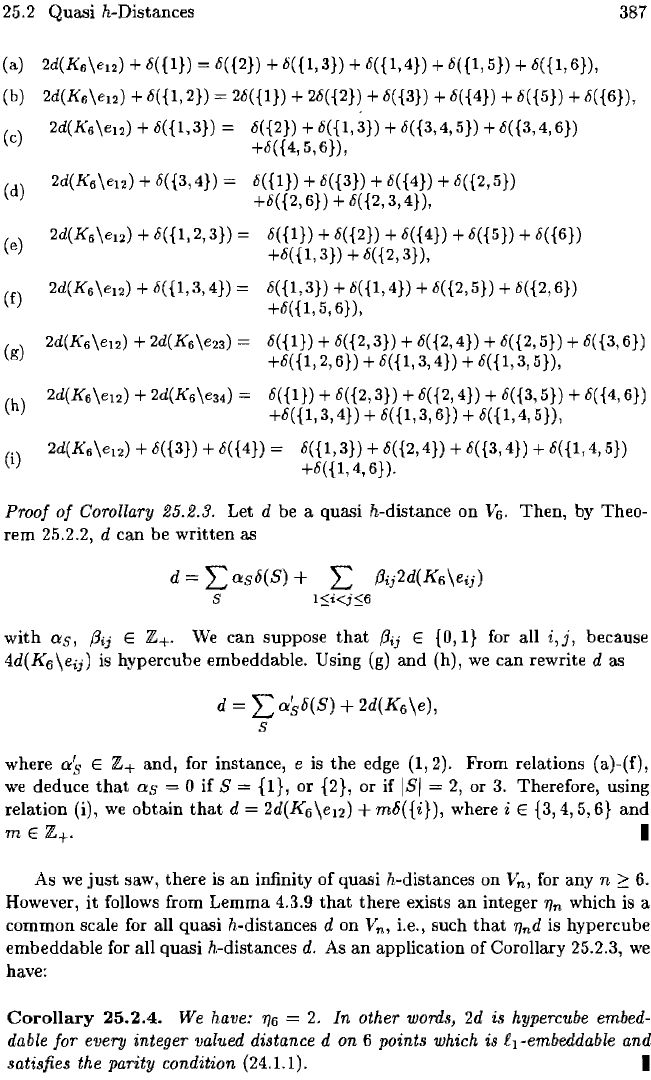
25.2 Quasi h-Distances
387
(a.)
2d(K
6
\e12) + 8({1}) 8({2})
+8({1,3}) +8({1,4})
+ 8({1,5}) + 8({I,B}),
(b)
2d(K
6
\e12)
+8({1,2})
28({1}) + 28({2}) + 8({3}) + 8({4}) + 8({5}) +8({B}),
2d(K
6
\e12) + 8(
{I,
3})
==
8(
{2}) + 8(
{I,
3}) + 8( {3, 4, 5}) + 8( {3, 4, B})
(e)
(d)
(e)
(f)
+8({4,5,B}),
2d(K
6
\e12) + 8({3,4}) = 8({1}) + 8({3}) + 8({4}) + 8({2,5})
+8(
{2,
B})
+ 8( {2,
3,4}),
2d(K
6
\e12)
+8({1,2,3})
==
8({1}) + 8({2}) + 8({4})
+8({5})
+ 8({6})
2d(K
6
\en}
+ 8({1,3,4}) =
+8({1,3})
+8({2,3}),
8({1,3}) + 8({1,4}) + 8({2,5}) + 8({2,B})
+8({1,5,B}),
8({1}) + 8({2,3}) +
8(
{2,4}) + 8({2, 5}) + 8( {3,B})
+8(
{I,
2,
B})
+ 8({1, 3,4}) + 8( {1,3, 5}),
(h)
2d(K6\e12) +
2d(K
6
\e34)
==
8({1}) + 8({2,3}) + 8({2,4}) + 8({3,5}) + 8({4,6})
+8({1,3,4})
+ 8({1,3,B}) +
8({1,4,5}),
(i)
2d(K
6
\e12) + 8({3}) + 8({4})
==
8({1,3}) + 8({2,4}) + 8({3,4}) +
8({1,4,5})
+8({1,4,6}).
Proof
of
Corollary 25.2.3. Let d be a quasi h-distance on
V6.
Then, by Theo-
rem 25.2.2,
d can be
written
as
d =
L>~s6(S)
+
2:
i3ij2d(K6\eij)
s
I$i<iS6
with
as,
i3ij
E Z+.
We
can suppose
that
i3ij
E
{O,
I} for all i,
j,
because
4d(K
6
\eij)
is hypercube embeddable. Using (g) and (h),
we
can rewrite d as
d =
2:a86(S)
+
2d(K
6
\e),
S
where
as
E and, for instance, e is
the
edge (1,2). From relations (a)-(f),
we
deduce
that
as
= 0
if
S =
{I},
or {2},
or
if
lSI
=
2,
or
3.
Therefore, using
relation (i),
we
obtain
that
d
2d(K
6
\e12)
+
m6({i}),
where i E
{3,
4,5,6} and
mE
Z+. I
As
we
just
saw, there
is
an
infinity
of
quasi h-distances on V
n
,
for any n
~
6.
However,
it
follows from Lemma 4.3.9
that
there exists
an
integer
'fin
which
is
a
common scale for all quasi h-distances
don
V
n
, i.e., such
that
'find
is
hypercube
embeddable for all quasi h-distances
d.
As
an
application
of
Corollary 25.2.3,
we
have:
Corollary
25.2.4.
We have:
'fI6
2.
In
other words,
2d
is hypercube embed-
dable for every integer valued distance d on
6 points which is iI-embeddable and
satisfies the parity condition
(24.1.1). I

388
Chapter
25.
Cut
Lattices, Quasi h-Distances
and
Hilbert Bases
For
the
cla..'ls
of
graphic distances,
the
following results have been shown
in
Chapter
21:
The
minimum
scale
of
the
path
metric
of
a connected
graph
on
n
nodes is equal
to
1, or is
an
even integer less
than
or equal
to
n -
2.
Moreover,
for
an
£l-rigid graph,
the
minimum
scale is equal to 1 or
2.
Much
of
the
treatment
of
Chapter
23
can
be
reformulated in
terms
of mini-
mum
scales. Indeed, consider
the
metric d
n
ant2(:n.n) (this is the
path
metric
of
the
graph
Kn+1
\e)). Then,
2td
n
2t
antz(:n.n) ant4t(2t:n.n)
is hypercube embeddable
if
and
only if 4t
::::
8h(2tl
n
).
Therefore,
the
minimum
scale
17(d
n
)
can
be
expressed as
In
particular, Theorem 23.3.1 (i) implies:
(i)
17(
d4t)
::::.
2t
with
equality
if
and
only if
there
exists a
Hadamard
matrix
of
order
4t.
Compare
(i)
with
the
next
statement
(ii), which follows from Theorems 22.0.6
and
22.0.7.
(ii)
17
1
(:n.
t
2+t+2)
::::.
2t
with
equality
if
and
only if there exists a projective plane
of order
t (where, for a hypercube embeddable distance
d,
17
1
(d)
denotes
the
smallest integer A (if any) such
that
Ad
is not h-rigid, i.e.,
has
at
least
two distinct Z+-realizations.)
Some quasi h-distances
can
also
be
constructed using
the
spherical extension
operation
(described
in
Section 7.3).
The
examples from Lemmas 25.2.5
and
25.2.6 below are
taken
from Deza
and
Grishukhin
[1994].
Recall
that,
if d is a
distance
on
Vn
and
t E ll4,
its
spherical t-extension is
the
distance spht
(d)
on
defined by
sp~(
d)(i, n +
1)
= t for all 1
::;
i
::;
n,
and
spht(d)(i,j)
dei,
j)
for
aliI::;
i < j
::;
n.
If
dE
CUTn
and
2t::::'
8£1 (d),
then
sp~(d)
E
CUT
n
+
1
.
As
a first example, consider
the
distance
where
n,
t are positive integers, i.e.,
O~
is
the
distance on
Vn
defined by
{
O~(n
l,n)
O~(i,
n
1)
O~(i,j)
= 2t,
O~(i,
n) = t
=2
for
1
::;
i
::;
n -
2,
for 1
::;
i < j
::;
n -
2.
Clearly,
O~
admits
the
following decompositions:
O~=
L
8({i,n})+(t-1)8({n-l})+(t-n+3)8({n}),
1:S;;:5n-2

25.2
Quasi
h-Distances
389
B~
=
~
CS~-2
(8(
{i, n - I}) +
8(
{i,
n}))
+ (2t - n +
2)
(8(
{n
- I}) +
8(
{n}))
.
This
shows
that
B~
is
hypercube
embeddable
ift
2:
n-3
and
that
2B~
is
hypercube
embeddable
if
t
2:
n;-2.
Lemma
25.2.5.
Let t
2:
1
be
an integer.
(i)
If
n
=f.
6, then
B~
is hypercube embeddable
if
and only
if
t
2:
n - 3.
(ii) For n
2:
6,
if
in;-2l
:::;
t
:::;
n - 4, then
B~
is a quasi h-distance.
Proof. (i)
Suppose
that
B;
is
hypercube
embeddable.
Then,
in
any
hypercube
embedding
of
B;,
we
can
suppose
that
each
point
i E
{I,
...
, n -
2}
is labeled
by
the
singleton {i} (as
the
metric
21
n
-2
is h-rigid
if
n
=f.
6).
This
implies
that
one
of
the
points
n -
1,
n
should
be labeled by a set A
containing
{I,
...
,n
-
2}
and,
thus,
IAI
- 1 = t
2:
n - 3.
(ii)
1ft
2:
in;-2l,
thenB~
is R1-embeddable. Hence,
ifn
=f.
6
and
in;-2l
:::;
t:::;
n-4,
then
B;
is a
quasi
h-distance.
If
n = 6
and
t = 2,
then
Bn
coincides
with
the
distance
d'f"
which is known
to
be a
quasi
h-distance. I
Given
n
2:
6, let
/tn
denote
the
distance on
Vn
defined by
/tn:=
8({1}) + 8({2}) +
3Si<jSn-l
-2
: 1'+
(n;-3)
,
= 1 +
(n;-4)
=n-4
=
2(n
-
5)
8(
{I,
2,
i,j}),
i.e.,
for 3
:::;
i
:::;
n -
1,
for 3
:::;
i
:::;
n - 1,
for 3
:::;
i < j
:::;
n.
For
instance, for n = 6,
/t6
coincides
with
the
path
metric
of
the
graph
K6
\P,
where P
:=
(1,6,2)
is a
path
on
three
nodes.
Lemma
25.2.6.
Let t, n
be
integers such that n
2:
6, n
=::
2
(mod
4), and
2t
2:
2 + (n;-3). Then, spht(/tn) is a quasi h-distance.
Proof.
It
is easy
to
see
that
the
condition
n
=::
2
(mod
4)
ensures
that
all
components
of
/tn
are
even integers, which implies
that
spht(/tn) E
en+!'
Let
F
denote
the
face
of
the
cone
CUTn
defined by
the
hypermetric
inequality
Q(b)Tx
:=
L.lSi<jsnbibjXij
:::;
0, where b
:=
(1,1,-I,
...
,-I,n
-
4)
E
~n
(with
n - 3
components
-1).
Set
S
:=
{I,
2,
Ii,
2i, 12i(3
:::;
i
:::;
n - 1),
12ij(3
:::;
i < j
:::;
n - I)},
(where
we
denote
the
sets
{1},{I,i}
by
the
strings
1,
Ii,
etc.).
The
nonzero
cut
semimetrics
satisfying
the
equation
Q(b)Tx
= 0 are 8(S) for S E
S,
which

390
Chapter
25.
Cut
Lattices, Quasi h-Distances
and
Hilbert
Bases
are linearly independent. Hence,
the
face F is a simplex face
of
CUT
n
.
As
the
distance
tLn
lies
on
F,
we deduce
that
/Ln
is
lrrigid
and
Sfl (tLn) = 2 +
(n;3).
Let G
denote
the
face
of
the
cone
CUT
n
+
l
defined by
the
hypermetric inequality
Q(b,
O)T
x
::;
OJ
the
nonzero
cut
semimetrics lying
on
G are li(
8),
li(8 U
{n
+
I}
)
for 8 E
Sand
li({n
+ I}). As 2t;::: sfl(tLn), spht(tLn) is
iI-embeddable
and,
in
fact, spht(tLn) lies
on
the
face G. Suppose
that
sph
t
(
d)
is hypercube embeddable.
Then,
there
exist nonnegative integers
"as,
/3s
(8
E S) such
that
asli(8) + /3sli(8 U
{n
+ I}).
Then,
ESES(as + /3s)li(8)
d,
which implies
that
as =
/3s
= 0 if 8
is
not
one
of
the
sets
{I}, {2}, {I,
2,
i,j},
and
{
ai
+
/3i
= 1
aij
+
/3ij
1
for i 1,2,
for 3
::;
i < j
::;
n -
1.
(setting
aij
= a12ij,
/3ij
=
/312ij).
Looking
at
the
component
of
spht(/Ln) indexed
by
the
pairs
(1, n + 1)
and
(2, n + 1),
we
obtain:
which implies
i,j
i,j
al
=
a2,/31
=
/32"
= t
La;;
1.
iJ
Looking
at
the
component
indexed by (i, n + 1) (3
::;
i
::;
n 1),
we
obtain:
;
i,j
j
Therefore,
o.
Summing
over i 3,
...
, n 1 yields
4(n -
5)
Laij
= (n -
3)(4/31
+ (n - 3)(n - 6)).
iJ
Looking finally
at
the
component indexed by
the
pair
(n, n + 1) yields:
and,
thus,
/31
+
/32
+ L
/3ij
+ , = t
i,j
(
n -
3)
2 + 1 =
O.

25.3 Hilbert Bases
of
Cuts
391
Using
the
fact
that
-::-;---=,{4l.11
+ (n - 3)(n - 6)),
we
deduce
that
2{3I
1, contradicting the fact
that
{3I
is integer. This shows
that
spht(/Ln) is not hypercube embeddable and, therefore, is a quasi h-distance.
I
25.3
Hilbert
Bases
of
Cuts
Let X be a finite set of vectors in Zk.
We
remind
that
Z(X),
114
(X)
and
Z+(X)
denote, respectively,
the
lattice,
the
cone and the integer cone generated by
X.
Clearly,
the
following inclusion holds:
The
set X is said to be a Hilbert basis
if
equality holds, i.e.,
if
Clearly, if X
is
linearly independent,
then
X is a Hilbert basis.
We
consider here
the
question
of
determining
the
graphs whose family
of
cuts is a Hilbert basis.
Given a graph
G
and
S
~
V,
the
cut
bG(S) consists
of
the
edges e E E with
one endnode
in
S and
the
other endnode
in
V \
S.
Let
KG
~
{O,
l}E
denote
the
family
of
the
incidence vectors
of
the
cuts
of
G. Then,
114
(KG) is called
the
cut
cone
of
G
and
it
is also denoted by CUT( G). Hence,
if
G is
the
complete
graph
Kn
on n nodes,
then
1I4(KK,.) =
CUT(K
n
)
coincides with
the
cone
CUT
n
.
Moreover,
the
integer cone
Z+(KK,,)
consists precisely of
the
distances on
Vn
that
are hypercube embeddable (recall Proposition 4.2.4).
We
are interested in
the
following problem:
Problem
25.3.1.
Let
1i
denote the class
of
graphs G whose family
of
cuts
KG
is a Hilbert basis. Identify the graphs G belonging to the family 1i.
We
review here what is known
about
the
class 1i. This problem will be revisited
in
Section 27.4.3
in
the
more general setting
of
binary matroids.
By
Theorem 24.1.3,
the
graphs K3, K
4
•
K5 belong to 1i.
On
the
other
hand,
the
graph Ks does not belong to
1i
(as
the
distance
2d(Ks
\e)
belongs
to
114
(KK/!J n Z(KKe)
but
not to
Z+(KKe))'
Moreover,
Proposition
25.3.2.
(i) Every graph with no K5
minor
belongs to
1i.
(ii) Every graph on at
most
six nodes and distinct from
Ks
belongs to
1i.

392
Chapter
25.
Cut
Lattices,
Quasi
h-Distances
and
Hilbert
Bases
(iii)
If
G belongs to 7t, then G does
not
have K6
as
a minor.
I
Assertion
(i)
in
Proposition
25.3.2 is
proved
in
Fu
and
Goddyn
[1995]
and
as-
sertions
(ii), (iii)
in
Laurent
[1996b].
The
proof
of
the
above
results
uses,
in
particular,
the
fact
that
the
class 7t is closed
under
certain
operations.
Namely,
(i)
7t is closed
under
the
clique
k-sum
operation
for
graphs
(k =
0,1,2,3).
(ii)
If
G E 7t
and
if
e is
an
edge
of
G,
then
the
graph
G/e
(obtained
by
contracting
the
edge e) belongs
to
7t.
(iii)
If
G E 7t
and
if
e is
an
edge
of
G for which each
inequality
v
T
x S ° defining
a facet
of
the
cut
cone
CUT(
G)
satisfies:
Ve
E
{O,
1,
-I},
L
vf
E
22
for all
cuts
bc(S),
fE6
a
(S)
then
the
graph
G\e
(obtained
by
deleting
the
edge e) belongs
to
7t.
For
instance,
Proposition
25.3.2 (iii)
can
be
checked
in
the
following way.
Suppose
that
G is a
graph
that
contains
K6 as a
subgraph.
Let x E
~E
be
defined by
Xe
= 2 for all edges
of
G
except
Xe
= 4 for one edge belonging
to
the
subgraph
K
6
•
Then,
x E
~(Kc)
n
Z(Kc)
(as x
can
be
extended
to
a
point
of
CUT
n n
en)
and
x
rf-
Z+(Kc)
(because
the
projection
of
x
on
K6 does
not
belong
to
Z+(KK6))'
Hence, every
graph
G E 7t does
not
contain
K6 as a
subgraph.
Proposition
25.3.2 (iii) follows, using
the
fact
that
7t is closed
under
contracting
edges.
The
complete
characterization
of
the
class 7t seems a
hard
problem.
This
is
partly
due
to
the
fact
that
the
linear
description
of
the
cut
cone is
not
known
for
general
graphs.
Many
questions
are
yet unsolved.
For
instance,
is
the
class 7t closed
under
the 6Y-operation
1
? A first
example
to
check is
whether
the
graph
from
Figure
25.3.3 belongs
to
7t
(this
is
the
graph
obtained
by
applying
once
the
6Y-operation
to
K
6
,
i.e.,
replacing
a
triangle
by
a claw
K
1
,3).
Figure
25.3.3:
6Y-transform
of
K6
Is
the
class 7t closed
under
the
deletion
of
edges?
(As
mentioned
above,
this
could
be
proved
only if a technical
assumption
is
made
on
the
facets
of
the
cut
cone.)
lLet
G
be
a
graph
having
a clique
on
the
nodes
u,v,
and
w.
The
ll.Y.operation
applied
to
this
clique
consists
of
removing
the
three
edges
uv,
uw,
vw
and
adding
a new
node
to
G
adjacent
to
each
of
the
three
nodes
u,
v,
and
w.

25.3 Hilbert Bases
of
Cuts
393
As
we
will see in Section 27.4.3,
the
question
of
characterizing
the
graphs
whose family of
cuts
is
a Hilbert basis
can
be posed in
the
more general framework
of
binary
matroids.
Another question of interest
is
to
determine a Hilbert basis for the
cut
cone
on
6 points;
this
is
the
smallest case when
the
cuts do
not
form a Hilbert basis.
In
fact,
the
following result holds, which
is
equivalent
to
Theorem 25.2.2.
TheoreIll
25.3.4.
The
31
nonzero cut semimetrics on
V6
together with the
15
metrics
2d(K
6
\e)
(Jar
e E
E(K6))
form a Hilbert basis. I
Finally, recall Proposition 25.1.10 which implies
that
the
16
odd
cuts
of
K6
form a
Hilbert
basis.
