Deza M.M., Laurent M. Geometry of Cuts and Metrics

354

Chapter

24. Recognition of

Hypercube

Embeddable

Metrics

all

of

them

even. For instance,

the

complexity

of

the

hypercube

embeddability

problem

for

the

class

of

distances

with

range

of

values {2,

4,

6}

is

not

known.

The

case

of

distances

taking

two even values

a,

b

is

also unsettled; Section 24.4

solves only

the

case when b = 2a.

We

start

in Section 24.1

with

some

preliminary

results.

24.1

Preliminary

Results

Let d be a distance on

the

set

V

n

.

A first easy observation

is

that

we

may

assume

that

no

pair

of

distinct

points

is

at

distance

O.

Indeed,

if

d(i,j)

= 0 for some

distinct

i, j E V

n

,

then

d is hypercube

embeddable

if

and

only

if

its

restriction

to

the

set

Vn

\ {j} is hypercube embeddable (as

the

points

i

and

j

should

be

labeled by

the

same

set

in any hypercube embedding

of

d).

If

d is

hypercube

embeddable,

then

(24.1.1)

d(i,j)

+ d(i, k) +

d(j,

k) E

2/2;

for all

i,j,

k E V

n

.

(Indeed,

if

AI,

.

..

,An

are sets forming

an

h-Iabeling

of

d,

then

d(i,

j)

+ d(i, k) +

d(j,

k) = 2(IAil +

IAjl

+ IAkl - IAi n

Ajl

- IAi n Akl -

IAj

n Akl) E

2/2;.)

The

condition

(24.1.1) is known as

the

parity condition;

it

was first

introduced

in

Deza [1960].

This

condition expresses

the

fact

that

each hypercube

embeddable

distance

don

Vn

can

be decomposed as

an

integer combination

of

cut

semimetrics,

i.e., belongs to

the

cut

lattice

en

(indeed, (24.1.1) characterizes

membership

in

en;

see

Proposition

25.1.1). As

an

application,

we

deduce

that

each

hypercube

embeddable

distance

has some

bipartite

structure,

namely,

the

set

of

pairs

at

an

odd

distance

forms a complete

bipartite

graph.

Lemma

24.1.2.

Let

d

be

a distance

on

V

n

.

If

d satisfies the

parity

condition

(24.1.1),

then

Vn

can

be

partitioned

into

Vn

=

BUT

in

such

a way

that

d(i,j)

is

even

ifi,j

E B

or

ifi,j

E

T,

and

d(i,j)

is odd

ifi

E

B,j

E

T.

I

This

simple fact will be central in

our

treatment.

For instance,

the

generalized

bipartite

metrics, considered

in

Section 24.2, have only one even distance equal

to

2,

i.e.,

they

satisfy

d(i,j)

= 2 for i

i=

j E B, i

i=

JET,

for some

bipartition

(B,

T)

of

V

n

.

Obviously, every

hypercube

embeddable

distance d

on

Vn

is

f\

-embeddable,

i.e., belongs

to

the

cut

cone CUTn- In

other

words, d

can

be decomposed as a

nonnegative

combination

of

cut

semimetrics. Hence,

we

have

the

implication:

d is

hypercube

embeddable

==}

d E

CUTn

and

d satisfies (24.1.1)

In general,

this

implication

is

strict.

But,

for some classes

of

distances,

this

implication

turns

out

to

be

an

equivalence;

this

is

the

case, for instance, for

the

distances

with

range

of

values

{1,2},

or

{I,

20:,

20:

+ I}

(0:

2:

2)

(see Proposi-

tions

24.1.9

and

24.1.10), or for

the

distances considered

in

Proposition

24.3.27

24.1 Preliminary Results

355

or

in

Theorem 24.5.1.

This

is also

the

case for

the

distances on n

::;

5 points, as

the

next result by Deza [1960,

1982]

shows.

Theorem

24.1.3.

Let

d

be

a distance on n

::;

5 points. Then, d is hypercube

embeddable

if

and

only

if

d E

CUT

nand

d satisfies the parity condition (24.1.1).

I

The

parity

condition (24.1.1) also suffices to characterize hypercube embeddabil-

ity for

the

distances

that

lie on specified facets of

CUT

n,

in particular, on several

classes

of

simplex facets; see relation (31.8.3).

We

will consider in

Chapter

25

the

quasi h-points, which are

the

distances d

that

belong to

CUTn

and

satisfy

(24.1.1)

but

are not hypercube embeddable.

Each valid inequality for the cut cone yields therefore a necessary condi-

tion

for hypercube embeddability.

It

turns out

that

the

hypermetric inequalities

will

playa

crucial role for

the

characterization

of

certain classes

of

hypercube

embeddable distances; see Propositions 24.1.9, 24.3.10, 24.3.11, 24.3.27. Hy-

permetric

inequalities have been introduced in Section

6.1

and studied in de-

tail in

Part

II;

we

recall here the main definitions

in

order to make

the

chap-

ter

self-contained. Let d be a distance on

Vn

and

let k

2:

1 be

an

integer.

Then,

d

is

said

to

be (2k +

l)-gonal

if,

for all (not necessarily distinct) points

iI,

...

, ik, ik+l,

jl

,

...

,jk

E V

n

,

the

following inequality holds:

(24.1.4)

Equivalently,

d is (2k + 1}-gonal if, for all b E

zn

with

"'-'Js,t:::,nb;

"'-'l<

••

<-n

Ibil

=

2k

+

1,

(24.1.5)

L

bibjd(i,j)::;

O.

lsi<jsn

1

and

Moreover, d is said to

be

hypermetric if d

is

(2k + 1 )-gonal for all k

2:

1.

The

inequality (24.1.4) is called

the

(2k + 1 )-gonal inequality.

We

now

recall

the

link existing between hypercube embeddable distances

and

intersection patterns. A vector p E

jRv"

UE"

is

called

an

intersection pattern

if

there exist a set n

and

n subsets

"41,

...

,An

of n such

that

(24.1.6)

Pij

IAi n

Aj

I for all 1

::;

i

::;

j

::;

n.

Hypercube embeddable distances are

in

one-to-one correspondence with inter-

section

patterns,

via

the

covariance mapping (see Sections 5.2

and

5.3 and,

in

particular, Proposition 5.3.5). Namely, for a distance

don

Vn+b d is hypercube

embeddable if

and

only

if

its image p =

~(d)

under the covariance mapping is

an

intersection

pattern

(indeed,

the

sets

AI'"''

An, An+l = 0 form

an

h-labeling

of

356

Chapter

24. Recognition of Hypercube

Embeddable

Metrics

d if

and

only if

AI,'

..

,An

satisfy (24.1.6)). Recall

that

p =

e(

d)

is defined by

{

Pii

=

d(i,n

+

1)

Pij =

~(d(i,

n + 1) +

d(j,

n + 1) -

d(i,j))

for 1

S;

i

S;

n,

for 1

S;

i < j

S;

n.

An

early reference

on

intersection

patterns

is

Kelly

[1968];

in

particular,

Kelly

characterizes

there

the

intersection

patterns

of order n

S;

4,

thus, providing an-

other

prooffor

Theorem

24.1.3.

The

above correspondence

permits,

for instance,

to

obtain

the

following result of

Chvatal

[1980]

(which will also follow from

the

treatment

in

Section 24.4).

Proposition

24.1.7.

The hypercube embeddability problem is polynomial

for

the class

of

distances with range

of

values

{2,

4}

and

having a

point

at distance

2

from

all

other

points.

Proof.

Let d

be

a distance

on

V

n

+

l

such

that

d(i, n +

1)

= 2 for all i E Vn

and

d(i,j)

E {2,4} for all i

oJ-

j E V

n

.

Its

image p =

e(d)

satisfies Pii = 2 for all

i E

Vn

and

Pij E

{O,

I} for all i

oJ-

j E V

n

. Let H denote

the

graph

on

Vn

with

edges

the

pairs

(i,j)

such

that

Pij =

1.

Then,

d is

hypercube

embeddable

if

and

only if p is

an

intersection

pattern

which,

in

turn,

is equivalent to H being a line

graph.

The

result now follows from

the

fact

that

line graphs

can

be recognized

in

polynomial

time

(Beineke [1970]). I

The

hypercube

embeddability

problem

is

hard

for general metrics;

this

was

shown by

Chvatal

[1980]

in

the

context of intersection

patterns.

Theorem

24.1.8.

The

hypercube embeddability problem is

NP-complete

for

the

class

of

distances having a

point

at distance 3 from all

other

points

and

with

distances between those points belonging to

{2,

4,

6}.

Proof.

We

sketch

the

proof. Let d be a distance as

in

the

theorem. Hence,

its

image p =

e(d)

satisfies Pii = 3 for all i E Vn

and

Pij E

{O,

I,

2}

for all i

oJ-

j E V

n

.

Let H denote

the

multigraph

with

node set

Vn

and

having Pij parallel edges

between nodes

i

and

j.

It

is

easy to see

that

d is

hypercube

embeddable, i.e., P

is

an

intersection

pattern,

if

and

only if

the

edge set

of

H

can

be

partitioned

into

cliques

in

such a way

that

each node belongs to

at

most

three

of these cliques.

Chvatal

[1980]

shows

that

the

problem of testing whether a 4-regular

graph

is

3-colourable (which

is

NP-complete)

can

be

polynomially reduced to

the

above

edge

partitioning

problem for H. I

There

are some classes of distances for which hypercube

embeddability

is

very easy to characterize. Here are two examples taken, respectively, from As-

souad

and

Deza

[1980]

and

Deza

and

Laurent

[1995a].

The

first example will be

contained

in

Proposition

24.3.10.

Proposition

24.1.9.

Let

d

be

a distance

on

Vn

with values

in

{1,2}. The

24.2 Generalized

Bipartite

Metrics

following assertions are equivalent.

(i)

d is hypercube embeddable.

(ii) d is 5-gonal

and

satisfies the parity condition (24.1.1).

357

(iii) d is the path

metric

of

the complete bipartite graphs

Kl,n~l

or Kz,z,

or

d =

2d(K

n

}.

I

Proposition

24.1.10.

Let

d

be

a

metric

on

Vn

with range

of

values {1,

20:,

20:+

1},

for

some

integer 0: ;::

2.

Then, d is hypercube embeddable

if

and

only

if

d

satisfies the parity condition

(24.1.1).

Proof. Suppose

that

d satisfies (24.1.1). Hence,

the

set

of

pairs

at

odd

distance

forms a complete

bipartite

graph

KS,T

for some

bipartition

(S,

T)

of V

n

.

As

0:

;::

2,

the

pairs

at

distance 1 form a matching, say,

d(i1,h)

=

...

=

d(ik,jk)

= 1

for

i1,""

ik

E

Sand

j1,'"

,jk

E

T.

Then,

d

O(S)

+

showing

that

d is

hypercube

embeddable.

iES\{il)···)ik}

jET\{}j,·

..

,h}

o:o({i}),

I

'The case

0:

1,

the

case

of

the

distances

with

range of values {1,

2,

3}, is

significantly more complicated

and

will be

treated

in Section 24.3.

We close

this

section

with

a result on

the

number

of distinct

hypercube

errlbE;(1dlml~S

of

a given distance. Given a

hypercube

embed

able distance d

on

Vn

and

an

integer s

2:

0,

let N

n

(

d,

s) denote

the

number

of

distinct

Z+-realizations

d

Aso(S)

(with

As

E

Z+)

of

d

with

size

Ls

As

=

s.

Set

where

the

sum

is

taken

over all s E

Z+

and

over all distances

don

Vn

satisfying

L1S,i<js,nd(i,j)

=

x.

It

is shown

in

Deza,

Ray-Chaudhuri

and

Singhi

[1990]

that

the

function x E

Z+

f-t

Afn(x}

is quasipolynomial.

In

other

words,

there

exist

an

integer t

;::

1

and

polynomial., fo,

II,

... ,

ft-1

such

that

Mn(X) = f;(x)

if.1:

==

i (mod t), for 0:-; i:-; t 1.

In

particular,

Mn(x)

is

bounded

by a polynomial

in

x. Therefore,

the

number

of

distinct

Z+-realizations of d

is

bounded

by a polynomial in x

d(i,j).

24.2

Generalized

Bipartite

Metrics

Let

d be a

metric

on

Vn

such

that

d(i,j)

= 2 for all i

:j:.

j E

Sand

i

:j:.

j

for some

bipartition

(S,

T)

of

V

n

.

Such a metric

is

called a generalized bipartite

metric.

The

lSI

x

ITI

matrix

D

with

entries

d(i,j)

for i E

S,j

E T is called

the

(S,

T)-distance

matrix

of

d.

For instance,

the

path

metric of a complete

bipartite

358

Chapter

24.

Recognition of Hypercube Embeddable Metrics

graph

is a generalized bipartite metric.

In

this

section,

we

prove

the

following

result, which is due

to

Deza and Laurent

[1995aJ.

Theorem

24.2.1.

The hypercube embeddability problem is polynomial-time solv-

able for the class

of

generalized bipartite metrics.

We

start

with

an

easy observation.

Lemma

24.2.2.

Let

d

be

a generalized bipartite metric with bipartition (8,

T).

If

d is hypercube embeddable, then there exists an integer

0'

such that

d(i,j)

E

{O',o'

+ 2,0' +

4}

for all i E

8,j

E

T.

Proof. Let

0',

(3

denote the smallest and largest value taken by

d(i,j)

for i E

8,j

E say

0'

d(i,j),

(3

dW,i')

for

i,i'

E

8,

i,j'

E

T.

Using

the

triangle

inequality,

we

obtain

(3

d(

i',

j')

:::;

d(

i', i) +

d(

i,

i)

+

d(j,j')

~

4 +

0'.

Moreover,

0',

(3

have the same parity by (24.1.1). I

We

will see below what are the possible configurations for the pairs

at

distance

0',0'

+ 2,0' +

4.

Set s

:=

181

and t

:=

ITI.

Let

ds

(resp. d

T

) denote the restriction of d to

the

set 8 (resp.

T).

Then,

ds

=

21.

and

dT

= 21t are equidistant metrics.

Recall (from Proposition 23.4.3)

that

the equidistant metric 21n is h-rigid if

n

'"

4

and

that

214 has exactly two Z+-realizations, namely, its

star

realization:

214

D(

{i}),

and

an

additional realization:

214

=

6(

{I,

2}) +

D(

{I,

3}) + D({I, 4}),

called here

the

special realization.

The

proof

of

Theorem 24.2.1 is based on

the

following simple observation.

Let

be a Z+-realization

of

d.

Then,

its projection on

8:

L

>'AD(A

n 8),

A<;;;V"

is a Z+-realization

of

ds. Hence,

if

8

'"

4,

then

it

must

coincide

with

the

star

realization of 218 and, if s = 4,

it

must coincide

with

the

star

realization or with

the

special realization of 21

4

•

The

same holds for d

T

•

The

following definitions will be useful in

the

sequel. A Z+-realization

of

d

is called a star-star realization

if

both

its

projections on 8

and

on T are

the

star

realizations

of

21.

and

21t,

respectively. A realization of d is called a star-special

realization if its projection on 8 is the

star

realization of

21.,

but

t 4

and

its

projection on T is the special realization

of

214' Finally, a realization

of

d is

called a

special-special realization if s t 4

and

both

its projections on 8 and

T are

the

special realization

of

214.

24.2 Generalized

Bipartite

Metrics

359

A'

G'

B'

D'

A

(f

+

2)J

a

f+2

f f

-

2I

a

G

f+2 f+2

f f

B f

f

(f

- 2)Jb

f-2

+2Ib

D

f f

f-2

Figure 24.2.3

We now analyze

the

structure

of

the

hypercube

embeddable

generalized bi-

partite

metrics

admitting

a

star-star

realization.

Proposition

24.2.4.

Let

d

be

a generalized bipartite

metric

with bipartition

(5,

T).

Then, d

admits

a

star-star

realization

if

and

only

if

there exist a parti-

tion

{A,

B,

G,

D}

of

5

and

a partition

{A',

B',

G',

D'}

ofT

(with possibly

empty

members)

with

IAI

=

IA'I

and

IBI

=

IB'I

and

there exist one-to-one mappings

(T

: A

---+

A'

and

r : B

---+

B'

and an integer f

2:

IBI

+

IDI

+

ID'I

such

that

the

values

d(i,j)

are given by

(24.2.5)

if

(i,j)

E

((A

U

G)

x

(B'

U

D'))

U

((B

U

D)

x

(A'

U

G'))

U{(k,(T(k)) IkE

A}

U

{(k,r(k))

IkE

B},

if

(i,j)

E

((A

U

G)

x

(A'

U

G'))

\

{(k,

(T(k)) IkE

A},

if

(i,j)

E

((B

UD)

x

(B'

x

D'))

\

{(k,r(k))

IkE

B}.

Proof.

Let

d be a generalized

bipartite

metric

admitting

a

star-star

realization:

d = L 8(U), where U

is

a collection (allowing repetition)

of

nonempty

subsets

UEU

of

V.

Hence,

IU

n

51

E

{a,

s,

1,

s -

I}

and

IU

n

TI

E

{a,

t, 1, t -

I}

for all U E U.

We

can

suppose

without

loss

of

generality

that

lun51

E

{a,

I}

for all U E U. Let

M

denote

the

matrix

whose columns are

the

incidence vectors

of

the

members

of

U. Combining

the

above

mentioned

two possibilities for

Un

5

with

the

four

possibilities for

Un

T,

we

obtain

that

M has

the

form shown in

Figure

24.2.6.

Hence

the

sets A,

B,

G,

D

and

A',

B',

G',

D'

form

the

desired

partitions

of

5

and

T.

We

can

now

compute

d(i,j)

for

(i,j)

E 5 x T

and

verify

that

they

satisfy

relation

(24.2.5),

after

setting

f

:=

IBI

+

IDI

+

ID'I

+

m.

Conversely, suppose

that

d is defined by (24.2.5). Set A = {Xl,

...

,x

n

}

and

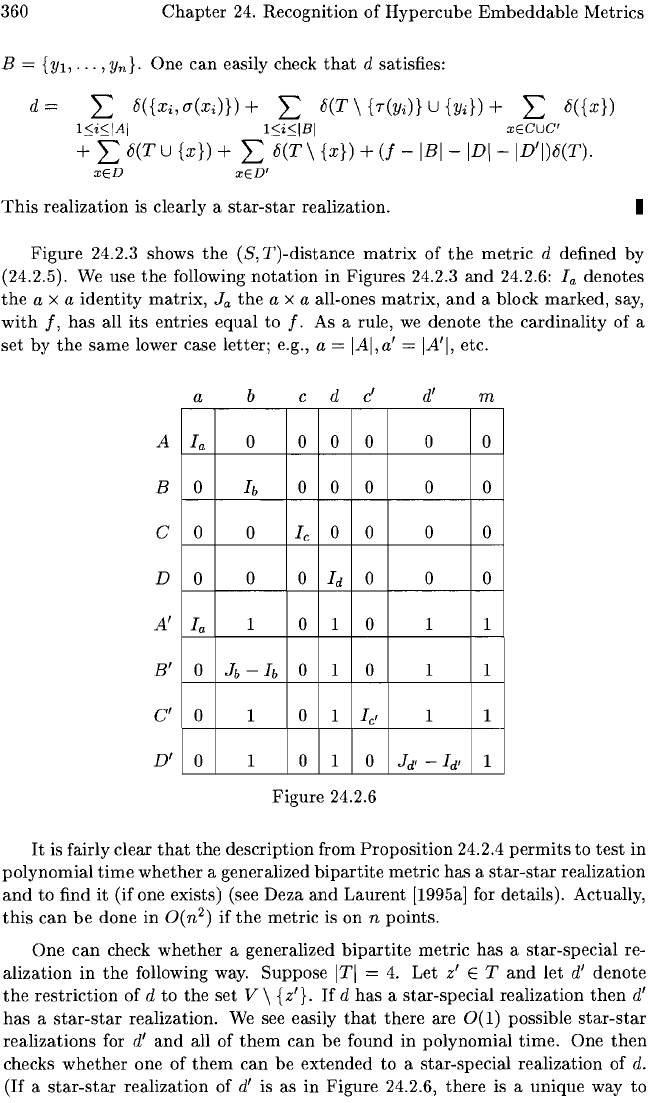
360

Chapter

24.

Recognition

of

Hypercube

Embeddable

Metrics

B =

{Yb

...

,Yn}'

One

can

easily check

that

d satisfies:

d = L 8({Xi,0'(Xi)}) + L 8(T \ {r(Yi)} U

{yd)

+ L 8({x})

l~i~IAI l~i~IBI

xECUC'

+ L

8(TU

{x})

+ L

8(T\

{x})

+U

-IBI-IDI-ID'I)8(T).

xED'

This

realization

is

clearly a

star-star

realization.

I

Figure

24.2.3 shows

the

(8,

T)-distance

matrix

of

the

metric

d defined by

(24.2.5). We use

the

following

notation

in Figures 24.2.3

and

24.2.6:

Ia

denotes

the

a x a identity

matrix,

J

a

the

a x a all-ones

matrix,

and

a block marked, say,

with

f,

has

all

its

entries equal to f. As a rule,

we

denote

the

cardinality of a

set

by

the

same

lower case letter; e.g., a =

IAI,a'

= IA'I, etc.

a

b

cdc'

d'

m

A

Ia

0 0 0 0

0

B 0

h

0 0 0 0 0

C 0

0

Ie

0 0 0 0

D

0

0 0

Id

0 0 0

A'

Ia

1

0

1

0

1 1

B'

0

Jb

-h

0

1

0

1 1

C'

0 1 0 1

Ie'

1 1

D'

0

1 0 1

0

J

d

, - I

d

,

1

Figure

24.2.6

It

is fairly clear

that

the

description from

Proposition

24.2.4

permits

to

test

in

polynomial

time

whether

a generalized

bipartite

metric has a

star-star

realization

and

to find

it

(if one exists) (see Deza

and

Laurent

[1995a] for details). Actually,

this

can

be

done in

0(n

2

)

if

the

metric is on n points.

One

can

check

whether

a generalized

bipartite

metric has a star-special re-

alization in

the

following way. Suppose

ITI

=

4.

Let z' E T

and

let d'

denote

the

restriction

of d to

the

set V \

{z'}.

If

d

has

a star-special realization

then

d'

has

a

star-star

realization. We see easily

that

there

are

0(1)

possible

star-star

realizations for d'

and

all of

them

can

be

found in polynomial time.

One

then

checks

whether

one

of

them

can

be

extended to a star-special realization of

d.

(If

a

star-star

realization of

d'

is as in

Figure

24.2.6,

there

is a

unique

way to

24.2

Generalized

Bipartite

Metrics

361

complete

it

to

a star-special realization

of

d,

namely, by adjoining the following

row as a

last

row

to

Figure

24.2,6,)

Finally, a generalized

bipartite

metric d has a special-special realization if

and

only if, for some m E Z+, the (5, T)-distance

matrix

of

the

semimetric

d -

mli(T)

is one

of

the nine matrices from Figure

24.2.7

(up to

permutation

on

5

and

T). (This fact can

be

checked, using a characterization

of

the

general-

ized

bipartite

metrics

admitting

a special-special realization analogous

to

that

of

Proposition

24,2.4, see Deza and Laurent [1995aJ.)

3 1 1 1

1 3 1 1

1

131

1 1 1 3

444

2

422

2

4 2 2 2

2 2 2 0

2

224

2

224

2 2 2 4

0

2 2

2

2 0 2 2

2

2 0 2

2

2 2 0

3 1

1 1

1

3

1 1

3 3 3

1

3 3

1 3

4 4 4 2

2 2 2

0

Figure

24.2,7

1

1 3

1 3 3

3

1 3 3 3

3 3 3 5

0 2 2 2

2 0 2 2

2 2 2 4

2 2 4 2

3 3 3 1

3 3 3

1

5 5 5

3

Example

24.2.8.

Given

an

integer k

;:::

5, let d

2

k

denote

the

metric defined

on

2k

points

by: d2k(i,

i+k)

4 for any 1

SiS

k

and

d

2

k(i,j)

= 2 for all

other

pairs

(i,j),1

S i

i=

j S 2k. Hence, d

2

k

is a generalized

bipartite

metric

with

biparti-

tion

(

{I,

2

...

, k},

1,

k +

2,

...

, 2k}). Note

that

td2k is

the

path

metric of

the

cocktail-party

graph

Kkx2.

The

metric

d2l,

can

be

obtained

from the

equidistant

metric using

the

full

antipodal

extension operation, as

d2k

= Ant4(21k),

It

is

an

easy exercise

to

verify, for instance using

the

above procedure,

that

d

2k

is

not

hypercube

embeddable

(another

proof

of

this fact has been given

in

Section 7,2,

see

Example

7.2.7).

On

the

other

hand, one verifies easily

that

d

2

k

belongs to

the

cut

cone CUT2k

and

to

the

cut lattice

£.2k

(see also Example 7.2.7). I

The

same

technique could be used for testing hypercube embeddability for

other

metrics

than

generalized

bipartite

metrics. Let d be a semimetric

on

V

n

.

Suppose

that

there

exists a

bipartition

(S,

T)

of

V such

that

the

projections d

s

and

d

T

of

d

on

Sand

T

are

of

the

form:

362

Chapter

24.

Recognition

of

Hypercube Embeddable Metrics

(24.2.9)

"ES

.,ET

for some positive integers

a."

(3".

From

Theorem

22.0.12, we know

that

ds

and

dT

are

h-rigid

if

lSI

is

big enough with respect

to

ma.x"ES

a",

and

if

ITI

is big enough with

respect

to

ma.x"'ET

(3",.

So, theoretically, one could use

the

same technique

as

the

one used

in

Proposition

24.2.4 for

studying

hypercube embeddability

of

these metrics. However,

a precise analysis

of

the

structure

of

the

distance

matrix

of

such metrics seems

to

be

technically much more involved

than

in

the

case considered above where all

a""

(3"

are

equal

to

1-

The

to

consider after

the

case

of

generalized

bipartite

metrics

would

be

the

class

of

metrics d for which

d(x,y)

4 for x #

yES

and

d(x,y)

= 2

for

x #

yET

(i.e., all

a,,'s

are

equal

to

2

and

all

(3,,'s

to

1).

One

can characterize

h-embeddability

of

these metrics by a similar reasoning as was applied

to

generalized

bipartite

metrics

and,

as

a consequence, recognize

them

in polynomial time. Indeed,

the

metric

41

n

is rigid for n 3

and

n

2:

9 and

41n

has exactly three Z+-realizations: its

star

realization

and

two special ones, for each n E

{4,5,6,

7,8}

(d.

Proposition 23.4.4).

Another

relatively simple case

is

when

one

of

the

sets S

or

T is small.

Deza

and

Laurent

[1995a] give a complete characterization

of

the

hypercube embeddable metrics

satisfying (24.2.9)

in

the

case

ITI

::;

2.

24.3

Metrics

with

Few

Values

In

this section,

we

consider the distances taking two values with distinct parities,

and the distances taking three values, not all even and one

of

them

being

the

sum of

the

other two. Namely, given

a,

bE

Z+,

we

consider the following classes

of

distances

d:

(a) d takes

the

values

2a,

b,

with b odd,

(b)

d takes

the

values

a,

b,

a +

b,

with

a,

b odd,

(c)

d takes

the

values

2a,

b,

2a

+

b,

with b odd and b <

2a,

and

(d)

d takes

the

values

2a,

b,

2a

+

b,

with b odd and

2a

<

b.

Laurent

[1994]

shows

that

the hypercube embeddability problem can be solved

in polynomial time within each

of

these classes.

Theorem

24.3.1.

For fixed

a,

b,

the hypercube embeddability problem within

each

of

the classes (a), (b), (c), (d)

can

be

solved in polynomial time.

We

sketch

the

proof

of

Theorem 24.3.1 in the rest of the section.

It

turns

out

that

each

of

the classes (a), (b), (c), (d) has

to

be treated separately.

The

instance a b = 1 of

the

class (c) was considered by Avis [1990j, who showed

that

the

hypercube embeddable distances with range of

,,-alues

{I,

2,

3}

can be

recognized in polynomial time. The prooffor the class (c) is essentially

the

same

as in

the

subcase a = b = L

The basic steps

of

the

proof are as follows. Let d be a distance on Vn from one

of

the

classes (a), (b), (c), or (d). One first checks whether d satisfies

the

parity

condition (24.1.1).

If

not, then d

is

not hypercube embeddable. Otherwise, let

24.3 Metrics

with

Few Values

363

(S,

T)

be

the

partition

of

Vn

provided

by

Lemma

24.1.2

with,

say,

lSI

2:

ITI.

Set

n(a,

b)

:=

a

2

+ a + 3

if

d belongs

to

the

classes (a), (c),

or

(d),

and

n(a,

b)

:=

(~?

+

~

+ 4

if

d belongs

to

the

class (b).

Ifn

<

2n(a,

b)-I,

then

one

can

test

directly

whether

d is

hypercube

embeddable,

for

instance,

by

brute

force

enumeration

(the

number

of

operations

in

this

step

depends

only

on

a,

b,

but

may

be

exponential

in

a,

b).

If

n

2:

2n(a,

b)

- 1,

then

lSI

2:

n(a,

b).

Hence,

the

restriction

of

d

to

the

set S

is

an

h-rigid

equidistant

metric. Therefore,

the

points

of

S

should

be

labeled

by

the

star

embedding

(or

an

equivalent

of

it)

in

any

h-Iabeling

of

d.

For

the

classes (a), (b), (c), (d),

this

information

enables us

to

completely characterize

the

hypercube

embeddable

distances

on

n

2:

2n(a,

b)

- 1

points

by

a set

of

conditions

that

can

be

checked

in

polynomial

time.

We

present

below these characterizations for

the

classes (a), (b)

and

(c); see

Propositions

24.3.8, 24.3.16, 24.3.18,

and

24.3.27. We

do

not

present

here

the

results

on

the

characterization

of

hypercube

embeddability

for

the

class (d), as

they

involve

too

many

technical details.

We also have some

partial

results for

the

characterization

of

the

hypercube

embeddable

distances

on

n points, for n

arbitrary.

See

Propositions

24.3.9,

24.3.10, 24.3.11,

and

24.3.17.

As

mentioned

above, we refer

to

Laurent

[1994]

for

the

study

of

the

class

(d).

Characterization

of

hypercube

embeddability

within

the

class (d) needs

many

technical conditions.

In

some subcases, one needs conditions involving

the

existence

of

some designs, namely,

of

intersecting

systems

with

prescribed

parameters.

Consider, for instance,

the

distance

d from

Figure

24.3.2.

One

can

check

that,

if

lSI

2:

a

2

+ a + 3,

then

d is

hypercube

embeddable

if

and

only

if

lUI

.::;

f(2a,

a;

a + b), i.e.,

if

there

exists a (2a, a)-intersecting

system

on

Va+b

of

cardinality

lUI.

s

~

U

Figure

24.3.2

distance

~

0

..

b

.....

0

o 2a

o

24.3.1

Distances

with

Values

2a, b

(b

odd)

Let

a, b

be

positive integers

with

b

odd.

Let

d

be

a

distance

on

Vn

with

range

of

values

{2a,

b}.

Suppose

that

d is a semimetric

and

satisfies

the

parity

condition

(24.1.1).

Then,

b

2:

a

and

let

(S,

T)

be

the

partition

of

Vn

provided by

Lemma

24.1.2.

Then

an

h-Iabeling

of

d consists of two

set

families A

and

B such

that

Deza M.M., Laurent M. Geometry of Cuts and Metrics

Подождите немного. Документ загружается.