Deza M.M., Laurent M. Geometry of Cuts and Metrics
Подождите немного. Документ загружается.


364
Chapter
24. Recognition
of
Hypercube
Embeddable
Metrics
(24.3.3)
{
A
is a
(b,
b -
a)-intersecting
system,
8 is a (2a,
a)-intersecting
system,
IAnBI
= a for all A E
A,B
E
8,
IAI
= lSI,
181
=
ITI
- 1.
Indeed,
label
a
point
jo E T by
0,
the
remaining
points
of
T by
the
members
of
8,
and
the
points
of
S by
the
members
of
A.
Lemma
24.3.4.
(i)
If
ITI
= 1,
then
d is hypercube embeddable.
(ii)
If
b
2:
2a,
then
d is hypercube embeddable.
(iii)
If
b < 2a
and
2
~
ITI
~
lSI
~
2a
a
_b
+ 1,
then
d is hypercube embeddable.
(iv)
If
b < 2a
and
d is hypercube embeddable,
then
min(ITI,
ISI-
1)
~
L
2a
b
_
b
J.
Proof.
For
(i), (ii),
and
(iii), we
construct
two families
A,
8 satisfying (24.3.3).
In
the
three
cases, we
take
for A a
A-system
with
parameters
(b,b
-
a)
and
center
AD,
IAol
= b - a.
In case (i),
take
simply 8 =
0.
In case (ii),
as
b
2:
2a, we
can
find a
subset
Bo
of
AD
with
IBo
I = a.
Then,
we
take
for 8 a
A-system
with
parameters
(2a, a)
and
center
Bo
such
that
(A
\ AD) n
(B
\ Bo) = 0 for all A E
A,
B E
8.
In
case (iii), we have a
2:
(s -
I)(2a
-
b)
(setting
s
:=
lSI), i.e., for each A E
A,
we
can
find s - 1 disjoint
subsets
A(1),
...
,
A(s-I),
of
A \ AD, each
of
cardinality
2a -
b.
Note
that
x
:=
b - a +
s(2a
-
b)
~
2a.
Let
X(1),
...
,
X(s-I)
be
disjoint
sets
of
cardinality
2a -
x,
disjoint from
UAEA
A.
Given
Al
E
A,
we
set
8
:=
{B(l),
...
,
B(s-l)}
where, for
I~j~s-I,
u
AEA\{A,}
Then,
A,
8 satisfy (24.3.3).
(iv)
Suppose
that
min(ITI,
ISI-
1)
2:
L2a
b
_
b
J +
1.
Let
k
be
an
integer such
that
min(ITI,
ISI-
1)
2:
k
2:
l2a
~
bJ + 1.
Set
b
i
= 1 for k + 1
points
of
S,
b
i
=
-1
for k
points
of
T,
and
b
i
= 0 for
the
remaining
points
of
V
n
.
Then,
L
bibjd(i,j)
=
2k(k(2a
-
b)
-
b)
>
O.
i,jEV
n
Hence, d violates a
(2k
+
I)-gonal
inequality
and,
thus,
is
not
hypercube
embeddable.
w
Figure
24.3.5
Figure
24.3.6
Figure
24.3.7
distance
o 2a
0
a-----L-o
I

24.3 Metrics
with
Few Values
365
Proposition
24.3.8.
Let
a
~
b
be
positive integers with b odd.
Let
d
be
a distance on n
points with range
of
values {2a, b}.
If
n
~
2a
2
+
2a+
5,
then
d is hypercube embeddable
if
and only
if
(i) d satisfies (24.1.1) and b
~
2a
or
(ii) d is the distance from Figure 24.3.5.
Proof.
Remains
to
show
the
"only
if'
part.
Suppose
that
d is hypercube embeddable
and
b < 2a. Let A
and
B satisfying (24.3.3).
By
assumption,
we
have
lSI
~
a
2
+ a + 3.
Hence, A
is
a
(b,
b system
with
IAI
~
a
2
+ a + 3.
By
Lemma
23.1.11,
A is a
ll-system;
let Ao be its center,
IAol
b a.
If
ITI
~
2,
then
IBI
~
1. Let B E B
and
set
a
IB
n Aol.
Then,
IB n
(A
\
Ao)1
= a - a for all A
EA.
Therefore,
2a
IBI
~
o+IAI(a-a)
aIAI-a(IAI-l)
~
aIAI-(b-a)(IAI-l)
=
(2a-b)IAI+b-a,
which implies
IAI
~
3a b
2a
a b +
1.
This
contradicts
the
fact
that
IAI
lSI
~
a
2
+ a +
3.
Therefore,
ITI
= 1, i.e., d is
the
distance from
Figure
24.3.5. I
Proposition
24.3.9.
Let
a
~
b
be
positive integers with b odd and b
~
2a.
Let
d
be
a distance on n points with range
of
values
{2a,b}.
Then d
is
hypercube embeddable
if
and only
ifd
satisfies (24.1.1). I
Proposition
24.3.10.
Let
a
~
b
be
positive integers
w·ith
b odd and b <
~a.
Let
d
be
a
distance with range
of
values {2a, b}. The following assertions are equivalent.
(i)
d
is
hypercube embeddable.
(ii) d satisfies the parity condition (24.1.1) and the 5-gonal inequality (i.e., d does
not
contain as substructure the distance from Figure 24.3.7).
(iii) d is one
of
the distances from Figures 24.3.5 and 24.3_6.
Proof.
The
implication (ii)
==>
(iii) follows from Lemma 24.3.4 (iv), after noting
that
L
2
"b_bJ
= 1 if b <
~a.
The
distance from Figure 24.3.6 (i.e.,
the
case
lSI
IT!
2)
is indeed hypercube embeddable; label
the
two nodes
of
T by 0
and
A U
A',
and
the
two nodes of S by
Ao
U A and
Ao
U
A',
where Ao,
A,
A'
are disjoint sets of respective
cardinalities
b - a, a, a. I
Note
that
Proposition
24.1.9
is
the
case a = b = 1
of
Proposition 24.3.10. So,
we
have a complete characterization
of
the
hypercube embeddable distances with values in
{2a,b}
(b
odd)
except when
a,b
satisfy:
~a
~
b < 2a.
24.3.2
Distances
with
Values
a,
b,
a + b (a,b
odd)
Let
a, b be positive
odd
integers with a <
b.
Let d be a distance on
Vn
with range
of
values
{a,
b,
a + b}. Suppose
that
d is a semirnetric
and
satisfies
the
parity condition (24.1.1).
Let (S,T) be
the
bipartition
of
V,..
provided by
Lemma
24.1.2. Hence,
d(i,j)
a+b
for
i
oF
j E
S,i
oF
JET,
and
d(i,j)
E
{a,b}
for i E
S,j
T.
Moreover,
the
pairs
ij
with
d(i,j)
= a form a matching.
Proposition
24.3.11.
If
there are at least two pairs at distance a, then the following
assertions are equivalent.
(i)
d is hypercube embeddable.
(ii) d satisfies (24.1.1) and the 5-gonal
ineq'ILality.

366
Chapter
24. Recognition
of
Hypercube
Embeddable
Metrics
(iii) d is the distance from Figure 24.3.12.
Proof.
Let
i,i'
E
8,
j,j'
E T such
that
d(i,j)
=
d(i',j')
= a.
If
there
exists k E
Vn
\
{i,i',j,j'},
then
set b
i
bi'
bk
= 1, b
j
= bj' =
-1,
and
bh
= 0 for
the
remaining
points.
Then,
i.e., d violates a 5-gonal inequality. This shows (ii) =::;> (iii).
If
V" =
{i,i',j,j'}
then
d
is indeed hypercube embeddable; let A
and
B be disjoint sets with
IAI
= a
and
IBI
= b
and
label i by
_4,
i'
by
B,
j by
0,
and
j'
by
Au
B. This shows (iii) =::;> (i). I
IX
'·':,
'.,
I><l'.,
. : :
: :
i
~
1
° 0
Figure 24.3.12 Figure 24.3.13
0,
~"",""'/'/
\if
Figure 24.3.14
distance
°
a+b
0
o
From now on,
we
can suppose
that
there
is
exactly one pair
(io,jo)
at
distance a,
where
io
E
8,
jo E
T.
In an h-labeling
of
d,
we
can
suppose
that
io
is
labeled by 0
and,
then,
io
should
be
labeled by a set
-40
of
cardinality
a.
Therefore,
an
h-labeling
of
d
exists if
and
only if
there
exist two set families A
and
B such
that
(24.3.15)
{
A,
Bare
(b,
b-t)
-intersecting systems,
IA
n
BI
=
~
for all
_4
E A,
BE
B,
An
Ao
= B n
-40
= 0 for all A E A, B E B,
IAI
==
181
-
I,
IBI
= ITI-1.
Indeed, label
the
points
of
8 \
{io}
by
the
members
of
A
and
the
points
of
T \ {io} by
Ao
U B where B E
B.
Proposition
24.3.16.
Let a < b
be
odd
integers and let d
be
a
di.sta.nce
on n
2:
2(
~?
+ a + b + 7 points with range
of
values {a,
b,
a +
b}
which
is
not the distance
from Figure
24.3.12. Then, d
is
hypercube embeddable
if
and only
if
d is the distance
from Figure 24.3.14.
Proof.
The
distance from Figure 24.3.14 is hypercube embeddable; indeed choose for A
a fl.-system. Conversely, suppose
that
d
is
hypercube embeddable.
By
assumption,
Hence,
A
is
a
(b,
)-iIlltel'se(:tiIllg
system with
By
Lemma
23.1.11, A
is
a fl.-system; let
Al
be its center, lAd =
b;a.
Suppose
that
ITI
2:
2
and
let B E
B.
Then,
IB
n
(A
\
Adl
2:
a for all
_4
E
A,
implying b =
IBI
2:
alA!,
in contradiction
with
the
above assumption
on
IAI.
Therefore,
ITI
= 1, i.e., d is
the
distance from Figure 24.3.14. I
24.3 Metrics
with
Few Values
367
Proposition
24.3.17.
Let a, b
be
odd integers such that a < b < 2a. Let d
be
a distance
with range
of
values {a,
b,
a + b}. Then, d is hypercube embeddable
if
and only
if
d is
one
of
the distances from Figures 24.3.12, 24.3.13, and 24.3.14.
Proof.
Suppose
that
d is
hypercube
embeddable
and
that
d is
not
the
distance
from
Figure
24.3.12. Set k
:=
min(ITI,
lSI
- 1).
If
k
~
2,
then
k
::;
l~J
(else, d violates
a (2k
+ 1)-gonal inequality). Hence, k = 1, which implies
that
d is
the
distance
from
Figures
24.3.14
or
24.3.13. I
24.3.3
Distances
with
Values
b,
2a, b +
2a
(b
odd,
b < 2a)
Proposition
24.3.18.
Let
a, b
be
positive integers with b odd and b < 2a. Let d
be
a
distance on n
~
2a
2
+ 2a + 5 points with range
of
values {2a,
b,
2a + b}. The following
assertions are equivalent.
(i) d is hypercube embeddable.
(ii) d is a
semimetric,
d satisfies (24.1.1) and d does
not
contain as substructure any
of
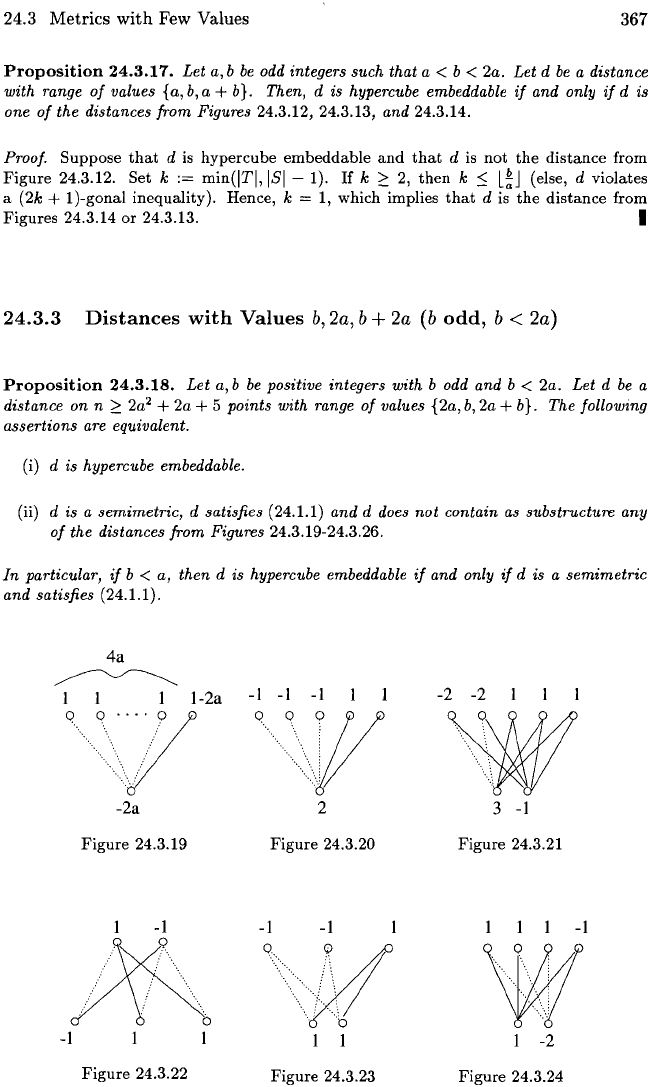
the distances from Figures 24.3.19-24.3.26.
In
particular,
if
b < a, then d is hypercube embeddable
if
and only
if
d is a
semimetric
and satisfies (24.1.1).
4a
~
I I I 1-2a
-I -I -I
-2 -2
Q Qy
·····6
q
-2a 2
3 -I
Figure
24.3.19
Figure
24.3.20
Figure
24.3.21
-I
-I
-I
WV
..........
\\j
-I
-2
Figure
24.3.22
Figure
24.3.23
Figure
24.3.24

368
Chapter
24. Recognition of Hypercube
Embeddable
Metrics
2 2
-1
-1
-3
Figure
24.3.25
Figure
24.3.26
In
Figures
24.3.19-24.3.26, a plain edge
represents
distance
2a+b, a
dotted
edge
distance
b
and
no
edge
means
distance
2a.
Proof. For
the
implication
(i)
===>
(ii), we check
that
none
of
the
distances
from
Figures
24.3.19-24.3.26 is
hypercube
embeddable.
Indeed,
the
distances
from Fig-
ures 24.3.19-24.3.25 violate
some
hypermetric
inequality.
The
numbers
assigned
to
the
nodes in
Figures
24.3.19-24.3.25
indicate
a choice
of
integers bi's for which
the
hyperme-
tric
inequality
(24.1.5)
is
violated. For
instance,
for
the
distance
from
Figure
24.3.19,
L
b;bjd(i,j)
= 4a(2a(2a -
b)
-
b)
~
4a > 0
i,jEV
n
since 2a - b
~
1.
The
distance
from
Figure
24.3.26
is
not
hypercube
embeddable
by
Proposition
24.3.8
(and
its
proof).
We show
the
implication
(ii)
===>
(i). As d satisfies
the
parity
condition,
Vn
is
partitioned
into
SUT
with
lSI
~
ITI,
d(i,j)
=
2a
for (i,
j)
E
S2
UT2,
d(i,
j)
E {b, b+ 2a}
for
(i,j)
E S x
T.
Set
s:=
lSI. For
JET,
set
NbU)
:=
{i E S I
d(i,j)
= b}.
For
v E
{0,1,2,
...
,s
-l,s},
set
We
group
below several
observations
on
the
sets Tv.
(i) T
s
-
I
= 0 (since d does
not
contain
the
configuration from
Figure
24.3.19).
(ii)
ITs
I :::: 1 (since d does
not
contain
the
configuration from
Figure
24.3.26).
(iii) All
Tv
are
empty
except
maybe
To,
T
I
, T
2
,
Ts
(indeed, INbU)1
::::
2
or
INbU)1
~
s L 1
for all
JET,
since d does
not
contain
the
substructure
from
Figure
24.3.20).
(iv)
At
least
one
of
To
and
T2
is
empty
(since d does
not
contain
the
substructure
from
Figure
24.3.21).
(v)
If
ITII
~
2,
then
(vI)
either
all
NbU)
U E
Td
are
equal,
(v2)
or
all
NbU)
U E
Td
are
distinct
(since d does
not
contain
the
substructure
from
Figure
24.3.22).
(vi)
If
j i-
j'
E T
2
,
then
INbU)
n NbU')1 = 1 (use
Figures
24.3.22
and
24.3.23).
(vii)
If
j E
TI
and
j'
E T
2
,
then
NbU)
n
NbU')
i- 0 (by
Figure
24.3.22).
(viii)
If
b < a,
then
T2
=
Ts
= 0 (by
the
triangle
inequality).
We show how
to
construct
an
h-Iabeling
of
d.
Let
Ai
(i E
S)
be
disjoint sets
of
cardinality
a.
Set
A
:=
UiESA
i
.
Label
the
elements
of
S
by
the
Ai'S.

24.3 Metrics
with
Few Values
369
Suppose
first
that
b < a.
Then,
by (viii),
d(il,jtl
=
...
=
d(i"jr)
= b for
some
i
l
,
...
,iT E S,
jl,'"
,jr
E
T,
1
::;
r
::;
IT!-
Let
X,
E
j
(j
E T \
{jl,
...
,jr})
be pairwise
disjoints
sets
that
are
disjoint from A
and
satisfy
IXI
=
b,
IE
j
I = a.
Label
jl,'
..
,
jT
by
Ail
U
X,
...
,Air
U
X,
respectively,
and
JET
\
{jl,'"
,jr}
by
Xu
E
j
.
This
gives
an
h-labeling
of
d.
We now
suppose
that
b
~
a.
Let
X
be
a
set
disjoint from A
with
IXI
= b - a.
-
If
Ts
oF
0
then
Ts
=
{x}
(by (i)); label x by
X.
-
Label
each
element
j E
T2
by
UiENb(j)
Ai
U X (this gives
already
an
h-labeling
of
the
projection
of
d
on
S U
Ts
U
T2
(by (vi))).
-
Suppose
that
all Nb(j)
(j
E T
I
)
are
equal
to,
say, {io},
as
in (vI).
Let
Yj
(j
E
Ttl
be
pairwise disjoint
sets
that
are
disjoint from A
and
X
and
have
cardinality
a.
Label
j E
TI
by
Ai
o
U X U Yj.
If
all Nb(j)
(j
E
Ttl
are
distinct
as in (v2),
then
label j E
TI
by
UiENb(j)
Ai
U X U
Y,
where
Y is a
set
disjoint from A
and
X
with
WI
= a.
(In
both
cases, we have
obtained
an
h-labeling
of
the
projection
of
d
on
S U
Ts
U
T2
uTI
(by (vii)).)
-
Suppose
that
To
oF
0.
Then,
T2
= 0 by (iv).
Let
Zk (k E
To)
be
pairwise disjoint
sets
that
are
disjoint from all
the
sets
constructed
so
far
and
have
cardinality
a.
If
we
are
in
case
(vI),
then
ITII
::;
1
or
(ITII
::;
2
and
ITol
= 1). (Indeed, if
ITII,
IT21
~
2,
then
d
contains
the
substructure
from
Figure
24.3.25
and,
if
ITII
~
3,
ITol
= 1,
then
we
have
the
substructure
from
Figure
24.3.24.)
If
lTd = 1,
TI
=
{j},
label
kETo
by X U Yj U Zk.
If
ITII
= 2,
TI
= {j, j/},
then
label
the
unique
element
kETo
by
Xu
Yj U Yj,.
Else, we
are
in case (v2).
Then,
label
kETo
by X U
YU
Zk.
In
both
cases, we have
constructed
an
h-labeling
of
d.
I
Observe
that
the
exclusion
of
the
distance
from
Figure
24.3.26 is used only for show-
ing
that
ITsl
::;
1, i.e.,
that
at
most
one
point
is
at
distance
b from all
points
of
S.
Consider
the
distance
d
s
on
s + 2
points
which has
the
same
configuration
as in Fig-
ure
24.3.26
but
with
s nodes on
the
top
level
instead
of
a
2
+ a + 3.
Let
s(a,
b)
denote
the
largest
integer
s such
that
d
s
is
hypercube
embeddable.
Then,
Proposition
24.3.18 re-
mains
valid if we exclude
the
distance
ds(a,b)+l
instead
of
excluding
the
distance
d
a
'+a+3
from
Figure
24.3.26.
Note
that
a 2
2::;2a_b+1::;s(a,b)::;a
+a+2,
with
s(a,b)
= 2 if b <
~a
(use
Proposition
24.3.10).
This
implies
the
following
result.
Proposition
24.3.21.
Let
a, b
be
positive integers with b odd and b <
~a.
Let
d
be
a
distance
on
n
~
2a
2
+ 2a + 5 points with range
of
values {2a,
b,
2a + b}. The following
assertions are equivalent.
(i)
d is hypercube embeddable.
(ii) d is
i't
-embeddable and satisfies (24.1.1).
(iii) d is hypermetric and satisfies (24.1.1).
(iv) d satisfies (24.1.1) and the (2k + 1)-gonal inequalities for
2k
+ 1 =
5,7,11,
8a-1.
(v) d is a
semimetric,
d satisfies (24.1.1), and d does
not
contain
as
substructure
any
of
the distances from Figures 24.3.7 and 24.3.19-24.3.25. I
Note
that
Proposition
24.3.27
is
a
direct
extension
of
the
result
given in Avis [1990]
for
the
subcase
a = b = 1.

370
Chapter
24. Recognition
of
Hypercube
Embeddable
Metrics
24.4
Truncated
Distances
of
Graphs
We consider here
the
hypercube embeddability problem for
the
distances
taking
two values
of
the
form a, 2a, where a
~
1
is
an
integer. Such distances
can
be
interpreted
as scale multiples
of
truncated
distances
of
graphs. Indeed, for a
distance
d
on
V
with
values a, 2a,
let
G = (V,
E)
denote
the
graph
with
edges
the
pairs
at
distance a.
Then,
d coincides
with
ade,
where
de
is
the
truncated
distance
of
G
(taking
value 1 on
an
edge
and
value 2
on
a
nOn
edge).
(The
truncated
distance has already been considered earlier in
Chapter
17.)
As
we
see here,
the
hypercube
embeddability
problem
can
be solved in poly-
nomial
time
for
the
class
of
distances
with
values a, 2a.
The
case
when
a is
odd
has
already
been
settled
in
the
previous section (cf.
Proposition
24.3.10).
Namely, such distances are hypercube embeddable
if
and
only
if
they
satisfy
the
parity
condition (24.1.1)
and
the
pentagonal
inequalities. Hence,
it
suffices
to
verify
that
all subspaces
on
at
most
five
points
are hypercube
embeddable
in or-
der
to
ensure
that
the
whole distance space
is
hypercube embeddable. A
similar
finite
point
criterion has been discovered by Assouad
and
Delorme [1980, 1982]
in
the
case
when
a
is
even.
The
proof
uses again as a basic tool
the
fact
that
some
equidistant
submetrics
are h-rigid,
but
the
details are more involved
in
this
case.
Theorem
24.4.1.
Let
(X,
d)
be
a finite distance space with runge
of
values
{2k,4k}
where k
~
1 is an integer.
SetNk:=
(3M
2
R+R+2M
2
)(M+1)+8k+4,
where M
:=
4k2 +
4k
+ 3 and R denotes the
Ramsey
number
r(M,
M).
Then,
(X,
d)
is hypercube embeddable
if
and
only
if
(Y,
d)
is hypercube embeddable
for
every
subset
Y
~
X with
WI
::;
Nk·
The
value
of
Nk
given in this
theorem
could certainly be improved
(at
the
cost
of
a more detailed analysis). For instance, Assouad
and
Delorme
[1980]
show
that,
in
the
case k =
1,
N2
can be replaced by 120.
The
value given here suffices,
however, for
the
purpose
of
demonstrating
polynomial-time solvability.
The
rest
of
the
section
is
devoted to
the
proof
of
Theorem
24.4.1. We intro-
duce some
notation.
For convenience,
we
visualize a distance d
On
V
with
values
2k,4k
as d =
2kd
e
,
where G =
(V,
E)
is
the
graph
with
edges
the
pairs
at
dis-
tance
2k.
Then,
isometric subspaces
of
(V,
d)
correspond to
induced
subgraphs
of
G.
Then
we
introduce
the
class
of
graphs
f"k
which consists
of
the graphs G
for which
2kd
e
is
hypercube
embeddable.
Our
aim
is
to show
that
a
graph
G
belongs
to
f"k
whenever all
its
induced
subgraphs
on
at
most
Nk nodes belong
to
f"k.
It
is convenient
to
formalize this notion. A class C
of
graphs is said to
have
order
of
congruence
2
p if C
is
closed
under
taking
induced
sub
graphs
and
'We
remind
that,
given
integers
s,
t
~
1,
the
Ramsey
number
res,
t)
denotes
the
smallest
integer
n
such
that
every
graph
on
n
nodes
contains
either
a
clique
of
size s
or
a
stable
set
of
size t.
Some
estimations
for
res,s)
are
known; for
instance,
2t
:s;
r(s,s):S;
c:-=-n.
(Cf., e.g.,
Bondy
and
Murty
[1976].)
2The
notion
of
order
of
congruence
has
already
been
introduced
earlier;
it
is, however,
used

24.3 Metrics
with
Few Values
371
if a
graph
belongs
to
C whenever all its induced
subgraphs
on
at
most
p nodes
belong
to
C,
and
p is
the
smallest such integer.
Thus,
we
have
to
show
that
f"k
has
order
of
congruence::;
N
k
. For this,
we
decompose
f"k
into two subfamilies
9k
and
f"k
\
9k
whose orders of congruence are easier to determine. Namely, let
9k
denote
the
class of
graphs
G satisfying, either (i)
VG
E
f"k'
or (ii) G E
f"k
and
G
is
a suspension
graph
(i.e., has a node adjacent
to
all
other
nodes). We
will also consider a class
11k
(to
be
described later) such
that
f"k
\
9k
<:;;
11k
<:;;
f"k.
Then,
the
main
steps
of
the
proof
consist of showing
that
(i)
9k
has order
of
congruence::;
8k
+
4,
(ii)
11k
has
order of congruence::;
(3M2
R + R +
2M2)(M
+ 1).
The
result
from
Theorem
24.4.1 follows
in
view
of
the
following (easy)
lemma.
Lemma
24.4.2.
Let
A
and
B
be
families
of
graphs
having
respective orders
of
congruence
a
and
b.
Then,
Au
B has order
of
congruence::; a +
b.
I
We now
determine
the
order of congruence of
9k
and
the
next subsection will
study
the
order
of
congruence
of
11k.
Proposition
24.4.3.
The
family
9k
has order
of
congruence::;
8k
+ 4.
Proof. Define
Ik
as
the
subfamily of
9k
consisting
of
the
graphs G whose sus-
pension
VG
belongs
to
f"k.
In
a first step,
we
show
that
(a)
Ik
has order
of
congruence
::;
4k
+
2.
For this, let G =
(V,
E) be a
graph
such
that
G[X] E
Ik
for all X
<:;;
V
with
IXI
::;
4k
+
2;
we
show
that
G E
Ik,
i.e.,
that
VG
is hypercube
embeddable
with
scale 2k. We
can
assume
without
loss of generality
that
G is connected.
By
the
assumption,
we
know
that
VG
is
ll-embeddable
(as
4k
+ 2
?:
6
and
the
family
of
graphs
whose suspension
is
ll-embeddable
has
order
of
congruence 6 by
Theorem
17.1.8). Therefore, G
is
a line
graph
or a
subgraph
of
a cocktail-party
graph
(again by
Theorem
17.1.8).
If
G
is
a line
graph
we
are done, since
2d;c
is
hypercube
embeddable. Hence, G is contained in a cocktail-party
graph
K
nx2
.
We
can
assume
without
loss of generality
that
G has exactly one
pair
of
opposite
nodes.
In
other
words, G =
Kn+1
\e
and
2kd;c
= ant4k(2klLn+l). Let c(k)
denote
the
largest integer such
that
ant4k(2k:D.c(k))
is
hypercube embeddable.
Then,
c(k)
::;
4k + 1 by
Theorem
23.3.1 (i). Hence, G E
Ik
if
n + 1
::;
c(k).
On
the
other
hand,
if n
?:
c( k)
then
we
can
choose a subset X of V of size
c(k) + 1
containing
both
end
nodes of
the
deleted edge
e.
Now G[X] E
Ik
since
IXI
::;
4k
+
2.
This
implies
that
ant4k(2klLc(k)+1)
is
hypercube embeddable,
contradicting
the
definition
of
c(k). Hence, (a) holds.
We
can
now proceed
with
the
proof. Let G =
(V,
E)
be a
graph
such
that
G[X] E
9k
for all
IXI
::;
8k
+
4;
we
show
that
G E
9k.
We
can
suppose
that
G
if-
Ik,
else
we
are done. By (a),
there
exists Y
<:;;
V
with
WI
::;
4k
+ 2
such
here
in
a
more
restrictive
sense.

372
Chapter
24. Recognition of
Hypercube
Embeddable
Metrics
that
C[Y]
rt
I
k
, i.e.,
VC[Y]
rt
Fk. For
any
Z
~
V
with
IZI
:::;
4k
+
2,
we
have
that
C[YU
Z] E Yk, which implies
that
C[YU
Z] is a suspension
graph
with
apex
node
Z E
Y.
Then,
C is a suspension
graph
with
apex
y E
Y.
(For,
suppose
that
for every y E Y
there
exists
Zy
E Z not
adjacent
to
Yj
then
a
contradiction
is
reached by considering
Z
:=
{Zy
lyE
Y}.)
One
can
now verify
that
C[V
\ {y}]
belongs
to
Ik
with
the
help of (a).
This
shows
that
C E Fk
and,
thus,
C E Yk.
I
Next, we consider
the
class Fk \ Yk. Some
further
definitions are needed. We
remind
that
M
:=
4k
2
+
4k
+ 3
and
R =
r(M,
M)
is
the
Ramsey
number.
Let
C =
(V,
E)
be
a
graph.
We
call M -clique (resp. M -stable set)
any
maximal
clique (resp.
stable
set) of size
2:
M.
Then,
Vo
denotes
the
union
of all
M-
cliques
and
V
1
denotes
the
union
of
their
pairwise intersections. A
subset
L
~
Vo
is called transversal
if
C[L]
is connected
and
L
meets
every
M-clique
in
at
most
one
point.
Finally, V
2
denotes
the
union of
the
transversals
that
have a node
adjacent
to
a node of V \
Vo.
We now
introduce
the
class
'Hk
which consists of
the
graphs
C E
Fk
satisfying
the
following
conditions
(i)-(vi):
(i)
C
has
no M -stable set.
(ii)
C
has
at
most
M
distinct
M-cliques.
(iii)
Any
two
distinct
M -cliques
meet
in
at
most
two points.
(iv) A node
adjacent
to
4 nodes of
an
M-clique K belongs
to
K.
(v)
C[L]
is a complete
graph
for every
transversal
L.
(vi)
Maximal
transversals
are pairwise disjoint.
Note
that,
for a
graph
satisfying (i)-(vi),
IV
\
Vol:::;
R (by
the
definition of
Vo
and
R),
1V11
:::;
M2,
and
1V21
:::;
3M2R.
We show
in
the
next
subsection
that
Fk \
Yk
is contained
in
'Hk
and
we
study
the
order
of congruence of
'Hk.
24.4.1
The
Class
of
Graphs
Hk
Our
aim
here is
to
show
that
Fk
\ Y k
~
'Hk
and
to
determine
the
order
of
congruence of
'Hk.
In
what
follows, C =
(V,
E)
is a
graph
in
Fk
\ Yk. Hence,
2kd'G
can
be
isometrically
embedded
into
some
hypercube
H(n).
That
is,
there
is a
mapping:
xEVt->x~n
such
that
IXL::.YI =
2k
if
xy
is
an
edge
and
IXL::.YI
=
4k
otherwise. (We will use
below
the
same
letters
x
and
X for
denoting
a node of C
and
the
subset
labeling
it
in
the
hypercubej
we
may
sometimes identify
both
notions
and
speak
of node
X.)
We will use
the
following fact
(cf.
Theorem
22.0.6 or 23.1.9):
The
sets Y
labeling
the
nodes y of
an
M -clique K form a
~-system
(because M =
4k
2
+

24.3 Metrics
with
Few Values
373
4k + 3).
That
is,
there
exists a set C
such
that
C
<;;;
Y,
IY \
CI
= k for all y E K
and
the
sets
Y \ C are pairwise disjoint;
the
set
C is called
the
center
of
the
M-clique
K.
A
similar
result
holds for
M-stable
sets (as M
~
k
2
+ k + 3).
Lemma
24.4.4.
G has
no
M -stable set.
Proof.
Suppose, for contradiction,
that
S is
an
M-stable
set.
We
can
assume
without
loss
of
generality
that
the
nodes
yES
are
labeled
by
pairwise disjoint
sets
Y,
each
of
cardinality
2k.
We
claim:
(a)
Every
node x E V \ S is
nonadjacent
to
some node
of
S.
For,
suppose
that
x E V \ S is
adjacent
to
all nodes
of
S.
Then,
x is
labeled
by
X = 0 (by
the
pentagonal
inequality applied
to
the
nodes Y
1
,
Y
2
,
Y
3
E S, X
and
0).
This
implies
that
x is adjacent
to
all nodes
of
G,
contradicting
the
fact
that
G
f/.
(h.
Indeed, let x' E V \ S (X'I- x)
be
labeled
by
X';
if
IX'I
= 4k
then
lSI:::;
4 (since IX'L::"YI
:::;
4k implies
that
IX'
nYI
~
k for each
yES).
Therefore,
(a) holds.
Let
x E V \ S
be
labeled
by
X
and
let
yES
which is
not
adjacent
to
x;
thus,
IX
L::"YI
= 4k.
Then,
2k
:::;
IXI
:::;
6k
(by
the
triangle
inequality
applied
to
0,X,Y).
If
IXI
>
2k
then
IX
n YI =
~(IXI
- 2k) > 0 for every
node
yES
nonadjacent
to
x;
hence,
IXI
~
lSI
- 2 >
6k
since x
can
be
adjacent
to
at
most
two
nodes
of
S (by
the
pentagonal
inequality). Therefore,
IXI
= 2k. So, we have
found a
hypercube
embedding
of
2kd
VG
(labeling
the
apex
node
by
0).
This
contradicts
the
assumption
that
G
f/.
(h.
I
Lemma
24.4.5.
Let
K
be
an M -clique
with
center
C
and
let x E V \ K
be
labeled by
X.
Then,
IXL::"CI
= 3k.
Proof.
By
the
maximality
of
K,
there
exists y E K which is
not
adjacent
to
x;
so
IX
L::"YI
= 4k.
Thus,
3k
:::;
IX
L::"CI
:::;
5k
(by
the
triangle
inequality
applied
to
X,
Y,
C).
Clearly,
IX
L::"CI
=
3k
if
x is
adjacent
to
some y E
K.
Suppose
now
that
x is
not
adjacent
to
any
y E
K.
Then,
for y E
K,
4k
=
IXL::"YI
=
I(X
L::"C)L::"(CL::,,Y)
I
and,
thus,
IXL::"CI-
3k
= 21(X \ C) n
(Y
\ C)I.
This
implies
that
IXL::"CI
=
3k
(else
IX
\
CI
~
M). I
Lemma
24.4.6.
Two
distinct
M-cliques
meet
in
at
most
two points.
Proof.
Suppose
that
Yl,
Y2,
Y3
are
distinct
elements
in
two
distinct
cliques
K,
K'
with
respective centers
C,
C'.
The
pentagonal
inequality
Q(I,
1,
1,
-1,
-If
x:::;
o
applied
to
the
distance
on
the
points
Y
1
,
Y
2
,
Y
3
,
C,
C'
(assigning 1
to
Y
1
,
Y
2
,
Y
3
and
-1
to
c,
C') implies
that
C = C'.
This
contradicts
the
triangle
inequality
applied
to
C = C', Y E K \
K'
and
Y'
E
K'
\
K.
I
Lemma
24.4.7.
Let
K and
K'
be
distinct
cliques with respective
centers
C
and
C'.
Then,
I
CL::"C'
I = 2k.
