ДеМерс Майкл Н. Географические информационные системы. Основы

Подождите немного. Документ загружается.

достаточно времени. Может оказаться более легким использование

отдельных карт

на

каждую

из

тем, чтобы символы

не

накладывались

и не

мешали. Короче говоря,

данной ситуации нужно нечто большее,

чем то,

что может дать простое наложение САПР.

Топологическое

векторное

наложение

Топологическая структура данных, представленная

Главе

позволяет

программе отслеживать пространственные связи между объектами.

Она также определяет метод наложения полигональных покрытий,

обеспечивающий передачу многих атрибутов объектов полигонам

результирующего покрытия. Этот топологический результат, известный как

наименьшая географическая единица

(least common geographic

unit

(LCGU))

[Chrisman

and Puecker,

1975],

придуман

для

показа того,

как

изменения

полигональных объектов могут достичь пункта,

за

которым невозможно

дальнейшее деление.

этими наименьшими единицами деления

связывается набор атрибутов, который также

не

может далее делиться

на

категории.

По

сути,

это

деление имитирует описанный выше метод

МакХарга, когда упомянутый набор атрибутов определяет степень черноты

области, соответствующей уровню чувствительности окружающей среды.

мы

увидим,

как

топология помогает проводить наложение

векторных покрытий, рассмотрим несколько примеров, после чего сравним

выполнение наложения

векторных

растровых системах.

Векторные

наложения

"точка

полигоне"

и "линия

полигоне"

Хотя большинство векторных

ГИС

ориентированы

на

выполнение

операции наложения полигонов,

мы

можем рассмотреть некоторые шаги

по компьютеризации векторных наложений "точка

полигоне"

"линия

полигоне". При этом мы будем подразумевать, что покрытия имеют общую

систему координат. Программа должна уметь определять положения точек

или линий относительно границ полигонов,

которыми мы их сравниваем.

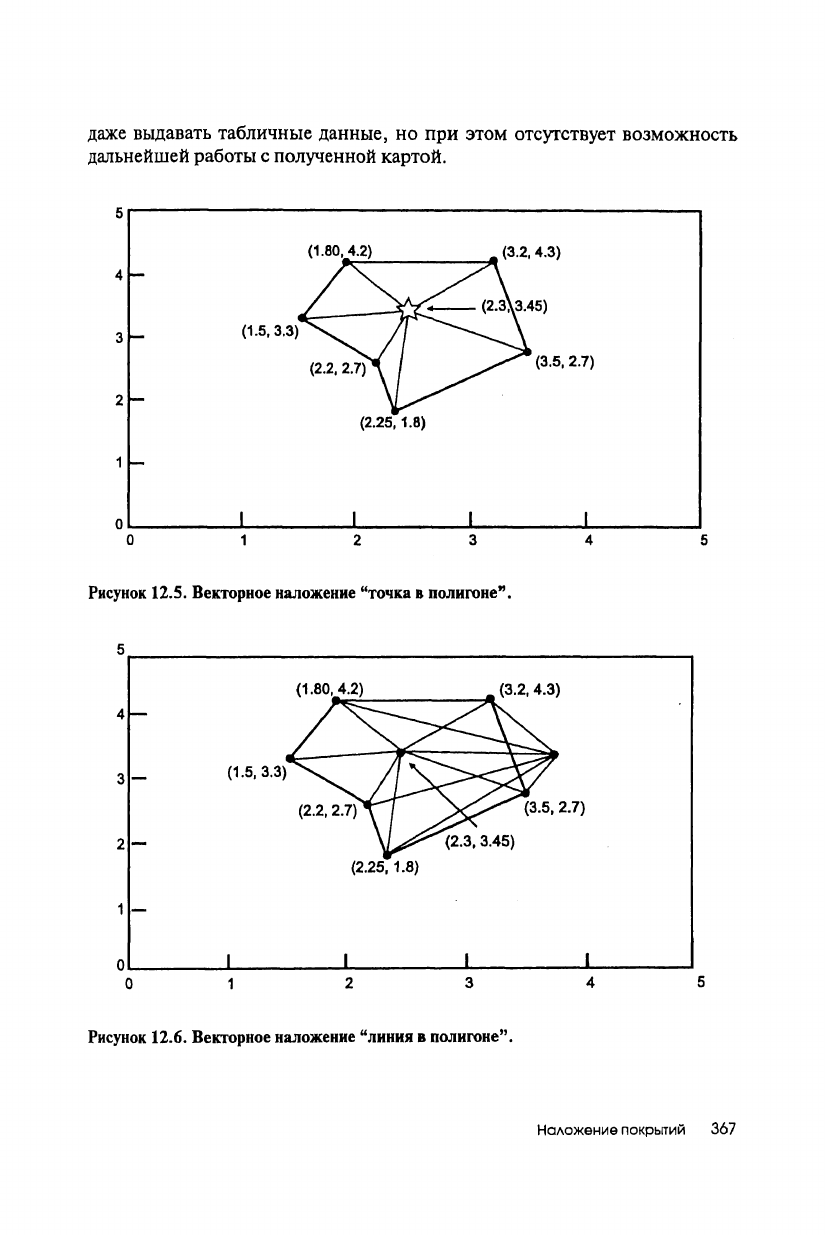
Рисунок

12.5

иллюстрирует определение принадлежности точки

координатами

(2.3, 3.45)

изображенному полигону.

Такое наложение может выполняться с целью создания нового покрытия,

состоящего только из тех полигонов, которые содержат указанные точки*.

Существует одна проблема,

которой могут столкнуться пользователи

некоторых ГИС. Хотя такие системы могут проводить рассматриваемые

наложения, они

не

могут сохранять

их как

отдельное покрытие. Они могут

* Или другой

вариант -

только

из тех точек,

что

принадлежат указанным полигонам. Говоря

общем,

операция наложения разнородных объектов несимметрична

алгебраическом смысле.

— прим. перев.

даже выдавать табличные данные, но при этом отсутствует возможность

дальнейшей работы с полученной картой.

(1.80,

4.2)

(3.2,

4.3)

(2.з\з.45)

—

(1.5,

3.3)^4.

/1^

(2.2,2.7)4

(3.5,

2.7)

(2.25,1.8)

I I

0 1 2 3 4 5

Рисунок 12.5. Векторное наложение "точка в полигоне".

(1.80,

4.2)

(3.2,

4.3)

(1.5,3.3)^4.

/I \

(2.2,

2.7^Y|

\^^3.5, 2.7)

—

'ф.Х

3.45)

(2.25,1.8)

I I

I 1

0 1 2 3 4 5

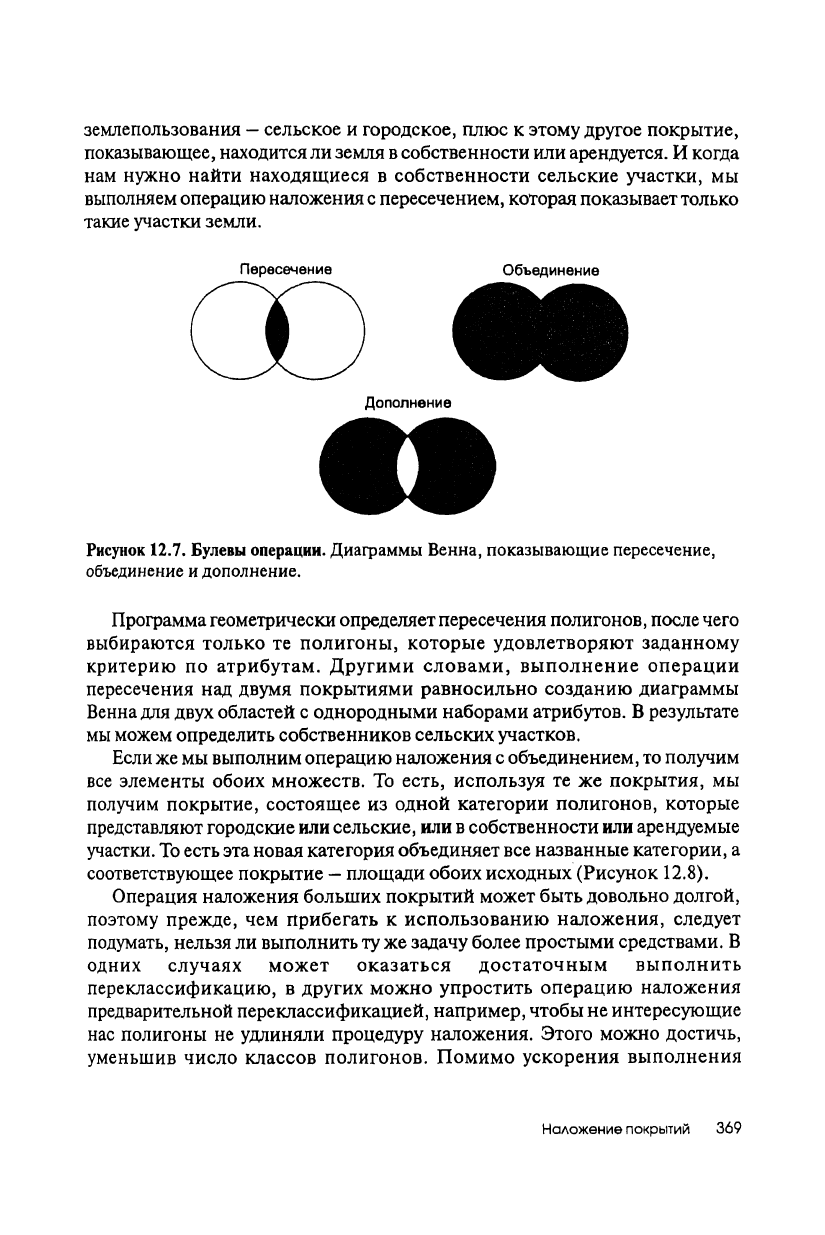
Рисунок 12.6. Векторное наложение "линия в полигоне".

Это ограничение является обычно следствием того, как система хранит

связанную с графикой табличную информацию, впрочем, техническое

объяснение не подходит для данного курса, и часто причины не так уж важны

для пользователя. В качестве выхода из этой ситуации можно предложить

создание очень маленьких буферов (выглядящих как точки на выходной

карте),

которые становятся крошечными полигонами. Это покрытие можно

сохранить, и точки будут представляться его микрополигонами.

Наложение "линия в полигоне" заключается в соотнесении координат

концевых и промежуточных точек линии с границей полигона с целью

определения принадлежности этих точек полигону, то есть, по сути оно

сводится к выполнению нескольких точечных наложений. Дополнительным

моментом является то, что линия может пересекать границу полигона. В

простейшем случае можно считать, что если хотя бы одна точка линии

принадлежит полигону, то и вся линия принадлежит ему. Но более

корректным подходом является определение точек пересечения линии с

границей полигона и создание в них узлов, что позволит разделить атрибуты

внутренних и внешних по отношению к полигону частей линии. Например,

если лесозащитная полоса как линейный объект пересекает границу между

пашней и лугом, мы сможем сказать, какая часть полосы принадлежит

каждой изобластей, а также создать таблицу, показывающую это отношение.

Как видите, векторные наложения "точка в полигоне" и "линия в

полигоне" являются вопросом не только графического отношения объектов,

но и отношения атрибутов. В конце концов, объекты карты представляют

часть реального мира.

Векторное

наложение

полигонов

Для векторного наложения полигонов, подобно случаю "линия в

полигоне", программа должна определить точки пересечения границ

полигонов одного покрытия с границами полигонов другого покрытия.

Эти точки пересечения становятся узлами, и программа отслеживает

передачу атрибутов в новое покрытие.

Поскольку многие векторные ГИС связаны с СУБД, не удивительно, что

булева логика, используемая в запросах к БД, используется также и для

пространственных запросов. На самом деле булево наложение

(Boolean

overlay)

является широко распространенным подходом. Его легко понять,

особенно если вы уже знакомы с операциями над множествами. Эти

операции часто иллюстрируются так называемыми диаграммами Венна

(Рисунок

12.7).

В случае булева векторного наложения мы сравниваем не сами атрибуты,

а пространство, занимаемое каждым из двух наборов атрибутов. Допустим,

у нас есть простое покрытие, имеющее только два типа полигонов

землепользования

—

сельское и городское, плюс к этому другое покрытие,

показывающее, находится ли земля в собственности или арендуется. И когда

нам нужно найти находящиеся в собственности сельские участки, мы

выполняем операцию наложения с пересечением, которая показывает только

такие участки земли.

Пересечение

Объединение

Рисунок

12.7.

Булевы

операции.

Диаграммы

Венна,

показывающие

пересечение,

объединение

и дополнение.

Программа геометрически определяет пересечения полигонов, после чего

выбираются только те полигоны, которые удовлетворяют заданному

критерию по атрибутам. Другими словами, выполнение операции

пересечения над двумя покрытиями равносильно созданию диаграммы

Венна для двух областей с однородными наборами атрибутов. В результате

мы можем определить собственников сельских участков.

Если же мы выполним операцию наложения с объединением, то получим

все элементы обоих множеств. То есть, используя те же покрытия, мы

получим покрытие, состоящее из одной категории полигонов, которые

представляют городские или сельские, или в собственности или арендуемые

участки. То есть эта новая категория объединяет все названные категории, а

соответствующее покрытие - площади обоих исходных (Рисунок

12.8).

Операция наложения больших покрытий может быть довольно долгой,

поэтому прежде, чем прибегать к использованию наложения, следует

подумать, нельзя ли выполнить ту же задачу более простыми средствами. В

одних случаях может оказаться достаточным выполнить

переклассификацию, в других можно упростить операцию наложения

предварительной переклассификацией, например, чтобы не интересующие

нас полигоны не удлиняли процедуру наложения. Этого можно достичь,

уменьшив число классов полигонов. Помимо ускорения выполнения

наложения это позволяет сделать результат наложения более простым и

контролируемым.

Покрытие,

образованное

объединением

двух

других

покрытий

Рисунок 12.8. Наложение с объединением. В результате этой операции мы получаем

покрытие всей изучаемой области, включающее все четыре категории земли.

В заключение данной темы вернемся к идее идентифицирующего

наложения. В этом случае мы можем получить результаты, сходные с ранее

приведенными примерами, за исключением того, что при использовании

булевых операций для выполнения реального картографического наложения

мы помним об атрибутах. Таким образом, получающиеся в результате

полигоны показывают комбинации всех пересекающихся полигонов.

Другими словами, мы выполняем наложение графических фигур и заносим

в таблицу все комбинации категорий. Так, например, если у нас есть четыре

различные категории, пересекающиеся в пространстве (скажем,

землепользование, типы почвы, сообщества животных и типы

растительности), то все они будут занесены в таблицу. Следовательно, мы

можем иметь полигон, который содержит фруктовый сад

(землепользование), чернозём (тип почвы), мыши-полевки (сообщество

животных) и орех-пекан (тип растительности). Имея все эти тематические

наборы данных и зная соотношения между ними, мы легко можем

определить численность представителей одной категории из других. Многие

операции наложения выполняются для получения такой статистики.

Замечание

об

ошибках

при

наложении

Простые булевы и идентифицирующие наложения, созданные главным

образом для данных номинальной шкалы, малопригодны для данных других

шкал измерения. Нам же часто приходится иметь дело с числовыми

данными, которые дают больше возможностей наложения, обеспечиваемых

теми же математическими операциями, что и в алгебраическом растровом

наложении. Любая полнофункциональная СУБД позволяет выполнять

алгебраические действия над данными таблиц атрибутов, связанных с

графикой карты. Благодаря этому процесс наложения даже более лёгок, чем

в простейших растровых системах, и практически идентичен реализации в

растровых системах, использующих СУБД.

Алгебраическое наложение в векторных системах выполняется во многом

так же, как и в растровых, если не считать добавочные операции с

векторными графическими фигурами. Это сходство окажется очень

полезным, когда мы будем рассматривать картографическое моделирование

в следующей главе. Но результаты наложения в растре и векторах могут

выглядеть по-разному: в векторной системе могут неожиданно оказаться

десятки и даже сотни мелких полигонов, особенно вдоль границ

пересекающихся полигонов. Эти визуально незначительные расхождения

могут существенно влиять на результаты анализа.

В качестве примера рассмотрим сравнение двух равномасштабных

покрытий землепользования, созданных на основе двух аэрофотоснимков

одного участка земной поверхности в моменты времени Т

{

и Т

При

сравнении двух внешне одинаковых покрытий оказывается, что они

совпадают не точно, что приводит к образованию осколочных полигонов

вдоль границ накладываемых полигонов (Рисунок

12.9).

Перед нами встает

вопрос: вызвано ли это реальными изменениями в промежуток между двумя

моментами съемки или причина кроется в погрешностях съемки и/или

оцифровки? Интуиция подсказывает, что столь малые изменения

землепользования маловероятны, особенно учитывая то, что сами полигоны

выглядят столь похожими, а даже небольшие изменения в самом

землепользовании дали бы гораздо более значительные изменения картины.

Осколочные

полигоны,

созданные

операцией

наложения

Полигон Полигон

Наложение

момент

T1 в

момент

Т2

полигонов

Рисунок 12.9. Осколочные полигоны, созданные векторным наложением. Небольшие

различия (будь то вследствие ошибок или реальных изменений) в целом почти

одинаковых полигонов приводят к возникновению осколочных полигонов. Это

следует учитывать, если малые отклонения важны для анализа.

Игнорируя микроскопические изменения

земле, шьзовании,

мы

пытаемся разобраться

причинах несовпадения полигонов.

Сами полигоны могут быть одинаковой формы,

но при

этом чуть-чуть

повернутыми.

Мы

можем попытаться устранить этот поворот, однако даже

при самом тщательном исполнении редко удается достичь полного

совпадения.

тому

же,

такой поворот зачастую может привести

рассогласованию других полигонов. Короче говоря, здесь

нет

простого

решения,

некоторые пользователи даже прибегают

растровым

ГИС,

жертвуя точностью, чтобы избежать частых утомительных подгонок

изображений.

Как

вы

можете догадаться, данная проблема обостряется, если

мы

пытаемся сравнивать разнородные покрытия. Например, наложение

покрытий почв

растительности вообще

не

позволяет предполагать

совпадение каких-либо двух полигонов. Целью наложения может быть

именно обнаружение расхождений,

и мы

сталкиваемся

необходимостью

отделения реальных различий полигонов

от

ошибок.

К сожалению, несмотря

на

продолжающиеся исследования

по

определению величины погрешности образуемых

результате наложения

покрытий, есть очень мало общих принципов

еще меньше ответов

на

этот

вопрос, особенно если покрытия приходят

из

разных источников

[Chrisman,

1987].

Чаще всего вам придется полагаться

на

собственные опыт

интуицию.

Ваши решения должны основываться

на

вашем собственном знании данных,

их качества, качества

их

ввода

даже

полевой работе, давшей

их.

Ваши

действия в значительной степени зависят

от

того, насколько точны должны

быть результаты

для

решаемой задачи. Логично предположить,

что

если

вы

имеете несколько покрытий,

то

результат наложения будет иметь

погрешность наихудшего

из

них, хотя

на

самом деле

это не

обязательно так,

о чем тоже следует помнить. Если веса покрытий

наложении неодинаковы,

то

вклады ошибок будут разными. Кроме того, значимость покрытий

для

целей анализа может быть различной даже

при

равном

их

участии

самом

процессе наложения. Поэтому, перед выполнением наложения следует

хорошенько изучить данные, чтобы понять, какая величина погрешности

может быть приемлема.

Дасиметрическое картографирование

В завершение темы наложения следует рассмотреть один старый

картографический метод детализации полигональной информации

на

основе других показателей.

Этот метод, называемый дасиметрическим картографированием

(dasymetric

mapping),

основан

на

идее картограмм, рассмотренной

Птаве

3, и

позволяет

понять некоторый подходы,

уже

использующиеся

в ГИС, как и

другие,

которые еще

не

используются.

Он

может применяться

числовым данным,

существующим

виде статистической поверхности. Первое

документированное применение дасиметрического картографирования

относится

улучшению классификации плотности населения

помощью

так называемого очерчивания

зон

плотности

(density zone

outlining)

[McCleary,

1969].

Этот метод, известный также

как

плотность частей,

использовался

для

достижения большей детальности плотностей

не

входящих в выборку

(unresampled)

областей

на

основе более точного знания

некоторых меньших подобластей, которые входили

выборку

(resampled)

[Wright,

1936].

Есть прекрасный пример использования плотности частей

[Robinson

al.,

1995],

тесно связанный

оригинальным методом Райта

1936

года. Этот метод позволяет улучшить качество количественных данных

полигонального покрытия посредством сравнения

более подробными

данными другого покрытия.

Мы

уже

рассматривали один

из

методов дасиметрического

картографирования,

не

обозначая его как такового: настоящая дасиметрия,

впервые примененная Хаммондом

[Hammond,

1964] в его

работе

формах

рельефа, включает очерчивание

или

классификацию областей

геоморфологических типов

на

основе переклассификации топографических

данных. Топографические поверхности прекрасно подходят

для

этого

метода, который требует непрерывных распределений бесконечного числа

точек. Рассматривая переклассификацию непрерывных поверхностей,

мы

создавали окрестности взаимной видимости, южных склонов, крутых

склонов

других посредством группировки выбранных интервалов наших

наборов данных.

Это

была измененная форма дасиметрического

картографирования. Еще

раз мы

можем увидеть,

что

современные методы

имеют корни

докомпьютерных временах.

Могут оказаться полезными несколько других форм дасиметрического

картографирования; среди наиболее мощных

использование других

регионов

предположением корреляции,

со

значительным вовлечением

некоторой формы картографического наложения. Посмотрев

на

пример

плотностью частей, мы могли бы сказать, что это тоже сравнение показателей

между картами,

но

подход

предположением корреляции существенно

отличается. Вместо обособления участков области,

для

которых подробное

исследование улучшает информационное содержание,

использования этой

информации

для

улучшения наших знаний

об

остальном, здесь

мы

используем либо ограничивающие показатели, либо связанные показатели,

содержащиеся в других покрытиях.

Мы использовали вариант дасиметрического картографирования

ограничивающими переменными (limiting

variables) при

обсуждении

исключающих факторов

наложении.

качестве примера применения для

улучшения качества полигональных данных

моделей, создаваемых

на их

основе, допустим, что мы имеем дело

картой численности населения штата

Миннесота

по

округам.

У нас

есть также карта, содержащая

качестве

полигональных атрибутов площади округов. Наложив

два

покрытия

поделив население

на

площадь, мы получим карту плотности населения для

каждого округа штата. Однако, Миннесота

"страна десяти тысяч озер",

что подразумевает наличие значительных площадей,

на

которых люди

не

живут, если только

не в

плавучих домах. Чтобы улучшить результат,

мы

должны

для

каждого округа "исключить"

из

покрытия площадей водную

поверхность. Если бы мы не применили этот "офаничивающий показатель"

для покрытия площадей округов

использовали результат

для

создания

покрытия плотности населения, то плотность населения округов

крупными

водоёмами оказалась

бы

меньше реальной.

Эти методы могут часто использоваться совместно

картографическим

наложением

для

изоляции

отсева областей, вносящих систематические

отклонения

количественные полигональные данные.

Наш последний пример дасиметрического картографирования,

использующий связанные переменные

(related variables),

очень близок

математическому наложению, как растровому, так

векторному. Показатели

полигональных покрытий часто объединяются при помощи операций более

сложных,

чем

простое исключение. Статистические подходы, такие

как

корреляция

регрессия, часто используются

для

демонстрации того,

что

географически рассеянные феномены связаны другсдругом, итого,

как

эти

отношения позволяют

нам

предсказывать вариации одного

зависимости

от изменений другого. Это верно и при использовании ГИС. Например, если

мы знаем,

что

существует сильная корреляция между процентом пахотной

земли

процентом уклона,

то мы

можем предсказать количество пахотной

земли

на

основе этой корреляции. Имея такую информацию,

мы

можем

создать подробное предсказательное покрытие процента пахотной земли

на

основе одного только уклона.

наоборот, имея покрытия существующих

процентов пахотной земли

уклона, через картографическое наложение

мы

могли

бы

создать покрытие, показывающее реальное отношение между

этими двумя показателями

определенной области. Потом

мы

могли

бы

наложить

это

покрытие

на

покрытие предсказываемого процента пашни

визуально обнаружить расхождения, численные значения которого можно

использовать

для

оценки предсказательной модели. Далее области

расхождений могут сравниваться

другими покрытиями

для

выработки

гипотез

причинах расхождения.

Это

прекрасный пример того,

как ГИС

могут использоваться для выработки гипотез

научных применениях ГИС,

или создания предсказательных геоинформационных моделей для принятия

решений в коммерческих приложениях ГИС.

Дасиметрическое картографирование имеет большой потенциал

улучшения использования ГИС как в академической, так и в коммерческой

среде. Но этот вопрос всё ещё недостаточно освещен в литературе по ГИС.

растровых ГИС легко могут выполняться многие формы дасиметрического

картографирования, а некоторые его методы используются каждый день

даже без осведомленности пользователей об этом. Векторные ГИС также

реализуют многие, если не все, подобные методы, но очень не многие

пытались оценить их потенциал серьезным, систематическим образом

[Gerth,

1993].

Осведомленность о дасиметрии как о потенциальном наборе

методов картографического наложения, скорее всего, приведет к

значительному усовершенствованию доступных сегодня пользователям

инструментов наложения в ГИС.

НЕСКОЛЬКО ПОСЛЕДНИХ ЗАМЕЧАНИЙ

НАЛОЖЕНИИ

Вследствие визуальной привлекательности и интуитивной природы

картографического наложения этот набор методов часто считается тем, что

собственно и есть ГИС. Такое понимание ограничивает число

потенциальных пользователей ГИС и может даже привести к снижению

продаж коммерческих продуктов. Вдобавок, это мешает многим

пользователям в их освоении других эффективных методов, уже имеющихся

в ГИС. Вам следует помнить, что, несмотря на силу картографического

наложения, есть множество альтернативных методов решения

геоинформационных задач. Наложение часто оказывается гораздо более

полезным при объединении с другими методами пространственного анализа,

нежели при использовании его в одиночку. В следующей главе мы займемся

комплексными картографическими моделями, которые потребуют выбора

адекватных методов и объединения их рациональным образом для получения

полезных результатов.

Постоянно помните о том, что никакая ГИС не сможет сама решить,

являются ли используемые вами покрытия функционально связанными.

Прежде чем слепо налагать покрытия, выясните, какие пространственные

факторы могут быть связанными и почему. Можно даже сделать выборку и

проверить гипотезу для обоснования вашего решения.

Часто оказывается полезным статистический подход с использованием

интегрированных единиц местности

(integrated

terrain

units

(ITUs))

[Dangermond,

1976].

Во многом подобно фЦзико-биологическим единицам

картографирования, они отражают положение о том, что все данные

интегрированы на земной поверхности, и что используемые методы, такие

как расшифровка аэрофотоснимков, требуют извлечения этих

взаимодействующих показателей из одного источника информации. Это