Deitz J.E., Southam J.L. Contemporary Business Mathematics for Colleges

Подождите немного. Документ загружается.

a table of future value of annuity factors (FVAFs). It is used the same way as Table 16-1.

As in Table 16-1, the columns in Table 23-1 indicate the periodic interest rate and the rows

indicate the number of periods.

464 Part 6 Corporate and Special Applications

to Use Table 23-1 to Compute Future Value and Total

Interest Earned

1. Locate the annuity factor (FVAF) in the correct row and column of Table

23-1, on pages 488–489.

2. Multiply the payment amount by the annuity factor (FVAF).The product

is the future value of the annuity (FVA).

3. Multiply the payment amount by the number of payments.The product

is the total of all payments.

4. Subtract the total of all payments from the future value of the annuity.

The difference is the total interest earned.

STEPS

FUTURE VALUE OF AN ANNUITY FORMULA

If you prefer, Step 2 above may be summarized as a formula, in words or in symbols:

Future value of an annuity 5 Periodic payment 3 Future value of annuity factor

(Table 23-1) or FVA 5 Pmt 3 FVAF

EXAMPLE C

Find the future value of an annuity of four annual payments of $1,000. Each payment is

made at the end of the year, and 10% interest is compounded each year. Also find the to-

tal interest earned over the 4 years.

The annuity factor (FVAF) from Table 23-1 is 4.64100.

Future value of the annuity 5 $1,000 3 4.64100 5 $4,641

Total of the payments 5 4 3 $1,000 5 $4,000

Total interest 5 $4,641 2 $4,000 5 $641

VARIOUS PAYMENT PERIODS

Payments may be made more often than once a year. The only additional requirement

for an ordinary annuity is that the interest be compounded at the same time the pay-

ments are made—semiannually, quarterly, or monthly. We described the method in

Chapter 16, and also use Steps i, ii, and iii in this chapter. However, in this chapter, the

number computed in Step iii represents both the number of payments and the number

of compounding periods.

Just as in Chapter 16, we use Steps i, ii, and iii in Chapter 23 to find

m 5 the number of compounding periods (and payments) in one year

i 5 periodic interest rate 5 annual rate 4 m

n 5 number of periods (payments) in the entire annuity 5

m 3 number of years

These three steps are required whether we use Table 23-1 or a calculator to find the

FVAF.

STEP iii

STEP ii

STEP i

STEP 4

STEP 3

STEP 2

STEP 1

Chapter 23 Annuities 465

EXAMPLE D

Find the future value of an annuity in which $2,600 is deposited at the end of each quarter

for 4 years. Interest is 8% compounded quarterly.

There are m 5 4 compounding periods in 1 year.

Periodic interest rate i 5 8% 4 4 5 2% per period

Number of payments n 5 4 3 4 years 5 16 payments

Use Table 23-1, 2% column and row 16: annuity factor 5 18.63929

Future value 5 $2,600 3 18.63929 5 $48,462.154, or $48,462.15

STEP 2

STEP 1

STEP iii

STEP ii

STEP i

m 5 4

i 550.02

n 5 4 3 4 5 16

0.08

Assume that $5,000 is invested every 6 months for 5 years in an account that pays 6% compounded semiannually.

Compute the future value of the investment. Then compute the total interest earned by the investment.

Semiannual means m 5 2 periods per year.

Periodic rate 5 6% 4 2 5 3% per period

Number of payments 2 3 5 years 5 10 payments

The future value annuity factor from row 10 of the 3.00% column in Table 23-1 is 11.46388.

Future value of the annuity 5 $5,000 3 11.46388 5 $57,319.40

Total of all payments 5 $5,000 3 10 payments 5 $50,000.00

Total interest earned 5 Future value 2 Total payments 5 $57,319.40 2 $50,000.00

5 $7,319.40

✔

CONCEPT CHECK 23.1

USING A CALCULATOR TO COMPUTE ANNUITY

FACTORS (OPTIONAL)

Recall from Chapter 16 on Compound Interest that Tables 16-1 and 16-2 showed the

“future value factors” (FVF) and the “present value factors” (PVF), respectively. Recall

also that you could use a calculator to find the FVF and PVF with these simple formulas:

FVF 5 (1 1 i)

and PVF 5 1 4 (1 1 i)

(or PVF 5 (1 1 i)

), where i is the periodic

interest rate and n is the total number of periods. To find the future value of $5,000

invested at 8% compounded quarterly for 3 years, you used either Table 16-1 or a calculator

to find FVF 5 1.26824. The future value is FV 5 PV 3 FVF 5 $5,000 3 1.26824

5 $6,341.20.

We defined the terms in Table 23-1 as “future value of annuity factors (FVAFs).”

Just as there was a calculator formula for FVF, there is a calculator formula for

FVAF. It is

where i is the periodic interest rate written as a decimal (as in Chapter 16)

n is the total number of payments (or the number of periods).

FVAF 5

(1 1 i)

2 1

m 5 2

i 550.03

n 5 2 3 5 5 10

0.06

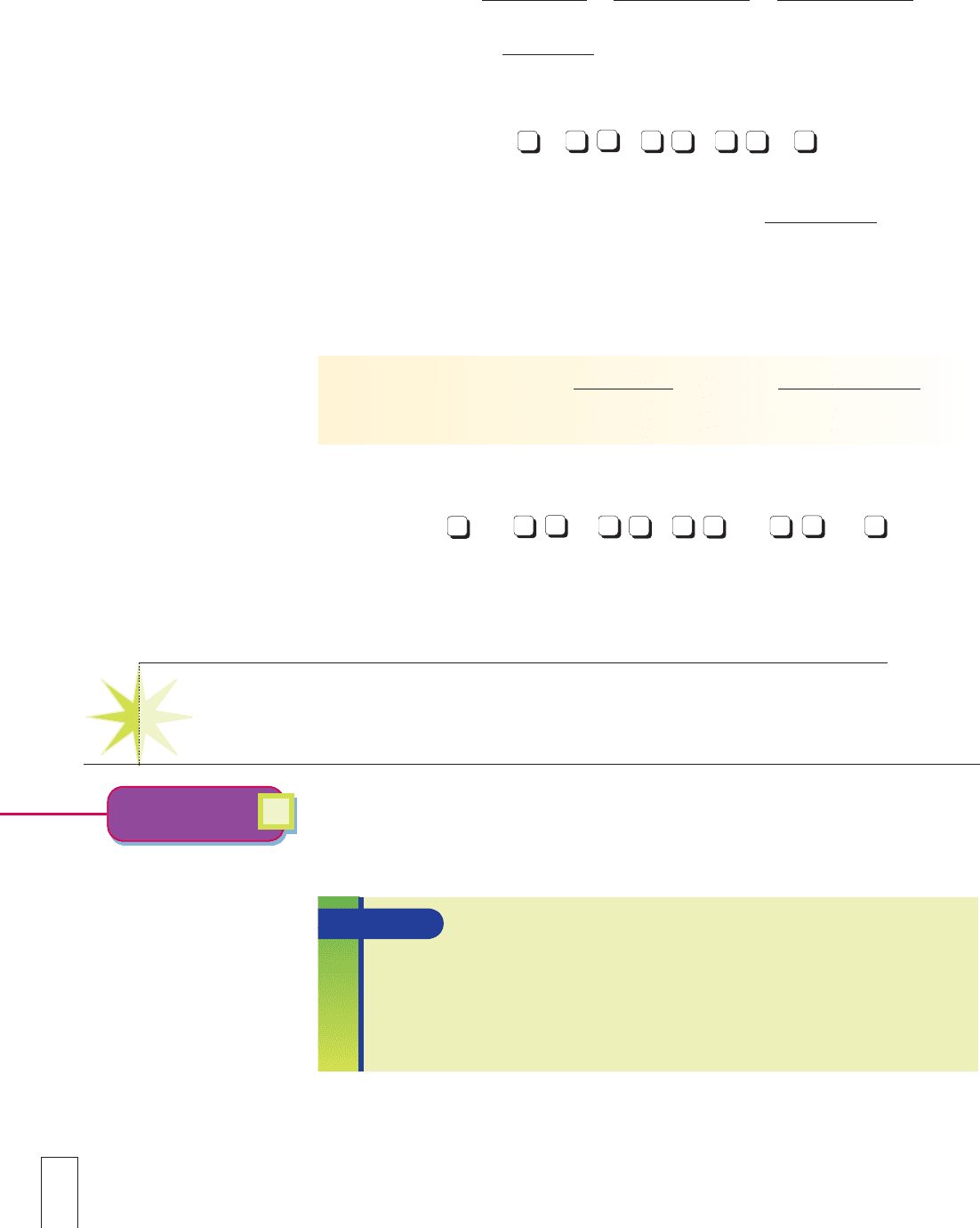
Applying the formula to example C where n 5 4 years and i 5 10% compounded annu-

ally, we find the same FVAF 5 4.46100 as in row 4, column 10%, of Table 23-1:

Depending on your calculator, one set of calculator keystrokes to calculate this FVAF is

1 .1 4 1 .1

To compute the future value of an annuity with a calculator, the formula is

FVA 5 Pmt 3 FVAF or

In example C, FVA 5 Pmt 3 FVAF 5 $1,000 3 4.64100 5 $4,641.

In example D, Steps i, ii, and iii give m 5 4, i 5 6% 4 4 5 1.5% or 0.015, and

n 5 4 3 5 years 5 20. Using the formula and a calculator, we get

After first calculating i 5 0.015 and n 5 20, one typical set of calculator keystrokes to

find the future value is

1 .015 20 1 .015 200

Calculators differ. If your calculator has parentheses, you could use one or more pairs

of parentheses to make an expression that you think is simpler. Use the keystrokes that

seem simplest to you.

5 $200 3 23.1236671 5 $4,624.73

FVA 5 Pmt 3 FVAF 5 Pmt 3 c

(1 1 i)

2 1

d 5 $200 3 c

(1 1 0.015)

2 1

0.015

FVA 5 Pmt 3 c

(1 1 i)

2 1

0.46410000

0.10

5 4.6410000

FVAF 5

(1 1 i)

2 1

(1 1 0.10)

2 1

0.10

1.46410000 2 1

0.10

466 Part 6 Corporate and Special Applications

Learning Objective

Compute the regular payments of an

annuity from the future value.

In examples A–D, the amounts of the payments were known and the future values were

unknown. But when the future value is known, you can compute the amount of each

payment. The procedure is identical whether you use Table 23-1 or a calculator to find

the FVAF.

to Find the Size of the Payment in an Annuity, Given Its

Future Value

1. Determine the annuity factor (FVAF) using Table 23-1 or a calculator.

2. Divide the future value by the annuity factor.The quotient is the amount

of each payment in the annuity.

STEPS

As a formula, Step 2 could be written as Pmt 5 FVA 4 FVAF.

Computing Regular Payments of an Annuity

from the Future Value

Chapter 23 Annuities 467

EXAMPLE E

Nate and Nan Roth want to have $85,000 in their credit union account when their son

Danny starts college. They will make equal payments every month for 4 years. The credit

union will pay 6% compounded monthly. What should their payment amount be?

The value of the annuity at the end, or the future value of the annuity, is $85,000. Use

Table 23-1.

There are m 5 12 compounding periods in 1 year.

Periodic interest rate 5 6% 4 12 5 0.5% per period

Number of deposits 5 12 3 4 years 5 48 deposits

Use Table 23-1, 0.5% column and row 48: annuity factor 5 54.09783

Future value of the annuity 5 $85,000

Payment amount 5 $85,000 4 54.09783 5 $1,571.2275, or $1,571.23

SINKING FUNDS

At the beginning of this chapter, we mentioned that a $10,000,000 corporate bond issue

may include a sinking fund feature. Sometimes a sinking fund means that the corporation

will set aside an equal amount of money each year so that by the end of the 20 years, the

corporation will have accumulated the $10,000,000. At other times, perhaps, a sinking fund

may be used by the corporation to buy back $500,000 worth of the bonds each year.

Although the term sinking fund may be most often associated with the repayment of

a bond issue, its use isn’t restricted to bonds. A corporation may set up a sinking fund to

save money for an expensive piece of equipment that it knows it must replace in the

future. The college fund set up by Nate and Nan Roth in example E was essentially a

sinking fund.

EXAMPLE F

Micromedia Corporation is preparing a $20,000,000 bond issue. The company wants

to make 25 equal annual payments into a sinking fund so that it will have a total of

$20,000,000 available in 25 years to repay the bonds. What size should each of the

payments be if the company can earn 6% per year on the payments?

There is m 5 1 compounding period in 1 year.

Periodic interest rate 5 6% 4 1 5 6% per period

Number of deposits 5 1 3 25 years 5 25 deposits

Use Table 23-1, 6% column and row 25: annuity factor 5 54.86451

Future value of the annuity 5 $20,000,000

Payment amount 5 $20,000,000 4 54.86451 5 $364,534.38

STEP 2

STEP 1

STEP iii

STEP ii

STEP i

STEP 2

STEP 1

STEP iii

STEP ii

STEP i

m 5 12

i 550.005

n 5 12 3 4 5 48

FVAF 5

5 54.09783222

(1 1 0.005)

2 1

0.005

0.06

m 5 1

i 550.06

n 5 1 3 25 5 25

FVAF 5

5 54.86451100

(1 1 0.06)

2 1

0.06

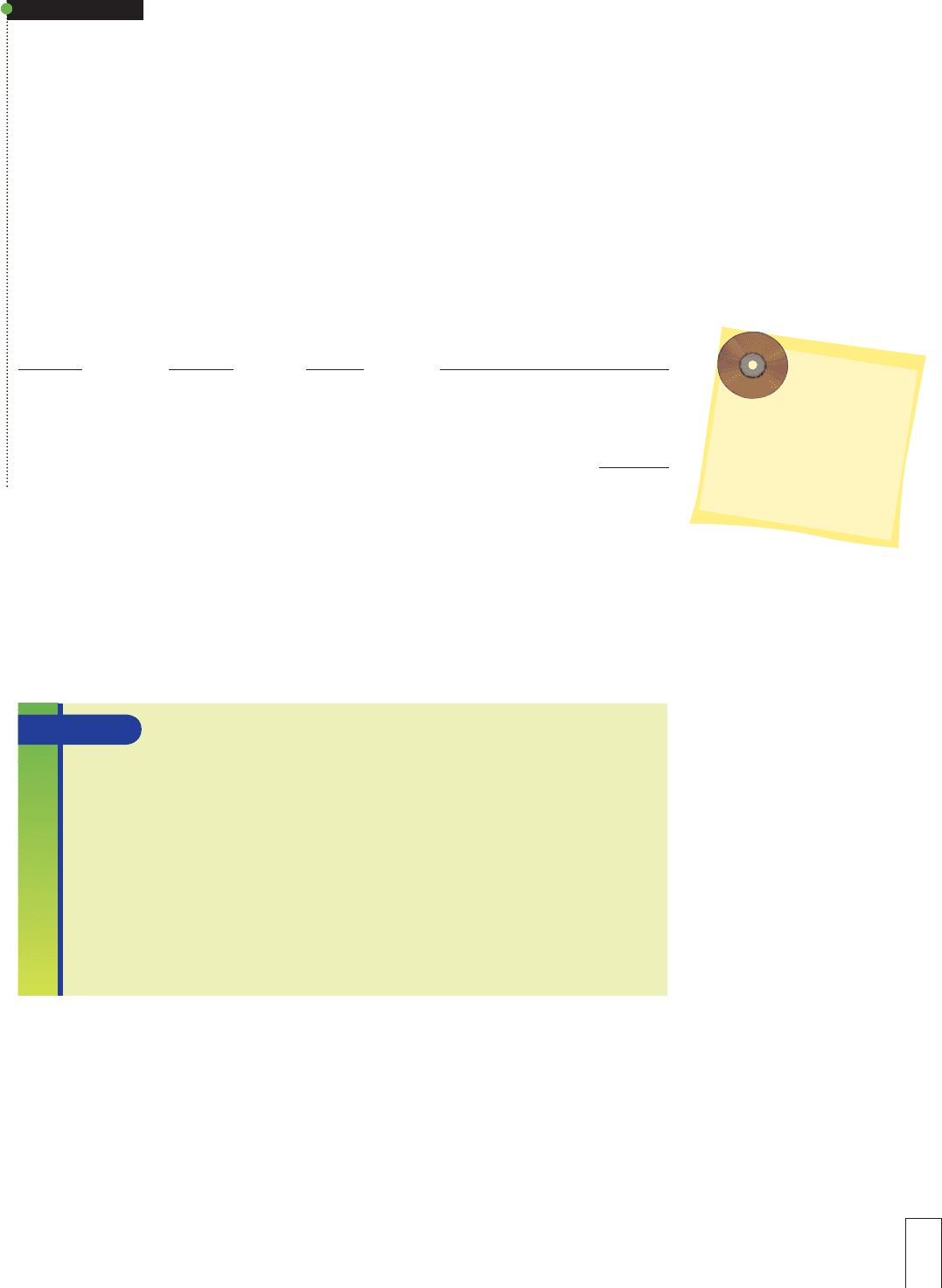
The annuity shown in Figure 23-3 begins December 31, 2009. Again, the value of the

annuity on this date is called the present value of the annuity. For example, when a person

deposits a large amount in a bank account and then makes a series of equal withdrawals

from the account until it is empty, the series of withdrawals (the equal payments) is the

annuity, and the amount deposited is the present value. The interest earned equals the

difference between the total amount withdrawn and the amount deposited.

468 Part 6 Corporate and Special Applications

Assume that an equal amount is invested every quarter for 7 years. After the last payment,the future value is

$75,000. If the interest rate is 8% compounded quarterly, compute the size of each regular quarterly payment.

Quarterly means m 5 4 periods per year.

Periodic rate 5 8% 4 4 5 2% per period

Number of payments is 4 3 7 years 5 28 payments

The future value annuity factor from row 28 of the 2% column in Table 23-1 is

37.05121.

Regular quarterly payment 5 $75,000 4 37.05121 5 $2,024.2254, or $2,024.23

COMPLETE ASSIGNMENT 23.1.

✔

CONCEPT CHECK 23.2

m 5 4

i 550.02

n 5 4 3 7 5 28

FVAF 5

5 37.05121031

(1 1 0.02)

2 1

0.02

0.08

Computing the Present Value of an Annuity

Learning Objective

Compute the present value of an

annuity.

Figure 23-3 Present Value of an Ordinary Annuity

12/31/13

$1,000

12/31/09

$ 909.09

826.45

751.31

+ 683.01

$3,169.86

Date

Period

Payment

Present

1234

12/31/10

$1,000

12/31/11

$1,000

12/31/12

$1,000

= Present value of the annuity = Total value on 12/31/09

Chapter 23 Annuities 469

EXAMPLE G

In November 2009, Ashley Hamilton inherited some money. She planned to donate

part of the money immediately to the American Cancer Society and then to make four

equal donations of $1,000 each on December 31 of 2010, 2011, 2012, and 2013. To

prepare for the four future payments, Ashley went to her bank on December 31, 2009,

and deposited money into a new account. The account paid 10% compounded annually.

Ashley would withdraw $1,000 each year always on December 31. After the last withdrawal

on December 31, 2013, the account would be empty.

How much must Ashley deposit on December 31, 2009? (Hint: Make a time line dia-

gram, and compute the present value of each of the four withdrawals.)

To find the present value of the annuity on December 31, 2009, first use Table 16-2 to

find the present value of each of the four payments on December 31, 2009. Then com-

pute the total.

Amount of Date of Years of Present Value

Payment Payment Interest on 12/31/09

$1,000 12/31/10 1 $1,000 3 0.90909 5 $ 909.09

$1,000 12/31/11 2 $1,000 3 0.82645 5 826.45

$1,000 12/31/12 3 $1,000 3 0.75131 5 751.31

$1,000 12/31/13 4 $1,000 3 0.68301 51 683.01

Present value of the annuity on 12/31/09 5 $3,169.86

Figure 23-3 illustrates example G. The time line shows the equal withdrawals as each

payment is moved from the future backward to the present (to December 31, 2009).

Compare Figure 23-3 with Figure 23-2 where each payment was projected forward into

the future.

The method shown in Figure 23-3 aids instruction but is too time-consuming to be

practical. To get the same solution quickly, use Table 23-2 on pages 490–491.

23.7 Instructors,point out that,for

income tax planning purposes,tax-

payers may make charitable contribu-

tions on the last day of the year.In

some years,December 31 is a Sunday,

so a withdrawal for a cash contribution

would have to be on December 29 or

30.However you still might write the

check on December 31.

to Use Table 23-2 to Compute Present Value and Total

Interest Earned

1. Locate the present value of annuity factor (PVAF) in the correct row

and column of Table 23-2 on pages 490–491.

2. Multiply the payment amount by the annuity factor (PVAF).The product

is the present value of the annuity.

3. Multiply the payment amount by the number of payments.The product

is the total of all payments.

4. Subtract the present value of the annuity from the total of all payments.

The difference is the total interest earned.

STEPS

PRESENT VALUE OF AN ANNUITY FORMULA

If you prefer, Step 2 may be summarized as a formula, in words or in symbols:

Present value of an annuity 5 Periodic payment 3 Present value of annuity factor

(Table 23-2), or PVA 5 Pmt 3 PVAF.

Annuities:

Future Value/

Present Value

Video

For example G, the factor in the 10.00% column and row 4 of Table 23-2 is 3.16987

(Step 1), and $1,000 3 3.16987 5 $3,169.87 (Step 2).

The application in example H may not sound complicated, but it would be tedious to

compute without Table 23-2. Because the payments and compounding are quarterly, use

Steps i, ii, and iii to find the periodic rate and the number of periods.

EXAMPLE H

Nanda Cerrado just won first prize in a fund-raising raffle. Nanda has a choice: She can re-

ceive quarterly payments of $750 each for 6 years, with the first payment 3 months (one

quarter) from now, or she can receive 1 lump sum today. Assuming an interest rate of 6%

compounded quarterly, what lump sum today equals the future payments? (Hint: The se-

ries of $750 payments is an annuity, and the lump sum is the present value of the annuity.)

There are m 5 4 compounding periods in 1 year.

Periodic interest rate 5 6% 4 4 5 1.5% per period

Number of payments 4 3 6 years 5 24

Using Table 23-2, 1.50% column and row 24: the PVAF 5 20.03041

Present value 5 $750 3 20.03041 5 $15,022.8075, or $15,022.81

STEP 2

STEP 1

STEP iii

STEP ii

STEP i

470 Part 6 Corporate and Special Applications

m 5 4

i 550.015

n 5 4 3 6 5 24

0.06

What present value (principal) must be invested today in an account to provide for 7 equal annual withdrawals

(an annuity) of $5,000 each? The interest rate is 8% compounded annually.

✔

CONCEPT CHECK 23.3

m 5 1

i 550.08

n 5 1 3 7 5 7

0.08

USING A CALCULATOR TO COMPUTE THE PRESENT

VALUE OF AN ANNUITY (OPTIONAL)

Just as there is a calculator formula to compute the future value of an annuity factor

(FVAF), there is also a calculator formula to compute the present value of an annuity

factor (PVAF). The formula can be written several ways. Use whichever one you think is

easier to understand.

or PVAF 5

1 2

(1 1 i)

PVAF 5

1 2 (1 4 (1 1 i)

)

PVAF 5

1 2 (1 1 i)

2 n

Annual means m 5 1 period per year.

Periodic rate 5 8% 4 1 5 8% per year

Number of payments 5 1 3 7 years 5 7 payments

From row 7 of the 8.00% column of Table 23-2, the PVAF 5 5.20637.

Present value of the annuity 5 $5,000 3 5.20637 5 $26,031.85

Chapter 23 Annuities 471

where i is the periodic interest rate written as a decimal (as in Chapter 16)

n is the number of payments (or the number of periods)

To compute the present value of an annuity (PVA) with a calculator, the formula is

PVA 5 Pmt 3 PVAF or

where Pmt is the periodic payment

i is the periodic interest rate written as a decimal

n is the number of payments (or the number of periods)

PVA is the present value of the annuity

Return to example H and use the formulas for PVA and PVAF to compute the present

value of the annuity in example H: Quarterly payments of $750 each for 6 years at an

interest rate of 6% compounded quarterly.

Pmt 5 $750

m 5 4 compounding periods in 1 year

i 5 6% 4 4 5 1.5%, or 0.015, is the periodic interest rate

n 5 4 3 6 years 5 24 is the number of compounding periods

55$15,022.80402, or $15,022.80

After first calculating i 5 0.015 and n 5 24, one typical set of calculator keystrokes to

find the present value is 1 .015 24 1 .015

750

And remember: Your calculator may be different. You may have to use different

keystrokes and you may be able to find a more efficient sequence of keystrokes.

1/2

$750 3 (20.03040537)

$750 3 c

0.30045608

0.015

d$750 3 c

1 2 0.69954392

0.015

5 $750 3 c

1 2 (1 1 0.015)

2 24

0.015

dPVA 5 Pmt 3 c

1 2 (1 1 i)

2 n

PVA 5 Pmt 3 c

1 2 (1 1 i)

2 n

23.8 Remind students to use the

[1/2] key on their calculators to

make the negative exponent,not

the [2] key.

In examples G and H, the amounts of the payments were known and the present values

were unknown. If, however, the present value is known, then you can compute the

amount of the payments. The procedure is identical whether you use Table 23-2 or a

calculator to find the PVAF.

Compute the regular payments of an

annuity from the present value.

Learning Objective

Computing Regular Payments of an Annuity

from the Present Value

to Find the Size of the Payment in an Annuity, Given the

Present Value

1. Determine the annuity factor (PVAF) using Table 23-2 or a calculator.

2. Divide the present value by the annuity factor (PVAF).The quotient is the

amount of the payments in the annuity.

STEPS

EXAMPLE I

Jim Schremp received a $25,000 bonus from his employer. Rather than spend it all at

once, he decided to deposit it in a bank account that pays 9% compounded monthly. He

will make equal monthly withdrawals for 4 years. After the last withdrawal, the account

will be empty. How much will he withdraw each month?

The value of the annuity in the beginning (present value of the annuity) is $25,000.

Use Table 23-2.

There are m 5 12 compounding periods in 1 year

Periodic interest rate 5 9% 4 12 5 0.75% per period

Number of withdrawals 5 12 3 4 years 5 48 withdrawals

Using Table 23-2, 0.75% column and row 48: the PVAF 5 40.18478

Each withdrawal 5 $25,000 4 40.18478 5 $622.126, or $622.13

STEP 2

STEP 1

STEP iii

STEP ii

STEP i

472 Part 6 Corporate and Special Applications

m 5 12

i 550.0075

n 5 12 3 4 5 48

PVAF 5

5 40.18478189

1 2 (1 1 0.0075)

2 48

0.0075

0.09

Assume that $75,000 is deposited today (the present value) to provide for 36 equal quarterly withdrawals (an annuity)

over the next 9 years. If the interest rate is 6% compounded quarterly, what is the size of each regular quarterly

payment (a withdraw)? What is the total interest earned during the term of the annuity?

Quarterly means m 5 4 periods per year.

Periodic rate 5 6% 4 4 5 1.5% per quarter

Number of payments 5 4 3 9 years 5 36 payments

From row 36 of the 1.50% column in Table 23-2, the PVAF 5 27.66068

Regular quarterly payment 5 $75,000 4 27.66068 5 $2,711.43

Total of all payments 5 $2,711.43 3 36 payments 5 $97,611.48

Total interest earned 5 Total payments 2 Present value

5 $97,611.48 2 $75,000.00 5 $22,611.48

✔

CONCEPT CHECK 23.4

m 5 4

i 550.015

n 5 4 3 9 5 36

PVAF 5

5 27.66068431

1 2 (1 1 0.015)

2 36

0.015

0.06

Chapter 23 Annuities 473

Recall from your study of loan amortization in Chapter 14 that the borrower repays the

loan by making equal monthly payments and that the interest is computed on the un-

paid balance each month. Loan amortization creates an annuity because there is a series

of equal periodic payments. Computing the interest each month makes it compound in-

terest. The amount of the loan is the present value of the annuity.

Stated another way, in amortization, when the amount of the loan is known, the pre-

sent value of the annuity is known. As illustrated in example J, you can use Table 23-2 to

compute the amount of the monthly payments.

Computing the Payment to Amortize a Loan

Compute the loan payment required

to amortize a loan.

Learning Objective

to Find the Size of the Payment to Amortize a Loan

1. Determine the annuity factor (PVAF) using Table 23-2 or a calculator.

2. Divide the loan amount by the annuity factor (PVAF). The quotient is the

amount of the monthly loan payments.

STEPS

EXAMPLE J

Barbara Luzardi buys a new piano. Barbara pays $2,200 cash and also trades in her old

piano. The balance is $4,100 and the piano dealer will amortize the $4,100 over 9 months

at 15%. Find the size of her required monthly payments.

There are 12 compounding periods in 1 year

Periodic interest rate 5 15% 4 12 5 1.25% per period

Number of monthly payments 5 9

Because the borrowing occurs at the beginning of the annuity, this is a

present value problem and $4,100 is the present value of the annuity; use

Table 23-2. In the 1.25% column and row 9, the PVAF 5 8.46234.

Size of each payment 5 $4,100 4 8.46234 5 $484.4996, or $484.50

STEP 2

STEP 1

STEP iii

STEP ii

STEP i

m 5 12

i 550.0125

n 5 9

PVAF 5

5 8.46234498

1 2 (1 1 0.0125)

2 9

0.0125

0.15

A bank loans $40,000 at an interest rate of 9% compounded monthly. Find the loan payment necessary to amortize

the loan with monthly payments over 3 years.

✔

CONCEPT CHECK 23.5

m 5 12

i 550.0075

n 5 12 3 3 5 36

PVAF 5

5 31.44680525

1 2 (1 1 0.0075)

2 36

0.0075

0.09

Loan amortization involves an annuity. The amount borrowed is the present

value of the annuity, and the monthly loan payment is the regular annuity

payment.

Monthly means 12 periods per year.

Periodic rate 5 9% 4 12 5 0.75% per period

Number of payments 5 12 3 3 years 5 36 payments

From row 36 of the 0.75% column of Table 23-2, the PVAF 5 31.44681.

Loan payment 5 $40,000 4 31.44681 5 $1,271.98911, or $1,271.99