Deitz J.E., Southam J.L. Contemporary Business Mathematics for Colleges

Подождите немного. Документ загружается.

454 Part 6 Corporate and Special Applications

Tr3. Complete the following Excel worksheet by entering formulas in the shaded cells

to calculate the Yield to Maturity for six InTT 8.2s18 bonds purchased at a pre-

mium price of 120. The bonds will mature in 12 years.

Hint: Use parentheses to do addition or subtraction before multiplication or

division. Yield to maturity should be shown as a percent.

Market Value of Bonds

Annual Interest

Annual Premium Amortization

Average Principal Invested

Yield to Maturity

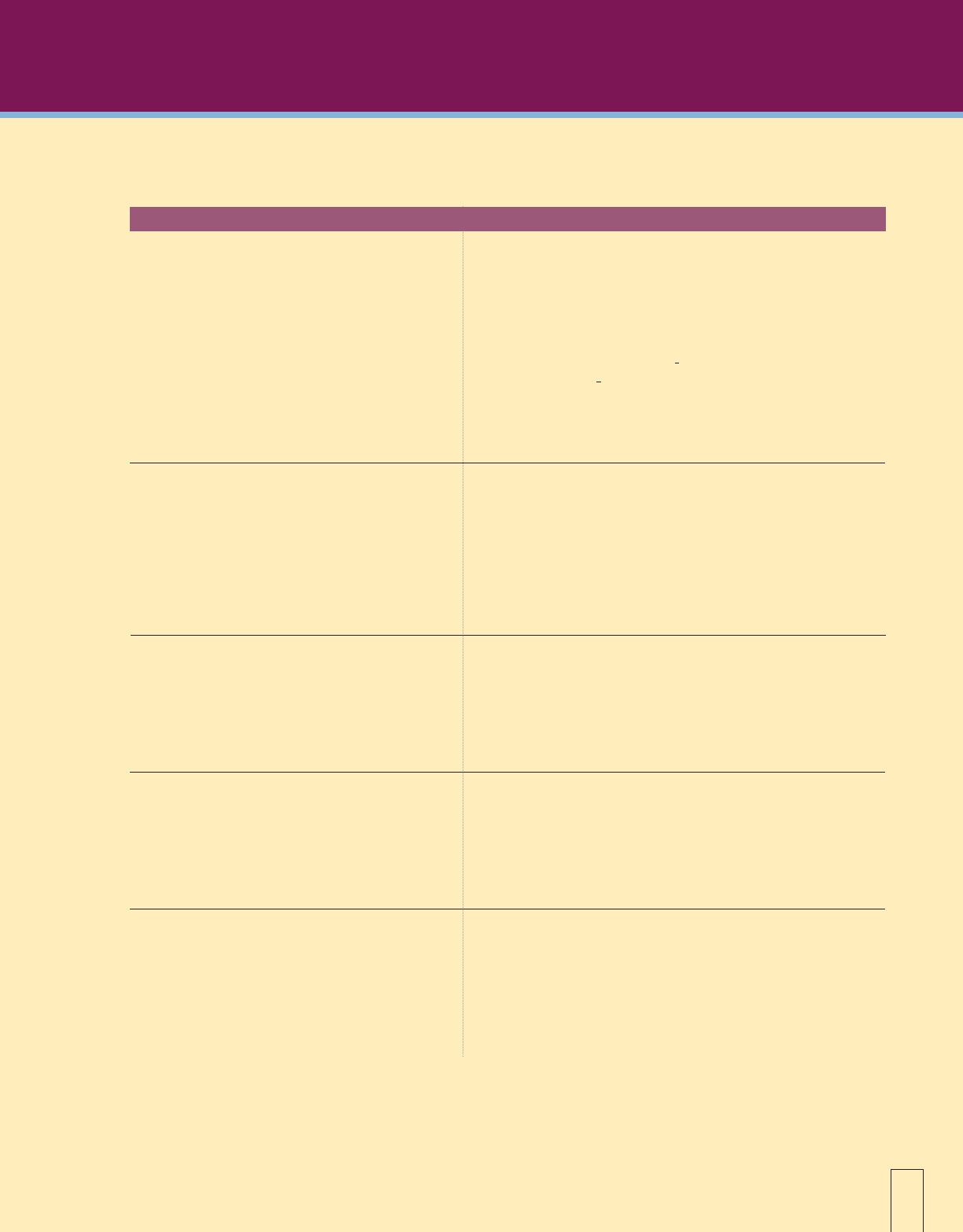
THE BOTTOM LINE

Summary of chapter learning objectives:

Learning Objective

22.1

Compute gains and losses on convertible and callable

corporate bond transactions.

Example

1. John Jacobs bought five DVC bonds at $1,000 per bond. Each bond

was convertible after 3 years to 50 shares of stock. At the end of

3 years, shares of DVC stock were selling at $32. The bond price had

risen to 120. Should Mark exercise his option to convert?

2. Colton Mfg. Corp. issued $2,000,000 worth of callable bonds paying

9% interest. The maturity date for the bonds was in 20 years. Four

years later, interest rates fell to %. The bonds were called, and new

bonds sold at the % rate. How much did Colton Mfg. Corp. save

by calling the bonds?

Answers: 1. The stock has $2,000 greater value; yes, he should convert 2. $480,000 3. Boeing; $350 4. $10.50

5. 8.04% 6. 5.97%

22.2

Compute annual interest on bonds.

3. Amy Coles purchased three 12-year, $1,000 bonds: one Boeing at

7%, one U.S. Treasury at 4.5%, and one Water World Sports at 12%.

If the Water World Sports bond defaulted after 5 years and paid

holders 60%, which bond produced the most income in the 5-year

period, assuming that the $400 loss on the WWS bond was

considered to be a reduction in income? How much did it produce?

22.3

Compute accrued interest on bond transactions made

between interest payment dates.

4. One BLM 9s18 bond was purchased at 102 on February 12. What

was the amount of accrued interest if interest is paid January 1 and

July 1?

22.4

Compute annual yield on bonds selling at a premium or

a discount.

5. Six Khol 7.4s25 bonds were purchased at 92. What was the current

yield?

22.5

Compute a rate of yield to maturity.

6. Three NYR 8s20 bonds were purchased at 120. The bonds will

mature in 14 years. What is the rate of yield to maturity?

Chapter 22 Corporate and Government Bonds 455

456 Part 6 Corporate and Special Applications

SELF-CHECK

Review Problems for Chapter 22

1 Alfred Tennyson purchased 15 IBM 7

⁄

2s18 bonds at 104.

a. What was the cost of the bonds?

b. How often will interest be paid?

c. How much interest will Alfred receive each interest period?

d. Assuming the bonds pay interest on April 1 and October 1, calculate the accrued interest if

the bonds were purchased June 6.

e. What is the total amount Alfred paid for the bonds including accrued interest?

f. Were the bonds purchased at a premium or a discount?

g. What was the amount of the premium or discount?

h. When do the bonds mature?

i. What is the current yield on the bonds?

j. Assume the bonds mature in 12 years. Calculate the yield to maturity.

2 Marta Samuals purchased six Xerox $1,000 convertible bonds at 95. Each bond was convertible into

30 shares of common stock. After 5 years, when the stock was selling at $42, Marta converted all six bonds.

a. How many shares of stock did she receive?

b. What was the value of the stock upon conversion?

c. What was Marta’s gain upon conversion of the bonds?

d. Should Marta convert her bonds into stock if the stock’s current market price is $35 per

share? Why or why not?

3 Avis, Inc., issued $50,000,000 of 9

⁄

2%, 20-year, callable bonds. After 6 years, the interest rate fell to 8%.

How much interest would Avis save by calling the bonds and reissuing bonds at the lower rate?

4 Ron Nelson is considering purchasing one of the following bonds:

MCD 7s15 at a market price of 90

AOC 8s15 at a market price of 100

JBC 9s15 at a market price of 110

Calculate the annual yield and yield to maturity for each bond assuming there are 10 years to maturity for

each bond. Which bond would you recommend Ron purchase based on your computations?

Answers to the Self-Check can be found in Appendix B at the back of the text.

Chapter 22 Corporate and Government Bonds 457

Assignment 22.1: Corporate and Government Bonds

Name

Date Score

A (38 points) Solve the following problems. (points for correct answers as marked)

1. Jean Francis purchased seven IBM $1,000 convertible bonds at $1.05. Each bond was convertible to 25

shares of IBM stock in 5 years. At the end of 5 years, IBM stock was selling at $97. If Jean converted, what

would be her 5-year capital gain? (4 points)

2. Return to problem 1 and assume that the stock price after 5 years was $38. How much more money would

Jean get by cashing in the bonds rather than converting to stock? (4 points)

3. The city of Jamestown, Virginia, issued $27,000,000 worth of callable bonds at 9% on January 1, 2008.

The bonds were due in 2023. If interest rates were to fall to 6.5% on January 1, 2015, how much could

Jamestown save by reissuing the bonds at the 6.5% rate on January 1, 2015? (4 points)

4. Assume that an investor had purchased $500,000 worth of the Jamestown bonds referred to in problem 3.

How much interest would he lose from having the bonds called if he reinvested in the new bond issue?

(4 points)

5. Devi Sharma purchased 22 corporate bonds, as shown. What was her total cost, and how much interest

income would she realize annually? (1 point for each correct answer)

Number

Bond Purchased Price Total Cost Annual Interest

a. Apex s09 4 100

b. DukeP s02 3 98

c. PGE s12 9 86

d. IBM s08 6 109

Total 22

$2,010.00$21,220.00

1 562.501 6,540.00

911.257,740.00

236.252,940.00

$ 300.00$ 4,000.00

$100,000

$5,400,000

$350

$9,625

Learning Objectives

2 3

7 3 $1,000 3 1.05 5 $7,350 purchase price

175 3 $97 5 $16,975 stock value on conversion

$16,975 2 $7,350 5 $9,625 capital gain

7 3 $1,000 5 $7,000 cash from bonds

175 3 $38 5 $6,650 stock value on conversion date

$7,000 2 $6,650 5 $350 more money from cashing in bonds

$27,000,000 3 0.09 5 $2,430,000 annual interest at 9%

$27,000,000 3 0.065 5 $1,755,000 annual interest at 6.5%

$2,430,000 2 $1,755,000 5 $675,000 annual savings

$675,000 3 8 years 5 $5,400,000 savings

$500,000 3 0.09 5 $45,000 annual interest at 9%

$500,000 3 0.065 5 $32,500 annual interest at 6.5%

($45,000 2 $32,500) 3 8 years 5 $100,000

or $500,000 3 0.025 3 8 5 $100,000

a. 4 3 $1,000.00 5 $ 4,000.00 cost $4,000 3 0.075 5 $ 300.00

b. 3 3 $ 980.00 5 $ 2,940.00 cost $3,000 3 0.07875 5 $ 236.25

c. 9 3 $ 860.00 5 $ 7,740.00 cost $9,000 3 0.10125 5 $ 911.25

d. 6 3 $1,090.00 51

6,540.00

cost $6,000 3 0.09375 51

562.50

$21,220.00 $2,010.00

6. What is the dollar amount of interest per year and the maturity date for each of the following $1,000

bonds? (1 point for each correct answer)

Bond Interest Maturity Date Bond Interest Maturity Date

a. PGE 6s08 d. Fldcst s12

b. Avnet 8s13 e. OwCor 12s10

c. CPoWV 9s15 f. Cisco s09

2009$75

2015$90

2010$1202013$80

2012$125

2008$60

458 Part 6 Corporate and Special Applications

Assignment 22.1 Continued

a. $1,000 3 0.065 $60 d. $1,000 3 0.125 5 $125

b. $1,000 3 0.08 5 $80 e. $1,000 3 0.12 5 $120

c. $1,000 3 0.09 5 $90 f. $1,000 3 0.075 5 $75

Score for A (38)

B (50 points) Solve the following problems. (points for correct answers as marked)

7. In each of the following problems, determine the number of days for which accrued interest is paid and

the total purchase payment made for the bonds. (5 points for each correct answer)

a. On September 12, Tracy Dean bought, at 103 plus accrued interest, two IBM 9s10 bonds with interest paid on

January 1 and July 1.

Number of days accrued interest: Total payment:

b. On October 9, Ben Blue bought, at 93 plus accrued interest, three IBM s09 bonds with interest paid on

January 1 and July 1.

Number of days accrued interest: Total payment:

$2,852.50100

$2,096.5073

a. Purchase date: September 12 b. Purchase date: October 9

(July) 31 1 (Aug.) 31 1 (Sept.) 11 5 73 days (July) 31 1 (Aug.) 31 1 (Sept.) 30 1 (Oct.) 8 5 100 days

$2,000 3 1.03 5 $2,060 market value $3,000 3 0.93 5 $2,790 market value

$2,000 3 0.09 35$36.50 accrued interest $3,000 3 0.075 35$62.50 accrued interest

$2,060 1 $36.50 5 $2,096.50 total purchase payment $2,790 1 $62.50 5 $2,852.50 total purchase payment

100

360

8. Jack Mueller purchased a $1,000 corporate bond with a rating of AAA, paying 8% per year. Tom

Bronkowski purchased a $1,000 junk bond paying 20%. Each bond was to mature in 10 years. Jack’s bond

paid interest for the 10-year period and face value at maturity. Tom’s junk bond paid interest for 3 years

before the company filed for bankruptcy and paid 45 cents on the dollar to its bondholders. How much

more did Jack receive from his investment than Tom received from his? (10 points)

Jack: $1,000 3 0.08 3 10 years 5 $800 interest; $800 1 $1,000 face value 5 $1,800 received

Tom: $1,000 3 0.20 3 3 years 5 $600 interest; $600 1 $450 5 $1,050 received

$1,800 2 $1,050 5 $750 more

9. Compute the current yield for the following bonds. (5 points for each correct answer)

Bond Price Current Yield

a. PepsiCo 9s08 108

b. IBM 93.5

c. Avitar 10s12 112

d. ABM 6s08 82

7.32%

8.93%

7.89%

s08

8.33%

a. ($1,000 3 0.09) 4 $1,080 5 0.08 , or 8.33% or a. 9 4 108 5 0.0833, or 8.33%

b. ($1,000 3 0.07375) 4 $935 5 0.078877, or 7.89% or b. 7.375 4 93.5 5 7.89%

c. ($1,000 3 0.10) 4 $1,120 5 0.08929, or 8.93% or c. 10 4 112 5 8.93%

d. ($1,000 3 0.06) 4 $820.00 5 0.07317, or 7.32% or d. 6 4 0.82 5 7.32%

Score for B (50)

Chapter 22 Corporate and Government Bonds 459

Assignment 22.2: Bond Rate of Yield

Name

Date Score

A (52 points) Solve the following problems. (points for correct answers as marked)

1. An investor bought a 7.4% bond at 90. The bond would mature in 8 years. Round answers to two decimal

places. (4 points for each correct answer)

a. What was the average annual yield? b. What was the rate of yield to maturity?

9.11%8.22%

Learning Objectives

$1,000 3 0.9 5 $900 purchase price ($1,000 2 $900) 4 8 5 $12.50 annual discount

$1,000 3 0.074 5 $74 annual interest

average principal invested

$74 4 $900 5 8.22%

or 7.4 4 0.90 5 8.22% ($74 1 $12.50) 4 $950 5 9.11%

$1,000 1 $900

5 $950

2. In 2008, Jim Ayers bought six LTV 5s23 bonds for which he paid 82. Three years later, he sold the bonds at

84 and bought six Southern Electric s30 bonds at 93. Did he increase or decrease the original rate of

yield to maturity, and, if so, by how much? Round yields to one decimal place. (14 points)

3.4% increase

LTV Southern Electric

2023 2 2008 5 15 years to run 2030 2 2011 5 20 years to run

$6,000 3 0.05 5 $300 annual interest $6,000 3 0.095 5 $570 annual interest

$6,000 3 0.82 5 $4,920 market value $6,000 3 0.93 5 $5,580 market value

($6,000 2 $4,920) 4 15 years 5 $72 annual discount ($6,000 2 $5,580) 4 20 years 5 $21 annual discount

amortization amortization

average principal invested average principal invested

($300 1 $72) 4 $5,460 5 0.0681 5 6.8% yield to ($570 1 $21) 4 $5,790 5 0.1021 5 10.2% yield to

maturity maturity

10.2% 2 6.8% 5 3.4% increase

$6,000 1 $5,580

5 $5,790

$6,000 1 $4,920

5 $5,460

$4,000 3 0.085 35$141.67 interest 9.66%

$3,520 1 $141.67 5 $3,661.67 $4,000 3 0.085 5 $340 interest

$340 4 $3,520 5 9.66%, or 8.5 4 0.88 5 9.66%

150

360

EM&E Standard of California

For one bond: $1,000 3 1.065 5 $1,065 market value For one bond: $1,000 3 0.8 5 $800 market value

$1,000 3 0.085 5 $85 annual interest per bond $1,000 3 0.06 5 $60 annual interest paid per bond

($1,065 2 $1,000) 4 13 years 5 $5 annual premium ($1,000 2 $800) 4 10 years 5 $20 annual discount

amortization per bond amortization per bond

average principal invested average principal invested

($85 2 $5) 4 $1,032.50 5 0.0775 5 7.7% yield to ($60 1 $20) 4 $900 5 0.0889 5 8.89% yield to

maturity maturity

$1,000 1 $800

5 $900

$1,000 1 $1,065

5 $1,032.50

3. On July 29, Ann McCoy purchased four GMC 8 s09 bonds at 88. Interest was payable March 1 and

September 1. Included in Ann’s cost was accrued interest for 150 days. (4 points for each correct answer)

a. What was the total purchase cost? b. What was the average annual yield? Do not consider

accrued interest when calculating this rate of yield.

$4,000 3 0.88 5 $3,520 market value

$3,661.67

4. In 2008, Benito Cooper planned to purchase 20 $1,000 bonds and hold them to maturity. He had two

choices: The first was EM&E s21 at 106.50. The second was Standard of California 6s18 at 80. Benito

purchased the issue that provided the higher rate of yield to maturity.

a. Which issue did Benito purchase? (12 points)

Standard of California

b. How much income would Benito have earned monthly if Standard of California had been purchased? (3 points)

$133.33

460 Part 6 Corporate and Special Applications

Assignment 22.2 Continued

$20,000 face value 3 0.06 5 $1,200 annual yield 4 12 5 $100 monthly

$1,000 2 $800 5 $200 3 20 5 $4,000 4 10 5 $400 annually 4 12 5 $33.33 monthly amortization

$100 1 $33.33 5 $133.33 monthly

a. $8,000 3 0.08 5 $640 annual interest

$400 4 5 5 $80 premium amortization

$8,000 3 1.05 5 $8,400 market value

($8,400 1 $8,000) 4 2 5 $8,200 average principal

($640 2 80) 4 $8,200 5 0.6829, or 6.83% yield

b. $10,000 3 0.06 5 $600 annual interest

$300 4 10 5 $30 discount amortization

$10,000 3 0.97 5 $9,700 market value

($9,700 1 $10,000) 4 2 5 $9,850 average principal

($600 1 $30) 4 $9,850 5 0.063959, or 6.40%

c. $12,000 3 0.075 5 $900 annual interest

$1,680 4 8 5 $210 discount amortization

$12,000 3 0.86 5 $10,320 market price

($10,320 1 $12,000) 4 2 5 $11,160 average principal

($900 1$210) 4 $11,160 5 0.099462 5 9.95%

8.9% yield to maturity for EM&E

8.9% yield to maturity for Standard of California; 0.0889 is slightly better than 0.0886

$1,000 3 0.975 5 $975 market value

$1,000 3 0.085 5 $85 annual interest per bond

($1,000 2 $975) 4 10 years 5 $2.50 annual discount amortization per bond

5 $987.50 average principal invested

($85 1 $2.50) 4 $987.50 5 0.886 5 8.9% yield to maturity

$1,000 1 $975

c. If, in 2011, Benito had purchased EM&E s21 bonds at a price of 97.5, what would have been the yield to

maturity? (6 points)

8.9%

d. Which company’s bonds would be the better buy: EM&E at 97.5 or Standard of California? (1 point)

Either, because their maturity levels are the same.

Score for A (52)

5. (48 points) Complete the following table. Show yield to maturity to one decimal place. (2 points for each

correct answer)

Discount 1Discount Average

Number Price or Years to Interest Annual 2Premium Principal Yield to

Purchased PaidPremium Maturity Rate Interest Amortization Invested Maturity

a. 8 105 $2400 5 8%

b. 10 97 1300 10 6%

c. 12 86 11,680 8 7.50%

d. 5 112 2600 3 10.20%

e. 1901100 5 7%

f. 20 102.5 2500 8 9.75%

9.32%20,250.00

262.50

$1,950.00

9.47%950.00

120.00

$ 70.00

5.85%5,300.00

2200.00

$ 510.00

9.95%11,160.00

1210.00

$ 900.00

6.40%9,850.00

130.00

$ 600.00

6.83%$8,200.00

$ 280.00

$ 640.00

d. $5,000 3 0.102 5 $510 annual interest

$600 4 3 5 $200 premium amortization

$5,000 3 1.12 5 $5,600 market value

($5,600 1 $5,000) 4 2 5 $5,300 average principal

($510 2 $200) 4 $5,300 5 0.058491, or 5.85%

e. $1,000 3 0.07 5 $70 annual interest

$100 4 5 5 $20 discount amortization

$1,000 3 0.90 5 $900 market value

($900 1 $1,000) 4 2 5 $950 average principal

($70 1$20) 4 $950 5 0.094737, or 9.47%

f. $20,000 3 0.0975 5 $1,950 annual interest

$500 4 8 5 $62.50 premium amortization

$20,000 3 1.025 5 $20,500 market price

($20,500 1 $20,000) 4 2 5 $20,250 average principal

($1,950 2 $62.50) 4 $20,250 5 0.09321, or 9.32%

Score for 5 (48)

Annuities

Chapter 23 Annuities 461

Learning Objectives

By studying this chapter and completing all assignments, you will be able to:

Compute the future value of an annuity.

Compute the regular payments of an annuity from the future value.

Compute the present value of an annuity.

Compute the regular payments of an annuity from the present value.

Compute the loan payment required to amortize a loan.

Create a loan amortization schedule.

Learning Objective

John and Joan Popplewell just won their state’s lottery and the prize was listed as

$5,000,000. When they purchased the winning ticket, they had a choice of taking the

prize over 20 years or taking one cash payment now. The $5,000,000 represents the sum

of 20 annual payments of $250,000 each. The series of equal payments is called an

annuity. Because they chose the single cash payment, they do not actually receive

$5,000,000 in cash. The amount that they receive is the present value of an annuity.

In Chapter 22, we discussed corporate and government bonds. When a corporation

issues $10,000,000 worth of 8%, 20-year bonds, the corporation is simply borrowing

money from the public for 20 years. Each $1,000 bond pays 8% (or $80) each year. The

$80 is paid out in two $40 payments every 6 months for 20 years. The series of $40 inter-

est payments is an annuity. The amount that someone pays for the bond is the present

value of the annuity. Some investors may worry that the corporation won’t have

$10,000,000 available in 20 years to repay the bonds. Therefore, the corporation may

decide to make 20 equal annual payments into a separate account managed by a neutral

third party. At the end of the 20 years, the deposits plus accumulated interest will be

worth the $10,000,000. This fund of deposits is called a sinking fund. Equal deposits

into a sinking fund form an annuity. The total amount is the future value of an annuity.

462 Part 6 Corporate and Special Applications

23.1 Chapter 16 must be covered be-

fore Chapter 23.

23.2 If consumers purchase on credit,

they must pay the interest.If they save

in advance for their purchases,they

will receive the interest.

An annuity is made up of a series of equal payments that occur at regular time intervals.

The payments go into—or come out of—an interest-bearing account or investment. The

constant interest rate is compounded at the same time the payments are made. (Perhaps

obviously, the number of periods in an annuity is the same as the number of payments.)

We can illustrate an annuity by drawing a straight line, called a time line. On the time

line, we insert equal marks and the payment dates, and write in the payment amounts.

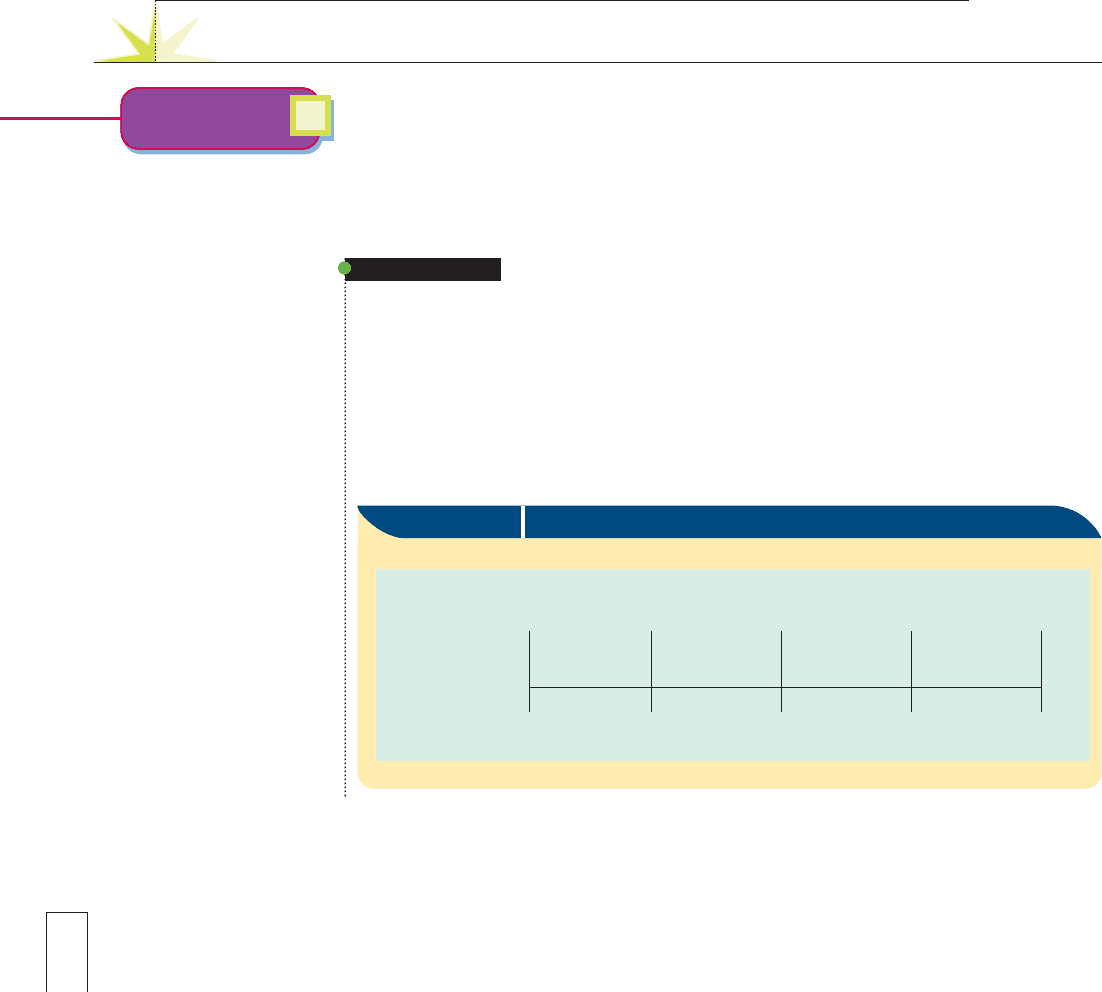
EXAMPLE A

An annuity has four annual payments of $1,000, always on December 31. The date of the

first $1,000 payment is December 31, 2010. Draw a time line showing the four years—

2010, 2011, 2012, and 2013—and the four payments.

The annuity illustrated in Figure 23-1, with the payments occurring at the end of

each period, is called an ordinary annuity. In this book, every annuity will have its

payments at the end of each period. The date December 31, 2009, is the beginning of

the annuity, and the date December 31, 2013, is the end of the annuity.

Learning Objective

Compute the future value of an

annuity.

23.3 In a very technical course,you

would emphasize that,for the basic ta-

bles and formulas to be used,(1) the

payments must be equal;(2) the pay-

ments must be regular;(3) the interest

rate must stay the same; and (4) the

compounding must coincide with the

payments.In this book,all of these de-

tails are assumed so that students can

concentrate on the fundamental

concept.

23.4 Another common type of annuity

is the annuity due, in which the pay-

ments come at the beginning of the

periods.Change Figure 23-1 so that the

first payment is on 12/31/09 but the

time line still stops at 12/31/13.An

example of an annuity due is a lease or

rental contract;you don’t move into an

apartment or office unless you pay at

least a month’s rent in advance of the

first month.We don’t cover annuities

due because the calculations aren’t

quite as straightforward.

Figure 23-1 Diagram of an Ordinary Annuity

Date

Period

Payment

12/31/09

1234

12/31/10

$1,000

12/31/11

$1,000

12/31/12

$1,000

12/31/13

$1,000

Again, the value of the annuity at the end of the annuity is called the future value of

the annuity. In example A, it is the total value of all payments plus the compound

Computing the Future Value of an Annuity

Chapter 23 Annuities 463

interest from the date of each payment until December 31, 2013. When a business or

individual decides to deposit the same amount of money every year (or month or quar-

ter) into an interest-bearing account for a specified amount of time, the future value of

the annuity is the amount that will be in the account when the last deposit is made.

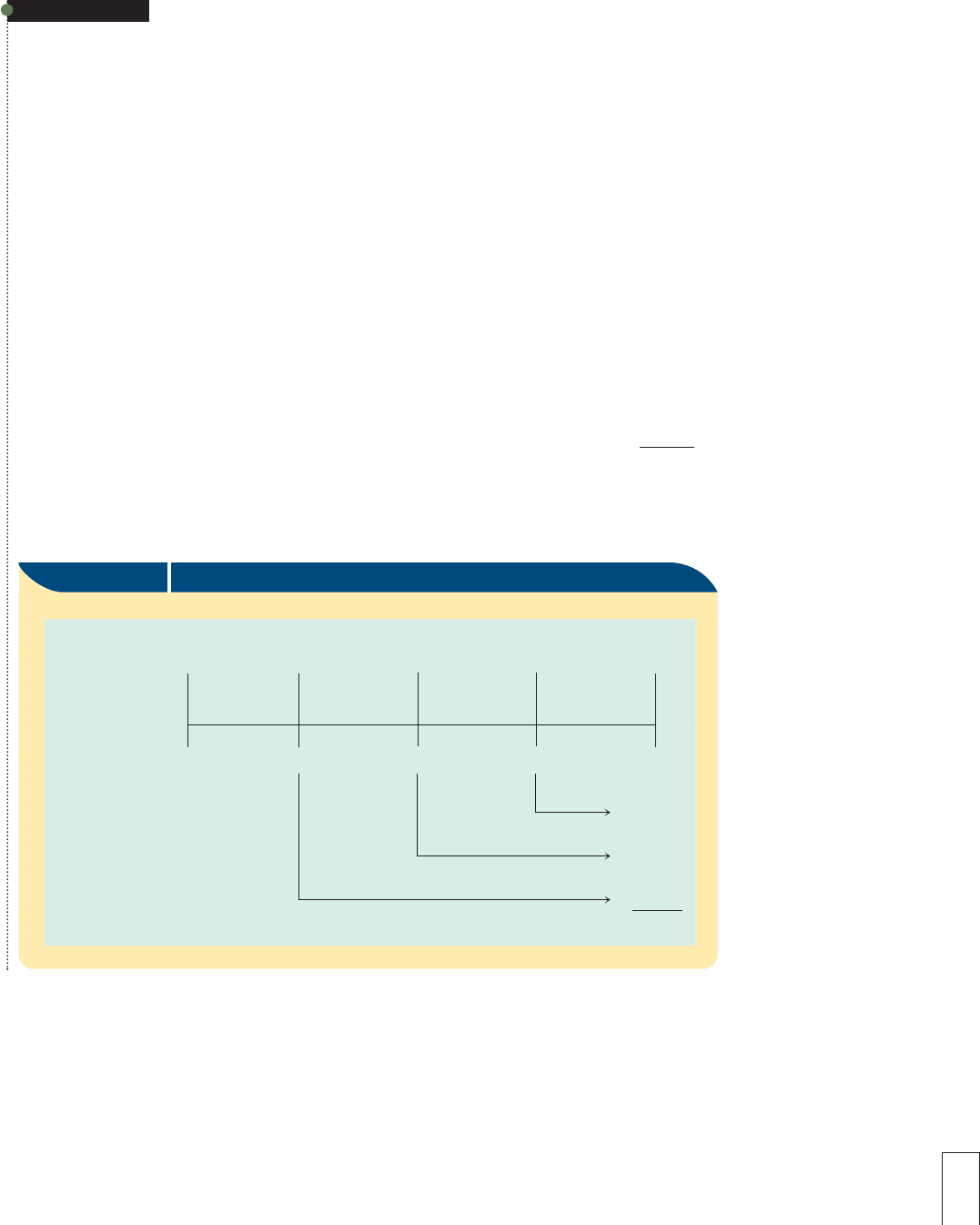
EXAMPLE B

In December, 2009, Mary Currie accepted a job with a manufacturing company. Mary

decided to save $1,000 at the end of each year for 4 years. The company credit union

allowed Mary to open a savings account on December 31, 2009, but Mary will not make

any deposit until December 31, 2010. She also will make deposits on December 31 of

2011, 2012, and 2013. The credit union pays interest of 10% compounded annually. How

much will be in the account after the last deposit? (Hint: Make a time line diagram and

compute the future value of each of the four deposits.)

To find the future value of the annuity on December 31, 2013, first use Table 16-1

(see Chapter 16) to determine the future value of each of the four payments as of

December 31, 2013. Then compute the total.

Amount of Date of Years of

ayment Payment Interest Future Value on 12/31/13

$1,000 12/31/10 3 $1,000 3 1.33100 5 $ 1,331

$1,000 12/31/11 2 $1,000 3 1.21000 5 $ 1,210

$1,000 12/31/12 1 $1,000 3 1.10000 5 $ 1,100

$1,000 12/31/13 0 $1,000 3 1.00000 511,000

Total 5 $ 4,641

Figure 23-2 illustrates how each of the four payments moves forward in time to

December 31, 2013.

23.5 Normally, a savings account

would not be opened without the

person making a deposit.But an annu-

ity has the same number of periods as

payments, so there must be a year

either before the first payment or after

the last one.Because we want the

payments to come at the end of each

period,the first year precedes the first

payment.Also,example B would be

more realistic if the deposits were

made monthly instead of annually.

23.6 A savings interest rate of 10%

per year may not be realistic in our

current economy.However,for teachers

who want to illustrate all of the

arithmetic,10% permits the easier

calculations.

Figure 23-2 Future Value of an Ordinary Annuity

12/31/13

$1,000

1,100

1,210

+1,331

$4,641

Date

Period

Payment

12/31/09

1234

12/31/10

$1,000

12/31/11

$1,000

12/31/12

$1,000

Future value of the annuity on 12/31/13 =

ANNUITY TABLES

Annuity calculations can be time-consuming, even with just four payments. With 20 or 30

payments, the calculations could be tiresome. Computers, financial calculators, and tables

eliminate tedious computations. Table 23-1, on pages 488–489, is an abbreviated sample of