De Felice F., Bini D. Classical Measurements in Curved Space-Times

Подождите немного. Документ загружается.

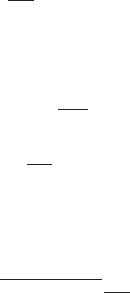
8.4 Special observers in Kerr space-time 183

so that the induced metric becomes

(2)

t,θ=const.



)

+(ω

ˆr

)

t,θ=const.

= γ(U, n)

φφ

dφ

+ g

. (8.185)

This in turn can be interpreted as the metric of a 2-surface corresponding to the

“image” of the space-time the observers U will construct once the embedding

of this surface in a ﬂat Euclidean or Minkowskian three-dimensional space is

considered.

Notice that the eﬀect of the relative velocity on the spatial geometry is to

increase the circumferences of circles by a gamma factor while keeping radial

distances ﬁxed.

To embed the 2-metric (8.185) in a ﬂat 3-metric, let us consider the ﬂat spatial

line element written in polar-like coordinates as

(3)

= ±dZ

+ dR

+ R

dφ

, (8.186)

where the plus sign refers to the Euclidean case and the minus sign to the

Minkowskian one. Let the embedding 2-surface be of the form Z = Z(R)so

that the corresponding induced metric becomes

(2)

= h

+ R

dφ

, (8.187)

where

= ±





+1, (8.188)

where the + sign refers to the Euclidean embedding and the − sign to the

Minkowskian one. Comparing (8.187) with (8.185), we deduce that

R(r)=γ(U, n)

√

φφ

= g





−2

. (8.189)

Integrating over the embedding surface Z = Z(R) and using as integration vari-

able the radial Boyer-Lindquist coordinate r, requiring R = R(r), we have

(r) ≡

(ss)



±(h

− 1)

dr, (8.190)

where r

(ss)

is a solution of the equation h

= 1 and therefore marks the

signature-switch point. Clearly Z

(ss)

) = 0. A general solution of (8.190)is

Z(r)=H(r −r

(ss)

(r)+H(r

(ss)

− r)Z

−

(r), (8.191)

where H is the Heaviside step function. Numerical integration easily gives the

form of the embedding diagram. This is shown in Fig. 8.3 for ZAMOs, static, and

Carter observers.

184 Observers in physically relevant space-times

Euclidean embedding

ZAMO

Static

Carter

Minkowskian embedding

(ss)

0.8

0.6

0.4

0.2

–0.2

–0.4

–0.6

–0.8

–1

2.2 2.4 2.6 2.8

r / M

Fig. 8.3. Relative embedding for selected families of observers on the equatorial

plane of Kerr space-time.

In the case of Kerr, the (ss) condition h

= 1, namely





−2

=1, (8.192)

can be analytically integrated to get the following expression for R:

(ss)

(r)=F (r; M,a,b) ≡

√

Δ+Mlog



r −M+

√

−M



+ b, (8.193)

where r

is the outer horizon and b is an arbitrary integration constant. From

(8.189)

and (8.193) we can deﬁne a new class of observers U

(ss)

characterized by

ν(U

(ss)

,n)=±



1 −

φφ

F (r; M,a,b)

. (8.194)

Assuming we have a maximally extended family of U

(ss)

observers (from the

horizon to spatial inﬁnity), the integration constant b is ﬁxed at b =2M since

(ss)

,n)

r=r

= 0. For a non-maximally extended family (i.e. from some observer

horizon radius r

∗

to inﬁnity) b would depend trivially on r

∗

8.5 Gravitational plane-wave space-time

The metric of a plane monocromatic gravitational wave, elliptically polarized and

propagating along a direction which we ﬁx as the x coordinate direction, can be

written in transverse-traceless (TT) gauge as

= −dt

+ dx

+(1− h

)dy

+(1+h

)dz

− 2h

dydz , (8.195)

8.5 Gravitational plane-wave space-time 185

where h

+/×

are functions only of (t − x). A physically reasonable observer who

could make a measurement is a geodesic one. The time-like geodesics of this

metric have been deduced in de Felice (1979); their 4-velocity has the form

(g)

[(1 + f + E

)∂

+(1+f −E

)∂

]

1 −h

− h

{[α(1 + h

)+βh

]∂

+[β(1 − h

)+αh

]∂

}, (8.196)

where α, β,andE are conserved Killing quantities and f = g

(g)

with

A, B =(2, 3), is equal to

f =(1− h

)



(g)



+(1+h

)



(g)



− 2h

(g)

 α

(1 + h

)+β

(1 −h

)+2αβh

, (8.197)

where  denotes the corresponding weak-ﬁeld limit, i.e. up to ﬁrst order in h

and h

Measurements in physically relevant space-times

The aim of modern astronomy is to uncover the properties of cosmic sources

by measuring their key parameters and deducing their dynamics. Black holes

are targets of particular interest for the role they have in understanding the

cosmic puzzles and probing the correctness of current theories. Black holes can be

considered simply as deep gravitational potential wells; therefore their existence

can only be inferred by observing the behavior of the surrounding medium. The

latter can be made of gas, dust, star ﬁelds, and obviously light, but all suﬀer

tidal strains and deformations which herald, out of the observer’s perspective,

the black hole’s existence and type. Essential tools for the acquisition of this

knowledge are the equations of relative acceleration which stand as basic seeds

for any physical measurement. We shall revisit them for speciﬁc applications, but

will always neglect electric charge in our discussion.

9.1 Measurements in Schwarzschild space-time

Consider a collection of particles undergoing tidal deformations; we shall deduce

how these would be measured by any particle of the collection, taken as a ﬁdu-

cial observer. Let us assume that the test particles of the collection move in

spatially circular orbits in Schwarzschild space-time whose metric is given by

(8.1). Indeed, the physical measurements which can be made in the rest frame

of the ﬁducial observer in the collection are the most natural to be performed in

satellite experiments.

Strain-induced rigidity

If U is a unitary time-like vector ﬁeld whose integral curves form a congruence

parameterized by the proper time τ

, then a connecting vector ﬁeld Y over

satisﬁes the condition

Y =0, (9.1)

9.1 Measurements in Schwarzschild space-time 187

and is a solution of Eq. (7.64), which we recall here:

dτ

= −R

βγδ

+ Y

∇

a(U)

. (9.2)

Given a ﬁeld of orthonormal frames {E

ˆα

},(9.2) can be written in tetrad compo-

nents as (see (7.78))

ˆa

+ K

(U, E)

ˆa

=0, (9.3)

where the deviation matrix K

(U, E)

ˆa

is given by

(U, E)

ˆa

=[T

(fw,U,E)

− S(U )+E(U)]

ˆa

. (9.4)

All quantities in (9.4) bear a physical meaning as we have already discussed in

Chapter 7: T

(fw,U,E)

is the twist tensor (deﬁned in (7.77)), S(U) is the Fermi-

Walker strain tensor (deﬁned in (7.76)), and E(U ) is the electric part of the

Riemann tensor.

Here we specify the vector ﬁeld U as being tangent to a family of equatorial

spatially circular orbits as in (8.110), that is

U =Γ(∂

+ ζ∂

), (9.5)

with Γ given by (8.27), with θ = π/2andζ = constant over C

Let us choose as a tetrad ﬁeld adapted to U the following (see (8.53)):

= U =Γ(∂

+ ζ∂

ˆr



1 −



1/2

∂

Γ(∂

ζ∂

), (9.6)

where

Γ=

Γζr

[1 −(2M/r)]

1/2

ζ =

ζr



1 −



. (9.7)

The various quantities involved are listed below.

(i) The physical components of the acceleration:

a(U)

ˆa

=Γ



1 −



1/2



− ζ



ˆaˆr

. (9.8)

(ii) The expansion tensor:

θ(U)

ˆa

≡ 0, (9.9)

showing that the above congruence is Born-rigid.

188 Measurements in physically relevant space-times

(iii) The vorticity vector, whose only non-vanishing component is

ω(U)

= −Γ



1 −



, (9.10)

and is coincident with the Fermi rotation vector ζ

(fw)

ˆa

(iv) The Fermi-Walker strain tensor S(U ), which, from (7.76), is given by

S(U)

ˆa

= ∇(U)

a(U)

ˆa

+ a(U)

ˆa

a(U)

= diag[S(U )

ˆrˆr

,S(U )

], (9.11)

where

S(U)

ˆrˆr

=Γ



(ζ

− ζ

)

Mr +(ζ

− ζ

)



1 −



1 −



−3ζ



1 −



− 3ζ



1 −



1 −



S(U)

=Γ



−

(ζ

− ζ

)



S(U)

= −MrΓ

(ζ

−

)(ζ

− ζ

), (9.12)

with



1 −



. (9.13)

(v) The twist tensor T

(fw,U,E)

which in our case, from (7.77), is given by

(fw,U,E)

ˆa

= δ

ˆa

(fw)

− ζ

ˆa

(fw)

− 2

ˆa

f ˆc

(fw)

ω(U)

ˆc

= diag[C, 0,C], (9.14)

where

C = ζ



1 −



= ||ζ

(fw)

. (9.15)

(vi) The electric part of the Riemann tensor E(U)

ˆa

(restricted to the equatorial

plane) which has only the following non-vanishing components:

E(U )

ˆrˆr

= −





1 −



+ ζ



E(U )



1 −



+2ζ



E(U )

. (9.16)

9.1 Measurements in Schwarzschild space-time 189

After some algebra, we obtain

ˆr

dτ







1 −



+ ζ



+ S(U )

ˆrˆr

+ C



ˆr

≡ 0,

dτ



−



2ζ



1 −



+ S(U )



≡ 0,

dτ



−

+ S(U )

+ C



≡ 0, (9.17)

consistent with the rigidity condition (9.9). The terms which ensure this rigidity

are the components of the Fermi-Walker strain tensor S(U)

(

i = r, θ, φ)which

balance the eﬀects of both the curvature and the centrifugal eﬀects generated

by the Fermi rotation of the tetrad (term C in (9.15) and (9.17)). Crucial to

this compensation is the requirement that the physical frame carried by the

observer (the ﬁducial particle of the system) is exactly the frame (9.6) all along

the orbit. The operational fulﬁllment of this requirement can only be achieved

if the observer is able to identify in his rest frame and without ambiguity the

radial, azimuthal, and latitudinal directions. A tetrad whose spatial axes remain

parallel to the above directions is termed phase-locked, as stated in (8.53)(de

Felice, 1991; de Felice and Usseglio-Tomasset, 1991). The relative strains S(U)

can be balanced by springs, for example, connecting discrete particles, or by the

internal structure of a conﬁguration like a star in the case of a ﬂuid. Let us now

see what information arises from a measurement of strains.

The radial direction is identiﬁed by the direction of the thrust when the orbit

is not a geodesic. In the case of a geodesic motion the thrust is zero; hence the

identiﬁcation of the frame (9.6) would require an approach diﬀerent from what we

shall pursue here. If the observer moves along a general spatially circular orbit, the

thrust is constant and, as stated, ﬁxes locally the radial direction with respect to

the center of the gravitational potential. Along this direction, the relative strain

S(U)

ˆrˆr

in (9.12) is always negative, meaning that the spring – or whatever other

mechanism one considers to ensure rigidity – exerts a compression (see Fig. 9.1).

This behavior is expected since in our case both the curvature and the Fermi

rotation cause a stretch at all values of r. However, the measurement of the

radial strain alone does not allow the observer to decide whether he is actually

moving in a circular orbit or is at rest with respect to the coordinate grid. This

uncertainty can be overcome with other types of measurements.

The azimuthal strain S(U)

can be written from (9.12)as

S(U)

= −ζ

(ζ

−

)(ζ

− ζ

)

[(1 −3M/r)/r

+(ζ

− ζ

)]

, (9.18)

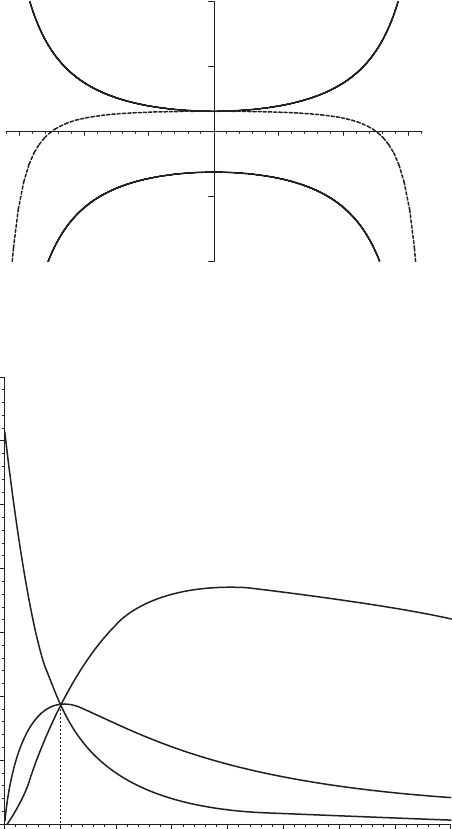
and its plot is shown in Fig. 9.1. It vanishes when ζ

= ζ

and ζ

, this being

the manifestation of an exact balancing of the curvature (tidal) compression with

the centrifugal stretch induced by the Fermi rotation. It is negative (meaning a

190 Measurements in physically relevant space-times

–0.1

–0.05

0.05

0.1

–0.15 –0.1 –0.05 0.05 0.1 0.15

ˆˆ

Fig. 9.1. Behavior of the relative strains S(U)

ˆr ˆr

(lower curve), S(U )

(upper

curve), and S(U)

(middle curve) as functions of ζ for ﬁxed values of r =4M.

The physical region is ζ

<ζ

0.14

0.12

0.08

0.06

0.04

0.02

234 5

III

r /M

∼

0.1

Fig. 9.2. The points with ζ

>ζ

≥ 0 are physically allowed equatorial circular

orbits in Schwarzschild space-time. The relative strains have diﬀerent signs in

the areas delimited by the curves ζ

,ζ

,andr =3M.

compression) when the centrifugal stretch overcomes the tidal compression, and

this occurs when

>ζ

and

<ζ

; it is positive (meaning

a stretch) when the tidal compression overcomes the centrifugal stretch, and

this occurs when ζ

<ζ

for r>3M and ζ

<ζ

for r<3M

(Fig. 9.2).

9.1 Measurements in Schwarzschild space-time 191

At r =3M we have ζ

ζ; hence S(U)

= ζ

, independent of ζ.

Since the Fermi rotation of the frame is zero at r =3M, the azimuthal strain

only needs to balance a tidal compression; hence the

φ-component of the tidal

curvature tensor is itself independent of ζ. The above result is consistent with the

independence of the thrust from ζ, as ﬁrst noticed by Abramowicz and Lasota

(1974). If the observer is at rest with respect to inﬁnity, i.e. if ζ = 0, then

S(U)

= ζ

> 0, meaning a stretch, so the measurement of this strain would

not help us understand whether the observer is at rest or not.

The relative strain in the latitudinal direction is, from (9.12), given by

S(U)

−

(ζ

− ζ

)

(ζ

− ζ

)

. (9.19)

As can be seen from Fig. 9.1, S(U)

is always positive, meaning that in the

θ direction a stretch is needed to ensure rigidity. If the observer is at rest,

then from (9.12) we would have S(U)

= ζ

= S(U)

> 0. In this case,

if one knows the local radial direction, the measurement of the strains in any

two directions orthogonal to each other and to the radial one would unambigu-

ously indicate that the observer is at rest, if these two strains are positive and

equal to each other, independent of rotation in the plane orthogonal to the radial

direction.

From the above analysis it follows that a direct measurement of the radial

S(U)

ˆrˆr

, latitudinal S(U)

, and azimuthal S(U)

strains allows one to deduce

in general that the observer is orbiting around a gravitational source (a black

hole, say), but they are not suﬃcient to let the observer recognize where in the

(ζ

,r)-plane of Fig. 9.2 he is actually orbiting. In fact, a measurement of the

azimuthal strain S(U)

would not allow the observer to distinguish between

orbiting with ζ in the range ζ

>ζ

and in the range ζ

>ζ

.In

both cases, in fact, S(U )

is negative (meaning a compression). Clearly, if he

can vary ζ and r then he would recognize that he was crossing the line ζ

in the (ζ

,r)-plane if S(U)

vanishes but not the thrust, implying that the

corresponding circular orbit is not a geodesic.

Partially constrained circular motion

Let us now relax the rigidity condition imposed on the collection of particles and

allow free motion in the

θ direction only. This condition is ensured by requiring

that a(U )

=0and∂

a(U)

=0foranyθ. This particular state of motion is

operationally set up by forcing the monitored particle to move inside a frictionless

narrowpipeﬁxedintheθ direction. Calculating the above constraints from (8.28)

and imposing the resulting condition in (9.17)

, the relative acceleration in the

θ direction becomes (de Felice and Usseglio-Tomasset, 1992)

192 Measurements in physically relevant space-times

dτ



−



2ζ



1 −



+Γ



1 −



(ζ

− ζ

)



= −ζ

. (9.20)

The particle appears to be acted on by an elastic type of force which pulls it

towards the equatorial plane if it was initially out of it. Then, a particle con-

strained to move inside a pipe without friction, aligned in an r = constant line

and perpendicular to the plane θ = π/2, will undergo harmonic oscillations with

a frequency equal to the proper frequency of the orbital revolution,

ζ|≡

dφ

dτ

= |ζ|Γ. (9.21)

Let us see what type of trajectory is described by the particle constrained in the

pipe.

In Schwarzschild space-time a geodesic, not conﬁned to the equatorial plane,

will lie on a plane which has some inclination with respect to the equatorial one.

The orbital plane is ﬁxed by the initial conditions. These can be expressed in

terms of:

(a) the conserved Killing quantities, namely ˜γ, the total energy in units of

(μ

being the particle mass and c the speed of light in vacuum), and λ,the

azimuthal angular momentum in units of μ

(b) the separation constant of the Hamilton-Jacobi equation Λ, which is the

total angular momentum in units of μ

These enter the geodesic equations, giving (de Felice and Clarke, 1990)

t =˜γ



1 −



−1

˙r = ±



˜γ

− 1+

−



1 −



1/2

θ = ±



−

sin



1/2

φ =

sin

, (9.22)

dot meaning derivative with respect to the proper time on the geodesics. The

requirement that the observer (the ﬁducial particle of the collection) moves on

a spatially circular geodesic conﬁned to the equatorial plane and with radius r

say, is summarized by the following conditions:

r = r

, ˙r =0,θ=

θ =0,

˜γ



1 −





1 −



, Λ



1 −



,λ

=Λ

. (9.23)