De Felice F., Bini D. Classical Measurements in Curved Space-Times
Подождите немного. Документ загружается.

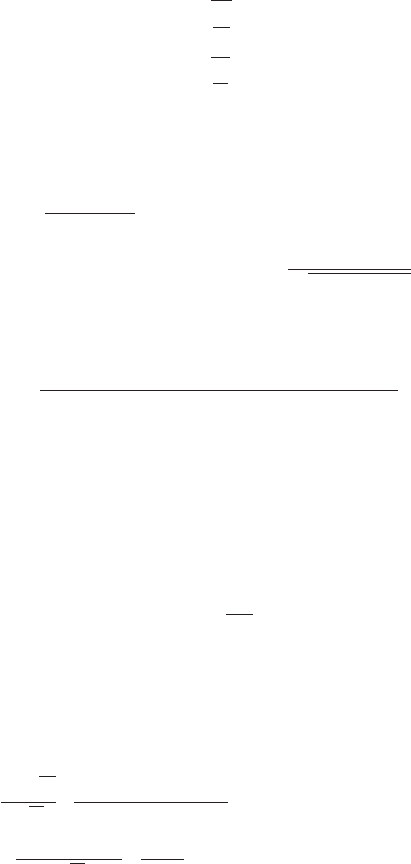
8.4 Special observers in Kerr space-time 173
A tetrad adapted to the observers U is given by
e(U)
ˆ
t
= U,
e(U)
ˆr
=
Δ
Σ
∂
r
,
e(U)
ˆ
θ
=
1
Σ
∂
θ
,
e(U)
ˆ
φ
=
¯
Γ[∂
t
+
¯
ζ∂
φ
], (8.117)
with
¯
ζ = −
g
tt
+ ζg
tφ
g
tφ
+ ζg
φφ
,
¯
Γ=(g
tt
+2
¯
ζg
tφ
+
¯
ζ
2
g
φφ
)
−1/2
=Γ
|g
tφ
+ ζg
φφ
|
g
2
tφ
− g
tt
g
φφ
. (8.118)
Explicitly, we have
¯
ζ =
Σ −2Mr(1 − aζ sin
2
θ)
sin
2
θ[ζ(r
2
+ a
2
)Σ −2aMr(1 − aζ sin
2
θ)]
. (8.119)
Note that, like U in (8.114), e(U)
ˆ
φ
can be written as
e(U)
ˆ
φ
= γ[ ||ν(U, n)||n + e(n)
ˆ
φ
]
=sinhα(U, n)n +cosα(U, n)e(n)
ˆ
φ
, (8.120)
so that, abbreviating α(U, n)=α, one has
e(U)
ˆ
φ
=
dU
dα
. (8.121)
The world lines with tangent vectors (8.110) have an acceleration vector
a(U)=a(U)
ˆr
e(U)
ˆr
+ a(U)
ˆ
θ
e(U)
ˆ
θ
, (8.122)
where
a(U)
ˆr
=
Γ
2
√
Δ
√
Σ
M(r
2
− a
2
cos
2
θ)
Σ
2
(1 −aζ sin
2
θ)
2
− rζ
2
sin
2
θ
,
a(U)
ˆ
θ
= −
Γ
2
sin θ cos θ
√
Σ
2Mr
Σ
2
[(r
2
+ a
2
)ζ −a]
2
+Δζ
2
. (8.123)
Moreover, orbits (8.110) in the special case ζ = constant over the entire congru-
ence (a more restrictive condition than the above mentioned £
U
ζ =0)forma
Born-rigid congruence of world lines (parameterized by r and θ) with vanishing
expansion tensor
θ(U)=0, (8.124)

174 Observers in physically relevant space-times
but with non-zero vorticity vector
ω(U)=ω(U )
ˆr
e(U)
ˆr
+ ω(U)
ˆ
θ
e(U)
ˆ
θ
, (8.125)
where
˜ω(U )
ˆr
=
1
2
Γ
¯
Γ
√
g
θθ
∂
θ
g
tt
+(ζ +
¯
ζ )∂
θ
g
tφ
+ ζ
¯
ζ∂
θ
g
φφ
,
˜ω(U )
ˆ
θ
= −
1
2
Γ
¯
Γ
√
g
rr
∂
r
g
tt
+(ζ +
¯
ζ )∂
r
g
tφ
+ ζ
¯
ζ∂
r
g
φφ
. (8.126)
In the general case (ζ = ζ(r, θ) varies over the congruence) the above relations
are modified: the congruence is no longer rigid and has
θ(U)
ˆr
ˆ
φ
=
1
2
[sgn(g
tφ
+ ζg
φφ
)] Γ
2
sin θ
Δ
√
Σ
∂
r
ζ,
θ(U)
ˆ
θ
ˆ
φ
=
1
2
[sgn(g
tφ
+ ζg
φφ
)] Γ
2
sin θ
Δ
Σ
∂
θ
ζ, (8.127)
where
ˆ
φ refers to the unit space-like direction e(U)
ˆ
φ
orthogonal to U.
Moreover, the components of the vorticity tensor change and one finds
ω(U)
ˆr
=˜ω
ˆr
+ θ(U )
ˆ
θ
ˆ
φ
,
ω(U)
ˆ
θ
=˜ω
ˆ
θ
− θ(U )
ˆr
ˆ
φ
, (8.128)
where we have denoted with a tilde the components (8.126) of the vorticity vector
corresponding to the case ζ = constant.
For a general circular orbit U, the Fermi-Walker gravitational force as measured
by a static observer m is given by
F
(G)
(fw,U,m)
= −
Dm
dτ
U
= −γ(U, m)[a(m)+ω(m) ×
m
ν(U, m)]
= −γ(U, m)[a(m)
ˆr
+ ω(m)
ˆ
θ
ν(U, m)
ˆ
φ
]e(m)
ˆr
−γ(U, m)[a(m)
ˆ
θ
− ω(m)
ˆr
ν(U, m)
ˆ
φ
]e(m)
ˆ
θ
, (8.129)
while that measured by a ZAMO observer n is given by
F
(G)
(fw,U,n)
= −
Dn
dτ
U
= −γ(U, n)[a(n)+θ(n) ν(U, n)]
= −γ(U, n)[a(n)
ˆr
+ θ(n)
ˆr
ˆ
φ
ν(U, n)
ˆ
φ
]e(n)
ˆr
−γ(U, n)[a(n)
ˆ
θ
+ θ(n)
ˆ
θ
ˆ
φ
ν(U, n)
ˆ
φ
]e(n)
ˆ
θ
. (8.130)

8.4 Special observers in Kerr space-time 175
Finally we identify a Frenet-Serret frame along U as the following:
E
ˆ
0
= U,
E
ˆ
1
=cosχe
ˆr
+sinχe
ˆ
θ
,
E
ˆ
2
= e(U)
ˆ
φ
=
dU
dα
,
E
ˆ
3
=sinχe
ˆr
− cos χe
ˆ
θ
= −
dE
1
dχ
, (8.131)
with
tan χ =
a(U)
ˆ
θ
a(U)
ˆr
,κ(U)
2
=[a(U )
ˆr
]
2
+[a(U)
ˆ
θ
]
2
, (8.132)
where a(U )
ˆr
and a(U )
ˆ
θ
are given by (8.123). The general expressions for τ (U)
1
and τ(U )
2
are rather complicated (Iyer and Vishveshwara, 1993). In order to
write these relations down explicitly let us introduce the following notation:
A = g
tt
+2ζg
tφ
+ ζ
2
g
φφ
,
B = g
tφ
+ ζg
φφ
, (8.133)
and
A
(ˆa)
= ∂
ˆa
g
tt
+2ζ∂
ˆa
g
tφ
+ ζ
2
∂
ˆa
g
φφ
,
B
(ˆa)
= ∂
ˆa
g
tφ
+ ζ∂
ˆa
g
φφ
, (8.134)
where a = r, θ and ∂
ˆa
=(g
aa
)
−1/2
∂
a
. Note that, according to our previous
notation,
A = −Γ
−2
, (sin χ, cos χ)=
1
2κ(U)A
A
(ˆr)
, A
(
ˆ
θ)
. (8.135)
It follows that
B =
1
2
∂
ζ
A, B
(ˆa)
=
1
2
∂
ζ
A
(ˆa)
. (8.136)
We then have the following compact expressions:
κ(U)
2
=
1
4
A
2
(ˆr)
+ A
2
(
ˆ
θ)
A
2
,
τ
1
(U)
2
=
B
2
16A
2
N
2
g
φφ
κ(U)
2
A
(ˆr)
B
(ˆr)
+ A
(
ˆ
θ)
B
(
ˆ
θ)
B
−
A
2
(ˆr)
+ A
2
(
ˆ
θ)
A
2
,
τ
2
(U)
2
=
1
16N
2
g
φφ
κ(U)
2
A
(ˆr)
B
(
ˆ
θ)
−A
(
ˆ
θ)
B
(ˆr)
A
2
. (8.137)
These relations can be further simplified. Using (8.136) in the expression of τ
1
(U)
2
yields
τ
1
(U)
2
=
A
2
4N
2
g
φφ
[∂
ζ
κ(U)]
2
(8.138)

176 Observers in physically relevant space-times
or, from (8.135),
τ
1
(U)
2
=
1
4Γ
4
N
2
g
φφ
[∂
ζ
κ(U)]
2
. (8.139)
Using relations (8.36) between ζ and ν(U, n)
ˆ
φ
and (8.116) for the Lorentz factor,
one can replace the derivative with respect to ζ with that with respect to ν,
obtaining
τ
1
(U)
2
=
1
4γ
4
[∂
ν
κ(U)]
2
. (8.140)
Finally, replacing ν with the rapidity parameter α, the above relation becomes
τ
1
(U)
2
=
1
4
[∂
α
κ(U)]
2
. (8.141)
A similar procedure, also using (8.135)forsinχ and cos χ, leads to the following
expression for τ
2
(U):
τ
2
(U)
2
=
1
4
κ(U)
2
[∂
α
χ]
2
. (8.142)
Using relations (8.137) and their simplifications (8.141) and (8.142), all the intrin-
sic geometrical properties of time-like spatially circular orbits can be easily stud-
ied. It is worth noting that the general expressions for curvature and torsions
given here are valid for any stationary and axisymmetric space-time.
Carter’s observers
A family of spatially circular orbits with particular properties was found by Carter
(1968). Their tangent vector fields are given by
u
(car)
=
r
2
+ a
2
√
ΔΣ
∂
t
+
a
r
2
+ a
2
∂
φ
,
u
(car)
= −
Δ
Σ
dt −a sin
2
θdφ
. (8.143)
These belong to the class of spatial circular orbits with
ζ
(car)
=
a
r
2
+ a
2
. (8.144)
The main property of these trajectories is that of being the unique time-like world
lines belonging to the intersection of the Killing 2-plane (t, φ) with the 2-plane
spanned by Kerr principal null directions.
The direction orthogonal to u
(car)
in the (t, φ)-plane is given by
¯u
(car)
=
a sin θ
√
Σ
∂
t
+
1
a sin
2
θ
∂
φ
,
¯u
(car)
= −
a sin θ
√
Σ
dt −
r
2
+ a
2
a
dφ
. (8.145)
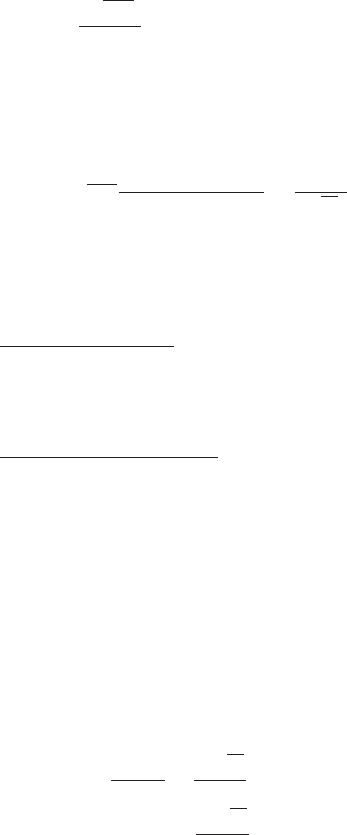
8.4 Special observers in Kerr space-time 177
An orthonormal frame adapted to the Carter family of observers is the same as
the one in (8.117), with ζ replaced by ζ
(car)
:
E(u
(car)
)
ˆ
t
= u
(car)
,E(u
(car)
)
ˆr
= e
ˆr
,
E(u
(car)
)
ˆ
θ
= e
ˆ
θ
,E(u
(car)
)
ˆ
φ
=¯u
(car)
. (8.146)
With respect to this frame, the principal null directions (8.86) of Kerr space-time
take the form
k
±
=
√
ΔΣ
r
2
+ a
2
u
(car)
± e
ˆr
; (8.147)
this implies that photons moving along the above directions will appear spatially
radial with respect to Carter’s observers. If we analyze the vector field u
(car)
with respect to the static observers in Kerr space-time, we find, for the relative
velocity,
ν(u
(car)
,m)
ˆ
φ
=
√
γ
φφ
ζ
(car)
M(1 − M
φ
ζ
(car)
)
=
a sin θ
√
Δ
, (8.148)
where M, M
φ
,andγ
φφ
are defined by (8.89) and (8.90).
Furthermore, Carter’s observers measure the electric and magnetic parts of the
Weyl tensor as parallel to each other:
E(u
(car)
)=
Mr(r
2
− 3a
2
cos
2
θ)
Σ
3
[−2e
ˆr
⊗ e
ˆr
+ e
ˆ
θ
⊗ e
ˆ
θ
+¯u
(car)
⊗ ¯u
(car)
],
(8.149)
H(u
(car)
)=
Ma cos θ(3r
2
− a
2
cos
2
θ)
Σ
3
[−2e
ˆr
⊗ e
ˆr
+ e
ˆ
θ
⊗ e
ˆ
θ
+¯u
(car)
⊗ ¯u
(car)
].
Null spatially circular orbits
Null spatially circular orbits cannot be associated with a physical observer;
nonetheless they play an important role as critical conditions for time-like tra-
jectories. Their tangent vector field is given by
=Γ
(null)
(∂
t
± ζ
(null)
±
∂
φ
), (8.150)
with
ζ
(null)
±
=
2aMr
A
±
Σ
√
Δ
sin θA
= ζ
(ZAMO)
±
Σ
√
Δ
sin θA
, (8.151)
where A is given by (8.75) and Γ
(null)
is an arbitrary factor; ζ
(ZAMO)
is given by
(8.113).

178 Observers in physically relevant space-times
Observers on equatorial circular orbits
There exists a whole collection of special circular orbits in the equatorial plane.
They are the corotating (+) and counter-rotating (−) time-like circular geodesics
whose angular and linear velocities (with respect to ZAMOs) are respectively
3
ζ
K±
≡ ζ
±
=
a ±(r
3
/M)
1/2
−1
, (8.152)
ν
K±
≡ ν
±
=
a
2
∓ 2a
√
Mr + r
2
√
Δ(a ±r
r/M)
. (8.153)
These become null when |ν
±
| = 1, which occurs at
r
(null)
K±
=2M
1 + cos
2
3
arccos
∓
a
M
. (8.154)
Obviously co- and counter-rotating time-like circular geodesics exist at r>r
(null)
K+
and r>r
(null)
K−
respectively.
Closely related to these are the geodesic meeting point (gmp) orbits defined by
the intersection points of the time-like geodesics, with velocity
ν
(gmp)
=
ν
+
+ ν
−
2
= −
aM(3r
2
+ a
2
)
√
Δ(r
3
− a
2
M)
. (8.155)
Similarly one may consider special orbits having spatial 3-velocity (with respect
to ZAMOs) given by
ν
(pt)
=
2
ν
−1
+
+ ν
−1
−
=
(r
2
+ a
2
)
2
− 4a
2
Mr
a
√
Δ(3r
2
+ a
2
)
. (8.156)
Both the above families of orbits play a role in the study of parallel transport
(pt) of vectors along circular orbits (Bini, Jantzen, and Mashhoon, 2002).
The linear velocities of the circular geodesics and gmp orbits are related to the
ZAMO kinematical quantities
a(n)
ˆr
=
MΔ
−1/2
(r
2
+ a
2
)
2
− 4a
2
Mr
r
2
(r
3
+ a
2
r +2Ma
2
)
,
θ(n)
ˆr
ˆ
φ
=
Ma(3r
2
+ a
2
)
r
2
(r
3
+ a
2
r +2Ma
2
)
,
k
(lie)
(n)
ˆr
= −
(r
3
− a
2
M)
√
Δ
r
2
(r
3
+ a
2
r +2a
2
M)
, (8.157)
by
a(n)
ˆr
= k
(lie)
(n)
ˆr
ν
+
ν
−
,θ(n)
ˆ
φˆr
= −k
(lie)
(n)
ˆr
ν
(gmp)
, (8.158)
where k
(lie)
(n)
ˆr
= −∂
ˆr
ln
√
g
φφ
, as follows from the definition (3.169).
3
To simplify notation in this section we use U
±
to denote the 4-velocity of corotating and
counter-rotating geodesics as well as ν
±
and ζ
±
for their relative and angular velocities,
dropping the symbol K.

8.4 Special observers in Kerr space-time 179
On the equatorial plane, the expressions of the gravitational force given in
(8.129) and (8.130) on general spatially circular orbits reduce to
F
(G)
(fw,U,m)
= −γ(U, m)[a(m)
ˆr
+ ω(m)
ˆ
θ
ν(U, m)
ˆ
φ
]e(m)
ˆr
(8.159)
as measured by the static observer m,and
F
(G)
(fw,U,n)
= −γ(U, n)[a(n)
ˆr
+ θ(n)
ˆr
ˆ
φ
ν(U, n)
ˆ
φ
]e(n)
ˆr
(8.160)
as measured by a ZAMO observer n.
We now have expressions for all the geometrical and kinematical quantities
which are needed to specify the Frenet-Serret, Fermi-Walker, and parallel prop-
agated frames.
The Frenet-Serret frame is given by (8.131) with χ =0,thatis
E
0
=coshαn+sinhαe
ˆ
φ
,E
1
= e
ˆr
,
E
2
=sinhαn+coshαe
ˆ
φ
,E
3
= −e
ˆ
θ
, (8.161)
recalling that ν = tanh α, γ =coshα. The second torsion τ
2
vanishes, while the
geodesic curvature κ and the first torsion τ
1
are given by
κ =
√
ΔM
r
3
Γ
2
ζ
2
a −
1
ζ
2
−
r
3
M
,
τ
1
=
Γ
2
r
Ma
r
2
− ζ
M(r
2
+2a
2
)
r
2
− r
1 −
2M
r
+ ζ
2
Ma(3r
2
+ a
2
)
r
2
. (8.162)
Equivalently, we have
κ = k
(lie)
(n)
ˆr
γ
2
(ν − ν
+
)(ν − ν
−
),
τ
1
= k
(lie)
(n)
ˆr
ν
(gmp)
γ
2
(ν − ν
(crit)+
)(ν − ν
(crit)−
), (8.163)
where
ν
(crit)±
=
γ
−
ν
−
∓ γ
+
ν
+
γ
−
∓ γ
+
= −
1
2Ma(3r
2
+ a
2
)
√
Δ
−2a
2
M(a
2
− 3Mr)
+ r
2
(r
2
+ a
2
)(r − 3M)
±(r
3
+ a
2
r +2a
2
M)
√
r
r(r − 3M)
2
− 4a
2
M
, (8.164)
or equivalently
ζ
(crit)±
=
Γ
−
ζ
−
∓ Γ
+
ζ
+
Γ
−
∓ Γ
+
, (8.165)
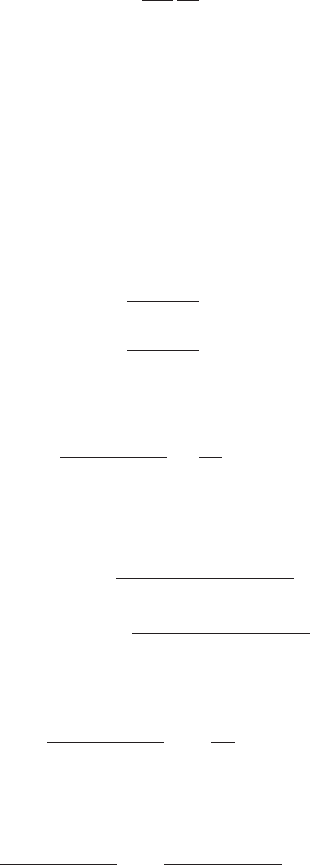
180 Observers in physically relevant space-times
identify those orbits on which the first torsion vanishes. The notation “crit” for
the observers moving along equatorial circular orbits comes from the relation
τ
1
= −
1
2γ
2
dκ
dν
, (8.166)
which can be easily verified; critical observers have vanishing first torsion and
hence extreme acceleration (in magnitude) and are termed extremely accelerated
observers.
The time-like condition |ν
(crit)+
| < 1 is satisfied when r
+
<r<r
(null)
K+
while
|ν
(crit)−
| < 1 when r>r
(null)
K−
.
We can now specify the geometrical properties of extremely accelerated
observers. Consider for example the U
(crit)−
orbits (analogous considerations hold
for the U
(crit)+
orbits). From Eq. (8.164) it follows that
ν
+
− ν
(crit)−
=
γ
−
γ
−
− γ
+
(ν
+
− ν
−
),
ν
−
− ν
(crit)−
=
γ
+
γ
−
− γ
+
(ν
+
− ν
−
), (8.167)
and therefore
ν
+
− ν
(crit)−
ν
−
− ν
(crit)−
=
γ
−
γ
+
. (8.168)
Similarly we find
1 −ν
+
ν
(crit)−
=
γ
+
γ
−
(1 −ν
+
ν
−
) −1
γ
+
(γ
−
− γ
+
)
,
1 −ν
−
ν
(crit)−
= −
γ
+
γ
−
(1 −ν
+
ν
−
) −1
γ
−
(γ
−
− γ
+
)
, (8.169)
so that
1 −ν
+
ν
(crit)−
1 −ν
−
ν
(crit)−
= −
γ
−
γ
+
. (8.170)
Combining (8.168) and (8.170) one has
ν
+
− ν
(crit)−
1 −ν
+
ν
(crit)−
= −
ν
−
− ν
(crit)−
1 −ν
−
ν
(crit)−
. (8.171)
Recalling the relativistic formula for the addition of velocities, the above relation
implies
ν(U
+
,U
(crit)−
)=−ν(U
−
,U
(crit)−
), (8.172)
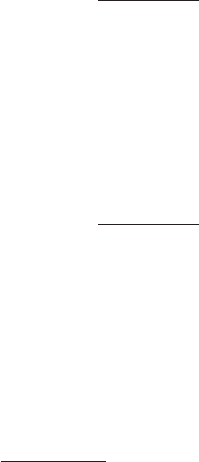
8.4 Special observers in Kerr space-time 181
that is, the U
(crit)−
observers are so special that with respect to them the
spatial geodesic velocities differ only by a sign. Therefore, splitting of co- and
counter-rotating geodesics by U
(crit)−
observers gives
U
+
= γ(U
+
,U
(crit)−
)[U
(crit)−
+ ν(U
+
,U
(crit)−
)
¯
U
(crit)−
],
U
−
= γ(U
+
,U
(crit)−
)[U
(crit)−
− ν(U
+
,U
(crit)−
)
¯
U
(crit)−
], (8.173)
where
¯
U
(crit)−
is the unit spatial vector orthogonal to U
(crit)−
in the Killing
2-plane (∂
t
,∂
φ
). By adding these equations one gets
U
+
+ U
−
=2γ(U
+
,U
(crit)−
)U
(crit)−
(8.174)
or, equivalently,
U
(crit)−
=
U
+
+ U
−
||U
+
+ U
−
||
, (8.175)
which is the most significant characterization of these observers. Since a similar
result is obtained by the observers U
(crit)+
when measuring the spatial velocities
of the circular geodesics U
+
and U
−
, we deduce that, as a sort of compensation,
the gravitational drag does not affect the measurements themselves. Repeating
the above derivation for the U
(crit)+
observers, we can write the more general
relation
U
(crit)±
=
U
+
∓ U
−
||U
+
∓ U
−
||
. (8.176)
Extremely accelerated observers on the equatorial plane are also special
because the vanishing of the first torsion of their orbits together with the identi-
cal vanishing of the second torsion makes the whole Frenet-Serret angular veloc-
ity vanish. In other words the natural Frenet-Serret frame adapted to U
(crit)±
observers is also a Fermi-Walker frame, i.e. with spatial axes aligned with the
axes of a gyroscope. In particular the unit vector of the φ direction is such that
D
(fw,U
(crit)±
)
dτ
U
(crit)±
¯
U
(crit)±
=0, (8.177)
or, equivalently,
∇
U
(crit)±
¯
U
(crit)±
=0, (8.178)
because
¯
U
(crit)±
·U
(crit)±
=0anda(U
(crit)±
) ·
¯
U
(crit)±
= 0, since the acceleration
has only a radial component.
Another interesting geometrical property of the extremely accelerated
observers – a consequence of the above result – concerns their relationship with
any other equatorial circular orbit u. One can prove the following statement:
“As seen by extremely accelerated observers, any equatorial circular orbit u is
relatively straight,” that is, its relative Fermi-Walker curvature is zero. In fact,

182 Observers in physically relevant space-times
we have
ˆ
V(u, U
(crit)±
)=−ˆν(u, U
(crit)±
)=
¯
U
(crit)±
. Therefore, from (4.46) for the
comoving relative Frenet-Serret frames and taking into account (8.177), we have
D
(fw,U
(crit)±
)
d
U
(crit)±
¯
U
(crit)±
= K
(fw,u,U
(crit)±
)
N
(fw,u,U
(crit)±
)
=0, (8.179)
where the factor γ(u, U
(crit)±
)ν(u, U
(crit)±
) has been re-absorbed in the parameter
U
(crit)±
; hence, K
(fw,u,U
(crit)±
)
=0.
Observer-dependent embedding diagrams in Kerr space-time
Two-dimensional embedding diagrams have proven to be very valuable in visu-
alizing certain aspects of space-time geometry in stationary axially symmetric
space-times. However, an embedding diagram, as well as the associated space-
time image, is observer-dependent. In what follows we shall consider families
of observers in motion along spatially circular orbits on the equatorial plane
of Kerr space-time and study how they would see the black hole space-time
geometry. Some of these, including static, ZAMO, geodesic, Carter, geodesic
meeting point, Lie/Fermi-Walker relatively and comoving relatively straight, and
extremely accelerated, have already been extensively studied. In the analysis we
are going to perform, certain “new” special families of observers arise.
Let us consider spatially circular orbits in the equatorial plane of Kerr space-
time, with tangent vector fields written with respect to ZAMO observers as
U = γ(U, n)[n + ||ν(U, n)||ˆν(U, n)], (8.180)
with
ˆν(U, n)=
1
√
g
φφ
∂
φ
, ˆν(U, n)
=
√
g
φφ
(dφ + N
φ
dt),
||ν(U, n)|| =
−g
tt
g
φφ
ζ +
g
tφ
g
φφ
. (8.181)
Let
¯
U be (minus) the unit vector of the relative velocity of n with respect to U,
¯
U
= −ˆν(n, U )
= γ(U, n)[||ν(U, n)||n
+ˆν(U, n)
], (8.182)
and ω
ˆr
=
√
g
rr
dr a unit 1-form in the radial direction. Then the set {U
,ω
ˆr
,
¯
U
}
forms a U-adapted tetrad in the equatorial plane. With respect to the above
frame the metric element can be written as
ds
2
= −(U
)
2
+(
¯
U
)
2
+(ω
ˆr
)
2
. (8.183)
Since n
= −Ndt,onat = constant and θ = constant slice of LRS
U
,(
¯
U
)
2
reduces to
(
¯
U
)
2
|
t,θ=const.
=[γ
(U,n)
√
g
φφ
dφ]
2
, (8.184)
