De Felice F., Bini D. Classical Measurements in Curved Space-Times
Подождите немного. Документ загружается.

8.2 Special observers in Schwarzschild space-time 163
E
ˆ
0
= U,
E
ˆ
1
=cosχe
ˆr
+sinχe
ˆ
θ
,
E
ˆ
2
= E
ˆ
φ
,
E
ˆ
3
=sinχe
ˆr
− cos χe
ˆ
θ
, (8.57)
with
tan χ = −
ζ
2
sin θ cos θ
M
r
3
− ζ
2
sin
2
θ
1 −
2M
r
1/2
= −
R
r
ζ
2
cos θ
(ζ
2
K
− ζ
2
sin
2
θ)
. (8.58)
The Frenet-Serret curvature and torsions are then given by
κ(U)
2
=Γ
4
r
2
1 −
2M
r
ζ
2
K
− ζ
2
sin
2
θ
2
+ ζ
4
sin
2
θ cos
2
θ
,
implying also that
τ
1
(U)
2
=
Γ
4
ζ
2
sin
2
θ
1 −
2M
r
ζ
2
K
− ζ
2
sin
2
θ
1 −
3M
r
− ζ
2
cos
2
θ
2
1 −
2M
r
(ζ
2
K
− ζ
2
sin
2
θ)
2
+ ζ
4
sin
2
θ cos
2
θ
,
τ
2
(U)
2
=
ζ
2
M
2
cos
2
θ
r
6
1 −
2M
r
(ζ
2
K
− ζ
2
sin
2
θ)
2
+ ζ
4
sin
2
θ cos
2
θ
. (8.59)
Observers on equatorial spatially circular orbits
Let us now require that the plane of the orbits in Schwarzschild space-time is
fixed at θ = π/2, referred to as the equatorial plane; we shall still confine our
attention to spatially circular orbits. For these orbits the acceleration is only
radial, as follows from (8.28), that is
a(U)=
1 −
2M
r
− ζ
2
r
2
−1
1 −
2M
r
1/2
r(ζ
2
K
− ζ
2
) e
ˆr
= −|ζ
c
|
ζ
2
− ζ
2
K
ζ
2
c
− ζ
2
e
ˆr
, (8.60)
where
|ζ
c
| =
1
r
1 −
2M
r
1/2
=
1
R
. (8.61)
This family of orbits is expansion-free and has a vorticity vector given by
ω(U)=−Γ
2
ζr
1 −
3M
r
e
ˆ
θ
. (8.62)

164 Observers in physically relevant space-times
In Chapter 4 we discussed relative Frenet-Serret frames and introduced in
(4.39) the quantity k
(fw,U,m)
as the Fermi-Walker curvature of the orbit, that is
D
(fw,U,m)
d
(U,m)
ˆν(U, m)=k
(fw,U,m)
ˆη
(fw,U,m)
. (8.63)
Similarly, when the Lie-spatial (instead of Fermi-Walker) temporal derivative is
involved, one has the Lie-relative curvature k
(lie,U,m)
D
(lie,U,m)
d
(U,m)
ˆν(U, m)=k
(lie,U,m)
ˆη
(lie,U,m)
. (8.64)
In this case, C
m
being vorticity-free and expansion-free, we have, from (3.63),
k
(fw,U,m)
= k
(lie,U,m)
. (8.65)
A direct calculation gives
k
(lie,U,m)
= −
1
r
1 −
2M
r
1/2
= −
1
R
, (8.66)
clarifying the geometrical meaning of the effective radius introduced in (8.39);
hereafter k
(lie,U,m)
will be abbreviated simply as k
(lie)
. We then have, from (8.36)
and (8.60),
a(U)=k
(lie)
ζ
2
− ζ
2
K
ζ
2
c
− ζ
2
e
ˆr
= k
(lie)
γ
2
ν
2
− ν
2
K
e
ˆr
, (8.67)
where ν
K
= ν(U
K±
,m) is the Keplerian relative velocity,
ν
K
=
M
r − 2M
1/2
. (8.68)
The Frenet-Serret frame (8.53) in this case implies a second torsion identically
zero, namely τ
2
(U) = 0, and
κ(U)=Γ
2
1 −
2M
r
1/2
M−r
3
ζ
2
r
2
=Γ
1 −
2M
r
R(ζ
2
K
− ζ
2
),
τ
1
(U)=ζΓ
2
1 −
3M
r
, (8.69)
with
tan χ =0, (8.70)

8.3 Kerr space-time 165
and hence E
ˆ
1
= e
ˆr
. We see that, like U , a(U ) forms a one-parameter family of
vectors, the parameter being the angular velocity ζ (or equivalently the spatial
velocity or the rapidity with respect to any family of observers). Expressing κ(U)
and τ
1
(U) in terms of the rapidity α with respect to the family of static observers
gives
κ(U)=
k
(lie)
cosh
2
α
K
sinh(α −α
K
)sinh(α + α
K
),
τ
1
(U)=−
1
2
∂
α
κ(U), (8.71)
where α
K
= α(U
K
,m) and tanh α
K
= ν
K
.
One can then consider the extremely accelerated orbits as those equatorial
spatially circular orbits satisfying the condition
∂
ζ
||a(U)|| =0. (8.72)
A direct calculation shows that these orbits coincide here with those of the static
observers, i.e. with ζ =0.
8.3 Kerr space-time
The Kerr metric is described by the line element
ds
2
= −dt
2
+
2Mr
Σ
(a sin
2
θdφ − dt)
2
+(r
2
+ a
2
)sin
2
θdφ
2
+
Σ
Δ
dr
2
+Σdθ
2
, (8.73)
where
Σ=r
2
+ a
2
cos
2
θ, Δ=r
2
+ a
2
− 2Mr. (8.74)
It is useful to introduce the quantity
A =(r
2
+ a
2
)
2
− Δa
2
sin
2
θ (8.75)
such that g
φφ
= A sin
2
θ/Σ . The parameters M and a describe the total mass and
specific angular momentum of the source, respectively. The Kerr metric describes
the space-time of a rotating black hole when a<M. In this case the coordinates
in (8.73)runast ∈ (−∞, +∞), r ∈ (r
+
, ∞), θ ∈ [0,π], φ ∈ [0, 2π], with
r
+
= M +
M
2
− a
2
. (8.76)

166 Observers in physically relevant space-times
These are spherical-like coordinates known as Boyer-Lindquist coordinates.The
inverse Kerr metric is given by
∂
∂s
2
=
1
Σ
)
−
A
Δ
∂
∂t
2
−
4Mra
Δ
∂
∂t
∂
∂φ
+
Δ −a
2
sin
2
θ
Δsin
2
θ
∂
∂φ
2
+Δ
∂
∂r
2
+
∂
∂θ
2
*
. (8.77)
Kerr space-time admits two Killing vectors, which in Boyer-Lindquist coordinates
are given by
ξ
0
= ∂
t
,ξ
3
= ∂
φ
. (8.78)
They express the properties of stationarity and axial symmetry of the solution.
Various coordinate patches
Themetricform(8.73) reduces to the Schwarzschild metric if we set a =0.The
surface r = r
+
, where Δ = 0, is a coordinate singularity representing the space-
like boundary of an event horizon.
1
It can be removed with a suitable change of
coordinates. The same type of coordinates introduced in the Schwarzschild case
have been extensively investigated in the literature (see de Felice and Clarke,
1990) and we shall not repeat them here. We shall instead analyze in more detail
the following coordinate system, named after Painlev´e and Gullstrand.
The Painlev´e-Gullstrand coordinates X
α
≡ (T,R,Θ, Φ) are related to the
Boyer-Lindquist coordinates by the transformation
T = t −
!
r
f(r)dr , Φ=φ −
!
r
a
r
2
+ a
2
f(r)dr ,
R = r, Θ=θ, (8.79)
where
f(r)=−
2Mr(r
2
+ a
2
)
Δ
. (8.80)
The Kerr metric in Painlev´e-Gullstrand coordinates takes the form
ds
2
= −
1 −
2Mr
Σ
dT
2
+2
2Mr
r
2
+ a
2
dT dr
−
4aMr
Σ
sin
2
θdTdΦ+sin
2
θ
(r
2
+ a
2
)+
2a
2
Mr
Σ
sin
2
θ
dΦ
2
−2a sin
2
θ
2Mr
r
2
+ a
2
dr dΦ+
Σ
(r
2
+ a
2
)
dr
2
+Σdθ
2
, (8.81)
1
The surface r = r
+
is an outer boundary since Δ = 0 admits also the solution
r
−
= M−
√
M
2
− a
2
, which is the inner boundary of the event horizon. The inner
structure of the Kerr black hole will not be considered here.

8.3 Kerr space-time 167
which is clearly regular on r = r
+
.Thea = 0 limit of (8.81)is(8.11), as expected.
The induced metric on T = constant slices is non-diagonal and has the form
ds
2
|
T = const.
=sin
2
θ
(r
2
+ a
2
)+
2Mra
2
Σ
sin
2
θ
dΦ
2
−2a sin
2
θ
2Mr
r
2
+ a
2
dr dΦ
+
Σ
(r
2
+ a
2
)
dr
2
+Σdθ
2
. (8.82)
The most interesting observers in the Painlev´e-Gullstrand coordinate represen-
tation are those with world lines orthogonal to the T = constant hypersurfaces.
They have 4-velocity
N
= −dT, N = ∂
T
−
2Mr(r
2
+ a
2
)
Σ
∂
r
, (8.83)
and form a geodesic (a(N) = 0) and vorticity-free (ω(N) = 0) congruence but
have a non-vanishing expansion.
Curvature invariants
There are two quadratic curvature Weyl invariants,
2
K
1
= R
αβγδ
R
αβγδ
,K
2
= R
αβγδ ∗
R
αβγδ
; (8.84)
in Boyer-Lindquist coordinates they are given by
K
1
=
48M
2
Σ
6
(r
2
− a
2
cos
2
θ)(Σ
2
− r
2
a
2
cos
2
θ),
K
2
= −
96M
2
ra cos θ
Σ
6
(3r
2
− a
2
cos
2
θ)(r
2
− 3a
2
cos
2
θ) . (8.85)
The invariant K
2
is a rotationally induced quantity and its measurement, if oper-
ationally feasible, would unambiguously ascertain that we are in a rotating space-
time (Ciufolini and Wheeler, 1995). An unavoidable curvature singularity is found
where Σ = 0, i.e. where r =0andθ = π/2.
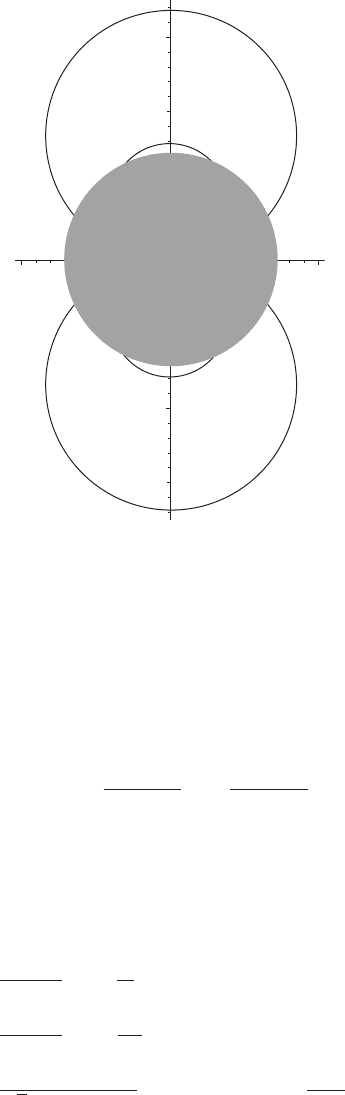
The forms (8.85) of the curvature invariants show that these quantities change
their signs several times if one moves along θ = constant hypersurfaces; see
Fig. 8.2. These invariants can be calculated down to the ring singularity, and
one can deduce that they tend to the singularity with different asymptotic values
according to how they approach it. This shows that the Kerr singularity has
directional properties.
2
Since the Kerr metric is a vacuum solution, the Weyl and Riemann tensors coincide.
168 Observers in physically relevant space-times
3
2
z
–2
–2
–3
2
Fig. 8.2. Curvature invariants K
1
and K
2
in Kerr space-time, evaluated for
a/M =0.5andM = 1. The curves represent the points where the invariants
vanish. The closest curve to the horizon (circle in gray) is that of K
2
.
Principal null directions,
Petrov type and principal complex null frame
The Kerr metric admits two independent principal null directions whose tangent
vectors are given by
k
±
= ∂
t
±
Δ
(r
2
+ a
2
)
∂
r
+
a
(r
2
+ a
2
)
∂
φ
. (8.86)
The Kerr metric is of Petrov type D. Associated with the above principal null
directions is a complex null frame which can be fixed, leaving the two real null
vectors to be aligned with the vectors (8.86) and the two complex conjugate
vectors m and ¯m as follows (Wald, 1984):
l ≡
r
2
+ a
2
Δ
k
+
=
1
Δ
(r
2
+ a
2
)∂
t
+Δ∂
r
+ a∂
φ
,
n ≡
r
2
+ a
2
2Σ
k
−
=
1
2Σ
(r
2
+ a
2
)∂
t
− Δ∂
r
+ a∂
φ
,
m =
1
√
2(r + ia cos θ)
ia sin θ∂
t
+ ∂
θ
+
i
sin θ
∂
φ
. (8.87)

8.4 Special observers in Kerr space-time 169
We have l ·n = −1, m ·m =0, ¯m · ¯m =0,andm · ¯m = 1. Note that l and k
+
are
aligned; the proportionality factor (r
2
+ a
2
)/Δ makes l geodesic.
8.4 Special observers in Kerr space-time
The Kerr solution is particularly important in astrophysics since it describes the
geometrical environment of a rotating black hole or, in the weak-field limit, that
of a rotating spherical source. Because of its prominent role it is essential to
describe the orbits which can host physically realistic observers.
Static observers
The 4-velocity of a static observer is given by
m =
1
M
∂
t
,m
= −M(dt − M
φ
dφ), (8.88)
where M and M
φ
are respectively the lapse and shift functions defined by
M ≡
√
−g
tt
=
Δ −a
2
sin
2
θ
Σ
,M
φ
= −
g
tφ
g
tt
= −
2Mra sin
2
θ
Δ −a
2
sin
2
θ
. (8.89)
In terms of the lapse and shift functions we have
g = −M
2
(dt − M
φ
dφ) ⊗(dt −M
φ
dφ)+γ
ab
dx
a
⊗ dx
b
, (8.90)
where γ
ab
= g
ab
+ M
2
M
2
φ
δ
φ
a
δ
φ
b
.
Static observers only exist outside the ergosphere, defined by the equation
g
tt
= 0, that is
r = M±
M
2
− a
2
cos
2
θ. (8.91)
A frame adapted to a static observer is the following
e(m)
ˆ
t
= m,
e(m)
ˆr
=
1
√
g
rr
∂
r
=
Δ
Σ
∂
r
,
e(m)
ˆ
θ
=
1
√
g
θθ
∂
θ
=
1
Σ
∂
θ
, (8.92)
e(m)
ˆ
φ
=
1
√
γ
φφ
[ ∂
φ
+ M
φ
∂
t
]
=
1
sin θ
Δ −a
2
sin
2
θ
ΔΣ
∂
φ
−
2aMr sin
2
θ
Δ −a
2
sin
2
θ
∂
t
. (8.93)

170 Observers in physically relevant space-times
The static observers form a congruence of accelerated world lines with accel-
eration vector
a(m)=
M
Σ
3/2
(Δ −a
2
sin
2
θ)
√
Δ(r
2
− a
2
cos
2
θ) e(m)
ˆr
− 2a
2
r sin θ cos θe(m)
ˆ
θ
, (8.94)
and vorticity vector
ω(m)=
M
Σ
3/2
(Δ −a
2
sin
2
θ)
2
√
Δra cos θe(m)
ˆr
+ a sin θ(r
2
− a
2
cos
2
θ) e(m)
ˆ
θ
, (8.95)
while the expansion vanishes identically.
One can now evaluate the transport law for the spatial triad e(m)
ˆa
along the
world line of m.Wehave
P (m)∇
m
e(m)
ˆr
= −ζ
(fw)
ˆ
θ
e(m)
ˆ
φ
,
P (m)∇
m
e(m)
ˆ
θ
= ζ
(fw)
ˆr
e(m)
ˆ
φ
,
P (m)∇
m
e(m)
ˆ
φ
= ζ
(fw)
ˆ
θ
e(m)
ˆr
− ζ
(fw)
ˆr
e(m)
ˆ
θ
, (8.96)
where
ζ
(fw)
ˆr
= −
2aMr
√
Δcosθ
Σ
3/2
(Σ −2Mr)
,
ζ
(fw)
ˆ
θ
= −
aMsin θ(r
2
− a
2
cos
2
θ)
Σ
3/2
(Σ −2Mr)
, (8.97)
are the components of the Fermi-Walker angular velocity vector. On the equato-
rial plane we have ζ
(fw)
ˆr
=0and
ζ
(fw)
ˆ
θ
= −
aM
r
3
(1 −2M/r)
. (8.98)
Note that here, with an abuse of notation, we have denoted ζ
(fw,m,e(m)
ˆa
)
simply
by ζ
(fw)
.
Zero-angular-momentum observers
Observers who have no angular momentum with respect to the flat infinity are
termed ZAMOs, and move on world lines which are orthogonal to the hypersur-
faces t = constant in Boyer-Lindquist coordinates. Their 4-velocity is given by
n
= −Ndt, n =
1
N
(∂
t
− N
φ
∂
φ
), (8.99)

8.4 Special observers in Kerr space-time 171
where N and N
φ
are the corresponding lapse and shift functions
N =
ΔΣ
A
,N
φ
= −
2aMr
A
. (8.100)
In terms of these functions, the space-time metric can be written in the following
form:
g = −N
2
dt ⊗dt + g
ab
(dx
a
+ N
a
dt) ⊗(dx
b
+ N
b
dt), (8.101)
where N
a
= N
φ
δ
a
φ
. ZAMOs exist everywhere outside the outer horizon r
+
.
A tetrad frame adapted to ZAMOs is the following:
e(n)
ˆ
t
= n, e(n)
ˆr
=
Δ
Σ
∂
r
,
e(n)
ˆ
θ
=
1
Σ
∂
θ
,e(n)
ˆ
φ
=
1
sin θ
Σ
A
∂
φ
. (8.102)
The world lines of the ZAMO congruence have an acceleration vector
a(n)=a(n)
ˆr
e
ˆr
+ a(n)
ˆ
θ
e
ˆ
θ
, (8.103)
where
a(n)
ˆr
= −
M
√
ΔΣ
3/2
A
a
2
cos
2
θ[(r
2
+ a
2
)
2
− 4Mr
3
]
−r
2
[(r
2
+ a
2
)
2
− 4a
2
Mr]
,
a(n)
ˆ
θ
= −
2sinθ cos θMra
2
(r
2
+ a
2
)
Σ
3/2
A
; (8.104)
they have a non-zero expansion with expansion tensor
θ(n)=θ(n)
ˆr
ˆ
φ
[e(n)
ˆr
⊗ e(n)
ˆ
φ
+ e(n)
ˆ
φ
⊗ e(n)
ˆr
]
+ θ(n)
ˆ
θ
ˆ
φ
[e(n)
ˆ
θ
⊗ e(n)
ˆ
φ
+ e(n)
ˆ
φ
⊗ e(n)
ˆ
θ
], (8.105)
where
θ(n)
ˆr
ˆ
φ
=
aMsin θ
Σ
3/2
A
(a
4
cos
2
θ − r
2
a
2
cos
2
θ − r
2
a
2
− 3r
4
),
θ(n)
ˆ
θ
ˆ
φ
=
2ra
3
Msin
2
θ cos θ
√
Δ
Σ
3/2
A
, (8.106)
while the vorticity vanishes identically.
One can now evaluate the transport law for the spatial triad e(n)
ˆa
along the
world line of n.Wehave
P (n)∇
n
e(n)
ˆr
= −ζ
(fw)
ˆ
θ
e(n)
ˆ
φ
,
P (n)∇
n
e(n)
ˆ
θ
= ζ
(fw)
ˆr
e(n)
ˆ
φ
,
P (n)∇
n
e(n)
ˆ
φ
= ζ
(fw)
ˆ
θ
e(n)
ˆr
− ζ
(fw)
ˆr
e(n)
ˆ
θ
, (8.107)

172 Observers in physically relevant space-times
where
ζ
(fw)
ˆr
= −
2a
3
Mr
√
Δsin
2
θ cos θ
Σ
3/2
A
= −θ(n)
ˆ
θ
ˆ
φ
, (8.108)
ζ
(fw)
ˆ
θ
=
aMsin θ[a
2
cos
2
θ(a
2
− r
2
) −r
2
(a
2
+3r
2
)])
Σ
3/2
A
= θ(n)
ˆr
ˆ
φ
.
On the equatorial plane we have ζ
(fw)
ˆr
=0and
ζ
(fw)
ˆ
θ
= −
aM(3r
2
+ a
2
)
r
2
(r
3
+ a
2
r +2a
2
M)
. (8.109)
Moreover, the only non-vanishing components of ZAMO kinematical quantities
are a(n)
ˆr
and θ(n)
ˆr
ˆ
φ
. Note that here, with an abuse of notation, we have denoted
ζ
(fw,n,e(n)
ˆa
)
simply by ζ
(fw)
.
Observers on general spatially circular orbits
Consider now a family of spatially circular orbits with unit tangent vector field
U =Γ(∂
t
+ ζ∂
φ
), (8.110)
where Γ > 0 is defined as
Γ=
1 −ζ
2
sin
2
θ(r
2
+ a
2
) −
2Mr
Σ
(1 −aζ sin
2
θ)
2
−1/2
(8.111)
and ζ is constant along U, i.e. £
U
ζ = 0. This class includes static observers with
ζ
(static)
= 0 (8.112)
as well as ZAMOs with
ζ
(ZAMO)
= −N
φ
. (8.113)
One may decompose the vector field U with respect to ZAMOs, obtaining a re-
parameterization of the given family of orbits in terms of the relative velocity or
the rapidity instead of the angular velocity, that is
U = γ[n + ν(U, n)] = γ
n + ||ν(U, n)||e(n)
ˆ
φ
=coshα(U, n) n +sinhα(U, n)e(n)
ˆ
φ
, (8.114)
where γ ≡ γ(U, n)=coshα(U, n) is the Lorentz factor and ν(U, n)=ν(U, n)
ˆ
φ
e
ˆ
φ
.
A useful relation between ζ and ν(U, n)
ˆ
φ
is given by
ν(U, n)
ˆ
φ
=
√
g
φφ
N
(ζ + N
φ
), (8.115)
yielding the following expression for the Lorentz factor:
γ =ΓN. (8.116)
