Davis J.C. Statistics and Data Analysis in Geology (3rd ed.)

Подождите немного. Документ загружается.

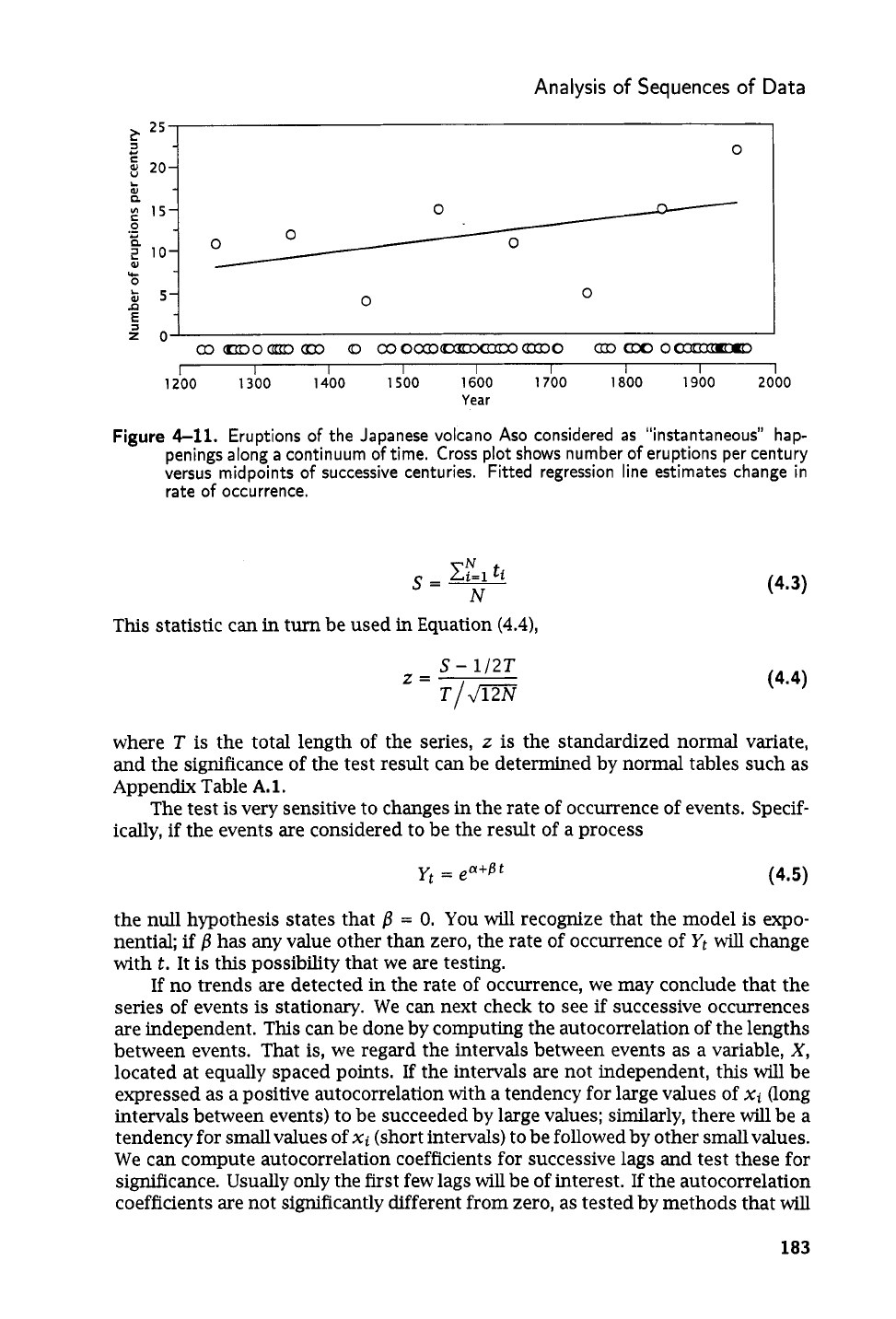
Analysis

Sequences

Data

;

20-

15-

10-

This statistic can in turn be used in Equation

(4.4),

1/2T

T/rn

(4.4)

where

is the total length of the series,

the standardized normal variate,

and the significance of the test result can be determined by normal tables such as

Appendix Table

The test is very sensitive to changes in the rate of occurrence of events. Specif-

ically, if the events

are

considered to be the result of a process

p+Bt

(4.5)

the null hypothesis states that

You will recognize that the model is expo-

nential;

has

any

value other than zero, the rate of occurrence of

will

change

with

It is this possibility that we

are

testing.

no trends are detected in the rate of occurrence, we may conclude that the

series of events is stationary. We can next check to see

successive occurrences

are independent. This can be done by computing the autocorrelation of the lengths

between events. That is, we regard the intervals between events as a variable,

located at equally spaced points.

the intervals

are

not independent, this will be

expressed as a positive autocorrelation with a tendency for large values of

(long

intervals between events) to be succeeded by large values; similarly, there will be a

tendency for small values of

(short intervals) to be followed by other smallvalues.

can

compute autocorrelation coefficients for successive lags and test these for

significance. Usually only the first

few

lags will be of interest.

the autocorrelation

coefficients are not significantly different from zero, as tested by methods that

will

183

Statistics and

Data

Analysis in

Geology

Chapter

be developed later in this chapter, we can conclude that the events are occurring

independently in time or space.

we have established that the series is neither autocorrelated nor contains a

trend, we may wish to test the possibility that the events are distributed accord-

ing to a

Poisson distribution.

You will recall from Chapter

that the Poisson

a discrete probability distribution that

can

be regarded as the limiting case of the

binomial when

the number of trials, becomes very large, and

the probability

of success on

any

one trial, becomes very small. We

can

imagine that our time

series is subdivided into

intervals of equal duration.

events occur randomly,

the number of intervals that contain exactly

2,.

events

will

follow the bi-

nomial distribution.

we make the lengths of the intervals progressively shorter,

becomes progressively larger and the probabilities of occurrence decline. The

binomial distribution becomes difficult to compute, but the Poisson can be readily

used because it does not require either

directly. Instead, the product

all

that is needed, which is given by the

rate

occurrence

of events.

The Poisson probability model assumes that (a) the events occur independently,

(b)

the probability that

event occurs does not change with time, (c) the proba-

bility that an event will occur in an interval is proportional to the length of the

interval, and (d) the probability of more than one event occurring at the same time

is vanishingly small.

The equation for the Poisson distribution in this instance is

p(X)

e-”AX/X!

(4.6)

Note that the rate of occurrence,

is the only parameter of the distribution.

Typ-

ical Poisson frequency distributions are shown

Figure

4-12.

The distribution is

applicable to such problems as the rate that telephone calls come to a switchboard

or the length of time between failures in a computer system. It seems reasonable

that it also may apply to the series of geological events described at the beginning

of this section.

we can determine that our series follows a Poisson distribution,

we can use the characteristics of the distribution to make probabilistic forecasts of

the series.

The Kolmogorov-Smirnov test provides a simple way to test the goodness of fit

of a series of events to that expected from a Poisson distribution. First, the series

must be converted to a cumulative form

where

is the time from the start of the series to the

ith

event, and

is the total

length of the series. Three estimates can then be calculated

The first test

simply the maximum positive difference between the observed se-

ries and that expected from a Poisson, the second

the maximum negative differ-

ence, and the third is the larger of the absolute values of the two. The test statistic,

184

Analysis

Sequences

Data

Figure

4-12.

Poisson probability distributions with difFerent rates

occurrence,

ex-

pressed

numbers

occurrences per interval.

(a)

6.0.

(b)

2.0.

(c)

0.6.

can

be compared to two-tailed critical values given in Appendix Table

A.7.

the statistic exceeds the critical value, the maximum deviation

larger than that

expected

a sample collected at random from a Poisson distribution.

Runs

Tests

The simplest type of sequence is a succession of observations arranged in order of

occurrence, where the observations are two mutually exclusive categories or states.

Consider

rock collector cracking open concretions

a search for fossils. The

breaking of a concretion constitutes a trial, and each trial has

two

mutually exclusive

outcomes: The concretion either contains a fossil or it does not. The sequence of

successes and failures by the collector during the course of a day forms a special

type of time series. We can experimentally create a similar succession by flipping

pennies and noting the occurrence

heads or tails. The sequence generated might

resemble this set of twenty trials:

HTHHTHTTTHTHTHHTTHHH

We intuitively expect, of course, that about ten heads

will

appear, and we can de-

termine the probability of obtaining this (or any other) number of heads. Here we

obtained

heads; assuming the coin

unbiased, the probability of obtaining this

number in

trials

0.16

or about one in

six.

We would expect similar trials to

contain

10,

heads slightly more than one-third

the time. Results of this

experiment follow the binomial distribution, discussed in Chapter

185

Statistics and Data Analysis in Geology

Chapter

One aspect that we have not considered, however, is the order in which the

heads appear.

probably would regard a sequence such as

HHHHHHHHHHHTTTTTTTTT

as being very strange, although the probability of obtaining this

many

heads

trials is the same as

the preceding example. At the other extreme, the regular

alternation of heads and tails

HTHTHTHTHTHTHTHTHTHH

would also appear very unusual to us, although the probability of the number of

heads is unchanged. What arouses our suspicions is not the proportion

heads

but the order in which they appear. We assume that heads and tails

will

occur at

random;

the two preceding examples, it seems

very

unlikely that they have.

We can test these sequences for randomness of occurrence by examining the

number of

runs.

Runs

are defined

uninterrupted sequences

the same state.

The first set of trials contains

runs, the second only

and the third contains

19.

Runs in the first sequence shown are underlined:

(Start)

HTHHTIJTTTHTIJTHTTHHH

1 1

11 12 13

(End)

We can calculate the probability that a given sequence of

runs

was created by

the random occurrence of two states (heads and tails, in this example). This is done

by enumerating all possible ways of arranging

items of state

and

items of

state

The total number of

runs

in a sequence is denoted

tables are available

which give critical values of

for specified

nl,

n2,

and level of significance,

(x.

However,

and

each exceed ten, the distribution of

can

be closely ap-

proximated by a normal distribution, and we can use tables of the standard normal

variate

for our statistical tests. The expected mean number of

runs

a randomly

generated sequence of

items of state

and

items of state

The expected variance in the mean number of

runs

2nln2(2nlnZ

n2)

(n1+

n2I2(n1

CTU

(4.9)

these equations, we can determine the mean number of

runs

and the stan-

dard error of the mean number of

runs

all

possible arrangements of

and

items. Having calculated these,

can create a z-test by Equation

(4.10),

where

is the observed number of

runs:

(4.10)

You

will

recognize that this is simply Equation

(2.37)

rewritten to include the

runs

statistics. We

can

formulate a variety of statistical hypotheses which can be tested

with this statistic.

For

example, we may wish to see if a sequence contains more

186

Analysis

Sequences

Data

than the expected number of

runs

from a random arrangement; the null hypothesis

and alternative are

Hi:

U>U

and too many

runs

leads to rejection. The test is one-tailed. Conversely, we may

wish to determine

the sequence contains an improbably low number of

runs.

The

appropriate alternatives

are

Ho:

Ur8

H1:

u<u

and too few

runs

will

cause rejection of the null hypothesis.

Again,

the test is one-

tailed. We may wish to reject either form of nonrandomness.

two-tailed test

appropriate, with hypotheses

Ho:

U=8

Hi:

Uf8

can

work through the test procedure for the first series of coin flips and

determine the likelihood of achieving this sequence by a random process. The null

hypothesis states that there is no difference between the observed number of

runs

and the mean number of

runs

from random sequences of the same size.

will use

a two-tailed test, and reject

there are too many

too few

runs

the sequence.

Therefore, the proper alternative is

Hi:

UfU

Using a

0.05)

level of significance, our critical regions are bounded by

-1.96

and

+1.96.

first calculate the expected

mean

and standard deviation of

runs

for random sequences having

heads

(nl

11)

and

tails

(n2

9):

9)(2

11)*(9

aiJ

2-(

4.6

The test statistic is

1.0

U-U

13- 10.9

z=-

2.1

The number of

runs

the sequence is one standard deviation from the mean of

all

runs

possible

such a sequence, and does not fall within the critical region.

Therefore, the number of

runs

does not suggest that the sequence is nonrandom.

The other sequences,

contrast, yield very different test results. Because

and

are the same for all three sequences,

and

(TU

also are the same.

For

the second

sequence, the test statistic is

10.9

2.1

-4.2

and for the third,

10.9

3.9

2.1

187

Statistics and Data Analysis in Geology

Chapter

Both of these values lie within the critical region, and we would reject the hypothesis

that they contain the number of

runs

expected in random sequences.

Geologic applications of this test may not be obvious, because we ordinarily

must consider more than two states in a succession. Stratigraphic sections

tra-

verses across thin sections, for example, usually include at least three states and

these cannot be ranked in

meaningful way. We will consider ways that certain se-

quences can be reduced to dichotomous states, but first we will examine a geologic

application of the

runs

test to a traverse through a two-state system.

Simple pegmatites originate by crystallization of the last, volatile-laden sub-

stances squeezed off from solidifying granitic magma. Their textures result from

simultaneous crystallization of quartz and feldspar at the eutectic point.

the

solidifying pegmatite is undisturbed, we might suppose that quartz and feldspar

begin to appear at random locations within the cooling body.

This

situation may

persist, with grains crystallizing at random, until the entire mass is solid. However,

the presence of one crystal, perhaps feldspar, might stimulate the local crystalliza-

tion of additional crystals of feldspar, eventually producing a patchwork texture.

Alternatively, growth of a crystal of one state might locally deplete the magma of

that constituent, retarding crystallization and resulting

a highly alternating mo-

saic of quartz and feldspar.

large slab

polished pegmatite used as a window

ledge in the washroom of a geology building provides a way

for

students to investi-

gate these alternative possibilities. The polished surface allows easy discrimination

of adjacent grains,

a line drawn on the ledge produces a sequence through the

quartz and feldspar grains in the pegmatite.

The line on the polished slab may

be regarded as a random sample of possible successions through the pegmatite

body from which the slab was quarried. The quartz-feldspar sequence along the

line is listed in

Table

4-6.

Our problem is to determine

the alternations between

quartz and feldspar form a random pattern;

there is a systematic tendency for

one state to succeed itself;

whether there is a tendency for one state to imme-

diately succeed the other. Perform a runs test on this data and evaluate the three

possibilities.

Table

4-6.

Sequence

100

feldspar

(F)

and quartz

(Q)

grains encountered

along traverse through pegmatite.

(Start)

F QQF QQFF QF QFFFFFFFQQFQFFF

QFF FFQFFF QQF QFQQQFFFFFQFF

FFF QQQQFFQQQFFFFFF QF QFFFF

FQF QF QFF QFFFFF QFFF QQF QF F

(End)

We will now consider a related statistical procedure for examining what are called

runs

and

runs

down.

are concerned, not with two distinct states, but whether

observation exceeds

is smaller than the preceding observation.

Figure

4-13

shows a typical sequence that can be analyzed by means of a

runs

test.

The segment

abc

is a

run

up, because each observation

larger than the pre-

ceding one; similarly, the segment

ghi

is a

run

down. Segment

cdef

is a

run

down

even though the difference between

and

is zero.

This

is because the interval

lies between segments

and

ef,

both of which

run

downward; therefore, the

188

Analysis

Sequences

Data

Figure 4-13.

Sequence

data points to be analyzed

the method

runs up and down.

entire segment

cdef

can be considered as

single downward

run.

The interval

can

be considered either as part of the run down

ghi

or the

run

ijk,

as the total

number of

runs

remains the same

either case.

this example, we are assuming

that the successive points have integer values.

the observations are expressions

of magnitude, they ordinarily will contain fractional parts, and ties (two successive

points with identical values) are unlikely.

By considering only differences in magnitude between successive points, we

have reduced the data sequence to a string having only two states (or three,

ties

occur). We

can

rewrite the sequence

Figure

4-13

in the following form:

-0-

-o+

Regarding the first zero as

‘I-”

gives a total of five

runs,

three of

“+”

and two of

‘I-”

(it makes no difference

the number of

runs

we call the second zero

“+”

“-”).

We can now apply test procedures outlined for the case of sequences

two

dissimilar items

(Eqs.

4.8-4.10).

We must have a large sample to utilize the normal

approximation method presented here, but

most geologic problems, adequate

numbers of samples will be available.

Table 4-7.

Numbers

radiolarian tests per square centimeter

in thin sections

siliceous shale.

(Bottom

ofsection)

1 2

9 9

12 7

2 2

3 3

491010

912

10 12 14

17 19 14 4 2

0 0

8 14

(Topof

section)

In the study

a silicified shale unit in the Rocky Mountains, it was noted

that the rock contained unusual numbers of well-preserved radiolarian tests. Their

presence

the silicified shale suggested a causal relationship,

a sequence of

samples was collected at approximately equal intervals

exposure through

the unit. Thin sections were made of the samples and the number of radiolarian

tests

10-mm

area of the slides was counted. Data for

samples are

given in

Table

4-7

and shown graphically

Figure 4-14.

Does the abundance of

189

Statistics and Data Analysis in Geology

Chapter

Number

radiolarians

per

cm2

Figure

4-14.

Number

radiolarian

tests

per square centimeter in

thin

sections

siliceous

Mowry Shale.

radiolarians vary at random through the section?

computer program could be

written that will perform the necessary calculations, but the programming effort

probably exceeds the difficulty of computing the test statistic by hand.

In this procedure, observations are dichotomized by comparing their magni-

tudes to the preceding observations. Actually,

runs

tests may be applied to data

dichotomized by

any

arbitrary scheme, provided the hypothesis being tested re-

flects the dichotomizing method. For example, a common test procedure

dichotomize a series by subtracting each observation from the median of

all

obser-

vations, and testing the signs for randomness of

runs

about the median. We also

can test the randomness of

runs

about the mean, and we will use this as a test of

residuals from trends later in this chapter. Runs tests are another example of the

nonparametric procedures introduced in Chapter

There are a number of variants on the runs tests described here. Informa-

tion about these tests may be found in texts on nonparametric statistics, such as

Conover (1999, p. 122-142) and Siege1 and Castellan (1988, section

4.5).

Examples

of the geologic application of runs tests are included in Miller and

Kahn

(1962,

chapter 14) and Rock (1988, topic 16). Some investigators consider the length of

the longest

run

indicator of nonrandomness, and others use the number of

turning points, which are points in the sequence where the signs of successive ob-

servations change. In certain instances these tests may be more appropriate than

the procedures described here. The runs-up-and-down test generally is regarded

as the most powerful of the runs tests because it utilizes changes in magnitude of

every point with respect to adjacent points. Other dichotomizing schemes reflect

only changes with respect to a single value such as the median or mean.

Runs tests are appropriate when the cause of nonrandomness

the object

of investigation. They test for a form of nonrandomness expressed by the pres-

ence of too few or too many runs, and do not identify overall trends. It should be

190

Analysis

Sequences

Data

emphasized that randomness itself cannot be proven, as the condition of random

occurrence is implied in the null hypothesis. Rather, at specified levels of signifi-

cance, we

can

demonstrate that the null hypothesis is incorrect and the sequence is

therefore not random.

can

fail to

reject

the null hypothesis, implying that we

have failed to find

any

indication of nonrandomness. We will next consider proce-

dures for detecting trends,

systematic changes in average value, and will find that

runs tests may be used to good advantage

conjunction with these procedures.

Least-Squares Methods and Regression Analysis

In many types of problems,

are

concerned not only with changes along a se-

quence, but are also interested

where these changes occur. To

examine

these

problems, we must have a collection of measurements of a variable and also must

know the locations of the measurement points. Both the variable and the scale

along the sequence must be expressed

units having magnitude: it is not suffi-

cient simply to know the order of succession of points. We

are

interested in the

general tendency of the data in most of the examples we will now consider.

This

tendency

will

be used to interpolate between data points, extrapolate beyond the

data sequence, infer the presence of trends, or estimate characteristics that

may

interest to the geologist.

certain assumptions can justifiably be made about

the distribution of the populations from which the samples are collected, statistical

tests called

regression analyses

can

be performed.

must be emphasized that

are

now using the expression “sequence”

the broadest possible sense. Regression methods are useful for much more than

the analysis of observations arranged in order

time

space; they can be used

to analyze

any

bivariate data set when it

useful to consider one of the variables

as a function of the other. It is as though one variable forms

scale along which

observations of the other variable are located, and we want to examine the nature

of changes in this variable as we move up or down the scale.

Table

4-8.

Moisture content

core samples

Recent mud in Louisiana estuary.

Moisture (g water/100 g

Depth, ft dried solids)

0.0

5.0

10.0

15.0

20.0

25.0

30.0

35.0

124.0

78.0

54.0

35.0

30.0

21.0

22.0

18.0

The data in

Table

4-8

are the moisture contents of samples from a core through

Recent marine muds accumulating in a small inlet on the

U.S.

Gulf Coast in eastern

Louisiana. These data

are

also in file

LOUISMUD.TXT.

The measurements were made

191

Chapter

Spatial

Analysis

Although geologists study

a three-dimensional world, their view of it is

strongly two dimensional.

This

reflects in part the fact that the third dimension,

depth, often is accessible to only

fraction of the extent of the other two spa-

tial dimensions.

Also,

our

thoughts are conditioned by the media in which we

express them, and maps, photographs, and cross-sections are printed or drawn on

flat sheets

paper. We may be interested in the geologic features exposed

a deep

mine with successive levels, adits, and raises creating a complex three-dimensional

net, yet we must reduce this network to flat projections in order to express

our

ideas concerning the relationships we see.

Geologic Maps, Conventional and Otherwise

Geologists are carefully trained to read, utilize, and create maps; probably no other

group of scientists

as adept at expressing and envisioning dimensional relation-

ships. Maps are compact and efficient means of expressing spatial relationships

and details-they are as important to Earth scientists as the conventions for scales

and notes are to the musician.

In this chapter, we will examine methods for analyzing features on what we

loosely define as “maps”: two-dimensional representations of areas. Usually the

area is geographical (a quadrangle, mining district, country,

etc.)

and the map is

a method for reducing very large-scale spatial relationships

they can be easily

perceived. However, the representation may equally well be a “map” of a thin sec-

tion or electron photomicrograph, where the relationships between features have

been enlarged

they become visible. Maps, in this general definition, include tra-

ditional geologic and topographic maps and also aerial photographs, mine plans,