Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

2.6 Subsequences 53

sinx > 0 if there is an integer k so that 2kπ < x < (2k + 1)π; and sinx < 0 if

there is an integer k so that (2k − 1)π < x < 2kπ. Observe that n increases by

steps of length 1 while the intervals on which sinx takes positive or negative values

has length π ≈ 3.14. Consequently, a

takes the value +1 for three or four terms

in a row, followed by three or four terms taking the value −1.

Consequently, both 1 and −1 are limits of certain subsequences of (a

). To

compute a particular sequence n

for which a

= 1 for all k requires a much

more delicate analysis depending on π. One of the nice things about analysis is

that one can often make signiﬁcant use of such a sequence without knowing the

details of which subsequence is used.

2.6.6. EXAMPLE. Consider the sequence (a

) = (sinn)

∞

n=1

. As the angles n

radians for n ≥ 1 are marked on a circle, they appear gradually to ﬁll in a dense

subset. If this can be demonstrated, we should be able to show that sinθ is a limit

of a subsequence of our sequence for any θ in [0, 2π]. The key is to approximate

the angle 0 modulo 2π by integers.

This can be done using the Pigeonhole Principle. Let m be a positive integer

and ε > 0 be any positive real number. Choose an integer N so large that Nε > 2π.

Divide the circle into N arcs of length 2π/N radians each. Then consider the N +1

points 0, m, 2m, . . . , N m modulo 2π on the circle. Since there are N + 1 points

distributed into only N arcs, at least one of them contains two points, say im and

jm, where i < j. Then n = jm − im represents an angle of at most 2π/N < ε

radians up to a multiple of 2π. That is, n = ψ + 2πs for some integer s and real

number |ψ| < ε. In particular, |sinn| < ε and n ≥ m. Moreover, since π is not

rational, n is not an exact multiple of 2π.

So given θ ∈ [0, 2π], construct a subsequence as follows. Let n

= 1. Recur-

sively we construct an increasing sequence n

such that

|sinn

− sinθ| <

Once n

is deﬁned, take ε =

k+1

and m = n

+ 1 in the previous paragraph. This

provides an integer n > n

such that n = ψ + 2πs and |ψ| <

k+1

. Thus there is a

positive integer t such that |θ − tψ| <

k+1

. Therefore

(2.6.7) |sin(tn) − sin(θ)| = |sin(tψ) − sin(θ)| < |tψ − θ| <

k + 1

Set n

k+1

= tn. This completes the induction. The result is a subsequence such that

lim

k→∞

sin(n

) = sin θ.

To verify equation (2.6.7), we could use the Mean Value Theorem or we can

use trig identities. See the Exercises for the latter, more computational argument. If

f(x) = sinx, then f

(x) = cos x. So by the Mean Value Theorem (Theorem 6.2.4),

there is a point ξ between tψ and θ such that

sin(tψ) − sin(θ)

tψ − θ

cosξ

≤ 1.

54 The Real Numbers

Rearranging yields |sin(tψ) − sin(θ)| < |tψ − θ|.

Therefore, we have shown that every value in the interval [−1, 1] is the limit of

some subsequence of the sequence (sinn)

∞

n=1

2.6.8. EXAMPLE. Consider the sequence b

= 3 and b

n+1

= (b

+ 8/b

)/2.

Notice that

n+1

− 8 =

+ 16 + (64/b

) − 32

− 16 + (64/b

)

− 8/b

)

− 8)

It follows that b

> 8 for all n ≥ 2, and b

− 8 = 1 > 0 also. Thus

0 < b

n+1

− 8 <

− 8)

Iterating this, we obtain b

− 8 < 32

−1

, b

− 8 < 32

−3

and b

− 8 < 32

−7

. In

general, we establish by induction that

0 < b

− 8 < 32

1−2

n−1

Since b

is positive and b

− 8 = (b −

√

8)(b +

√

8), it follows that

0 < b

−

√

8 =

− 8

√

1−2

n−1

√

< 6(32

−2

n−1

Lastly, using the fact that 32

= 1024 > 10

, we obtain

0 < b

−

√

8 < 10 · 10

−3·2

n−2

In particular, lim

n→∞

√

8. In fact, the convergence is so rapid that b

approx-

imates

√

8 to more than 750 digits of accuracy. See Example 11.2.2 for a more

general analysis using Newton’s method.

Now let a

= 8/b

. Then a

is monotone increasing to

√

8. Both a

and b

are

rational numbers. Thus the sets J

= {x ∈ Q : a

≤ x ≤ b

} form a decreasing

sequence of nonempty intervals of rational numbers with empty intersection.

Exercises for Section 2.6

A. Show that (a

) =

n cos

(n)

√

+2n

∞

n=1

has a convergent subsequence.

B. Does the sequence (b

) =

n + cos(nπ)

√

+ 1

∞

n=1

have a convergent subse-

quence?

2.7 Cauchy Sequences 55

C. Does the sequence (a

) =

coslog n

∞

n=1

converge?

D. Show that every sequence has a monotone subsequence.

E. Use trig identities to show that |sin x − siny| ≤ |x − y|.

HINT: Let a = (x + y)/2 and b = (x −y)/2. Use the addition formula for sin(a ±b).

F. Deﬁne x

= 2 and x

n+1

+ 5/x

) for n ≥ 1.

(a) Find a formula for x

n+1

− 5 in terms of x

− 5.

(b) Hence evaluate lim

n→∞

(d) Show that the tenth term approximates the limit to over 600 decimal places.

G. Let (x

)

∞

n=1

be a sequence of real numbers. Suppose that there is a real number L so

that L = lim

n→∞

3n−1

= lim

n→∞

3n+1

= lim

n→∞

. Show that lim

n→∞

exists and equals

H. Let (x

)

∞

n=1

be a sequence of real numbers. Suppose that there is a real number L with

the property that every subsequence (x

)

∞

k=1

has a subsubsequence

k(l)

∞

l=1

with

lim

l→∞

k(l)

= L. Show that the whole sequence converges to L.

HINT: If it were false, you could ﬁnd a subsequence bounded away from L.

I. Suppose that (x

)

∞

n=1

is a sequence of real numbers. Also suppose that L

are real

numbers with lim

k→∞

= L. If for each k ≥ 1, there is a subsequence of (x

)

∞

n=1

converging to L

, show that some subsequence converges to L.

HINT: Find an increasing sequence n

so that |x

− L| < 1/k.

J. Suppose that (x

)

∞

n=1

is a sequence of real numbers.

(a) If L = liminfx

, show that there is a subsequence (x

)

∞

k=1

so that lim

k→∞

= L.

(b) Similarly, prove that there is a subsequence (x

)

∞

l=1

so that lim

l→∞

= limsupx

K. Let (x

)

∞

n=1

be an arbitrary sequence of real numbers. Prove that there is a subse-

quence (x

)

∞

k=1

so that either lim

k→∞

= ∞ or lim

k→∞

= −∞, or there is a real

number L so that lim

k→∞

= L.

L. Construct a sequence (x

)

∞

n=1

so that for every real number L, there is a subsequence

)

∞

k=1

with lim

k→∞

= L.

2.7. Cauchy Sequences

Can we decide if a sequence converges without ﬁnding the potential limit

value? We are looking for an intrinsic property of a sequence that is equivalent

to convergence and that doesn’t use any information about the limit. This leads

us to the notion of a space being complete if all sequences that are “supposed” to

converge actually do. As we shall see, this completeness property has been built

into the real numbers by our construction of all inﬁnite decimals.

56 The Real Numbers

To obtain an appropriate condition, notice that if a sequence (a

) converges to

L, then as well as getting close to the limit, the terms of the sequence are getting

close to each other. To be precise,

2.7.1. PROPOSITION. Let (a

)

∞

n=1

be a sequence converging to a limit L. Then

for every ε > 0, there is an integer N such that

− a

| < ε for all m, n ≥ N.

PROOF. Fix ε > 0 and use the value ε/2 in the deﬁnition of limit. It follows that

there is an integer N so that

− L| <

for all n ≥ N.

Thus if m, n ≥ N , we obtain

− a

| ≤ |a

− L| + |L − a

| <

= ε.

We make the conclusion of this proposition into a deﬁnition.

2.7.2. DEFINITION. A sequence (a

)

∞

n=1

of real numbers is called a Cauchy

sequence provided that for every ε > 0, there is an integer N so that

− a

| < ε for all m, n ≥ N.

This deﬁnition retains the ﬂavour of the deﬁnition of a limit, in that it has the

same logical structure: For all ε > 0, there is an integer N .... However, it does

not require the use of a potential limit L. This permits the following deﬁnition.

2.7.3. DEFINITION. A subset S of R is said to be complete if every Cauchy

sequence (a

) in S (that is, a

∈ S) converges to a point in S.

This brings us to an important conclusion about the real numbers themselves.

2.7.4. COMPLETENESS THEOREM.

A sequence of real numbers converges if and only if it is a Cauchy sequence. In

particular, R is complete.

PROOF. Proposition 2.7.1 shows that convergent sequences are Cauchy.

Conversely, suppose that (a

)

∞

n=1

is a Cauchy sequence. First we show that the

set {a

: n ≥ 1} is bounded. The proof is basically the same as Proposition 2.4.2.

Indeed, take ε = 1 and ﬁnd N sufﬁciently large that

− a

| < 1 for all n ≥ N.

It follows that the sequence is bounded by

max{|a

|, |a

|, . . . , |a

N−1

|, |a

| + 1}.

2.7 Cauchy Sequences 57

By the Bolzano–Weierstrass Theorem 2.6.4, this sequence has a convergent

subsequence, say

lim

k→∞

= L.

Now let ε > 0. From the deﬁnition of Cauchy sequence for ε/2, there is an integer

N so that

− a

| <

for all m, n ≥ N.

And from the deﬁnition of limit using ε/2, there is an integer K so that

− L| <

for all k ≥ K.

Pick any k ≥ K such that n

≥ N. Then for every n ≥ N,

− L| ≤ |a

− a

| + |a

− L| <

= ε.

So lim

n→∞

= L. ¥

2.7.5. REMARK. This theorem is not true for the rational numbers. Here is

an example of a Cauchy sequence of rational numbers that does not converge to a

rational number. Deﬁne the sequence (a

)

∞

n=1

= 1.4, a

= 1.41, a

= 1.414, a

= 1.4142, a

= 1.41421, . . .

and in general, a

is the ﬁrst n + 1 digits in the decimal expansion of

√

2. If n and

m are greater than N, then a

and a

agree for at least ﬁrst N + 1 digits. Thus

− a

| < 10

−N

for all m, n ≥ N.

This shows that (a

)

∞

n=1

is a Cauchy sequence. (Why?)

However, this sequence has no limit in the rationals. In our terminology, Q

is not complete. Of course, this sequence does converge to a real number, namely

√

2. This is the essential difference between R and Q: The set of real numbers is

complete and Q is not.

2.7.6. EXAMPLE. Let α be an arbitrary real number. Deﬁne a

= [nα]/n,

where [x] is the nearest integer to x. Then

[nα] − nα

≤ 1/2. So

− α| =

[nα] − nα

≤

Therefore, lim

n→∞

= α. Indeed, given ε > 0, choose N so large that

< ε. Then

for n ≥ N , |a

− α| < ε/2. Moreover if m, n ≥ N,

− a

| ≤ |a

− α| + |α − a

| <

= ε.

Thus this sequence is Cauchy.

58 The Real Numbers

2.7.7. EXAMPLE. Consider the inﬁnite continued fraction

2 +

2 + ···

Does this make any sense? It has to be interpreted as the limit of the ﬁnite fractions

2 +

··· .

This formulation of the sequence is not very useful, so we should look for a better

way of deﬁning the general term. In this case, there is a recursion formula for

obtaining one term from the preceding one:

, a

n+1

2 + a

for n ≥ 1.

In order to establish convergence, we will show that (a

) is Cauchy. Consider

the difference

n+1

− a

n+2

2 + a

−

2 + a

n+1

− a

(2 + a

)(2 + a

n+1

)

Now a

> 0 and it is readily shown that a

> 0 for all n ≥ 2 by induction. Hence

the denominator (2 + a

)(2 + a

n+1

) > 4. So we obtain

n+1

− a

n+2

| <

− a

n+1

for all n ≥ 1.

Since |a

− a

| = 1/10, we may iterate this inequality to estimate

− a

| <

10 · 4

− a

| <

10 · 4

− a

| <

10 · 4

− a

n+1

| <

10 · 4

n−1

−n

The general formula estimating the difference may be veriﬁed by induction.

Now it is straightforward to estimate the difference between arbitrary terms a

and

2.7 Cauchy Sequences 59

for m < n:

− a

| =

− a

m+1

) + (a

m+1

− a

m+2

) + ··· + (a

n−1

− a

)

≤ |a

− a

m+1

| + |a

m+1

− a

m+2

| + ··· + |a

n−1

− a

−m

+ 4

−m−1

+ ··· + 4

1−n

)

2 · 4

−m

5(1 −

)

−m

< 4

−m

This tells us that our sequence is Cauchy. Indeed, if ε > 0, choose N so large that

−N

< ε. Then for all m, n ≥ N,

− a

| < 4

−m

≤ 4

−N

< ε.

Thus by our Completeness Theorem (Theorem 2.7.4), it follows that (a

)

∞

n=1

converges; say, lim

n→∞

= L. To calculate L, use the recursion relation

L = lim

n→∞

= lim

n→∞

n+1

= lim

n→∞

2 + a

2 + L

It follows that L

+ 2L − 1 = 0. Solving yields L = ±

√

2 − 1. Since L > 0, we

see that L =

√

2 − 1.

Exercises for Section 2.7

A. Give an example of a sequence (a

) such that lim

n→∞

−a

n+1

| = 0, but the sequence

does not converge.

B. Let (a

) be a sequence with the property that lim

N→∞

n=1

− a

n+1

| < ∞. Show that

) is Cauchy.

C. Show that if (x

)

∞

n=1

is a Cauchy sequence, then it has a subsequence (x

) such that

lim

K→∞

k=1

− x

k+1

| < ∞.

D. Suppose that (a

) is a sequence such that a

≤ a

2n+2

≤ a

2n+3

≤ a

2n+1

for all n ≥ 0.

Show that this sequence is Cauchy if and only if lim

n→∞

− a

n+1

| = 0.

E. Give an example of a sequence (a

) such that a

≤ a

2n+2

≤ a

2n+3

≤ a

2n+1

for all

n ≥ 0 that does not converge.

F. Let a

= 0 and set a

n+1

= cos(a

) for n ≥ 0.

(a) Try this on your calculator. (Remember to use radians mode.)

(b) Show that a

≤ a

2n+2

≤ a

2n+3

≤ a

2n+1

for all n ≥ 0.

n+2

− a

n+1

| ≤ r|a

− a

n+1

| for all n ≥ 0. Hence show that this sequence is

Cauchy.

(d) Describe the limit geometrically as the intersection point of two curves.

60 The Real Numbers

G. Evaluate the continued fraction (Example 2.7.7)

1 +

1 + ···

H. Let x

= 0 and x

n+1

√

5 − 2x

for n ≥ 0. Show that this sequence converges and

compute the limit.

HINT: Show that the even terms increase and the odd terms decrease to the same limit.

I. Consider an inﬁnite binary expansion (0.e

. . . )

base 2

, where each e

∈ {0, 1} and

this expansion is deﬁned to be the real number that is the limit of the sequence a

i=1

−i

when the limit exists. Prove that for every choice of zeros and ones, this

sequence is Cauchy and therefore deﬁnes a unique real number.

J. We can develop a construction of the real numbers from the rational numbers using

Cauchy sequences. This exercise presents the deﬁnitions that go into such a proof.

(a) Associate a “point” to each Cauchy sequence of rational numbers. Find a way to

decide when two Cauchy sequences should determine the same point without using

limits. HINT: Combine the two sequences into one.

(b) Your deﬁnition in (a) should be an equivalence relation. Is it? (See Appendix 1.6.)

(d) How is order deﬁned?

2.8. Appendix: Cardinality

Cardinality is the notion that measures the size of a set in the crudest of ways—

by counting the numbers of elements. Obviously, the number of elements in a set

could be 0, 1, 2, 3, 4, or some other ﬁnite number. Or a set can have inﬁnitely many

elements. Perhaps surprisingly, not all inﬁnite sets have the same cardinality. For

our purposes, inﬁnite sets have two possible sizes: countable and uncountable (the

uncountable ones are larger). In this section, the most important ideas to understand

are what countable means and what distinguishes countable sets from those with

larger cardinality. We include a few more sophisticated arguments for enrichment

purposes.

2.8.1. DEFINITION. Two sets A and B have the same cardinality if there is a

bijection f from A onto B. We write |A| = |B| in this case. Similarly, we say that

the cardinality of A is less than that of B (|A| ≤ |B|) if there is an injection f from

A into B.

The deﬁnition says simply that if all of the elements of A can be paired, one-

to-one, with all of the elements of B, then A and B have the same size. If A ﬁts

2.8 Appendix: Cardinality 61

inside B in a one-to-one manner, then A is smaller than B. One of the subtleties

that we address later is whether |A| ≤ |B| and |B| ≤ |A| mean that |A| = |B|. The

answer is yes, but this is not obvious for inﬁnite sets.

2.8.2. EXAMPLES.

(1) The cardinality of any ﬁnite set is the number of elements, and this number

belongs to N

= {0, 1, 2, 3, 4, . . . }. Set theorists go to some trouble to deﬁne the

natural numbers too. But we will take for granted that the reader is familiar with

the notion of a ﬁnite set.

(2) Most sets encountered in analysis are inﬁnite, meaning that they are not ﬁnite.

The sets of natural numbers N, integers Z, rational numbers Q, and real numbers

R are all inﬁnite. Moreover, we have the natural containments N ⊂ Z ⊂ Q ⊂ R.

So |N| ≤ |Z| ≤ |Q| ≤ |R|. Notice that the integers can be written as a list

0, 1, −1, 2, −2, 3, −3, . . . . This amounts to deﬁning a bijection f : N → Z by

f(n) =

(

(1 − n)/2 if n is odd

n/2 if n is even.

Therefore, |N| = |Z|.

2.8.3. DEFINITION. A set A is a countable set is it is ﬁnite or if |A| = |N|. The

cardinal |N| is also denoted by ℵ

. This is the ﬁrst letter of the Hebrew alphabet,

aleph, with subscript zero. It is pronounced aleph nought.

An inﬁnite set that is not countable is called an uncountable set.

Notice that two uncountable sets could have different cardinalities. We refer

the reader interested in the possible cardinalities of uncountable sets to [1].

Equivalently, A is countable if the elements of A may be listedas a

, a

, . . . .

Indeed, the list itself determines a bijection from N to A by f(k) = a

. It is a basic

fact that countable sets are the smallest inﬁnite sets.

2.8.4. LEMMA. Every inﬁnite subset of N is countable. Moreover, if A is an

inﬁnite set such that |A| ≤ |N|, then |A| = |N|.

PROOF. Any nonempty subset X of N has a smallest element. Indeed, as X

is nonempty, it contains an integer n. Consider the elements of the ﬁnite set

{1, 2, . . . , n}in order and pick the ﬁrst one that belongs to X—that is, the smallest.

Let B be an inﬁnite subset of N. List the elements of B in increasing order as

< b

< . . . . This is done by choosing the smallest element b

, then the

smallest of the remaining set B \ {b

}, then the smallest of B \ {b

, b

} and so on.

The result is an inﬁnite list of elements of B in increasing order. It must include

every element b ∈ B because {n ∈ B : n ≤ b} is ﬁnite, containing say k elements.

Then b

= b. As noted before the proof, this implies that |B| = |N|.

62 The Real Numbers

Now consider a set A with |A| ≤ |N|. By deﬁnition, there is a injection f of

A into N. Let B = f(A). Note that f is a bijection of A onto B. Then B is an

inﬁnite subset of N. So |A| = |B| = |N|. ¥

2.8.5. PROPOSITION. The countable union of countable sets is countable.

PROOF. By the previous lemma, we may assume that there is a countably inﬁnite

collection of sets A

, A

, . . . that are each countably inﬁnite. Write the ele-

ments of A

as a list a

i,1

, a

i,2

, a

i,3

, . . . . Then we may write A =

i≥1

as a list

as follows:

1,1

, a

1,2

, a

2,1

, a

1,3

, a

2,2

, a

3,1

, a

1,4

, a

2,3

, a

3,2

, a

4,1

, . . . ,

where the elements a

i,j

are written so that i + j is monotone increasing, and within

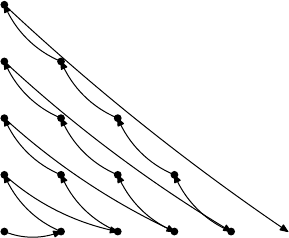
the set of pairs (i, j) with i + j = n, the terms are written with the i’s in increasing

order. See Figure 2.5. Thus A is countable. ¥

1,1

2,1

3,1

4,1

5,1

1,2

1,3

1,4

1,5

FIGURE 2.5. The set N × N is countable.

2.8.6. COROLLARY. The set Q of rational numbers is countable.

PROOF. The set Z × N = {(i, j) : i ∈ Z, j ∈ N} is the disjoint union of the

sets A

= {(i, j) : j ∈ N} for i ∈ Z. Each A

is evidently countable. By

Example 2.8.2(2), Z is countable. Hence Z ×N is the countable union of countable

sets, and hence is countable by Proposition 2.8.5.

Deﬁne a map from Q into Z ×N by f(r) = (a, b) if r = a/b, where a and b are

integers with no common factor and b > 0. These conditions uniquely determine

the pair (a, b) for each rational r, and so f is a function. Clearly, f is injective

since r is recovered from (a, b) by division. Therefore, f is an injection of Q into

a countable set. Hence Q is an inﬁnite set with |Q| ≤ |N|. So Q is countable by

Lemma 2.8.4. ¥