Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

2.1 An Overview of the Real Numbers 33

numbers, it becomes crucial that there are enough real numbers to include the limits

of all convergent sequences of real numbers. Implicit in this statement is some

method for determining whether a sequence is supposed to convergewithout having

to name the limit point.

Since the notion of inﬁnite decimal expansions is taught from a very early

stage, we will take this as our deﬁnition of the real numbers. A subtle point of

our deﬁnition is that an inﬁnite decimal expansion is just an object and does not

imply the need to sum an inﬁnite series. We do not want to use the notion of limit

to deﬁne the real numbers. In the next section, we outline how to deﬁne inﬁnite

decimals precisely and how to order, add, and multiply them. After that is done,

we can safely deﬁne the notion of limit, using the order and arithmetical properties

of real numbers.

Our construction of the real numbers appears to be strongly dependent on the

choice of 10 as the base. For this reason, purists prefer a base independent method

of deﬁning the real numbers, albeit a more abstract one. We are left with the nag-

ging question of whether the number line we construct depends on the number of

digits on our hands. Fortunately, this is not the case but proving it requires consid-

erably more work than we wish to do at present. Our main goal is to get on with

the study of analysis. There is a proof much later in the book, in Example 9.5.6,

that our construction does not depend on the choice of 10 as the base.

As was implied previously, inﬁnite decimals are not the only way to deﬁne

the real numbers. To satisfy the curious, we now sketch one of the base indepen-

dent deﬁnitions of the real numbers. At end of this chapter, we show some of the

ingredients needed for yet another deﬁnition of the real numbers, in Exercise 2.7.J.

In 1858, Dedekind described a formal construction of the real numbers that did

not require the use of any base nor any notion of limit at all. He noticed that for

each real number x, there was an associated set S

= {r ∈ Q : r < x} of rational

numbers. This determines a different set of rational numbers for each real x. Of

course, we deﬁned these sets using the real numbers. But we can turn it around.

Dedekind considered all sets S of rational numbers that have the properties

(1) S is a nonempty subset of Q that is bounded above,

(2) S does not contain its upper bound, and

(3) if s ∈ S and r < s for r ∈ Q, then r ∈ S.

These sets are known as Dedekind cuts. He then associated a point x to each of

these sets. In particular, each rational number r is associated to the set S

described

previously. We can then go on to deﬁne order by inclusion of sets, arithmetic oper-

ations, and limits. This somewhat artiﬁcial construction ﬁnally freed the deﬁnition

of R from reliance on intuitive notions and put analysis on a ﬁrm footing at last.

Exercises for Section 2.1

A. Using Dedekind’s notion of the real numbers, show that addition of two Dedekind cuts

can be deﬁned easily by S + T = {s + t : s ∈ S, t ∈ T }. Verify that S + T is a

Dedekind cut.

B. Deﬁne −S, ST and 1/S, in terms of Dedekind cuts S and T .

34 The Real Numbers

2.2. Inﬁnite Decimals

As discussed in the previous section, we will deﬁne a real number by using an

inﬁnite decimal expansion such as

= 0.33333333333333333333333333333333333333333333333333 . . .

= 0.25000000000000000000000000000000000000000000000000 . . .

√

3 = 1.73205080756887729352744634150587236694280525381038 . . .

π = 3.141592653589793238462643383279502884197169399375105 . . .

e = 2.718281828459045235360287471352662497757247093699959 . . .

and, in general,

x = a

··· .

To be formal, an inﬁnite decimal expansion is a function, say x, from the set

{0, 1, 2, . . .} to the integers Z. We require that for all n ≥ 1, x(n) is in the set

{0, 1, 2, 3, 4, 5, 6, 7, 8, 9}. The point is that this function in no way depends on the

concept of a limit. Of course, it doesn’t seem related to our intuitive picture of the

real line, either.

To relate inﬁnite decimal expansions to the real line, start with a line and mark

two points on the line; and call the left-hand one 0 and the right-hand one 1. Then

we can easily construct points for every integer Z, equally spaced along the line.

Now divide each interval from an integer n to n + 1 into 10 equal pieces, marking

the cuts as n.1, n.2, ..., n.9. Proceed in this way, cutting each interval of length

−k

into 10 equal intervals of length 10

−k−1

and mark the endpoints by the cor-

responding number with k + 1 decimals. In this way, all ﬁnite decimals are placed

on the line.

It seems clear that for every inﬁnite decimal expansion x = a

. . .,

there will be a point on this line called a real number x with the property that

for each positive integer k, x lies in the interval between the two decimal numbers

y = a

. . . a

and y + 10

−k

. For example,

(2.2.1) 3.141592653589 ≤ π ≤ 3.141592653590.

In other words, the decimal expansion of x up to the kth decimal approximates x

to an accuracy of at least 10

−k

. We also have, implicitly, the notion of convergence

of these ﬁnite decimal approximants, which will allow us to make sense of limits

of real numbers.

The astute reader will be aware that there is a problem with this as a deﬁ-

nition of the real numbers. What is the relationship between the numbers 1 and

z = 0.9999999999999. . .? Clearly these are different inﬁnite decimal expansions.

However, for each positive integer k, we have

1 − 10

−k

= 0. 99999999999999

{z }

≤ z ≤ 1.

2.2 Inﬁnite Decimals 35

Thus the difference between this number z and 1 is arbitrarily small. It would create

quite a nonintuitive line if these were allowed to represent different points. To ﬁt in

with our intuition, we must agree that z = 1. That means that some real numbers

(precisely all those numbers with a ﬁnite decimal expansion) have two different

expansions, one ending in an inﬁnite string of zeros, and the other ending with an

inﬁnite string of nines. For example, 0.125 = 0.12499999. . . . If you have read

Section 1.6, you will recognize this as an equivalence relation (see Exercise 1.6.B).

The set of all real numbers is denoted by R. Technically, this is the set of

all inﬁnite decimal numbers with the identiﬁcations described in the previous para-

graph. This achieves a deﬁnition of a large set of points that, on the surface, appears

to make sense and to be adequate for our purposes.

The rational numbers are distinguished among all real numbers by the fact that

their decimal expansions are eventually periodic. See Theorems 1.5.1 and 1.5.3 in

Chapter 1 if this is unfamiliar. What we need to do next is to extend the operations

on Q to all of R. However, there are many details to check. We will not carry out

all of these necessary veriﬁcations, but we will at least outline what needs to be

done.

First, we have a built-in order on the line given by the placement of the points.

This extends the natural order on the ﬁnite decimals. Notice that between any

two distinct ﬁnite decimal numbers, there are (inﬁnitely many) other ﬁnite decimal

numbers. Now if x and y are distinct real numbers given by inﬁnite decimal expan-

sions, these expansions will differ at some ﬁnite point. This enables us to ﬁnd ﬁnite

decimals in between them. Because we know how to compare an inﬁnite decimal

expansion to its ﬁnite decimal approximants [using equations such as (2.2.1)], we

can determine which of x or y is larger.

Second, we must extend the arithmetic properties of the rational numbers to all

real numbers—namely addition, multiplication, and their inverse operations—and

verify all the ﬁeld axioms. This is done by making all the operations consistent

with the order. For example, if x and y are real numbers and k is a positive integer,

then we have the ﬁnite decimal approximants

a = a

. . . a

≤ x ≤ a + 10

−k

and b = b

. . . b

≤ y ≤ b + 10

−k

and so

a + b ≤ x + y ≤ a + b + 2 ·10

−k

Clearly this determines the sum x + y to an accuracy of 2 ·10

−k

for each k. In this

way, the sum is “determined” for all real numbers.

The computation of the sum of two inﬁnite decimals is subtle and cannot be

done exactly by a computer program. The reason is that the ﬁrst digit of x + y may

not be determined exactly after any ﬁxed ﬁnite number of steps, even though the

sum can be known to any desired accuracy. To see why this is the case, consider

x = 0.

nines

}| {

999999. . . 999999

repetitions

}| {

0123456789. . . 012345678931415. . .

y = 0. 999999 . . . 999999

{z }

nines

9876543210. . . 9876543210

{z }

repetitions

a9066. . . .

36 The Real Numbers

When we add x + y using the ﬁrst k decimal digits for any k ≤ 10

, we obtain

k−1 nines

}| {

999999. . . 9999998 ≤ x + y ≤ 2.

k zeros

}| {

000000. . . 000000.

If we take k = 10

, we have computed x + y to an accuracy of 2 · 10

−10

and

still we cannot say for sure whether the ﬁrst digit of the sum is 1 or 2. When we

proceed with the computation using one more digit, we obtain

−1 nines

}| {

999999. . . 99999989 ≤ x + y ≤ 1.

−1 nines

}| {

999999. . . 99999991.

All of a sudden, not only is the ﬁrst digit certainly a 1, but the next 10

− 1 digits

are all nines.

A new period of uncertainty now occurs, again because of the problem that a

long string of nines can roll over to a string of zeros like the odometer in a car.

After using another 10

digits, we obtain a different result depending on whether

a ≤ 4, a = 5 or 6, or a ≥ 7. When a = 4, we get

−1 nines

}| {

9999. . . 99998

nines

}| {

9999. . . 99997 ≤ x + y ≤ 1.

−1 nines

}| {

9999. . . 99998

nines

}| {

9999. . . 99999.

So the digits are now determined for another 10

+ 1 places. When a = 7, we

obtain

−1 nines

z }| {

9999. . . 99999

zeros

z }| {

000. . . 00000 ≤ x + y ≤ 1.

−1 nines

z }| {

9999. . . 99999

zeros

z }| {

000. . . 00002.

Again, the next 10

+ 1 digits are now determined. However, when a = 5, these

digits of the sum are still ambiguous:

−1 nines

z }| {

9999. . . 99998

nines

z }| {

9999. . . 99998 ≤ x + y ≤ 1.

−1 nines

z }| {

9999. . . 99999

zeros

z }| {

000. . . 00000.

The 10

-th decimal digit is still not known.

The important thing to recognize is that these difﬁculties are not a serious im-

pediment to deﬁning the real numbers as inﬁnite decimals. In theory, we know that

the digits in the sum are eventually resolved. It may be true that no matter how

large k is, looking at the ﬁrst k digits of x and y does not tell us if the ﬁrst digit of

x + y is a 1 or a 2. But then we must have, for all k, 2−10

−k

≤ x + y ≤ 2. So we

end up with two possible answers, one ending in an inﬁnite string of nines and the

other with an inﬁnite string of zeros. Since we identify these two expansions as the

same real number, this settles the ﬁrst digit of x + y (and, in fact, all of them).

In real life, knowing the sum to, say, within 2 · 10

−15

is much the same as

knowing it to 15 decimal places (in fact marginally better). So we are content, on

both theoretical and practical grounds, that we have an acceptable working model

of addition.

The issues are similar for the other arithmetic operations: multiplication, ad-

ditive inverses, and multiplicative inverses. It is crucial that these operations are

consistent with order, as this means that they are also continuous (respect limits).

Carrying out all the details of this program is tedious but not especially difﬁcult.

2.3 Limits 37

The key points of this section are that we can deﬁne real numbers as inﬁnite

decimal expansions (with some identiﬁcations) and can rigorously deﬁne all the

ﬁeld operations; the result ﬁts our intuitive picture of the real line. Moreover, we

have the order, distance, and arithmetic properties that we expect. Once we have

developed the notion of limit in the next two sections, we will use inﬁnite decimal

expansions in Section 2.5 to prove the Least Upper Bound Principle (2.5.3). This

principle says, in effect, that the real number system has no gaps, resolving the

problems discussed in the last section and giving us a solid foundation for the rest

of our work.

Exercises for Section 2.2

A. If x 6= y, explain an algorithm to decide if x < y or y < x. Does your method break

down if x = 0.9999. . . and y = 1.0000. . . ?

B. If a < b and x < y, is ax < by? What additional order hypotheses make the conclu-

sion correct?

C. Deﬁne |x| = max{x, −x}.

(a) Prove that |xy| = |x||y| and |x

−1

| = |x|

−1

(b) Prove the triangle inequality |x + y| ≤ |x| + |y|.

HINT: Consider x and y of the same sign and different signs as separate cases.

D. Prove by induction that |x

+ x

+ ··· + x

| ≤ |x

| + |x

| + ··· + |x

E. Prove that

|x| − |y|

≤ |x − y|.

F. (a) Prove that if x < y, then there is a rational number r with a ﬁnite decimal expansion

such that x < r < y.

(b) Prove that if x < y, then there is an irrational number z such that x < z < y.

HINT: Use (a) and add a small multiple of

√

2 to r.

G. Suppose that r 6= 0 is a rational number and that x is irrational. Show that r + x and

rx are irrational.

H. If m and n are integers, show that

√

3 −

≥

HINT: Rationalize the numerator and use the irrationality of

√

2.3. Limits

The notion of a limit is the basic notion of analysis. Limits are the culmination

of an inﬁnite process; and it is the concern with limits in particular that separates

analysis from algebra. In this section, we will deal with limits of a sequence of real

numbers. Later we will concern ourselves with limits of functions, possibly with

values in other spaces.

In the 1680s, Newton and Leibniz independently developed calculus. But it is

not calculus as we know it today. Their writings about limits were vague and de-

pended on physical reasoning that was somewhat circular and certainly was impre-

cise. In the late eighteenth century, some mathematicians, such as d’Alembert, saw

38 The Real Numbers

the need to developa precise notion of limit, while other great mathematicians, such

as Lagrange, tried to develop calculus without dependence on this notion. Gauss in

1812 was the ﬁrst mathematician to concern himself with tests for convergence of

inﬁnite series as necessary before attempting to evaluate the limit. It was not until

1829 that Cauchy gave a deﬁnition of limit that is close to the modern one we use

today.

Intuitively, to say that a sequence a

converges to a limit L means that eventu-

ally all the terms of the (tail of the) sequence approximate the limit value L to any

desired accuracy. To make this precise, we introduce a subtle deﬁnition.

2.3.1. DEFINITION. A real number L is the limitof a sequence of real numbers

)

∞

n=1

if for every ε > 0, there is an integer N = N(ε) > 0 so that

− L| < ε for all n ≥ N.

We say that the sequence (a

)

∞

n=1

converges to L, and we write lim

n→∞

= L.

The important issue in this deﬁnition is that, from some point on, every element

of the sequence approximates the limit L to any desired accuracy. A little thought

shows that we could consider only values for ε of the form

−k

. The statement

−L| <

−k

means that a

and L agree to k decimal places. Thus a sequence

converges to L precisely when eventually all the terms of the sequence agree with

L to k decimals of accuracy for every k, no matter how large.

2.3.2. EXAMPLE. Consider the sequence (a

) = (n/(n + 1))

∞

n=1

, which we

claim converges to 1. If the deﬁnition agrees with our intuitive idea of convergence,

we should be able to pick N for any ε. Suppose ε = .05. We need to ﬁnd some N

so that

n + 1

− 1

< .05 for all n ≥ N.

First we simplify the left-hand side of this equation:

n+1

− 1

n+1

. If n ≥ 20,

then

n + 1

− 1

n + 1

≤

< .05.

So it is enough to choose N = 20.

We could also choose N = 73. It is not necessary to ﬁnd the best choice for

N. However, as we shall see in connection with the analysis of numerical methods,

better estimates can lead to better algorithms for computation.

If ε =

−k

, what should we choose for N? Arguing as before, we see that if

n ≥ 2 · 10

, then

n + 1

− 1

n + 1

≤

2 · 10

+ 1

−k

So we can choose N = 2 ·10

2.3 Limits 39

2.3.3. EXAMPLE. Consider a

2n−1

= π +

and a

= π for n ≥ 1. This

sequence converges to π. Indeed, given ε > 0, choose a large positive integer N

so that

< ε. Then if n > 2N , we may write n = 2k − 1 or n = 2k for some

k > N. In the ﬁrst case,

− π| = |a

2k−1

− π| =

< ε,

while in the second case,

− π| = |a

− π| = 0 < ε.

Note that some terms of a convergent sequence may actually equal the limit exactly.

2.3.4. EXAMPLE. Consider the sequence (a

) = ((−1)

)

∞

n=1

. Since this ﬂips

back and forth between two values that are far apart, it evidently does not converge

in any intuitive sense. To show this using our deﬁnition, we need to show that the

deﬁnition of limit fails for any choice of L. However, for this L, we need ﬁnd only

one value of ε that violates the deﬁnition.

Consider the fact that

− a

n+1

| = |(−1)

− (−1)

n+1

| = 2

for all n, no matter how large. So let L be any real number. We notice that L

cannot be close to both 1 and −1. To turn this into a quantitative statement that

avoids cases, we use a trick. For any real number L,

− L| + |a

n+1

− L| ≥ |(a

− L) − (a

n+1

− L)| = |a

− a

n+1

| = 2.

Thus

max{|a

− L|, |a

n+1

− L|} ≥ 1.

So now take ε = 1. If this sequence did converge, there would be an integer

N so that |a

− L| < 1 for all n ≥ N. But this is not true for both N and N + 1.

Consequently, this sequence does not converge.

2.3.5. EXAMPLE. Consider the sequence

sinn

∞

n=1

. The numerator oscil-

lates wildly, but it remains bounded between ±1 while the denominator goes off to

inﬁnity. We obtain the estimates

−

≤

sinn

≤

We know that lim

n→∞

= 0 = lim

n→∞

−

as this is exactly like Example 2.3.2.

Therefore, the limit can be computed using a familiar principle from calculus:

2.3.6. THE SQUEEZE THEOREM.

Suppose that three sequences (a

), (b

) and (c

) satisfy

≤ b

≤ c

for all n ≥ 1 and lim

n→∞

= lim

n→∞

= L.

Then lim

n→∞

= L.

40 The Real Numbers

PROOF. Let ε > 0. There is some N

so that

− L| < ε for all n ≥ N

or equivalently, L −ε < a

< L + ε for all n ≥ N

. There is also some N

so that

− L| < ε for all n ≥ N

or L − ε < c

< L + ε for all n ≥ N

. Then, if n ≥ max{N

, N

}, we have

L − ε < a

≤ b

≤ c

< L + ε.

Thus |b

− L| < ε for n ≥ max{N

, N

}, as required. ¥

Returning to our example

sinn

∞

n=1

, we have

lim

n→∞

= lim

n→∞

−1

= 0.

By the Squeeze Theorem,

lim

n→∞

sinn

= 0.

2.3.7. EXAMPLE. A more sophisticated example comes from calculus. Con-

sider the sequence

n sin

¢¢

∞

n=1

. To apply the Squeeze Theorem, we need to

obtain an estimate for sinθ when the angle θ is small. Consider a sector of the

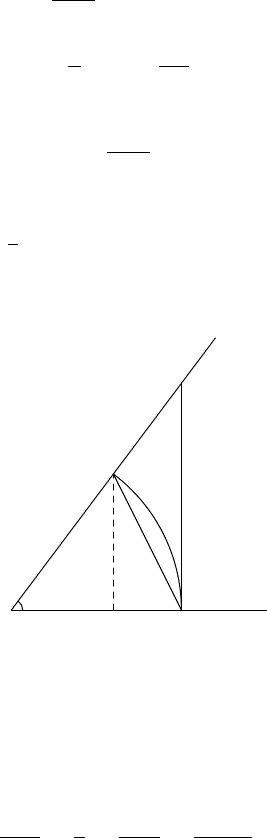
circle of radius 1 with angle θ and the two triangles, as shown in Figure 2.1.

FIGURE 2.1. Sector OAB between 4OAB and 4OAC.

Since

4OAB ⊂ sector OAB ⊂ 4OAC,

we have the same relationship for their areas:

sinθ

tanθ

sinθ

2cosθ

2.3 Limits 41

A manipulation of these inequalities yields

cosθ <

sinθ

< 1.

In particular, cos

< n sin

< 1. Moreover,

cos

1 − sin

1 −

> 1 −

However,

lim

n→∞

1 −

= 1 = lim

n→∞

Therefore, by the Squeeze Theorem, lim

n→∞

n sin

= 1.

Exercises for Section 2.3

A. In each of the following, compute the limit. Then, using ε = 10

−6

, ﬁnd an integer N

that satisﬁes the limit deﬁnition.

(a) lim

n→∞

sinn

√

(b) lim

n→∞

cos

n→∞

loglog n

(d) lim

n→∞

(e) lim

n→∞

+ 2n + 1

− n + 2

(f) lim

n→∞

√

+ n − n

B. Prove from the deﬁnition that the sequence a

= L for n ≥ 1 has a limit.

C. Show that lim

n→∞

sin

nπ

does not exist using the deﬁnition of limit.

D. Prove that if a

≤ b

for n ≥ 1, L = lim

n→∞

and M = lim

n→∞

, then L ≤ M.

E. Prove that if L = lim

n→∞

, then L = lim

n→∞

and L = lim

n→∞

F. Sometimes, a limit is deﬁned informally as follows: “As n goes to inﬁnity, a

gets

closer and closer to L.” Find as many faults with this deﬁnition as you can.

(a) Can a sequence satisfy this deﬁnition and still fail to converge?

(b) Can a sequence converge yet fail to satisfy this deﬁnition?

G. Deﬁne a sequence (a

)

∞

n=1

so that lim

n→∞

exists but lim

n→∞

does not exist.

H. Suppose that lim

n→∞

= L and L 6= 0. Prove that a

6= 0 with only ﬁnitely many

exceptions.

I. Let a

and a

be positive real numbers, and set a

n+2

√

n+1

√

for n ≥ 0.

(a) Show that a

≥ 1 for n sufﬁciently large. (That is, there is some N so that this

holds for all n ≥ N.)

(b) Let ε

= |a

− 4|. Show that ε

n+2

≤ (ε

n+1

+ ε

)/3 for n ≥ N.

J. For each real number x, determine if the sequence

1 + x

∞

n=1

has a limit, and

compute it when it exists.

K. Show that the sequence (logn)

∞

n=1

does not converge.

42 The Real Numbers

L. Provide an example of sequences with a

≤ b

≤ c

such that both L = lim

n→∞

and

M = lim

n→∞

exist, but lim

n→∞

does not exist.

2.4. Basic Properties of Limits

We have already developed a number of basic properties of limits in the ex-

amples and exercises of the previous section. For example, the Squeeze Theorem

and Exercise 2.3.D show that limits respect order. Another simple but important

observation is that convergent sequences are bounded.

2.4.1. DEFINITION. A set A ⊂ R is bounded above if there is a real number

M so that a ≤ M for all a ∈ A. Similarly, the set A is bounded below if there is

a real number m such that a ≥ m for all a ∈ A. A set that is bounded above and

below is called bounded. Equivalently, A is bounded if there is one real number B

so that |a| ≤ B for all a ∈ A.

2.4.2. PROPOSITION. If (a

)

∞

n=1

is a convergent sequence of real numbers,

then the set {a

: n ∈ N} is bounded.

PROOF. Let L = lim

n→∞

. If we set ε = 1, then by the deﬁnition of limit, there is

some N > 0 so that |a

− L| < 1 for all n ≥ N. In other words,

L − 1 < a

< L + 1 for all n ≥ N.

Let

M = max{a

, a

, . . . , a

N−1

, L + 1}

and

m = min{a

, a

, . . . , a

N−1

, L − 1}.

Clearly, for all n, we have m ≤ a

≤ M . ¥

Note that there is no special reason to use 1 in this proof except convenience.

We could have picked ε = 1/2 or ε = 42 and the argument would still work.

It is also crucial that the arithmetic operations respect limits. Proving this is

straightforward. For completeness, here are the details.

2.4.3. THEOREM. If lim

n→∞

= L, lim

n→∞

= M and α ∈ R, then

(1) lim

n→∞

+ b

= L + M,

(2) lim

n→∞

αa

= αL,

(3) lim

n→∞

= LM, and

(4) lim

n→∞

if M 6= 0.