Daniels M.J., Hogan J.W. Missing Data in Longitudinal Studies: Strategies for Bayesian Modeling and Sensitivity Analysis

Подождите немного. Документ загружается.

240 CASE STUDIES: NONIGNORABLE MISSINGNESS

Speciﬁcation and calibration of MNAR priors

There are two obstacles that must be overcome in specifying MNAR priors:

the high dimension of theparameter space for ∆,andtheneed to make a

speciﬁc choice of prior distribution. Even if a series of point mass priors will

be used to conduct a sensitivity analysis, we must specify the range of values

to include.

We focus on departures from MAR in terms of the intercept sensitivity

parameters (∆

(1:2)

, ∆

(1:3)

, ∆

(2:3)

), reducing the number of sensitivity param-

eters to six (three for each treatment group). The justiﬁcation for this choice

is based mainly on interpretability; each represents a diﬀerence in the condi-

tional mean of Y

given previous Y ’s between patterns. For example,

∆

(1:2)

= E(Y

| Y

,S =1)− E(Y

| Y

,S ≥ 2)

represents the diﬀerence in E(Y

| Y

)between those with missing and ob-

served Y

.Similarly,

∆

(1:3)

= E(Y

| Y

,S =1)− E(Y

| Y

,S =3),

∆

(2:3)

= E(Y

| Y

,S =2)− E(Y

| Y

,S =3).

As a ﬁnal constraint, we assume ∆

(1:3)

=∆

(2:3)

,anddenote the common

parameter by ∆

(•:3)

.Theimplication of our ﬁnal constraint is that, relative

to MAR, the diﬀerence in E(Y

| Y

)between those with observed and

missing Y

is common across missing data patterns S =1andS =2.Hence

the reduced set of ∆ parameters for sensitivity analysis and incorporation of

informative priors is denoted by

∆ =(∆

(1:2)

, ∆

(•:3)

). (10.8)

There are four sensitivity parameters inall: one set foreachtreatment group.

Recall that the treatment eﬀect of interest is

θ = E(Y

| Z =1)− E(Y

| Z =0),

with θ>0ifquadstrengthonEGisgreater than on EP. With respect to

summarizing posterior inference about θ under MNAR, each of our analyses

below has two components: First,weexaminesensitivity to departures from

MAR in terms of posterior mean and posterior probabilities for treatment

eﬀect over a set of values ∆ ∈ D .Asensitivity analysis summarizing the

range of posterior inferences about mean treatment eﬀect over a range of

missing data mechanisms is carried out by summarizing the posterior mean

E(θ | y

obs

, z, ∆)and posterior probability P(θ>0 | y

obs

, z, ∆)overall∆ ∈

D.InAnalysis1wegive ranges forthesequantities over D,andinAnalysis 2

we use contour plots to identify subsets of D where inference about treatment

eﬀect might diﬀer substantially from MAR. Second,weuseinformative priors

GROWTH HORMONE STUDY 241

for ∆ to generate an overall inference about θ.Inourcase,weassume∆ is

uniformly distributed over a domain D .

In general, components of ∆ can range over the entire real line. It is there-

fore necessary to calibrate or otherwise bound its domain D.Thedirection of

departure from MAR can typically be informed by context. In our analyses be-

low, we assume dropouts have lower mean quad strength than non-dropouts.

In terms of the model, our assumption is that for j =2, 3, the conditional

mean of quad strength Y

given the past is lower for those with missing Y

compared to those with observed Y

The scale of departure from MAR can be determined in any number of

ways. Our approach is to use the variability in the observed data. Because

the components of ∆ in (10.8) correspond to intercepts in the conditional

distributions p

≥2

| y

)andp

| y

), a natural metric for scaling D

is the set of residual variances for identiﬁed conditional distributions in the

pattern mixture model (10.1). For example, by setting D = D(τ ), where

D(τ )=

−

(≥2)

, 0

−

(3)

, 0

departures from MAR are assumed to lie within one standard deviation for

the conditional distributions p

≥2

| y

)andp

| y

Priors for ∆ can be calibrated in the same fashion. Following with this

example, we can assume p(∆ | ξ

)=p(∆ | τ ), and set

∆ | τ

(≥2)

,τ

(3)

∼ Unif{D (τ )}.

In our analyses, we approximate this approach by plugging in posterior means

for relevant components of τ to determine D .Details are provided below.

Analysis 1: Assume common ∆ between treatments

Sensitivity analyses and informative priors used in the ﬁrst analysis will be

based on the two-dimensional parameter ∆ =(∆

(1:2)

, ∆

(•:3)

) ∈ D

.Wesetthe

maximum range of departures from MAR roughly equal to the highest residual

standard deviation between the treatment-speciﬁc regressions for p(y

| y

)

and p(y

| y

)basedon the observed data. Using the results in Table 10.2,

where the residual standard deviation ranges from 14 to 23 for the regression

| Y

)andfrom8.9to15for(Y

| Y

), we set D

=[−20, 0] × [−15, 0].

To help with interpretation, it is useful to understand the eﬀect of depar-

tures from MAR on the marginal means µ

= E(Y

)andµ

= E(Y

). For

clarity we again suppress treatment indices. Consider ﬁrst µ

;inthepattern

mixture model,

= E(Y

)



s=1

E(Y

| S = s). (10.9)

242 CASE STUDIES: NONIGNORABLE MISSINGNESS

Table 10.2 Growth hormone trial: posterior mean (posterior SD) of regression pa-

rameters for pattern mixture model (10.1) ﬁt under MAR constraints.

Treatment Group

Model Covariate Parameter EP(z =0) EG(z =1)

| Y

Int. α

(≥2)

23 (6.9) 14 (15)

(≥2)

.89 (.10) .97 (.19)

(≥2)

14 23

| Y

Int. β

(3)

11 (5.5) –5.3 (12)

(3)

.21 (.13) .45 (.19)

(3)

.59 (.12) .65 (.14)

(3)

8.9 15

In this summation, E(Y

| S =1)isnotidentiﬁed and is therefore a function

of sensitivity parameters; speciﬁcally,

E(Y

| S =1) = E

|S=1

{E(Y

| Y

,S =1)}

= E(α

(1)

+ α

(1)

| S =1)

= α

(1)

+ α

(1)

=(α

(≥2)

+∆

(1:2)

)+(α

(≥2)

+∆

(1:2)

)µ

(1)

Recall that we have constrained ∆

(1:2)

=0,sothat

E(Y

| S =1)=α

(≥2)

+∆

(1:2)

+ α

(≥2)

(1)

Referring back to (10.9), write E(Y

)=µ

= µ

(∆

(1:2)

)toemphasize its

dependence on the sensitivity parameter. The eﬀect of departures from MAR

on µ

is captured by the diﬀerence

(∆

(1:2)

) − µ

(0) = φ

∆

(1:2)

. (10.10)

Hence the contribution of the sensitivity parameter to the shift in µ

is pro-

portional to the fraction dropping out at S =1.

As with E(Y

), the marginal mean E(Y

)istheweighted average

= E(Y

)



s=1

E(Y

| S = s).

GROWTH HORMONE STUDY 243

Because neither E(Y

| S =1)norE(Y

| S =2)isidentiﬁed,µ

depends on

both sensitivity parameters; hence we write µ

= µ

(∆

(1:2)

, ∆

(•:3)

Calculations similar to those above can be used to show that

(∆

(1:2)

, ∆

(•:3)

) − µ

(0, 0) = (φ

+ φ

)∆

(•:3)

+ φ

(3)

∆

(1:2)

. (10.11)

Expressions (10.10) and (10.11) can be used in conjunction with output from

Table 10.2 to understand the maximum eﬀect of departures from MAR, based

on the set D

.Atthe boundary value (∆

(1:2

, ∆

(•:3)

)=(−20, −15), we see that

for z =0(EP),

(−20) − µ

(0) =

(−20)

= −3.5,

(−20, −15) − µ

(0, 0) = (

)(−15) +

(.59)(−20)

= −6.6, (10.12)

and for z =1(EG),

(−20) − µ

(0) =

(−20)

= −6.3,

(−20, −15) − µ

(0, 0) = (

)(−15) +

(.65)(−20)

= −10.4. (10.13)

Hence departures from MAR may lead to mean quadstrengththatisupto

6.6 units lower for EP and 10.4 units lower for EG, relative to MAR.

When the sensitivity parameters are equivalent by treatment group, as they

arehere, the dropout proportion inﬂuences which treatment group will have

greater sensitivity to departures from MAR. Because dropout rate is higher

on the EG arm, the gradient for µ

away from MAR is steeper than for µ

;

the posterior mean of µ

ranges from 78 to 68; and for µ

,therange is 73

to 68. Posterior treatment eﬀect over D

ranges from 5to1,withassociated

posteriors for P(θ>0) taking values from .74 to .56. None of the posteriors

over thesetD

leads to the conclusion that mean quad strength on EG is

greater than on EP.

If prior belief about the values for ∆ is conﬁned to the fact that it falls

within D ,andifeach∆ ∈ D

is assumed to have equal aprioriprobability,

then we can assign a uniform prior over D

and summarize treatment eﬀects

using a single posterior distribution. Results from this approach are summa-

rized in Table 10.1 under MNAR-1. As expected, posterior marginal means

have shifted downward. Uncertainty about ∆ is reﬂected in the increased

posterior SD for parameters that rely on ∆ (means at months 6, 12), but

importantly, not for fully identiﬁed parameters (means at month 0). Posterior

mean treatment diﬀerence is 3.1 (PSD=8.2), which is closer to zero but

does not change the qualitative conclusion under MAR that quad strength on

244 CASE STUDIES: NONIGNORABLE MISSINGNESS

the EG arm is similar to EP. Given the sensitivity analysis above, this is not

surprising.

Analysis 2: Assume ∆ is treatment speciﬁc

In the previous analysis, we assumed a common ∆ across the treatment arms.

However, it may be more reasonable toassume that the degree of departure

from MAR diﬀers on the twoarms.Recall that our previous analysis was

based on the sensitivity parameters

∆

(1:2)

= E(Y

| Y

,S =1)− E(Y

| S ≥ 2)

∆

(•:3)

= E(Y

| Y

,S =2)− E(Y

| Y

,S =3)

= E(Y

| Y

,S =1)− E(Y

| Y

,S =3).

In this analysis, we allow these parameters to vary by treatment, but to keep

the dimension of ∆ equal to 2, we combine them by assuming

∆

(1:2)

(z)

=∆

(•:3)

(z)

=∆

for z =0, 1.

It is again helpful to quantify the eﬀect of ∆

on the shift in marginal

means; arguing as before, it is straightforward to show that the maximum

eﬀects of departures from MAR on the marginal means µ

= E(Y

| Z = z)

and µ

= E(Y

| Z = z)are

(∆

) − µ

(0) = ∆

(∆

) − µ

(0) = ∆

{φ

+ φ

(1 + β

(3)

)}.

We set D

=[0, 20] × [0, 20], based on the largest residual standard deviation

over both treatments in Table 10.2.

Using calculations similar to (10.12) and (10.13), the following maximum

shifts in µ

and µ

relative to MAR are

(−20) − µ

(0) = −3.5

(−20) − µ

(0) = −6.3

z =0(EP)

(−20) − µ

(0) = −6.6

(−20) − µ

(0) = −12.5

z =1(EG).

Figure 10.1 shows contours of the posterior mean of θ and of P(θ>0),

conditional on ﬁxed values of (∆

, ∆

) ∈ D

.ThecontourplotofP(θ>0)

indicates the speciﬁc departures from MAR that would change the qualitative

conclusions about treatment eﬀect. In particular, the part of the posterior

distribution having P (θ>0) >.9isintheregion where ∆

is near zero and

∆

is between −20 and − 15; i.e., where dropouts on EG are roughly MAR,

GROWTH HORMONE STUDY 245

but dropouts on EP have quad strength much lower than expected relative

to MAR.

As with Analysis 1, we can use an informative prior on ∆.For illustration

we use a uniform prior on D

=[−20, 0]×[−20, 0]; the posterior is summarized

in Table 10.1. The results largely agree with Analysis 1, but posterior variances

are higher because of the wider range for ∆.

Posterior predictive model checking

Although the distributions p(y

mis

| y

obs

,s)andp(y

obs

,s)arefully separated,

we have made a number of parametric and distributional assumptions about

p(y

obs

,s); primarily, we have assumed multivariate normality and linearity

of associations. Unlike assumptions about p(y

mis

| y

obs

,s), those applied to

p(y

obs

,s)canbecritiqued. We use Pearson’s χ

statistic (3.19) to assess ﬁt of

the identiﬁed distributions distributions in (10.1) to the observed data using

the posterior predictive approach described in Chapter 8.

Speciﬁcally, to assess the ﬁt of p(y

), we compute

; ω)=



i=1

(ω),

where

(ω)=

− E(Y

| ω)}

var(Y

| ω)

with

E(Y

| ω)=



s=1

(s)

var(Y

| ω)=E{var(Y

| S, ω)} +var{E(Y

| S, ω)}



s=1

[σ

(s)

+ {µ

(s)

− E(Y

| ω)}

To assess the ﬁt of p(y

| y

,S ≥ 2) and p(y

| y

,S =3),weuseT

(y; ω)

and T

(y; ω), respectively, where, for j =2, 3,

(y; ω)=

≥j



i=1

(ω).

As above,

(ω)=

− E(Y

| y

,...,y

i,j−1

,S ≥ j, ω)}

(ω)

246 CASE STUDIES: NONIGNORABLE MISSINGNESS

where

E(Y

| y

,...,y

i,j−1

,S ≥ j, ω)=



s=j

E(Y

| y

,...,y

i,j−1

,S = s)



s=j

(j)

j−1



l=1

(j)

and

(ω)=var(Y

| y

,...,y

j−1

,S ≥ j, ω)=τ

(≥j)

We normalize the data summary T

(y; ω)usingn

≥j

,thetotal number of

subjects in patterns greater than or equal to j.Thereason for doing this is

that the total number in these patterns in the replicated dataset will vary with

each sample from the posterior predictive distribution and will diﬀer from the

observed number of subjects in those patterns in the original dataset.

Posterior predictive probabilities based on T

(·; ω)werecomputed as de-

scribed in Chapter 8. The probabilities for these three checks were .71, .56,

and .56, indicating no evidence of wide departures from the observed data

model.

10.2.9 Summary of pattern mixture analysis

Our strategy here has been to construct the full-data distribution as a PMM.

The general model allows missingness to be MNAR, with MAR as a special

case. The degree of departure from MAR is quantiﬁed by a set of parame-

ters ∆ measuring departures from MAR. The ∆ parameters are completely

nonidentiﬁed, so the ﬁt of the model to observed data is identical across the

assumed missing data mechanisms. We assess the ﬁt of the observed data

model using posterior predictive checks.

Several key issues must be addressed when implementing a PMM analysis.

First, the general model has a large number of sensitivity parameters. In

practical settings, the dimension must be reduced; we have given suggestions

for doing this.

Second, analyses based on examining conditional posteriors at ﬁxed values

of ∆ over a predetermined range D can be useful, but speciﬁcation of D is

subjective. Our approach has been to calibrate D using relevant posterior dis-

tributions under the MAR constraint. Other approaches are certainly possible

and will depend on context. It is important to ensure that choices for D do

not extrapolate the missing data outside of a ‘reasonable’ range (e.g., negative

values of quadriceps strength).

Third, it must be kept in mind that the contour plots generated for Anal-

yses 1 and 2 represent conditional posteriors (or posteriors over an inﬁnite

number of pointmasspriors), and that ideally, a ﬁnal inference should be

GROWTH HORMONE STUDY 247

E(θ|∆

, ∆

)

∆

−20 −15 −10 −5 0

MAR

P(θ>0|∆

, ∆

)

∆

−20 −15 −10 −5 0

MAR

Figure 10.1 Growth hormone trial: contours of posterior mean treatment eﬀect θ

(diﬀerence in quad strength) and of posterior probability P (θ>0) as function of ∆

from Analysis 2.

248 CASE STUDIES: NONIGNORABLE MISSINGNESS

based on a well-motivated prior distribution for the nonidentiﬁed sensitivity

parameters. The priors for ∆ | ξ

used in Analyses 1 and 2 are informed solely

by the choice of D ,andallpossible values in D are weighted equally in our

example here. In practice, however, it is likely that more information is known

about departures from MAR, whether from previous studies or from expert

opinion. In the case study presentation given in Section 10.3, we illustrate the

use of informative priors based on elicited expert opinion.

10.3 OASIS Study: Selection models, mixture models, and elicited

priors

10.3.1 Overview

The OASIS trial is described in detail in Section 1.6. OASIS was a two-arm

randomized trial designed to reduce smoking rates in alcoholics. Smoking sta-

tus was assessed at 1, 3, 6, and 12 months following randomization. For each in-

dividual, the full data comprise the 4×1responsevector of smoking outcomes

Y =(Y

)

,obtainedatmonths1,3,6,and12following baseline;

the corresponding vector of response indicators R =(R

)

;and

treatment group Z (1 if randomized to enhanced intervention, 0 if standard

intervention).

The objective is to compare smoking rates at month 12 between those

randomized to Z =1vs.Z =0.Inference is made in terms of the odds ratio

ϕ =

odds(Y

=1| Z =1)

odds(Y

=1| Z =0)

This trial has intermittent missingness; follow-up time S = S(R)isdeﬁned

as the last time point at which data are observed (all individuals are observed

at the ﬁrst time point):

S =











1ifR =(1, 0, 0, 0)

2ifR =(1, 1, 0, 0)

3ifR ∈{(1, 1, 1, 0), (1, 0, 1, 0)}

4ifR ∈{(1, 1, 1, 1), (1, 0, 1, 1), (1, 1, 0, 1), (1, 0, 0, 1)}.

To handle intermittent missing values, we assume missingness is MAR condi-

tionally on S;thatis,we assume

p(y

mis

| y

obs

,s,z,r)=f(y

mis

| y

obs

,s,z),

or that Y

mis

is independent of R given (Y

obs

,S,Z).

Figure 10.2 displays the smoking rate by pattern from observed data. For

both treatment arms, those who complete the study (S =4)showlowersmok-

ing rates than dropouts. Furthermore, for S ∈{2, 3},smokingrateappears to

increase preceding dropout in ET arm. Later, for the pattern mixture analy-

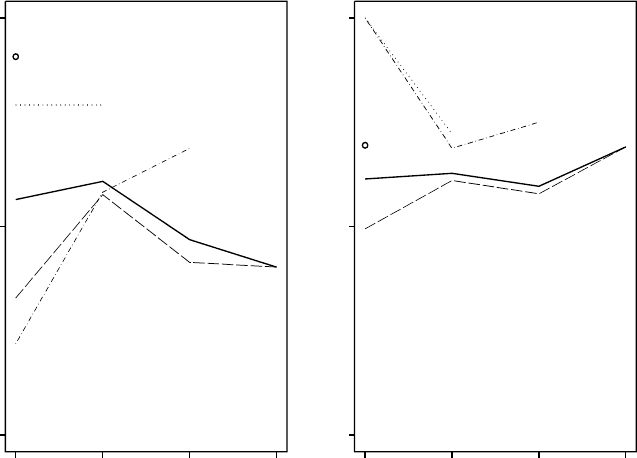
OASIS STUDY 249

sis, we combine the relatively few subjects with S =2orS =3intoasingle

pattern that, using a slight abuse of notation, is labeled as S =(2, 3).

We conduct several analyses using (parametric) selection models and using

mixture models. For the latter, we describe the construction of an informative

prior that will be used for inference under MNAR.

Measurement time j

1234

0.6 0.8 1.0

S=1 (54)

S=2 (12)

S=3 (16)

S=4 (67)

All

Enhanced Intervention

Measurement time j

1234

0.6 0.8 1.0

S=1 (41)

S=2 (9)

S=3 (10)

S=4 (89)

All

Standard Intervention

Figure 10.2 OASIS study: proportion smoking by dropout pattern S at each month,

stratiﬁed by treatment arm (number of subjects per pattern in parentheses).

10.3.2 Selection model speciﬁcation

Aselection model factorization of the full-data model follows p(y | ω) p(r |

y, ω). We use a parametric selection model to infer treatment eﬀect under

both MAR and MNAR. The selection model being used here isparametric

because, we impose constraints on the full-data distribution, and on the miss-

ing data mechanism (similar to the constraints used in Example 8.2). We focus