Dake L.P. Fundamentals of reservoir engineering

Подождите немного. Документ загружается.

SOME BASIC CONCEPTS IN RESERVOIR ENGINEERING 40

the aim should be to operate at above dew point pressure until dry gas breakthrough

occurs in the producing wells. After this, the injection is terminated, and the remaining

dry gas produced.

The dry gas material balance equations can also be applied to gas condensate

reservoirs if the single phase Z−factor is replaced by the, so-called, two phase Z−factor.

This must be experimentally determined in the laboratory by performing a constant

volume depletion experiment.

A volume of gas, G scf, is charged to a PVT cell at an initial pressure p

, which is above

the dew point, and at reservoir temperature. The pressure is reduced in stages as gas

is withdrawn from the cell, and measured as

′

scf, without altering either the cell

volume or the temperature. This simulates the production of the reservoir under

volumetric depletion conditions and therefore, applying the depletion type material

balance equation, (1.35), and solving explicitly for Z gives

2 phase

−

æö

−

ç÷

èø

(1.46)

Until the pressure has dropped to the dew point, the Z−factor measured in this

experiment is identical with the Z−factor obtained using the technique described in

sec. 1.5(a). Below the dew point, however, the two techniques will produce different

results.

The latter experiment, for determining the single phase Z−factor, implicitly assumes

that a volume of reservoir fluids, below dew point pressure, is produced in its entirety to

the surface. In the constant volume depletion experiment, however, allowance is made

for the fact that some of the fluid remains behind in the reservoir as liquid condensate,

this volume being also recorded as a function of pressure during the experiment. As a

result, if a gas condensate sample is analysed using both experimental techniques, the

two phase Z−factor determined during the constant volume depletion will be lower than

the single phase Z−factor. This is because the retrograde liquid condensate is not

included in the cumulative gas production

′

in equ. (1.46), which is therefore lower

than it would be assuming that all fluids are produced to the surface, as in the single

phase experiment.

Figure 1.15(b) shows a typical phase diagram for oil. As already noted, because oil

contains a higher proportion of the heavier members of the paraffin series, the two

phase envelope is more horizontally inclined than for gas.

If the initial temperature and pressure are such that the reservoir oil is at point A in the

diagram, there will only be one phase in the reservoir namely, liquid oil containing

dissolved gas. Reducing the pressure isothermally will eventually bring the oil to the

bubble point, B. Thereafter, further reduction in pressure will produce a two phase

system in the reservoir; the liquid oil, containing an amount of dissolved gas which is

commensurate with the pressure, and a volume of liberated gas. Unfortunately, when

liquid oil and gas are subjected to the same pressure differential in the reservoir, the

SOME BASIC CONCEPTS IN RESERVOIR ENGINEERING 41

gas, being more mobile, will travel with a much greater velocity than the oil. This leads

to a certain degree of chaos in the reservoir and greatly complicates the description of

fluid flow.

From this point of view, it is preferable to produce the reservoir close to (or above)

bubble point pressure, which greatly simplifies the mathematical description. Not only

that, but as will be shown in Chapter 3, operating in such a manner enhances the oil

recovery. The manner in which the reservoir pressure can be maintained at or above

bubble point is conventionally by water injection, a detailed description of which is

presented in Chapter 10.

REFERENCES

1) Lynch, E.J.,1964. Formation Evaluation. Harper and Row, New York.

2) Bradley, J.S., 1975. Abnormal Formation Pressure. The American Ass. of Pet.

Geologists Bulletin, Vol. 59, No. 6, June: 957−973.

3) Chapman, R.E., 1973. Petroleum Geology, a Concise Study. Elsevier Scientific

Publishing Co., Amsterdam: 67−76.

4) Earlougher, R.C., Jr., 1977. Advances in Well Test Analysis. SPE Monograph:

Chapter 8.

5) Lebourg, M., Field, R.Q. and Doh, C.A., 1957. A Method of Formation Testing on

Logging Cable. Trans. AIME, 210: 260−267.

6) Schultz, A.L., Bell, W.T. and Urbanosky, H.J., 1974. Advancements in

Uncased−Hole Wireline−Formation−Tester Techniques. SPE paper 5053,

prepared for the Annual Fall Meeting of the SPE of AIME; Houston, Texas.

October.

7) Craft, B.C. and Hawkins, M.F., Jr., 1959. Applied Petroleum Reservoir

Engineering. Prentice−Hall, Inc. New Jersey.

8) Amyx, J.W., Bass, D.M. and Whiting, R. L., 1960. Petroleum Reservoir

Engineering − Physical Properties. McGraw-Hill.

9) Walstrom, J.E., Mueller, T.D. and McFarlane, R.C., 1967. Evaluating Uncertainty

in Engineering Calculations. J.Pet. Tech., July: 1595−1603.

10) Northern, I.G., 1967. Risk Probability and Decision-Making in Oil and Gas

Development Operations. Paper presented at Petroleum Soc. of CIM. Technical

Meeting, Banff, Canada. May.

11) Standing, M.B. and Katz, D.L., 1942. Density of Natural Gases. Trans. AIME,

146: 140−149.

12) Gas Processors Suppliers Association, 1972 (Revised 1974). Engineering Data

Book. GPSA, Tulsa: 16−2.

SOME BASIC CONCEPTS IN RESERVOIR ENGINEERING 42

13) Katz, D.L., et. al., 1959. Handbook of Natural Gas Engineering. McGraw-Hill, Inc.,

New York.

14) Takacs, G., 1976. Comparisons made for Computer Z−Factor Calculations. The

Oil and Gas Journal, Dec. 20th: 64−66.

15) Hall, K.R. and Yarborough, L., 1974. How to Solve Equation of State for

Z−Factors. The Oil and Gas Journal, Feb. 18th: 86−88.

16) Bruns, J.R., Fetkovitch, M.J. and Meitzen, V.C., 1965. The Effect of Water Influx

on p/Z−Cumulative Gas Production Curves. J.Pet.Tech., March: 287−291.

17) Agarwal, R.G., Al-Hussainy, R. and Ramey, H.J., Jr., 1965. The Importance of

Water Influx in Gas Reservoirs. J.Pet.Tech., November: 1336−1342. Trans.

AIME.

18) McCain, W.D. Jr., 1973. The Properties of Petroleum Fluids. Petroleum

Publishing Co., Tulsa.

19) Brown, G.G., Katz, D.L., Oberfell, G.B. and Alden, R.C., 1948. Natural Gasoline

and Volatile Hydrocarbons. NGAA, Tulsa.

CHAPTER 2

PVT ANALYSIS FOR OIL

2.1 INTRODUCTION

In Chapter 1, the importance of PVT analysis was stressed for relating observed

volumes of gas production at the surface to the corresponding underground withdrawal.

For gas this relationship could be obtained merely by determining the single or two

phase Z−factor, and using it in the equation of state. The basic PVT analysis required

to relate surface production to underground withdrawal for an oil reservoir is

necessarily more complex due to the presence, below the bubble point pressure, of

both a liquid oil and free gas phase in the reservoir.

This chapter concentrates on defining the three main parameters required to relate

surface to reservoir volumes, for an oil reservoir, and then proceeds to describe how

these parameters can be determined in the laboratory by controlled experiments

performed on samples of the crude oil.

The subject is approached from a mechanistic point of view in merely recognising that

PVT parameters can be determined as functions of pressure by routine laboratory

analysis. No attempt is made to describe the complex thermodynamic processes

implicit in the determination of these parameters. For a more exhaustive treatment of

the entire subject the reader is referred to the text of Amyx, Bass and Whiting

Finally, a great deal of attention is paid to the conversion of PVT data, as presented by

the laboratory, to the form required in the field. The former being an absolute set of

measurements while the latter depend upon the manner of surface separation of the

gas and oil.

2.2 DEFINITION OF THE BASIC PVT PARAMETERS

The Pressure−Volume−Temperature relation for a real gas can be uniquely defined by

the simple equation of state

pV = ZnRT (1.15)

in which the Z−factor, which accounts for the departure from ideal gas behaviour, can

be determined as described in Chapter 1, sec. 5. Using this equation, it is a relatively

simple matter to determine the relationship between surface volumes of gas and

volumes in the reservoir as

p1 p

E35.37(scf/rcf)

pTZ ZT

=××=

(1.25)

Unfortunately, no such simple equation of state exists which will describe the PVT

properties of oil. Instead, several, so-called, PVT parameters must be measured by

laboratory analysis of crude oil samples. The parameters can then be used to express

PVT ANALYSIS FOR OIL 44

the relationship between surface and reservoir hydrocarbon volumes, equivalent to

equ. (1.25).

The complexity in relating surface volumes of hydrocarbon production to their

equivalent volumes in the reservoir can be appreciated by considering fig. 2.1.

oil

stock tank

oil

(a)

solution gas

gas

oil

stock tank

oil

(b)

free gas

solution gas

SURFACE

RESERVOIR

Fig. 2.1 Production of reservoir hydrocarbons (a) above bubble point pressure,

(b) below bubble point pressure

Above the bubble point only one phase exists in the reservoir − the liquid oil. If a

quantity of this undersaturated oil is produced to the surface, gas will separate from the

oil as shown in fig. 2.1(a), the volume of the gas being dependent on the conditions at

which the surface separation is effected. In this case, it is relatively easy to relate the

surface volumes of oil and gas to volumes at reservoir conditions since it is known that

all the produced gas must have been dissolved in the oil in the reservoir.

If the reservoir is below bubble point pressure, as depicted in fig. 2.1(b), the situation is

more complicated. Now there are two hydrocarbon phases in the reservoir, gas

saturated oil and liberated solution gas. During production to the surface, solution gas

will be evolved from the oil phase and the total surface gas production will have two

components; the gas which was free in the reservoir and the gas liberated from the oil

during production. These separate components are indistinguishable at the surface and

the problem is, therefore, how to divide the observed surface gas production into

liberated and dissolved gas volumes in the reservoir.

Below bubble point pressure there is an additional complication in that the liberated

solution gas in the reservoir travels at a different velocity than the liquid oil, when both

are subjected to the same pressure differential. As will be shown in Chapter 4, sec. 2,

the flow velocity of a fluid in a porous medium is inversely proportional to the fluid

viscosity. Typically, gas viscosity in the reservoir is about fifty times smaller than for

liquid oil and consequently, the gas flow velocity is much greater. As a result, it is

normal, when producing from a reservoir in which there is a free gas saturation, that

gas will be produced in disproportionate amounts in comparison to the oil. That is, one

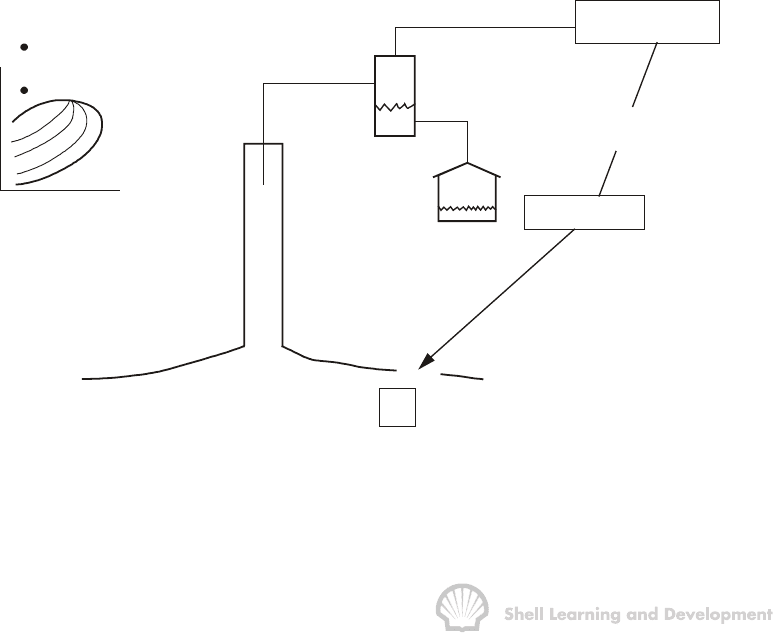
PVT ANALYSIS FOR OIL 45

barrel of oil can be produced together with a volume of gas that greatly exceeds the

volume originally dissolved per barrel of oil above bubble point pressure.

Control in relating surface volumes of production to underground withdrawal is gained

by defining the following three PVT parameters which can all be measured by

laboratory experiments performed on samples of the reservoir oil, plus its originally

dissolved gas.

− The solution (or dissolved) gas oil ratio, which is the number of standard

cubic feet of gas which will dissolve in one stock tank barrel of oil when

both are taken down to the reservoir at the prevailing reservoir pressure

and temperature (units − scf. gas/stb oil).

− The oil formation volume factor, is the volume in barrels occupied in the

reservoir, at the prevailing pressure and temperature, by one stock tank

barrel of oil plus its dissolved gas (units – rb (oil + dissolved gas)/stb oil).

− The gas formation volume factor, which is the volume in barrels that one

standard cubic foot of gas will occupy as free gas in the reservoir at the

prevailing reservoir pressure and temperature (units − rb free gas/ssf gas).

Both the standard cubic foot (scf) and the stock tank barrel (stb) referred to in the

above definitions are defined at standard conditions, which in this text are taken as

60°F and one atmosphere (14.7 psia). It should also be noted that R

and B

are both

measured relative to one stock tank barrel of oil, which is the basic unit of volume used

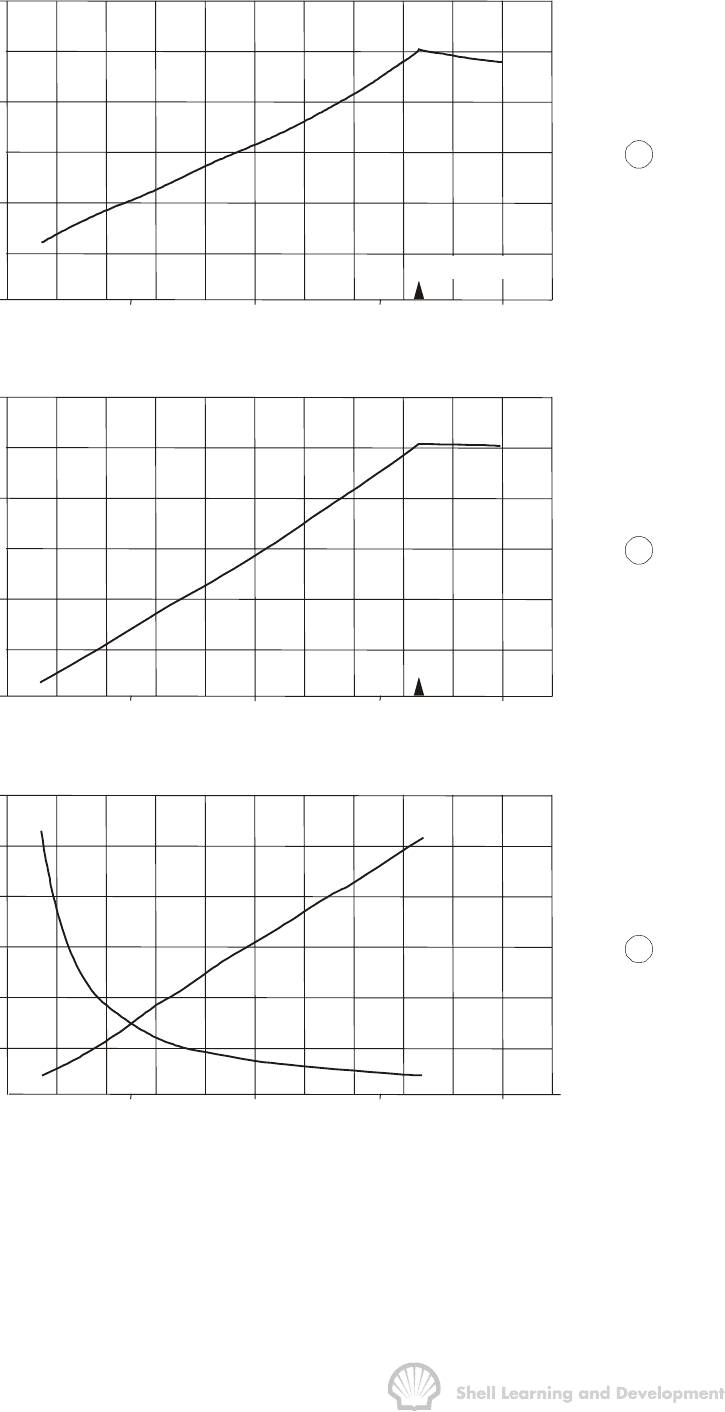
in the field. All three parameters are strictly functions of pressure, as shown in fig. 2.5,

assuming that the reservoir temperature remains constant during depletion.

Precisely how these parameters can be used in relating measured surface volumes to

reservoir volumes is illustrated in figs. 2.2 and 2.3.

Phase diagram

rb ( oil + dissolved gas) / stb

1 stb oil

R scf / stb

solution gas

Fig. 2.2 Application of PVT parameters to relate surface to reservoir hydrocarbon

volumes; above bubble point pressure.

PVT ANALYSIS FOR OIL 46

Fig. 2.2 depicts the situation when the reservoir pressure has fallen from its initial value

to some lower value p, which is still above the bubble point. As shown in the P−T

diagram (inset) the only fluid in the reservoir is undersaturated liquid oil. When this oil is

produced to the surface each stock tank barrel will yield, upon gas oil separation, R

standard cubic feet of gas. Since the oil is undersaturated with gas, which implies that it

could dissolve more if the latter were available, then the initial value of the solution gas

oil ratio must remain constant at R

(scf/stb) until the pressure drops to the bubble

point, when the oil becomes saturated, as shown in fig. 2.5(b).

Figure 2.2 also shows, in accordance with the definitions of B

and R

, that if R

scf of

gas are taken down to the reservoir with one stb of oil, then the gas will totally dissolve

in the oil at the reservoir pressure and temperature to give a volume of B

rb of oil plus

dissolved gas. Figure 2.5(a) shows that B

increases slightly as the pressure is reduced

from initial to the bubble point pressure. This effect is simply due to liquid expansion

and, since the compressibility of the undersaturated oil in the reservoir is low, the

expansion is relatively small.

Typical values of B

and R

above the bubble point are indicated in fig. 2.5, these are

the plotted results of the laboratory analysis presented in table 2.4. The initial value of

the oil formation volume factor B

is 1.2417 which increases to 1.2511 at the bubble

point. Thus initially, 1.2417 reservoir barrels of oil plus its dissolved gas will produce

one stb of oil. This is a rather favourable ratio indicating an oil of moderate volatility

and, as would be expected in this case, the initial solution gas oil ratio is also relatively

low at 510 scf/stb. Under less favourable circumstances, for more volatile oils, B

can

have much higher values. For instance, in the Statfjord field in the North Sea, B

2.7 rb/stb while the value of R

is approximately 3000 scf/stb. Obviously the most

favourable value of B

is as close to unity as possible indicating that the oil contains

hardly any dissolved gas and reservoir volumes are approximately equal to surface

volumes. The small oil fields of Beykan and Kayaköy in the east of Turkey provide good

examples of this latter condition having values of B

and R

of 1.05 and 20 scf/stb

respectively.

Below the bubble point the situation is more complicated as shown in fig. 2.3.

PVT ANALYSIS FOR OIL 47

rb ( oil + dissolved gas) / stb

1 stb oil

(R - R ) B

rb (free gas) / stb

R = R +

(R - R ) scf / stb

Fig. 2.3 Application of PVT parameters to relate surface to reservoir hydrocarbon

volumes; below bubble point pressure

In this case each stock tank barrel of oil is produced in conjunction with R scf of gas,

where R (scf/stb) is called the instantaneous or producing gas oil ratio and is measured

daily. As already noted, some of this gas is dissolved in the oil in the reservoir and is

released during production through the separator, while the remainder consists of gas

which is already free in the reservoir. Furthermore, the value of R can greatly exceed

, the original solution gas oil ratio, since, due to the high velocity of gas flow in

comparison to oil, it is quite normal to produce a disproportionate amount of gas. This

results from an effective stealing of liberated gas from all over the reservoir and its

production through the relatively isolated offtake points, the wells. A typical plot of R as

a function of reservoir pressure is shown as fig. 2.4.

scf / stb

R = R

510 scf / stb

Reservoir

ressure

4000 scf / sfb

Fig. 2.4 Producing gas oil ratio as a function of the average reservoir pressure

for a typical solution gas drive reservoir

PVT ANALYSIS FOR OIL 48

The producing gas oil ratio can be split into two components as shown in fig. 2.3, i.e.

R = R

+(R−R

)

The first of these, R

scf/stb, when taken down to the reservoir with the one stb of oil,

will dissolve in the oil at the prevailing reservoir pressure to give B

rb of oil plus

dissolved gas. The remainder, (R − R

) scf/stb, when taken down to the reservoir will

occupy a volume

sg sg

scf rb

(R R ) B (R R ) B (rb. free gas / stb)

stb scf

æö æö

−×=− −

ç÷ ç÷

èø èø

(2.1)

and therefore, the total underground withdrawal of hydrocarbons associated with the

production of one stb of oil is

(Underground withdrawal)/stb = B

+ (R − R

) B

(rb/stb) (2.2)

The above relationship shows why the gas formation volume factor has the rather

unfortunate units of rb/scf. It is simply to convert gas oil ratios, measured in scf/stb,

directly to rb/stb to be compatible with the units of B

. While B

is used almost

exclusively in oil reservoir engineering its equivalent in gas reservoir engineering is E,

the gas expansion factor, which was introduced in the previous chapter and has the

units scf/rcf. The relation between B

and E is therefore,

rb 1

scf 5.615E

æö

ç÷

èø

(2.3)

thus B

has always very small values; for a typical value of E of, say, 150 scf/rcf the

value of B

would be .00119 rb/scf.

PVT ANALYSIS FOR OIL 49

(rb / stb)

1.3

1.2

1.1

1.0

1000 2000 3000 4000

PRESSURE (psia)

p = 3330 psia

600

400

200

(scf / stb)

1000 2000 3000 4000

(rb / scf)

.010

.008

.006

.004

.002

(scf / rcf)

- 200

- 100

- 0

PRESSURE (psia)

Fig. 2.5 PVT parameters (B

, R

and B

), as functions of pressure, for the analysis

presented in table 2.4; (p

= 3330 psia).