Comon H. etc. Tree Automata Techniques and Applications

Подождите немного. Документ загружается.

3.6 Bibliographic Notes 111

which do not share variables in [DT90], for shallow systems in [Com95], for right

linear monadic rewrite systems [Sal88], for linear semi-monadic rewrite systems

[CG90], also called (with slight diﬀerences) growing systems in [Jac96]. Grow-

ing systems are the currently most general class for which the preservation of

recognizability is known.

As already pointed out, the decidability of the encompassment theory implies

the decidability of ground reducibility. There are several papers written along

these lines which will be explained in the next chapter.

Finally, approximations of the reachable terms are computed in [Gen97]

using tree automata techniques, which implies the decision of some safety prop-

erties.

3.6.7 Other applications

The relationship between ﬁnite tree automata and higher-order matching is

studied in [CJ97b].

Finite tree automata are also used in logic programming [FSVY91], type

reconstruction [Tiu92] and automated deduction [GMW97].

For further applications of tree automata in the direction of program veriﬁ-

cation, see e.g. chapter 5 of this book or e.g. [Jon87].

TATA — November 18, 2008 —

Chapter 4

Automata with Constraints

4.1 Introduction

A typical example of a language which is not recognized by a ﬁnite tree au-

tomaton is the set of terms {f (t, t) | t ∈ T (F)}, i.e. the set of ground instances

of the term f(x, x). The reason is that the two sons of the ro ot are recognized

independently and only a ﬁxed ﬁnite amount of information can be carried up

to the root position, whereas t may be arbitrarily large. Therefore, as seen

in the application section of the previous chapter, this imposes some linearity

conditions, typically when automata techniques are applied to rewrite systems

or to sort constraints. The shift from linear to non linear situations can also be

seen as a generalization from tree automata to DAG (directed acyclic graphs)

automata. This is the purpose of the present chapter: how is it possible to

extend the deﬁnitions of tree automata in order to carry over the applications

of the previous chapter to (some) non-linear situations?

Such an extension has been studied in the early 80’s by M. Dauchet and J.

Mongy. They deﬁne a class of automata which (when working in a top-down

fashion) allow duplications. Considering bottom-up automata, this amounts to

check equalities between subtrees. This yields the RATEG class. This class

is not closed under complement. If we consider its closure, we get the class

of automata with equality and disequality constraints. This class is studied in

Section 4.2.

Unfortunately, the emptiness problem is undecidable for the class RATEG

(and hence for automata with equality and disequality constraints).

Several decidable subclasses have been studied in the literature. The most

remarkable ones are:

• The class of automata with constraints between brothers which, roughly,

allows equality (or disequality) tests only between positions with the same

ancestors. For instance, the above set of terms f(t, t) is recognized by such

an automaton. This class is interesting because most important properties

of tree automata (Boolean closure and decision results) carry over this

extension and hence most of the applications of tree automata can be

extended, replacing linearity conditions with corresponding restrictions

on non-linearities.

We study this class in Section 4.3.

TATA — November 18, 2008 —

114 Automata with Constraints

• The class of reduction automata which, roughly, allows arbitrary disequal-

ity constraints but only a ﬁxed ﬁnite amount of equality constraints on

each run of the automaton. For instance the above set of terms f(t, t) also

belongs to this class, since recognizing the terms of this set requires only

one equality test, performed at the top position. Though closure prop-

erties have to be handled with care (with the deﬁnition sketched above,

the closure by complement is unknown for this class), reduction automata

are interesting because for example the set of irreducible terms (w.r.t. an

arbitrary, p ossibly non-linear rewrite system) is recognized by a reduction

automaton. Then the decidability of ground reducibility is a direct con-

sequence of emptiness decidability for deterministic reduction automata.

There is also a logical counterpart: the reducibility theory which is pre-

sented in the linear case in the previous chapter and which can be shown

decidable in the general case using a similar technique.

Reduction automata are studied in Section 4.4.

4.2 Automata with Equality and Disequality Con-

straints

4.2.1 The Most General Class

An equality constraint (resp. a disequality constraint) is a predicate on

T (F) written π = π

′

(resp. π 6= π

′

) where π, π

′

∈ {1, . . . , k}

∗

. Such a predicate

is satisﬁed on a term t, which we write t |= π = π

′

, if π, π

′

∈ Pos(t) and t|

= t|

′

(resp. π 6= π

′

is satisﬁed on t if π = π

′

is not satisﬁed on t).

The satisfaction relation |= is extended as usual to any Boolean combination

of equality and disequality constraints. The empty conjunction and disjunction

are respectively written ⊤ (true) and ⊥ (false).

Example 4.2.1. With the above deﬁnition, we have: f (a, f(a, b)) |= 1 = 21,

and f(a, b) |= 1 6= 2.

An automaton with equality and disequality constraints [is a tuple

(Q, F, Q

, ∆) where F is a ﬁnite ranked alphabet, Q is a ﬁnite set of states, Q

is a subset of Q of ﬁnal states and ∆ is a set of transition rules of of the form:

f(q

, . . . , q

)

−→ q

where f ∈ F, q

, . . . , q

, q ∈ Q, and c is a Boolean combination of equality

(and disequality) constraints. The state q is called target state in the above

transition rule. We write for short AWEDC the class of automata with equality

and disequality constraints.

Let A = (Q, F, Q

, ∆) ∈ AWEDC. The move relation →

is deﬁned us-

ing the satisfaction of equality and disequality constraints: let t, t

′

∈ T (F ∪

Q), then t →

′

if and only there is a context C ∈ C(F ∪ Q), some terms

, . . . , u

∈ T (F), and a transition rule f(q

, . . . , q

)

−→ q ∈ ∆, such that

t = C[f(q

), . . . , q

)], t

′

= C[q(f (u

, . . . , u

))] and f(u

, . . . , u

) |= c.

TATA — November 18, 2008 —

4.2 Automata with Equality and Disequality Constraints 115

We denote

∗

→

the reﬂexive and transitive closure of →

. As in Chapter 1, we

usually write t

∗

→

q instead of t

∗

→

q(t).

An automaton A ∈ AWEDC accepts (or recognizes) a ground term t ∈

T (F) if t

∗

→

q for some state q ∈ Q

. More generally, we also say that A accepts

t in state q iﬀ t

∗

→

q (acceptance by A is the particular case of acceptance by

A in a ﬁnal state).

The language accepted, or recognized, by an automaton A ∈ AWEDC

is the set L(A) of terms t ∈ T (F) that are accepted by A. The set of terms

t ∈ T (F) that are accepted by A in state q is denoted L(A, q).

A run is a mapping ρ from Pos(t) into ∆ such that if t(p) = f and the

target state of ρ(p) is q, then there is a transition rule f(q

, . . . , q

)

−→ q in ∆

such that for all 1 ≤ i ≤ n, the target state of ρ(pi) is q

and t|

|= c.

Note that we do not have here exactly the same deﬁnition of a run as in

Chapter 1: instead of the state, we keep also the rule which yielded this state.

This will be useful in the design of an emptiness decision algorithm for tree

automata with equality and disequality constraints.

Example 4.2.2. Balanced complete binary trees over the alphabet f (binary)

and a (constant) are recognized by the AWEDC ({q}, {f, a}, {q}, ∆) where ∆

consists of the following rules:

: a → q

: f (q, q)

1=2

−−→ q

For example, t = f(f(a, a), f(a, a)) is accepted. The mapping which associates

to every position p of t such that t(p) = a and which associates r

to every

position p of t such that t(p) = f is indeed a success ful run: for every position

p of t such that t(p) = f, t|

p·1

= t

p·2

, hence t|

|= 1 = 2.

Example 4.2.3. Consider the following AWEDC: (Q, F, Q

, ∆) with F =

{0, s, f} where 0 is a constant, s is unary and f has arity 4, Q = {q

, q

= {q

}, and ∆ consists of the following rules:

0 → q

s(q

) → q

s(q

) → q

f(q

, q

)

3=4

−−→ q

f(q

, q

) → q

f(q

, q

)

2=4

−−→ q

f(q

, q

)

14=4∧21=12∧131=3

−−−−−−−−−−−−−→ q

This automaton computes the sum of two natural numbers written in base

one in the following sense: if t is accepted by A then

t = f(t

, s

(0), s

n+m

(0))

for some t

and n, m ≥ 0. Conversely, for each n, m ≥ 0, there is a term

f(t

, s

(0), s

n+m

(0)) which is accepted by the automaton.

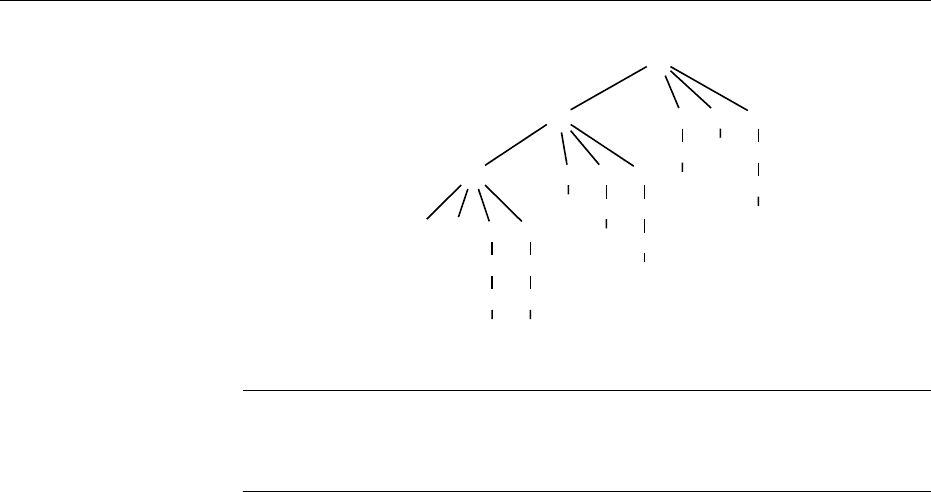
For instance the term depicted on Figure 4.1 is accepted by the automaton.

Similarly, it is possible to design an automaton of the class AWEDC which

(0) denotes s(. . . s

{z }

(0)

TATA — November 18, 2008 —

116 Automata with Constraints

0 0 s

Figure 4.1: A computation of the sum of two natural numbers

“computes the multiplication” (see exercises)

Complexity Measures

In order to evaluate the complexity of operations on automata of the class

AWEDC, we need to precise a representation of the automata and estimate the

space which is necessary for this representation.

The size of a Boolean combination of equality and disequality constraints

is deﬁned by induction:

• kπ = π

′

def

= kπ 6= π

′

def

= |π| + |π

′

| (|π| is the length of π)

• kc ∧ c

′

def

= kc ∨ c

′

def

= kck + kc

′

k + 1

• k¬ck

def

= kck

Now, the complexity of deciding whether t |= c depends on the representation

of t. If t is represented as a directed acyclic graph (a DAG) with maximal

sharing, then this can be decided in O(kck) on a RAM. Otherwise, it requires

to compute ﬁrst this representation of t, and hence can be computed in time at

most O(ktk log ktk + kck).

From now on, we assume, for complexity analysis, that the terms are rep-

resented with maximal sharing in such a way that checking an equality or a

disequality constraint on t can be completed in a time which is independent of

ktk.

The size of an automaton A ∈ AWEDC is

kAk

def

= |Q| +

f(q

,...,q

)

−→ q∈∆

n + 2 + kck

TATA — November 18, 2008 —

4.2 Automata with Equality and Disequality Constraints 117

Determinism

An automaton A in AWEDC is deterministic if for every t ∈ T (F), there is

at most one state q such that t

∗

−→

q. It is complete if for every t ∈ T (F)

there is at least one state q such that t

∗

−→

When every constraint is a tautology, then our deﬁnition of automata re-

duces to the deﬁnition of Chapter 1. However, in such a case, the notions of

determinacy do not fully coincide, as noticed in Chapter 1, page 23.

4.2.2 Reducing Non-determinism and Closure Properties

Proposition 4.2.4. For every automaton A ∈ AWEDC, there is a complete

automaton A

′

which accepts the same language as A. The size kA

′

k is poly-

nomial in kAk and the computation of A

′

can be performed in polynomial time

(for a ﬁxed alphabet). If A is deterministic, then A

′

is deterministic.

Proof. The proof is similar as for Theorem 1.1.7: we add a trash state q

⊥

and

every appropriate transition to the trash state. However, we need to be careful

concerning the constraints of the computed transitions in order to preserve the

determinism.

The additional transitions are computed as follows: for each function symbol

f ∈ F and each tuple of states (including the trash state) q

, . . . , q

, if there is no

transition f (q

, . . . , q

)

−→ q ∈ ∆, then we simply add the rule f(q

, . . . , q

) →

⊥

to ∆. Otherwise, let f (q

, . . . , q

)

−→ s

(i = 1, . . . , m) be all rules in ∆

whose left member is f(q

, . . . , q

). We add the rule f (q

, . . . , q

)

′

−→ q

⊥

to ∆,

where c

′

def

= ¬

i=1

Example 4.2.5. In order to complete the AWEDC of Example 4.2.2, we add

the following transitions:

f(q, q)

16=2

−−→ q

⊥

f(q

⊥

, q) → q

⊥

f(q, q

⊥

) → q

⊥

f(q

⊥

, q

⊥

) → q

⊥

Note that the AWEDC obtained is deterministic.

Proposition 4.2.6. For every automaton A ∈ AWEDC, there is a determin-

istic automaton A

′

which accepts the same language as A. The size kA

′

k is

exponential in kAk and A

′

can be computed in exponential time. If A is com-

plete, t hen A

′

is complete.

Proof. The construction is the same as in Theorem 1.1.9: states of A

′

are sets

of states of A. Final states of A

′

are those sets which contain at least one ﬁnal

state of A. The construction time complexity as well as the size A

′

are also of

the same magnitude as in Theorem 1.1.9. The only diﬀerence is the computation

of the constraints in transition rules: if S

, . . . , S

, S are sets of states, in the

TATA — November 18, 2008 —

118 Automata with Constraints

deterministic automaton, the rule f(S

, . . . , S

)

−→ S is labeled by a constraint

c deﬁned by:

def



q∈S

f(q

,...,q

)

−→ q∈∆

∈S

, i≤n



∧



q /∈S

f(q

,...,q

)

−→ q∈∆

∈S

, i≤n

¬c



Let us prove that a term t is accepted by A in states q

, . . . , q

(and no other

states) if and only if t is accepted by A

′

in the state {q

, . . . , q

Direction ⇒. Assume that t

−→

(i.e. t

∗

−→

in n

steps), for i = 1, . . . , k.

We prove, by induction on n = max(n

, . . . , n

), that

−−→

′

, . . . , q

If n = 1, then t is a constant and t → S is a rule of A

′

where S =

{q | a −→

q}.

Assume now that n > 1. Let, for each i = 1, . . . , k,

t = f(t

, . . . , t

)

−−→

f(q

, . . . , q

) −→

and let f(q

, . . . , q

)

−→ q

be a rule of A such that t |= c

. By induction

hypothesis, each term t

is accepted by A

′

in the states of a set S

⊇ {q

, . . . , q

Moreover, by deﬁnition of S = {q

, . . . , q

}, if t

∗

−→

′

then q

′

∈ S. Therefore,

for every transition rule of A f(q

′

, . . . , q

′

)

′

−→ q

′

such that q

′

/∈ S and q

∈ S

for every j ≤ p, we have t 6|= c

′

. Then t satisﬁes the above deﬁned constraint c.

Direction ⇐. Assume that t

−−→

′

S. We prove by induction on n that, for

every q ∈ S, and for no other state of A, t

−→

If n = 1, then S is the set of states q such that t −→

q, hence the proper ty.

Assume now that:

t = f(t

, . . . , t

)

−−→

′

f(S

, . . . , S

) −−→

′

Let f(S

, . . . , S

)

−→ S be the last rule used in this reduction. Then t |= c

and, by deﬁnition of c, for every state q ∈ S, there is a rule f(q

, . . . , q

)

−→ q

of A such that q

∈ S

for every i ≤ n and t |= c

. By induction hypoth-

esis, for each i, t

−−→

′

implies t

−−→

(for some m

< n) and hence

−→

f(q

, . . . , q

) −→

Let q /∈ S and assume that t

∗

−→

q and that the last step in this reduction

uses the transition rule f(q

, . . . , q

)

−→ q. By induction hypothesis, every

∈ S

(for i ≤ n). Hence, by deﬁnition of the constraint c, t 6|= c, and it

contradicts t

∗

−−→

′

TATA — November 18, 2008 —

4.2 Automata with Equality and Disequality Constraints 119

Thus, by construction of the ﬁnal states set, a ground term t is accepted by

′

iﬀ t is accepted by A.

Now, we have to prove that A

′

is deterministic indeed. Assume that t

∗

−−→

′

and t

∗

−−→

′

. Assume moreover that S 6= S

′

and that t is the smallest term (in

size) recognized in two diﬀerent states. Then there exists S

, . . . , S

such that

∗

−−→

′

f(S

, . . . , S

) and such that f (S

, . . . , S

)

−→ S and f(S

, . . . , S

)

′

−→ S

′

are transition rules of A

′

, with t |= c and t |= c

′

. By symmetry, we may assume

that there is a state q ∈ S such that q /∈ S

′

. Then, by construction of A

′

there are some states q

∈ S

, for every i ≤ n, and a rule f(q

, . . . , q

)

−→ q

of A where c

occurs positively in c, and is therefore satisﬁed by t, t |= c

. By

construction of the constraint of A

′

, c

must occur negatively in the second part

of (the conjunction) c

′

. Therefore, t |= c

′

contradicts t |= c

Example 4.2.7. Consider the following automaton on the alphabet F = {a, f}

where a is a constant and f is a binary symbol: Q = {q, q

⊥

}, Q

= {q} and ∆

contains the following rules:

a → q f (q, q)

1=2

−−→ q f(q, q) → q

⊥

f(q

⊥

, q) → q

⊥

f(q, q

⊥

) → q

⊥

f(q

⊥

, q

⊥

) → q

⊥

This complete (and non-deterministic) automaton accepts the same languages as

the automaton of Example 4.2.2. Then the deterministic automaton computed

as in the previous proposition is given by:

a → {q} f({q}, {q})

1=2∧⊥

−−−−−→ {q}

f({q}, {q})

1=2

−−→ {q, q

⊥

} f({q}, {q})

16=2

−−→ {q

⊥

}

f({q}, {q

⊥

}) → {q

⊥

} f({q

⊥

}, {q}) → {q

⊥

}

f({q

⊥

}, {q

⊥

}) → {q

⊥

} f({q, q

⊥

}, {q})

1=2∧⊥

−−−−−→ {q}

f({q, q

⊥

}, {q})

1=2

−−→ {q, q

⊥

} f({q, q

⊥

}, {q

⊥

}) −→ {q

⊥

}

f({q, q

⊥

}, {q, q

⊥

})

1=2

−−→ {q, q

⊥

} f({q, q

⊥

}, {q})

16=2

−−→ {q

⊥

}

f({q}, {q, q

⊥

})

1=2

−−→ {q, q

⊥

} f({q}, {q, q

⊥

})

16=2

−−→ {q

⊥

}

f({q, q

⊥

}, {q})

16=2

−−→ {q

⊥

} f({q}, {q, q

⊥

})

1=2∧⊥

−−−−−→ {q}

f({q, q

⊥

}, {q, q

⊥

})

1=2∧⊥

−−−−−→ {q} f({q

⊥

}, {q, q

⊥

}) −→ {q

⊥

}

For instance, the constraint 1=2∧⊥ is obtained by the conjunction of the label

of f (q, q)

1=2

−−→ q and the negation of the constraint labelling f(q, q) −→ q

⊥

(which is ⊤).

Some of the constraints, such as 1=2∧⊥ are uns atisﬁable, hence the corre-

sponding rules can be removed. If we ﬁnally rename the two accepting states

{q} and {q, q

⊥

} into a single state q

(this is possible since by replacing one

of these states by the other in any left hand side of a transition rule, we get

TATA — November 18, 2008 —

120 Automata with Constraints

another transition rule), then we get a simpliﬁed version of the deterministic

automaton:

a → q

f(q

⊥

, q

) → q

⊥

f(q

, q

)

1=2

−−→ q

f(q

, q

⊥

) → q

⊥

f(q

, q

)

16=2

−−→ q

⊥

f(q

⊥

, q

⊥

) → q

⊥

Proposition 4.2.8. The class AWEDC is eﬀectively closed by all Boolean op-

erations. Union requires linear time, intersection requires quadratic time and

complement requires exponential time. The respective sizes of the AWEDC ob-

tained by these construction are of the same magnitude as the time complexity.

Proof. The proof of this prop osition can be obtained from the proof of The-

orem 1.3.1 (Chapter 1, pages 30–31) with straightforward modiﬁcations. The

only diﬀerence lies in the product automaton for the intersection: we have to

consider conjunctions of constraints. More precisely, if we have two AWEDC

= (Q

, F, Q

, ∆

) and A

= (Q

, F, Q

, ∆

), we construct an AWEDC

A = (Q

× Q

, F, Q

× Q

, ∆) such that if f(q

, . . . , q

)

−→ q ∈ ∆

and

f(q

′

, . . . , q

′

)

′

−→ q

′

∈ ∆

, then f((q

, q

′

), . . . , (q

, q

′

))

c∧c

′

−−−→ (q, q

′

) ∈ ∆. The

AWEDC A recognizes L(A

) ∩ L(A

4.2.3 Decision Problems

Membership

Proposition 4.2.9. Given t ∈ T (F) and A ∈AWEDC, deciding whether t is

accepted by A can be completed in polynomial time (linear time for a determin-

istic aut omaton).

Proof. Because of the DAG representation of t, the satisfaction of a constraint

π = π

′

on t can be completed in time O(|π| + |π

′

|). Thus, if A is determinis-

tic, the membership test can be performed in time O(ktk + kAk + MC ) where

MC = max(kck



c is a constraint of a rule of A). If A is nondeterministic, the

complexity of the algorithm will be O(ktk × kAk × MC ).

Undecidability of Emptiness

Theorem 4.2.10. The emptiness problem for AWEDC is undecidable.

Proof. We reduce the Post Correspondence Problem (PCP). If w

, . . . , w

and

′

, . . . , w

′

are the word sequences of the PCP problem over the alphabet {a, b},

we let F contain h (ternary), a, b (unary) and 0 (constant). Lets recall that the

answer for the above instance of the PCP is a sequence i

, . . . , i

(which may

contain some repetitions) such that w

. . . w

= w

′

. . . w

′

If w ∈ {a, b}

∗

, w = a

. . . a

and t ∈ T (F), we write w(t) the term a

(. . . (a

(t)) . . .) ∈

T (F).

Now, we construct A = (Q, F, Q

, ∆) ∈ AWEDC as follows:

• Q contains a state q

for each preﬁx v of one of the words w

, w

′

(including

and q

′

as well as 3 extra states: q

, q and q

. We assume that a and

b are both preﬁx of at least one of the words w

, w

′

. Q

= {q

TATA — November 18, 2008 —