Comon H. etc. Tree Automata Techniques and Applications

Подождите немного. Документ загружается.

4.2 Automata with Equality and Disequality Constraints 121

w h

v h

0 0 0

′

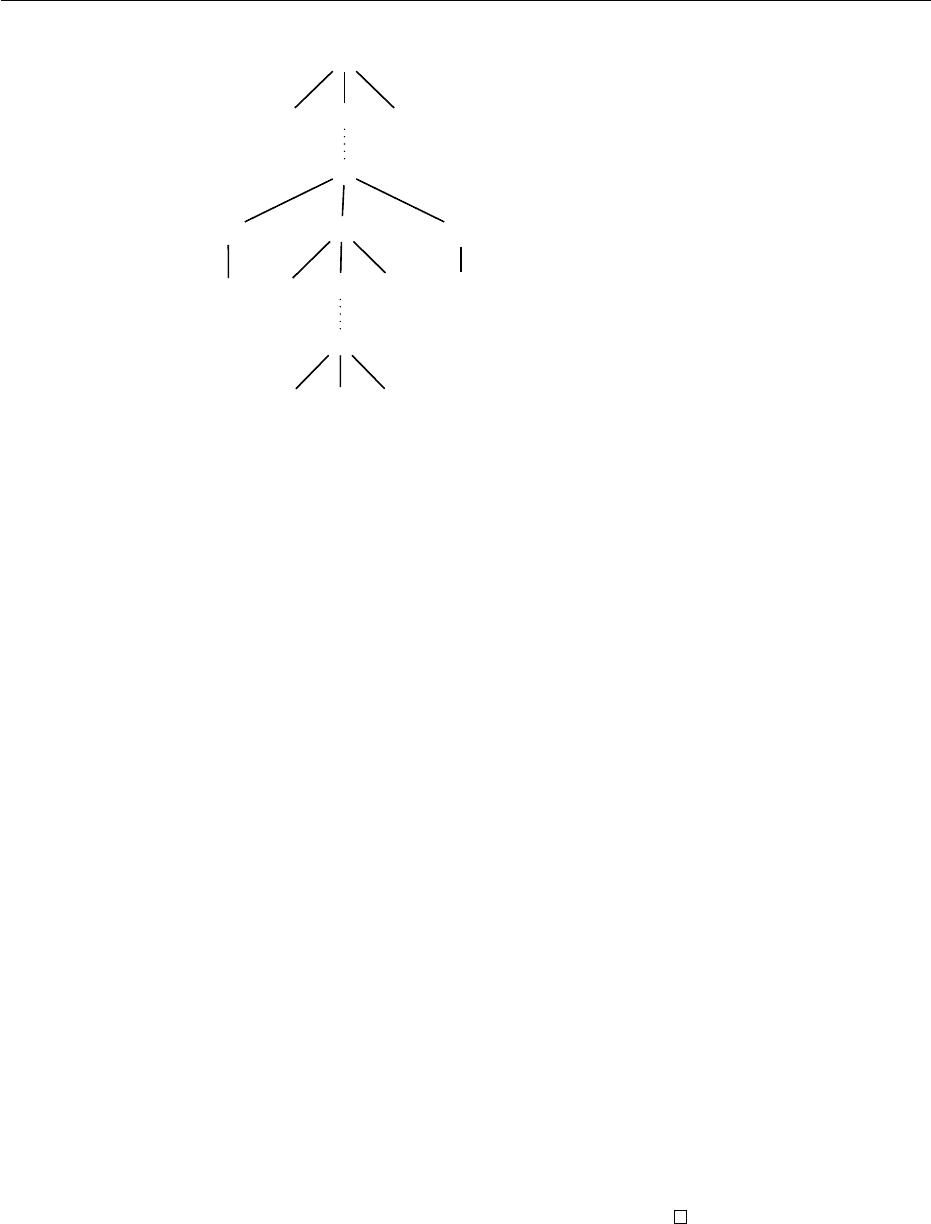
Figure 4.2: An automaton in AWEDC accepting the solutions of PCP

• ∆ contains the following rules:

a(q

) → q

b(q

) → q

a(q

) → q

a·v

if q

, q

a·v

∈ Q

b(q

) → q

b·v

if q

, q

b·v

∈ Q

a(q

) → q

b(q

) → q

a(q

′

) → q

b(q

′

) → q

∆ also contains the rules:

0 → q

h(q

, q

) → q

h(q

, q, q

′

)

1·1

=2·1∧3·1

′

=2·3

−−−−−−−−−−−−−−−→ q

h(q

, q, q

′

)

1·1

=2·1∧3·1

′

=2·3∧1=3

−−−−−−−−−−−−−−−−−−−→ q

The rule with left member h(q

, q

) recognizes the beginning of a Post

sequence. The rules with left members h(q

, q, q

′

) ensure that we are really

in presence of a successor in the PCP sequences: the constraint expresses that

the subterm at p osition 1 is obtained by concatenating some w

with the term

at position 2 · 1 and that the subterm at position 3 is obtained by concatenating

′

(with the same index i) with the subterm at position 2 · 3. Finally, entering

the ﬁnal state is subject to the additional constraint 1 = 3. This last constraint

expresses that we went through two identical words with the w

sequences and

the w

′

sequences respectively. (See Figure 4.2). The details that this automaton

indeed accepts the solutions of the PCP are left to the reader.

Then the language accepted by A is empty if and only if the PCP has a

solution. Since PCP is undecidable, emptiness of A is also undecidable.

TATA — November 18, 2008 —

122 Automata with Constraints

4.3 Automata with Constraints Between Broth-

ers

The undecidability result of the previous section led to look for subclasses which

have the desired closure properties, contain (properly) the classical tree au-

tomata and still keep the decidability of emptiness. This is the purpose of the

class AWCBB.

4.3.1 Deﬁnition

An automaton A ∈ AWEDC is an automaton with constraints between

brothers if every equality (resp. disequality) constraint has the form i = j

(resp. i 6= j) where i, j ∈ N

. AWCBB is the set of automata with constraints

between brothers.

Example 4.3.1. The set of terms {f(t, t) | t ∈ T (F)} is accepted by an au-

tomaton of the class AWCBB, because the automaton of Example 4.2.2 is in

AWCBB indeed.

4.3.2 Closure Properties

Proposition 4.3.2. AWCBB is a stable subclass of AWEDC w.r.t. Boolean

operations (union, intersection, complementation).

Proof. It is suﬃcient to check that the constructions of Propositions 4.2.4, 4.2.6

and 4.2.8 preserve the property of being a member of AWCBB.

Recall that the time complexity of each such construction is the same in

AWEDC and in the unconstrained case: union and intersection are polynomial,

complementation requires determinization and is exponential.

4.3.3 Emptiness Decision

To decide emptiness we would like to design a marking algorithm like the re-

duction algorithm of Section 1.1. Here the constraints in the transition rules

cause additional diﬃculties. For instance consider the following example.

Example 4.3.3. Let us consider the AWCBB A which contains two states q

and q

and the rules:

a → q f(q, q)

16=2

−−→ q

b → q

With the reduction algorithm of Section 1.1, we mark the state q, meaning

that this state is inhabited by at least one term (for instance a). However, this

information is not suﬃcient to ensure that one term is accepted in q

. Indeed,

in order to use the rule f (q, q)

16=2

−−→ q

, and hence pass the constraint 1 6= 2, we

need at least two distinct terms in q (for instance a and b). Note that knowing

TATA — November 18, 2008 —

4.3 Automata with Constraints Between Brothers 123

that two terms are accepted in q, we can deduce that at least two terms will be

accepted in q

(for instance f(a, b) and f(b, a)).

The basic idea for the marking algorithm below is that one can bound

the number of ”marks” (terms) needed for each state. More precisely, if we

have enough distinct terms accepted in states q

, . . . , q

, and the the transition

f(q

, . . . , q

)

−→ q is possible using some of these terms, then we know that we

have enough terms accepted in state q. In the above example, we see that the

bound is 2. We show in the next lemma that it is actually he maximal arity of a

function symbol of the signature. Let us denote maxar (F)

def

= max{ar(f) | f ∈

F}.

Lemma 4.3.4. Let A be a deterministic AWCBB on F, let f(q

, . . . , q

)

−→ q

be a transition rule of A and assume a subset L

⊆ L(A, q

) for each i ≤ n. If

there exists i ≤ n such that |L

| ≥ maxar(F) and there exists at lea st one term

t = f(t

, . . . , t

) with t

∈ L

for each i ≤ n and t |= c, then then |L(A, q)| ≥

maxar(F).

Proof. We assume without loss of generality that c is in disjunctive normal form,

and let c

′

be a conjunction in c of constraints j = j

′

or j 6= j

′

such that t |= c

′

for one t like in the lemma. Let L

= {s

, . . . , s

, . . .} (with a = maxar(F)) and

let k be the number of occurrences of q

in q

, . . . , q

. For the sake of simplicity,

we assume below that the k occurrence of q

are q

, . . . , q

If k = 1, we have f(s

, t

, . . . , t

) |= c

′

for each j ≤ a, hence f(s

, t

, . . . , t

) ∈

L(A, q) for each j ≤ a. Indeed, since A is deterministic, terms in diﬀerent states

are distinct. Hence, c

′

cannot contain an equality 1 = j with j > 1 (otherwise

it would contradict t |= c

′

) and every disequality 1 6= j in c

′

with j > 1 is still

satisﬁed by every f(s

, t

, . . . , t

). Moreover, it is clear that by hypothesis every

constraint of the form j = j

′

or j 6= j

′

with j

′

> j > 1 is still satisﬁed by every

f(s

, t

, . . . , t

If k > 1, as above, there are no equalities j = j

′

with 1 ≤ j ≤ k < j

′

≤ n in c

′

and every disequality j 6= j

′

(1 ≤ j ≤ k < j

′

≤ n) is still satisﬁed by any term of

the form f (s

, . . . , s

, t

k+1

, . . . t

) with i

, . . . , i

≤ a. It remains to study the

constraints of the form j = j

′

or j 6= j

′

with 1 ≤ j < j

′

≤ k. Assume that there

are d such disequality constraints. Then there are

(a−d+1)!

combinations of the

form f(s

, . . . , s

, t

k+1

, . . . t

) which satisfy c

′

. Since d ≤ k ≤ a, it follows that

L(A, q) contains at least a terms of this form.

Now, the marking algorithm for emptiness decision is the following:

input: AWCBB A = (Q, F, Q

, ∆)

begin

– Marked is a mapping which associates each state with a set of

terms accepted in that state.

Set Marked to the function which maps each state to the ∅

repeat

Set Marked(q) to Marked(q) ∪ {t}

where

f ∈ F

, t

∈ Marked(q

), . . . , t

∈ Marked(q

TATA — November 18, 2008 —

124 Automata with Constraints

f(q

, . . . , q

)

−→ q ∈ ∆,

t = f(t

, . . . , t

) and t |= c,

|Marked(q)| ≤ maxar(F) − 1,

until no term can be added to any Marked(q)

output: true if, for every state q

∈ Q

, Marked(q

) = ∅.

end

Theorem 4.3.5. Emptiness can be decided in polynomial time for deterministic

automata in AWCBB.

Proof. We use the above algorithm. Lemma 4.3.4 and the determinacy hy-

pothesis ens ures that it is suﬃcient to keep at most maxar(F) terms in each

state.

Theorem 4.3.6. The emptiness problem is EXPTIME-complete for (non-deterministic)

automata in AWCBB.

Proof. For non-deterministic automata, an exponential time algorithm is de-

rived from Proposition 4.2.6 (determinization) and Theorem 4.3.5.

For the EXPTIME-hardness, we may reduce to non-emptiness decision for

non-deterministic AWCBB the problem of intersection non-emptiness (for stan-

dard tree automata), which is known to be EXPTIME-complete, see Section 1.7.

Let A

,. . . ,A

be tree automata over F. We want to decide whether L(A

)∩

. . . ∩ L(A

) is empty or not.

We may assume without loss of generality that the states sets of A

,. . . ,A

(called respectively Q

,. . . ,Q

) are pairwise disjoint, and that every A

has a

single ﬁnal state called q

. We also assume that n = 2

for some integer k. If

this is not the case, let k be the smallest integer i such that n < 2

and let

′

= 2

. We consider a second instance of the above problem: A

′

,. . . ,A

′

where

′

= A

for each i ≤ n.

′

= ({q}, F, {q}, {f (q, . . . , q) → q



f ∈ F}) for each n < i ≤ n

′

Note that the tree automaton in the second case is universal, i.e. it accepts

every term of T (F). Hence, the answer is “yes” for A

′

,. . . ,A

′

iﬀ it is “yes”

for A

,. . . ,A

Now, we add a single new binary symbol g to F, getting F

′

, and consider

an AWCBB A whose language is empty iﬀ L(A

) ∩ . . . ∩ L(A

) = ∅. The idea

is that, while reading a term t bottom-up, A will simulate the computation of

each A

in several subterms t

, . . . , t

of t and will test later on (with equality

constraints) that these terms t

are all equal. For instance, for n = 4, A accepts

g(g(t

, t

), g(t

, t

)) iﬀ for all i = 1..4, A

accepts t

and moreover t

= t

and

g(t

, t

) = g(t

, t

) (hence t

= t

A = (

[

i=1

⊎ {q

, . . . , q

}, F

′

, {q

}, ∆)

where q

,. . . ,q

are new states, and the transition of ∆ are:

• every transition rule of A

, . . . , A

TATA — November 18, 2008 —

4.4 Reduction Automata 125

• for each i, 1 ≤ i ≤

, g(q

, q

2i+1

)

1=2

−−→ q

• for each i, 1 ≤ i ≤

, g(q

, q

2i+1

)

1=2

−−→ q

Note that A is non-deterministic, even if every A

is deterministic.

We can show by induction on k (n = 2

) that the answer to the intersection

non-emptiness problem is “yes” iﬀ the language recognized by A is not empty.

Moreover, the size of A is linear in the size of the initial problem and A is

constructed in a time which is linear in its size. This proves the EXPTIME-

hardness of emptiness decision for AWCBB.

4.3.4 Applications

The main diﬀerence between AWCBB and NFTA is the non-closure of AWCBB

under projection and cylindriﬁcation. Actually, the shift from automata on trees

to automata on tuples of trees cannot be extended to the class AWCBB. For

instance, choosing {0, 1}

for a signature, we have 00(00, 01) |= 1 6= 2, but this

constraint is no more valid after projection of this term on the ﬁrst component.

As long as we are interested in automata recognizing sets of trees, all results

on NFTA (and all applications) can be extended to the class AWCBB (with

a bigger complexity). For instance, Theorem 3.4.1 (sort constraints) can be

extended to interpretations of sorts as languages accepted by AWCBB. Propo-

sition 3.4.3 (encompassment) can be easily generalized to the case of non-linear

terms in which non-linearities only occur between brother positions, provided

that we replace NFTA with AWCBB. Theorem 3.4.5 can also be generalized to

the reducibility theory with predicates



where t is non-linear terms, provided

that non-linearities in t only occur between brother positions. However, we can

no longer invoke an embedding into WSkS. The important point is that the

reductibility theory only requires the weak notion of recognizability on tuples

(Rec

). Hence we do not need automata on tuples, but only tuples of automata.

As an example of application, we get a decision algorithm for ground reducibil-

ity of a term t w.r.t. left hand sides l

, . . . , l

, provided that all non-linearities

in t, l

, . . . , l

occur at brother positions: simply compute the automata A

ac-

cepting the terms that encompass l

and check that L(A) ⊆ L(A

)∪. . .∪L(A

Finally, the application on reduction strategies does not carry over to the

case of non-linear terms because it really needs automata on tuples.

4.4 Reduction Automata

As we have seen above, the ﬁrst-order theory of ﬁnitely many unary encom-

passment predicates



, . . . ,



(reducibility theory) is decidable when non-

linearities in the terms t

are restricted to brother positions. W hat happens

when we drop the restrictions and consider arbitrary terms t

, . . . , t

? It turns

out that the theory remains decidable, as we will see. Intuitively, we make im-

possible counter examples like the one in the proof of Theorem 4.2.10 (stating

undecidability of the emptiness problem for AWEDC) with an additional con-

dition that using the automaton which accepts the set of terms encompassing t,

TATA — November 18, 2008 —

126 Automata with Constraints

we may only check for a bounded number of equalities along each branch. That

is the idea of the next deﬁnitions of reduction automata.

4.4.1 Deﬁnition

A reduction automaton A is a member of AWEDC such that there is an

ordering on the states of A such that, for each rule f(q

, . . . , q

)

−→ q, q is an

upper bound of q

, . . . , q

and it is moreover a strict upper bound if c contains

an equality constraint.

In case of an automaton with ǫ-transitions q → q

′

we also require q

′

to be

not larger than q.

Example 4.4.1. Consider the set of terms on the alphabet F = {a, g} encom-

passing g(g(x, y), x). It is accepted by the following reduction automaton, the

ﬁnal state of which is q

and q

is minimal in the ordering on states.

a → q

⊤

g(q

⊤

, q

⊤

) → q

g(x,y)

g(q

⊤

, q

g(x,y)

) → q

g(x,y)

g(q

g(x,y)

, q

⊤

)

11=2

−−−→ q

g(q

g(x,y)

, q

⊤

)

116=2

−−−→ q

g(x,y)

g(q

g(x,y)

, q

g(x,y)

)

11=2

−−−→ q

g(q

g(x,y)

, q

g(x,y)

)

116=2

−−−→ q

g(x,y)

g(q, q

) → q

g(q

, q) → q

where q ∈ {q

⊤

, q

g(x,y)

, q

}

This construction can be generalized, along the lines of the proof of Propo-

sition 3.4.3 (page 97):

Proposition 4.4.2. The set of terms encompassing a term t is accepted by a

deterministic and complete reduction automaton. The size of th is automaton is

polynomial in ktk as well as the time complexity for its construction.

4.4.2 Closure Properties

As usual, we are now interested in closure properties:

Proposition 4.4.3. The class of reduction a utomata is closed under union and

intersection.

Proof. The constructions for union and intersection are the same as in the proof

of Proposition 4.2.8, and therefore, the respective time complexity and sizes are

the s ame. The proof that the class of reduction automata is closed under these

constructions is left as an exercise.

It is still unknown whether the class of reduction automata is closed under

complementation or not. As we shall see below, it is not possible to reduce the

non-determinism for reduction automata.

However, we have a weak version of stability:

Proposition 4.4.4. • With each reduction automaton, we can associate a

complete reduction automaton which accepts the same language. More-

over, t his construction preserves the determinism.

TATA — November 18, 2008 —

4.4 Reduction Automata 127

• The class of complete deterministic reduction automata is closed under

complement.

4.4.3 Emptiness Decision

Theorem 4.4.5. Emptiness is decidable for the class of complete and deter-

ministic reduction automata.

The proof of this result is quite complicated and gives quite high upper

bounds on the complexity (a tower of several exp onentials). Hence, we are not

going to reproduce it here. Let us only sketch how it works.

The idea is to use a pumping lemma in order to show that if there exists a

term recognized by a given reduction automaton A, there exists one recognized

term smaller in size than a certain bound (which depends on A). Hence, we need

to show that every term bigger than the bound can be reduced by pumping. The

equality and disequality constraints cause additional diﬃculties in the design of

a pumping lemma. For instance consider the following example.

Example 4.4.6. Let us consider a reduction automaton A with the rules:

a → q, b → q, f(q, q)

16=2

−−→ q

Now consider the term t = f (f(a, b), b) which is accepted by the automaton.

The terms f(a, b) and b yield the same state q. Hence, if there was no disequality

constraints in A (i.e. if A were a classical ﬁnite tree automaton), we may replace

f(a, b) with b in t and get a smaller term f (b, b) which is still accepted by A.

However, this is not the case here since f (b, b) which is not accepted because

f(b, b) 6|= 1 6= 2. The reason of this phenomenon is easy to understand: some

constraint which was satisﬁed before the pumping is no longer valid after the

pumping.

Consider some term t bigger than the bound, and accepted by A with a run

r. We want to perform a pumping in r giving a succes sful run r

′

on a term

′

strictly smaller than t. Here the problem is to preserve the satisfaction of

equality and disequality constraints along term replacements.

Preserving the equality constraints. Concerning equality constraints, we

deﬁne an equivalence relation between positions (of equal subtrees). It dep ends

on the run r considered. We have the following properties for the equivalence

classes:

ﬁrst, their cardinality can be bounded by a number which only depends on the

automaton, because of the condition with the ordering on states (this is

actually not true for the class AWCBB).

second, we can compute a bound b

(which only depends on the automaton)

such that the diﬀerence of the lengths of two equivalent positions is smaller

than b

TATA — November 18, 2008 —

128 Automata with Constraints

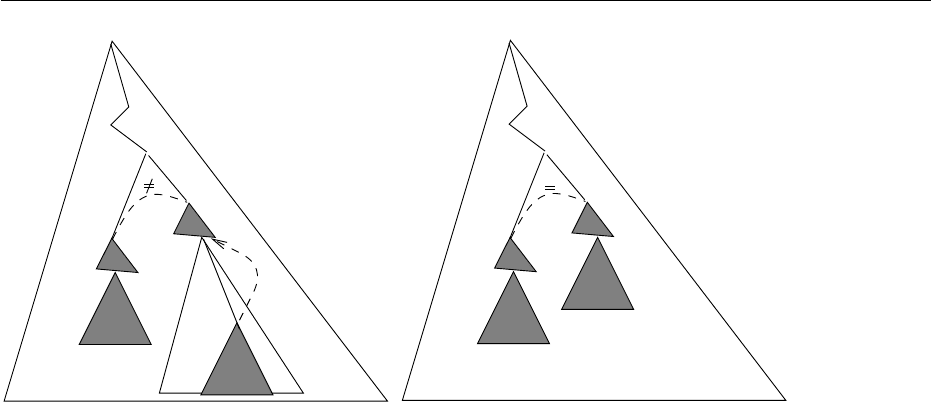
π π

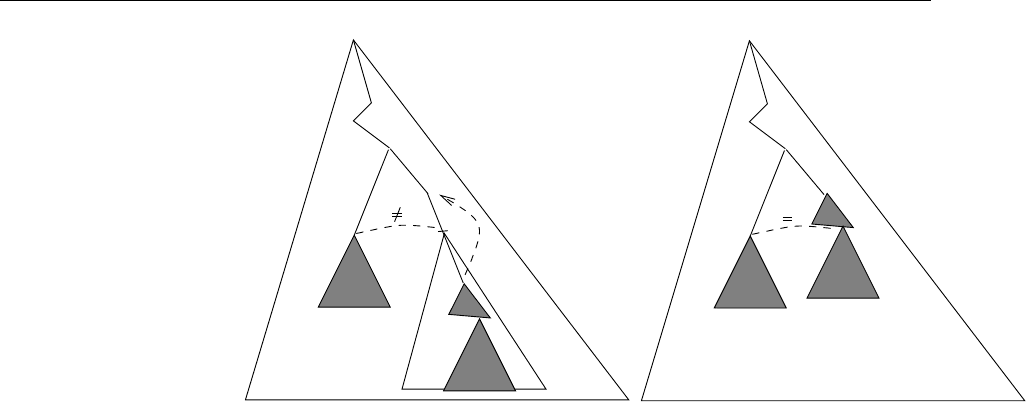
Figure 4.3: A close equality is created

Nevertheless, equalities are not a real problem, as soon as the automaton is

deterministic. Indeed, pumping can then be deﬁned on equivalence classes of

positions.

If the automaton is not deterministic, we cannot anymore guarantee that we

reach the same state at two equivalent positions. Actually, deﬁning a pumping

for non deterministic reduction automata is not possible, according to Theo-

rem 4.4.7 below.

Preserving the disequality constraints. Handling disequalities requires

more care; the number of distinct subterms in a minimal accepted term cannot

be bounded (in contrast, this number can be bounded by |Q| × N, where N is

the maximal arity of a function symbol, for AWCBB).

The problem is the possible “overlap” of disequalities checked by the au-

tomaton. As in Example 4.4.6, a pumping may yield a term which is no longer

accepted, since a disequality checked somewhere in the term is no longer sat-

isﬁed. In such a case, we say that the pumping creates an equality. Then, we

distinguish two kinds of equalities created by a pumping: the close equali-

ties and the remote equalities. Roughly, an equality created by a pump-

ing (t[v(u)]

, t[u]

) is a pair of positions (π · π

, π · π

) of t[v(u)]

which was

checked for disequality by the run ρ at position π on t[v(u)]

and such that

t[u]

π·π

= t[u]

π·π

(π is the longest common preﬁx to both members of the

pair). This equality (π · π

, π · π

) is a close equality if π ≤ p < π · π

π ≤ p < π · π

. Otherwise (p ≥ π · π

or p ≥ π · π

), it is a remote equality. The

diﬀerent situations are depicted on Figures 4.3 and 4.4.

One possible proof sketch is

• First show that it is suﬃcient to consider equalities that are created at

positions around which the states are incomparable w.r.t. >

• Next, show that, for a deep enough path, there is at least one pumping

TATA — November 18, 2008 —

4.4 Reduction Automata 129

π π

Figure 4.4: A remote equality is created

which does not yield a close equality (this makes use of a combinatorial

argument; the bound is an exponential in the maximal size of a constraint).

• For remote equalities, pumping is not suﬃcient. However, if some pump-

ing creates a remote equality anyway, this means that there are “big”equal

terms in t. Then we switch to another branch of the tree, combining pump-

ing in both subtrees to ﬁnd one (again using a combinatorial argument)

such that no equality is created.

Of course, this is a very sketchy proof. The reader is referred to the bibliog-

raphy for more information about the proof.

Theorem 4.4.7. Emptiness is not decidable for (non deterministic) reduction

automata.

Proof. We reduce the halting problem for 2-counters machines. Let us consider

a 2-counters machine with states p

(initial), p

, . . . , p

is the unique ﬁnal

state, and we assume wlog that it cannot be reentered by M). The transitions

of M have the form: p(x

, x

)

−→ p

′

, x

′

) where p, p

′

are states of M and

, x

′

, x

′

are the respective contents of the 2 counters, where x

′

is x

+ 1

or x

− 1 or x

. The condition c is a combination of x

= 0 and x

6= 0

(i = 1, 2). The problem is to decide whether p

(0, 0)

∗

−−→

(0, 0). We reduce it

to the emptiness problem for a reduction automaton which recognizes the term

representations of successful computations of M.

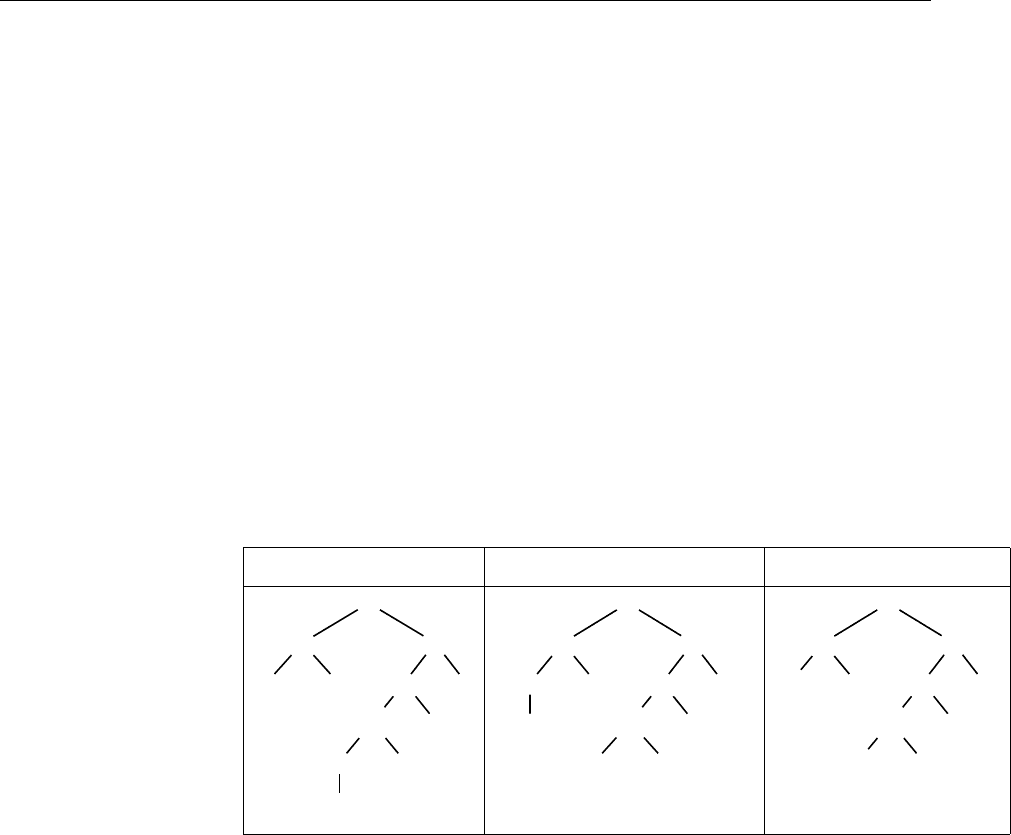
We consider a term representation of computations of M with some redun-

dancy. For this purpose, we use the following signature:

F = {0 : 0, # : 0, s : 1, p

, . . . , p

: 2, g : 2, h : 2, h

′

: 2}

A conﬁguration p(n, m) of M is represented by the term p(s

(0), s

(0)).

TATA — November 18, 2008 —

130 Automata with Constraints

A transition of M between a conﬁguration c and a conﬁguration c

′

is represented

by a term g(c, h(g(c

′

, y), y)), where y repres ents the rest of a computation of M.

Some examples of transitions are given in Figure 4.5.

The term in Figure 4.6 represents a computation sequence of conﬁgurations

, . . . , c

, with c

= p

(0, 0) and c

= p

(0, 0) and the transition of M between

and c

i+1

is denoted T

. In Figure 4.6, the nodes are decorated with the

states of A in which they are accepted. We describe below these states and the

transitions of A which permit the recognition of such a term.

The states of A are q

(for #), q

(for 0) and q

(for strictly positive integers),

a universal state q

∀

(in which any term is accepted), and, for every transition

T : ℓ → r of M, some states q

ℓ

, q

, and q

. Finally, A contains also a

state q for chaining the transitions of M and a ﬁnal state q

The transitions for recognizing integers are simply:

0 → q

, s(q

) → q

, s(q

) → q

We have also some transitions ensuring that every term is accepted in the uni-

versal state q

∀

: 0 → q

∀

, # → q

∀

, s(q

∀

) → q

∀

, p

∀

, q

∀

) → q

∀

,. . .

We associate ﬁve transitions of A to every transition T of M. Let us describe

below three examples of this construction (the other cases are similar).

p(x

, x

) → p

′

+ 1, x

) p(x

, x

)

6=0

−−−→ p

′

− 1, x

) p(x

, x

)

−−−→ p

′

, x

)

′

0 x

′

0 x

Figure 4.5: Transitions of the 2-counter machine

For the ﬁrst transition T

= ℓ

→ r

in Figure 4.5 (with ℓ

= p(x

, x

) and

= p

′

+1, x

)), we have the following transitions of the reduction automata

A (q

is an abbreviation for q

or q

p(q

, q

) → q

ℓ

′

, q

) → q

g(q

, q

∀

) → q

h(q

, q

∀

) → q

g(q

ℓ

, q

)

11=21111∧12=2112∧22=212

−−−−−−−−−−−−−−−−−−→ q

These transitions permit the recognition by A of a term of the form described

in Figure 4.5. Note that both occurrences of y in this ﬁgure are recognized in

the universal state q

∀

. It means that nothing is checked in these subterms. The

constraints in the last transition above guaranty the equality between the two

occurrences of x

, x

and y, respectively.

TATA — November 18, 2008 —