Cohen I.M., Kundu P.K. Fluid Mechanics

Подождите немного. Документ загружается.

682 Aerodynamics

Control Surfaces

The aircraft is controlled by the pilot by moving certain control surfaces described in

the following paragraphs.

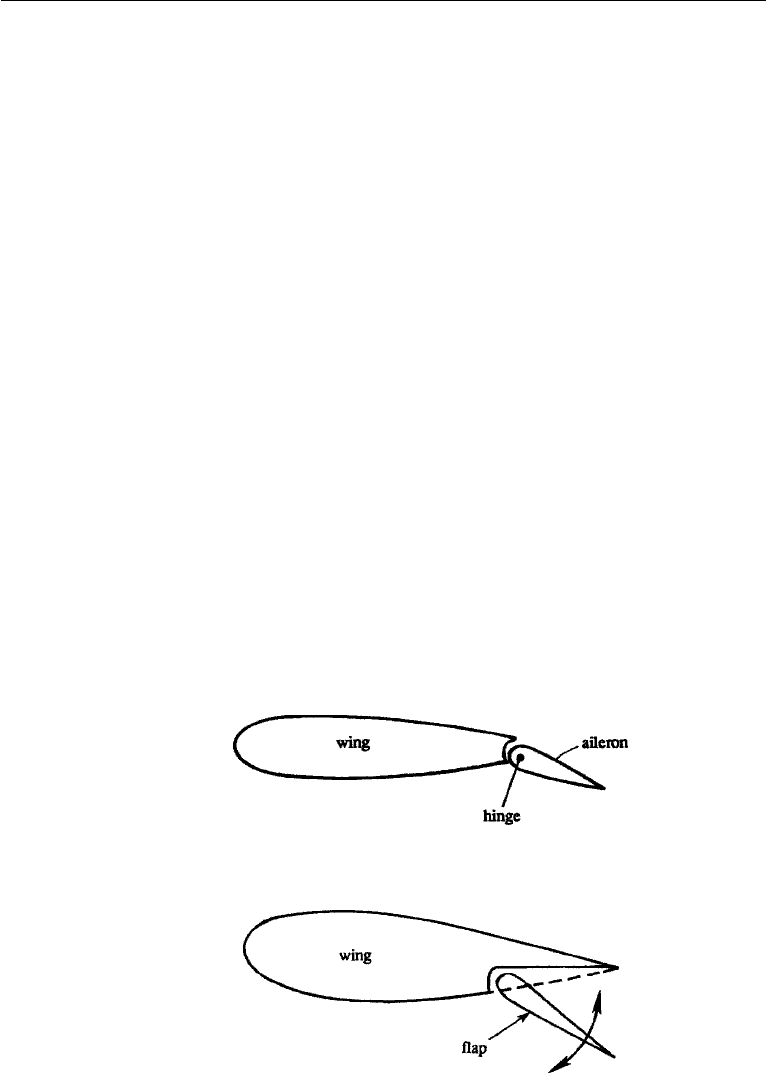
Aileron: These are portions of each wing near the wing tip (Figure 15.1), joined

to the main wing by a hinged connection, as shown in Figure 15.4. They move

differentially in the sense that one moves up while the other moves down.

A depressed aileron increases the lift, and a raised aileron decreases the lift,

so that a rolling moment results. The object of situating the ailerons near the

wing tip is to generate a large rolling moment. The pilot generally controls the

ailerons by moving a control stick, whose movement to the left or right causes

a roll to the left or right. In larger aircraft the aileron motion is controlled by

rotating a small wheel that resembles one half of an automobile steering wheel.

Elevator: The elevators are hinged to the trailing edge of the tail plane. Unlike

ailerons they move together, and their movement generates a pitching motion of

the aircraft. The elevator movements are imparted by the forward and backward

movement of a control stick, so that a backward pull lifts the nose of the aircraft.

Rudder: The yawing motion of the aircraft is governed by the hinged rear

portion of the tail ﬁn, called the rudder. The pilot controls the rudder by pressing

his feet against two rudder pedals so arranged that moving the left pedal forward

moves the aircraft’s nose to the left.

Flap: During take off, the speed of the aircraft is too small to generate enough

lift to support the weight of the aircraft. To overcome this, a section of the rear

of the wing is “split,” so that it can be rotated downward to increase the lift

(Figure 15.5). A further function of the ﬂap is to increase both lift and drag

during landing.

Figure 15.4 The aileron.

Figure 15.5 The ﬂap.

3. Airfoil Geometry 683

Modern jet transports also have “spoilers” on the top surface of each wing. When

raised slightly, they separate the boundary layer early on part of the top of the wing

and this decreases its lift. They can be deployed together or individually. Reducing

the lift on one wing will bank the aircraft so that it would turn in the direction of

the lowered wing. Deployed together, lift would be decreased and the aircraft would

descend to a new equilibrium altitude. Spoilers have another function as well. Upon

touchdown during landing they are deployed fully as ﬂat plates nearly perpendicular

to the wing surface. As such they add greatly to the drag to slow the aircraft and

shorten its roll down the runway.

An aircraft is said to be in trimmed ﬂight when there are no moments about

its center of gravity. Trim tabs are small adjustable surfaces within or adjacent to

the major control surfaces described in the preceding: ailerons, elevators, and rudder.

Deﬂections of these surfaces may be set and held to adjust for a change in the aircraft’s

center of gravity in ﬂight due to consumption of fuel or a change in the direction of

the prevailing wind with respect to the ﬂight path. These are set for steady level ﬂight

on a straight path with minimum deﬂection of the major control surfaces.

3. Airfoil Geometry

Figure 15.6 shows the shape of the cross section of a wing, called an airfoil section

(spelled aerofoil in the British literature). The leading edge of the proﬁle is generally

rounded, whereas the trailing edge is sharp. The straight line joining the centers of

curvature of the leading and trailing edges is called the chord. The meridian line of the

section passing midway between the upper and lower surfaces is called the camber

line. The maximum height of the camber line above the chord line is called the camber

of the section. Normally the camber varies from nearly zero for high-speed supersonic

wings, to ≈5% of chord length for low-speed wings. The angle α between the chord

line and the direction of ﬂight (i.e., the direction of the undisturbed stream) is called

the angle of attack or angle of incidence.

Figure 15.6 Airfoil geometry.

684 Aerodynamics

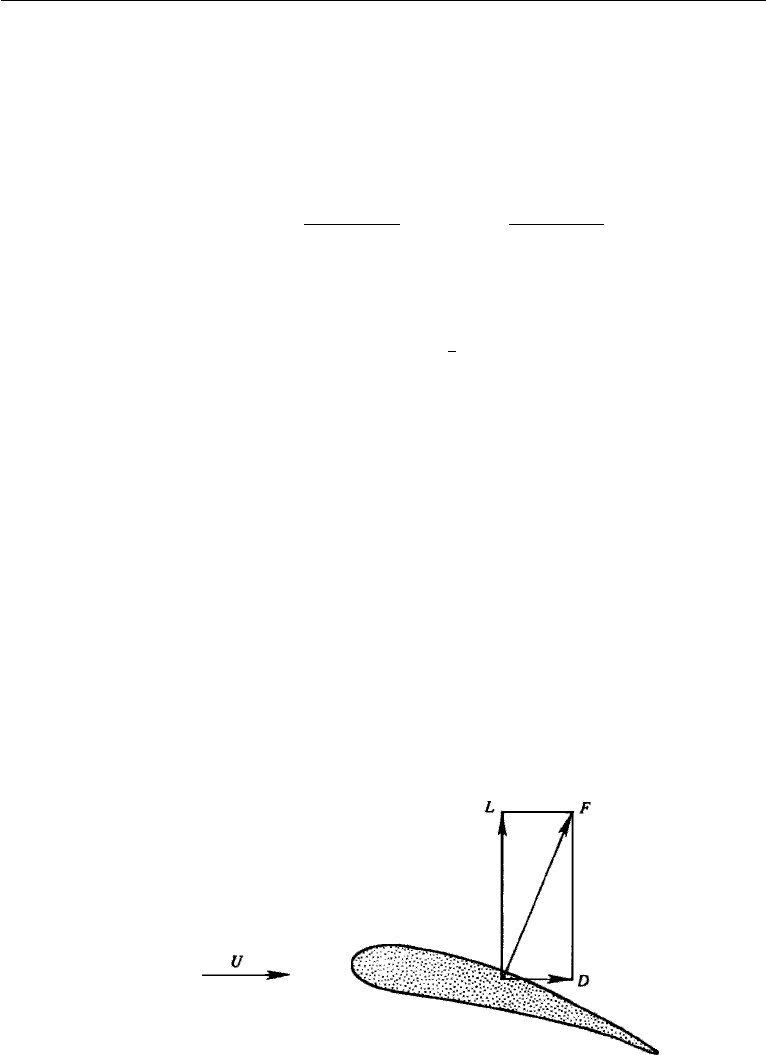
4. Forces on an Airfoil

The resultant aerodynamic force F on an airfoil can be resolved into a lift force L

perpendicular to the direction of undisturbed ﬂight and a drag force D in the direction

of ﬂight (Figure 15.7). In steady level ﬂight the drag is balanced by the thrust of

the engine, and the lift equals the weight of the aircraft. These forces are expressed

nondimensionally by deﬁning the coefﬁcients of lift and drag:

≡

(1/2)ρU

≡

(1/2)ρU

. (15.1)

The drag results from the tangential stress and normal pressure distributions on the

surface. These are called the friction drag and the pressure drag, respectively. The lift

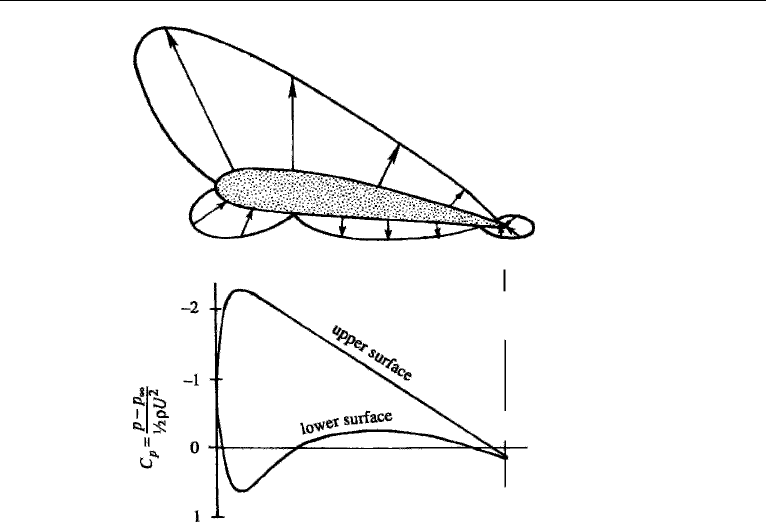
is almost entirely due to the pressure distribution. Figure 15.8 shows the distribution

of the pressure coefﬁcient C

= (p − p

∞

ρU

at a moderate angle of attack. The

outward arrows correspond to a negative C

, while a positive C

is represented by

inward arrows. It is seen that the pressure coefﬁcient is negative over most of the

surface, except over small regions near the nose and the tail. However, the pressures

over most of the upper surface are smaller than those over the bottom surface, which

results in a lift force. The top and bottom surfaces of an airfoil are popularly referred

to as the suction side and the compression side, respectively.

5. Kutta Condition

In Chapter 6, Section 11 we showed that the lift per unit span in an irrotational ﬂow

over a two-dimensional body of arbitrary cross section is

L = ρU, (15.2)

where U is the free-stream velocity and  is the circulation around the body. Relation

(15.2) is called the Kutta–Zhukhovsky lift theorem. The question is, how does a ﬂow

develop such a circulation? Obviously, a circular or elliptic cylinder does not develop

Figure 15.7 Forces on an airfoil.

5. Kutta Condition 685

Figure 15.8 Distribution of the pressure coefﬁcient over an airfoil. The upper panel shows C

plotted

normal to the surface and the lower panel shows C

plotted normal to the chord line.

any circulation around it, unless it is rotated. It has been experimentally observed that

only bodies having a sharp trailing edge, such as an airfoil, can generate circulation

and lift.

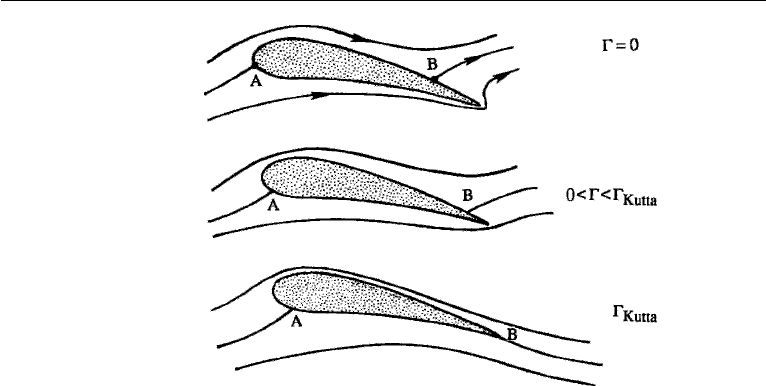
Figure 15.9 shows the irrotational ﬂow pattern around an airfoil for increasing

values of clockwise circulation. For  = 0, there is a stagnation point A located just

below the leading edge and a stagnation point B on the top surface near the trailing

edge. When some clockwise circulation is superimposed, both stagnation points move

slightly down. For a particular value of , the stagnation point B coincides with the

trailing edge. (If the circulation is further increased, the rear stagnation point moves

to the lower surface.) As far as irrotational ﬂow of an ideal ﬂuid is concerned, all

these ﬂow patterns are possible solutions. A real ﬂow, however, develops a speciﬁc

amount of circulation, depending on the airfoil shape and the angle of attack.

Consider the irrotational ﬂow around the trailing edge of an airfoil. It is shown in

Chapter 6, Section 4 that, for ﬂow in a corner of included angle γ , the velocity at the

corner point is zero if γ<180

◦

and inﬁnite if γ>180

◦

(see Figure 6.4). In the upper

two panels of Figure 15.9 the ﬂuid goes from the lower to the upper side by turning

around the trailing edge, so that γ is slightly less than 360

◦

. The resulting velocity

at the trailing edge is therefore inﬁnite in the upper two panels of Figure 15.9. In the

bottom panel, on the other hand, the trailing edge is a stagnation point because γ is

slightly less than 180

◦

686 Aerodynamics

Figure 15.9 Irrotational ﬂow pattern over an airfoil for various values of clockwise circulation.

Photographs of ﬂow around airfoils reveal that the pattern sketched in the

bottom panel of Figure 15.9 is the one developed in practice. The German aero-

dynamist Wilhelm Kutta proposed the following rule in 1902: In ﬂow over a

two-dimensional body with a sharp trailing edge, there develops a circulation of

magnitude just sufﬁcient to move the rear stagnation point to the trailing edge. This

is called the Kutta condition, sometimes also called the Zhukhovsky hypothesis.At

the beginning of the twentieth century it was merely an experimentally observed fact.

Justiﬁcation for this empirical rule became clear after the boundary layer concepts

were understood. In the following section we shall see why a real ﬂow should satisfy

the Kutta condition.

Historical Notes

According to von Karman (1954, p. 34), the connection between the lift of airplane

wings and the circulation around them was recognized and developed by three per-

sons. One of them was the Englishman Frederick Lanchester (1887–1946). He was a

multisided and imaginative person, a practical engineer as well as an amateur mathe-

matician. His trade was automobile building; in fact, he was the chief engineer and

general manager of the Lanchester Motor Company. He once took von Karman for a

ride around Cambridge in an automobile that he built himself, but von Karman “felt a

little uneasy discussing aerodynamics at such rather frightening speed.” The second

person is the German mathematician Wilhelm Kutta (1867–1944), well-known for

the Runge–Kutta scheme used in the numerical integration of ordinary differential

equations. He started out as a pure mathematician, but later became interested in

aerodynamics. The third person is the Russian physicist Nikolai Zhukhovsky, who

developed the mathematical foundations of the theory of lift for wings of inﬁnite span,

independently of Lanchester and Kutta. An excellent book on the history of ﬂight and

the science of aerodynamics was recently authored by Anderson (1998).

6. Generation of Circulation 687

6. Generation of Circulation

We shall now discuss why a real ﬂow around an airfoil should satisfy the Kutta

condition. The explanation lies in the frictional and boundary layer nature of a real

ﬂow. Consider an airfoil starting from rest in a real ﬂuid. The ﬂow immediately after

starting is irrotational everywhere, because the vorticity adjacent to the surface has

not yet diffused outward. The velocity at this stage has a near discontinuity adjacent

to the surface. The ﬂow has no circulation, and resembles the pattern in the upper

panel of Figure 15.9. The ﬂuid goes around the trailing edge with a very high velocity

and overcomes a steep deceleration and pressure rise from the trailing edge to the

stagnation point.

Within a fraction of a second (in a time of the order of that taken by the ﬂow

to move one chord length), however, boundary layers develop on the airfoil, and the

retarded ﬂuid does not have sufﬁcient kinetic energy to negotiate the steep pressure

rise from the trailing edge toward the rear stagnation point. This generates a back-ﬂow

in the boundary layer and a separation of the boundary layer at the trailing edge. The

consequence of all this is the generation of a shear layer, which rolls up into a spiral

form under the action of its own induced vorticity (Figure 15.10). The rolled-up shear

layer is carried downstream by the ﬂow and is left at the location where the airfoil

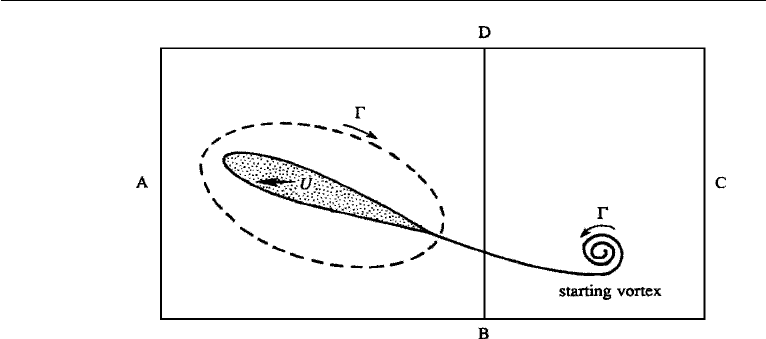
started its motion. This is called the starting vortex.

The sense of circulation of the starting vortex is counterclockwise in Figure 15.10,

which means that it must leave behind a clockwise circulation around the airfoil. To

see this, imagine that the ﬂuid is stationary and the airfoil is moving to the left.

Consider a material circuit ABCD, made up of the same ﬂuid particles and large

enough to enclose both the initial and ﬁnal locations of the airfoil (Figure 15.11).

Initially the trailing edge was within the region BCD, which now contains the starting

vortex only. According to the Kelvin circulation theorem, the circulation around any

material circuit remains constant, if the circuit remains in a region of inviscid ﬂow

(although viscous processes may go on inside the region enclosed by the circuit).

The circulation around the large curve ABCD therefore remains zero, since it was

zero initially. Consequently the counterclockwise circulation of the starting vortex

around DBC is balanced by an equal clockwise circulation around ADB. The wing is

therefore left with a circulation  equal and opposite to the circulation of the starting

vortex.

It is clear from Figure 15.9 that a value of circulation other than the one that

moves the rear stagnation point exactly to the trailing edge would result in a sequence

of events as just described and would lead to a readjustment of the ﬂow. The only value

Figure 15.10 Formation of a spiral vortex sheet soon after an airfoil begins to move.

688 Aerodynamics

Figure 15.11 A material circuit ABCD in a stationary ﬂuid and an airfoil moving to the left.

of the circulation that would not result in further readjustment is the one required by

the Kutta condition. With every change in the speed of the airﬂow or in the angle of

attack, a new starting vortex is cast off and left behind. A new value of circulation

around the airfoil is established so as to place the rear stagnation point at the trailing

edge in each case.

It is apparent that the viscosity of the ﬂuid is not only responsible for the drag,

but also for the development of circulation and lift. In developing the circulation, the

ﬂow leads to a steady state where a further boundary layer separation is prevented.

The establishment of circulation around an airfoil-shaped body in a real ﬂuid is a

remarkable result.

7. Conformal Transformation for Generating Airfoil Shape

In the study of airfoils, one is interested in ﬁnding the ﬂow pattern and pressure

distribution. The direct solution of the Laplace equation for the prescribed boundary

shape of the airfoil is quite straightforward using a computer, but analytically difﬁcult.

In general the analytical solutions are possible only when the airfoil is assumed

thin. This is called thin airfoil theory, in which the airfoil is replaced by a vortex

sheet coinciding with the camber line. An integral equation is developed for the local

vorticity distribution from the condition that the camber line be a streamline (velocity

tangent to the camber line). The velocity at each point on the camber line is the

superposition (i.e., integral) of velocities induced at that point due to the vorticity

distribution at all other points on the camber line plus that from the oncoming stream

(at inﬁnity). Since the maximum camber is small, this is usually evaluated on the

x–y-plane. The Kutta condition is represented by the requirement that the strength of

the vortex sheet at the trailing edge is zero. This is treated in detail in Kuethe and

Chow (1998, chapter 5) and Anderson (2007, chapter 4). An indirect way of solving

the problem involves the method of conformal transformation, in which a mapping

function is determined such that the arbitrary airfoil shape is transformed into a circle.

Then a study of the ﬂow around the circle would determine the ﬂow pattern around

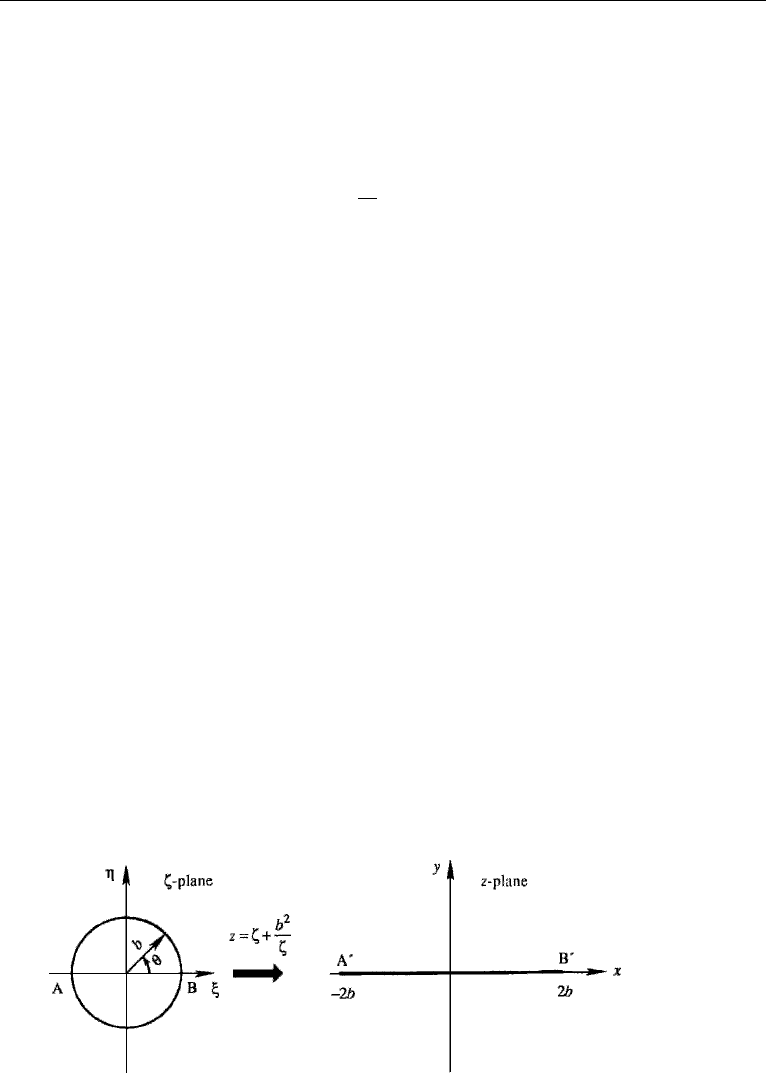
7. Conformal Transformation for Generating Airfoil Shape 689

the airfoil. This is called Theodorsen’s method, which is complicated and will not be

discussed here.

Instead, we shall deal with a case in which a given transformation maps a circle

into an airfoil-like shape and determines the properties of the airfoil generated thereby.

This is the Zhukhovsky transformation

z = ζ +

, (15.3)

where b is a constant. It maps regions of the ζ -plane into the z-plane, some examples

of which are discussed in Chapter 6, Section 14. Here, we shall assume circles of

different conﬁgurations in the ζ -plane and examine their transformed shapes in the

z-plane. It will be seen that one of them will result in an airfoil shape.

Transformation of a Circle into a Straight Line

Consider a circle, centered at the origin in the ζ -plane, whose radius b is the same as

the constant in the Zhukhovsky transformation (Figure 15.12). For a point ζ = be

iθ

on the circle, the corresponding point in the z-plane is

z = be

iθ

+ be

−iθ

= 2b cos θ.

As θ varies from 0 to π, z goes along the x-axis from 2b to −2b.Asθ varies from π

to 2π, z goes from −2b to 2b. The circle of radius b in the ζ -plane is thus transformed

into a straight line of length 4b in the z-plane. It is clear that the region outside the

circle in the ζ -plane is mapped into the entire z-plane. (It can be shown that the region

inside the circle is also transformed into the entire z-plane. This, however, is of no

concern to us, since we shall not consider the interior of the circle in the ζ -plane.)

Transformation of a Circle into a Circular Arc

Let us consider a circle of radius a (>b)intheζ -plane, the center of which is displaced

along the η-axis and which cuts the ξ -axis at (±b, 0), as shown in Figure 15.13. If a

Figure 15.12 Transformation of a circle into a straight line.

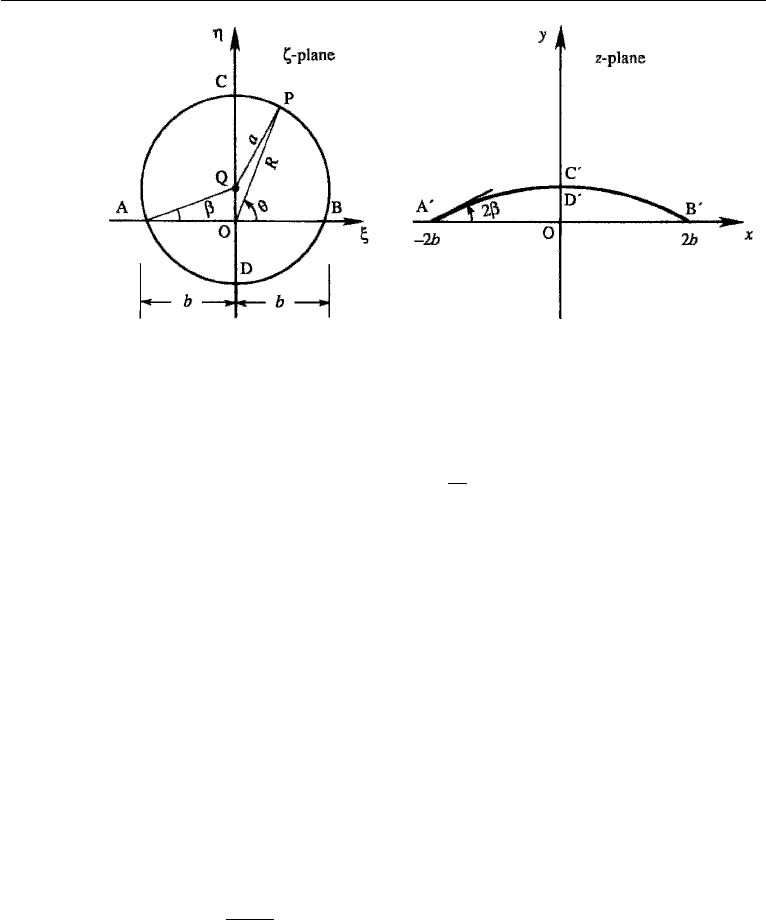
690 Aerodynamics

Figure 15.13 Transformation of a circle into a circular arc.

point on the circle in the ζ -plane is represented by ζ = Re

iθ

, then the corresponding

point in the z-plane is

z = Re

iθ

−iθ

whose real and imaginary parts are

x = (R + b

/R) cos θ,

y = (R − b

/R) sin θ.

(15.4)

Eliminating R, we obtain

sin

θ −y

cos

θ = 4b

sin

θ cos

θ. (15.5)

To understand the shape of the curve represented by equation (15.5) we must express

θ in terms of x, y, and the known constants. From triangle OQP, we obtain

= OP

+ OQ

− 2(OQ)(OP) cos (Q

OP).

Using QP = a = b/ cos β and OQ = b tan β, this becomes

cos

= R

+ b

tan

β − 2Rb tan β cos(90

◦

− θ),

which simpliﬁes to

2b tan β sin θ = R − b

/R = y/sin θ, (15.6)

where equation (15.4) has been used. We now eliminate θ between equations (15.5)

and (15.6). First note from equation (15.6) that cos

θ = (2b tan β −y)/2b tan β, and

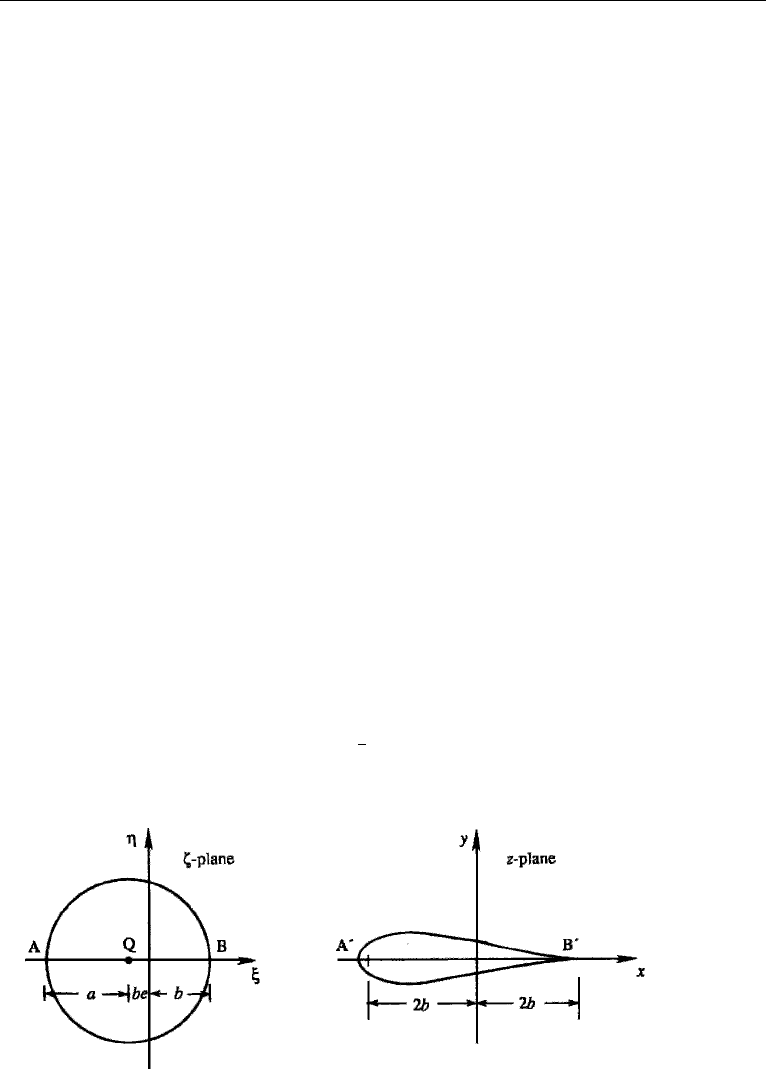
7. Conformal Transformation for Generating Airfoil Shape 691

cot

θ = (2b tan β −y)/y. Then divide equation (15.5) by sin

θ, and substitute these

expressions of cos

θ and cot

θ. This gives

+ (y + 2b cot 2β)

= (2b csc 2β)

where β is known from cos β = b/a. This is the equation of a circle in the z-plane,

having the center at (0, −2b cot 2β) and a radius of 2b csc 2β. The Zhukhovsky

transformation has thus mapped a complete circle into a circular arc.

Transformation of a Circle into a Symmetric Airfoil

Instead of displacing the center of the circle along the imaginary axis of the ζ -plane,

suppose that it is displaced to a point Q on the real axis (Figure 15.14). The radius of

the circle is a(>b), and we assume that a is slightly larger than b:

a ≡ b(1 + e) e  1. (15.7)

A numerical evaluation of the Zhukhovsky transformation (15.3), with assumed val-

ues for a and b, shows that the corresponding shape in the z-plane is a streamlined body

that is symmetrical about the x-axis. Note that the airfoil in Figure 15.14 has a rounded

nose and thickness, while the one in Figure 15.13 has a camber but no thickness.

Transformation of a Circle into a Cambered Airfoil

As can be expected from Figures 15.13 and 15.14, the transformed ﬁgure in the z-plane

will be a general airfoil with both camber and thickness if the circle in the ζ -plane is

displaced in both η and ξ directions (Figure 15.15). The following relations can be

proved for e  1:

c  4b,

camber 

βc,

max

/c  1.3 e.

(15.8)

Figure 15.14 Transformation of a circle into a symmetric airfoil.