Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models

Подождите немного. Документ загружается.

760 CHAPTER 8 Analytic Geometry and the Conic Sections 8–54

College Algebra G&M—

Solve each equation.

Graph each relation. Include vertices, x- and

y-intercepts, asymptotes, and other features.

10. 11.

12. 13.

14. a.

15. 16.

17. 18.

19.

20. 41x ⫺ 12

⫺ 361y ⫹ 22

⫽ 144

⫹ y

⫹ 10x ⫺ 4y ⫹ 20 ⫽ 0

x ⫽ y

⫹ 4y ⫹ 7f1x2⫽ log

1x ⫹ 12

q1x2⫽ 2

⫹ 3h1x2⫽

x ⫺ 2

⫺ 9

f 1x2⫽ x

⫹ x

⫺ 13x

⫺ x ⫹ 12

g1x2⫽ 1x ⫺ 321x ⫹ 121x ⫹ 42

y ⫽ 1x ⫺ 3

⫹ 1y ⫽

x ⫺ 1

⫹ 2

y ⫽

冟

x ⫺ 2

冟

⫹ 3y ⫽

x ⫹ 2

log

x ⫹ log 1x ⫺ 32⫽ 1

ln x ⫽ 2

x⫺2

⫽ 7

x⫹1

⫽

⫺ 6x ⫹ 13 ⫽ 0

⫹ 8 ⫽ 0

2x ⫺ 3

⫹ 5 ⫽ x

冟

n ⫹ 4

冟

⫹ 3 ⫽ 13

⫺ 2x

⫹ 4x ⫺ 8 ⫽ 0

21. Determine the following for

the indicated graph (write all

answers in interval notation):

(a) the domain, (b) the range,

increasing or decreasing,

(d) interval(s) where f(x) is

constant, (e) location of any

maximum or minimum value(s), (f) interval(s) where

f(x) is positive, and (g) interval(s) where f(x) is

negative.

Solve each system of equations with a graphing

calculator. Use a matrix equation for Exercise 22, and

the intersection-of-graphs method for Exercise 23.

22. 23.

24. If a person invests $5000 at 9% compounded

quarterly, how long would it take for the money to

grow to $12,000?

25. A radiator contains 10 L of liquid that is 40%

antifreeze. How much should be drained off and

replaced with pure antifreeze for a 60% mixture?

Solve each equation using a graphing calculator.

26.

27.

28.

29.

30.

x ⫹ 3

x ⫺ 4

ⱖ 3

x⫺1

⫽ 2

2⫺x

⫺ 3e

⫽ 4

0x ⫹ 40⫽ 8 ⫺ 0x0

⫺ 4x ⫹ 3 ⫽

⫺ 5

⫹ y

⫽ 25

64x

⫹ 12y

⫽ 768

•

4x ⫹ 3y ⫽ 13

⫺9y ⫹ 5z ⫽ 19

x ⫺ 4z ⫽⫺4

CUMULATIVE REVIEW CHAPTERS R–8

108642⫺10⫺8⫺6⫺4⫺2

⫺2

⫺4

⫺6

⫺8

⫺10

(⫺1, 4)

(⫺4, 0)

(2, 0)

cob19545_ch08_755-760.qxd 12/16/10 8:41 AM Page 760

College Algebra Graphs & Models—

Additional Topics

in Algebra

CHAPTER OUTLINE

9.1 Sequences and Series 762

9.2 Arithmetic Sequences 773

9.3 Geometric Sequences 782

9.4 Mathematical Induction 796

9.5 Counting Techniques 804

9.6 Introduction to Probability 816

9.7 The Binomial Theorem 829

CHAPTER CONNECTIONS

For a corporation of any size, decisions made

by upper management often depend on a large

number of factors, with the desired outcome

attainable in many different ways. For instance,

consider a legal ﬁrm that specializes in family

law, with a support staff of 15 employees—6

paralegals and 9 legal assistants. Due to recent

changes in the law, the ﬁrm wants to send some

combination of ﬁve support staff to a conference

dedicated to the new changes. In Chapter 9,

we’ll see how counting techniques and probability

can be used to determine the various ways such

a group can be randomly formed, even if certain

constraints are imposed. This application

appears as Exercise 34 in Section 9.6.

Check out these other real-world connections:

䊳

Determining the Effects of Inﬂation

(Section 9.1, Exercise 86)

䊳

Calculating Possible Movements of a Computer

Animation (Section 9.2, Exercise 77)

䊳

Counting the Number of Possible Area

Codes and Phone Numbers

(Section 9.5, Exercises 84 and 85)

䊳

Tracking and Improving Customer Service

Using Probability (Section 9.6, Exercise 53)

761

cob19545_ch09_761-773.qxd 11/9/10 8:17 PM Page 761

9.1 Sequences and Series

A sequence can be thought of as a pattern of numbers listed in a prescribed order. A

series is the sum of the numbers in a sequence. Sequences and series come in count-

less varieties, and we’ll introduce some general forms here. In following sections we’ll

focus on two special types: arithmetic and geometric sequences. These are used in a

number of different ﬁelds, with a wide variety of signiﬁcant applications.

A. Finding the Terms of a Sequence Given the General Term

Suppose a person had $10,000 to invest, and decided to place the money in government

bonds that guarantee an annual return of 7%. From our work in Chapter 5, we know the

amount of money in the account after x years can be modeled by the function

If you reinvest your earnings each year, the amount in the

account would be (rounded to the nearest dollar):

Year: f(1) f(2) f(3) f(4) f(5)

Value: $10,700 $11,449 $12,250 $13,108 $14,026

Note the relationship (year, value) is a function that pairs 1 with $10,700, 2 with

$11,449, 3 with $12,250, and so on. This is an example of a sequence. To distinguish

sequences from other algebraic functions, we commonly name the functions a instead

of f, use the variable n instead of x, and employ a subscript notation. The function

would then be written Using this notation

and so on.

The values are called the terms of the sequence. If the account

were closed after a certain number of years (for example, after the ﬁfth year) we have

a ﬁnite sequence. If we let the investment grow indeﬁnitely, the result is called an

inﬁnite sequence. The expression a

that deﬁnes the sequence is called the general or

nth term and the terms immediately preceding it are called the term, the

term, and so on.

Sequences

A ﬁnite sequence is a function a

whose domain is the set of natural numbers from

1 to n. The terms of the sequence are labeled

where a

represents an arbitrary “interior” term and also represents

the last term of the sequence.

An inﬁnite sequence is a function whose domain is the set of all

natural numbers.

EXAMPLE 1A

䊳

Computing Speciﬁed Terms of a Sequence

For ﬁnd a

, a

, and a

Solution

䊳

EXAMPLE 1B

䊳

Computing the First k Terms of a Sequence

Find the ﬁrst four terms of the sequence Write the terms of the

sequence as a list.

⫽ 1⫺12

⫽

6 ⫹ 1

⫽

7 ⫹ 1

⫽

1 ⫹ 1

⫽ 2

⫽

3 ⫹ 1

⫽

n ⫹ 1

, a

, p , a

, a

k⫹1

, p , a

n⫺1

, a

1n ⫺ 22nd

1n ⫺ 12st

, a

, p

⫽ 10,700, a

⫽ 11,449,

⫽ 10,00011.072

.f 1x2⫽ 10,00011.072

TTTTT

1x2⫽ 10,00011.072

762 9–2

College Algebra Graphs & Models—

LEARNING OBJECTIVES

In Section 9.1 you will see

how we can:

A. Write out the terms of a

sequence given the

general or nth term

B. Work with recursive

sequences and

sequences involving a

factorial

C. Find the partial sum of a

series

D. Use summation notation

to write and evaluate

series

E. Use sequences to solve

applications

WORTHY OF NOTE

Sequences can actually start with

any natural number. For instance,

the sequence must start

at to avoid division by zero. In

addition, we will sometimes use a

to indicate a preliminary or inaugural

element, as in for the

amount of money initially held, prior

to investing it.

⫽ $10,000

n ⫽ 2

⫽

n ⫺ 1

cob19545_ch09_761-773.qxd 11/9/10 8:18 PM Page 762

9–3 Section 9.1 Sequences and Series 763

College Algebra Graphs & Models—

Solution

䊳

The sequence can be written 4, 16, , or more generally as 4,

16, , to show how each term was generated.

Now try Exercises 7 through 22

䊳

Much of the beauty and power of studying sequences comes from patterns detected

within the sequence, or the ability to ﬁnd a particular term quickly. Here, the calculator

becomes an invaluable tool, aiding computations to be sure but also enabling explo-

rations not generally possible with paper and pencil alone. Most graphing calculators

offer a “seq(” feature (often in a STAT or LIST menu),

where the left parenthesis indicates we need to enter the

following four items of information: the nth term

formula deﬁning the sequence, the variable in use, the

starting value, and the ending value. The sequence gen-

erated can be seen on the home screen, or stored in a list

for future use. In Figure 9.1, this feature was used to

generate the ﬁrst four terms of the sequence deﬁned in

Example 1(B) using the keystrokes (LIST)

(OPS) 5:seq(.

In addition to the seq( feature, most calculators

have a sequence , which is especially useful

when working with several sequences simultaneously.

In sequence (Figure 9.2A), the screen

presents a very different look (Figure 9.2B), ﬁrst of all

showing that the minimum value of nis 1, then naming

the functions u(n), v(n), and w(n) instead of Y

, Y

and Y

. The entries following each, for example

“u(nMin) ⫽,” are used in a study of the recursive

sequences, which are covered later. Note that function names for the sequences (u, v,

and w) are the function for the numbers 7, 8, and 9, respectively.

2nd

MODE

STAT

2nd

p1⫺12

⫺8,⫺2,p⫺8,⫺2,

⫽ 1⫺12

⫽⫺8

⫽ 1⫺12

⫽ 16

⫽ 1⫺12

⫽⫺2

⫽ 1⫺12

⫽ 4

WORTHY OF NOTE

When the terms of a sequence

alternate in sign as in Example 1B,

we call it an alternating sequence.

Figure 9.1

Figure 9.2B

EXAMPLE 2

䊳

Finding the Terms of a Sequence Using Technology

Use a calculator in sequence to

a. Find the sixth term (as a fraction) for the sequence deﬁned in Example 1A.

b. Generate the ﬁrst ﬁve terms for the sequence deﬁned in Example 1B and store

the results in a list.

Solution

䊳

a. On the screen, deﬁne the sequence u(n)

as (Figure 9.3), leaving the

second line blank. Then go to the home screen

and access the “seq(” feature as before, and

supply the information required. Since we only

want the sixth term (a

), we enter seq(u(n), n,

6, 6) Frac, and after pressing , we obtain

the expected result (Figure 9.4).

ENTER

䉴

u1n2⫽

n ⫹ 1

MODE

Figure 9.4

Figure 9.2A

Figure 9.3

cob19545_ch09_761-773.qxd 12/17/10 12:44 AM Page 763

b. For the ﬁrst ﬁve terms, we change u(n) to

then go to the home

screen and use the “5:seq(” command once

again, this time for terms one through ﬁve.

Knowing that we want the results stored in a

list, we follow the command with

(L1) (Figure 9.5). The list is shown in

Figure 9.6.

Now try Exercises 23 through 32

䊳

B. Recursive Sequences and Factorial Notation

Sometimes the formula deﬁning a sequence uses the preceding term or terms to gener-

ate those that follow. These are called recursive sequences and are particularly useful

in writing computer programs. Because of how they are deﬁned, recursive sequences

must give an inaugural term or seed element(s), to begin the recursion process.

Perhaps the most famous recursive sequence is associated with the work of

Leonardo of Pisa (

. 1180–1250), better known to history as Fibonacci. In the

Fibonacci sequence, each successive term is the sum of the previous two, begin-

ning with 1, 1, .

EXAMPLE 3

䊳

Computing the Terms of a Recursive Sequence

Write out the ﬁrst eight terms of the Fibonacci sequence, which is deﬁned by

, and

Solution

䊳

The ﬁrst two terms are given, so we begin with

At this point we can simply use the fact that each successive term is simply the

sum of the preceding two, and ﬁnd that and

The ﬁrst eight terms are 1, 1, 2, 3, 5, 8, 13, and 21.

Now try Exercises 33 through 38

䊳

Since a recursive sequence is deﬁned using a preceding term or terms, the ﬁrst

term(s) must be given in order to determine those that follow. To generate the sequence

using technology, we enter these initial terms as “ ” on the screen,

enclosed in braces. For the Fibonacci sequence

from Example 3, we would enter ”

as shown in Figure 9.7, with the result shown in Fig-

ure 9.8 (use the right arrow to view any remaining terms).

Some sequences may involve the computation

of a factorial, which is the product of a given natu-

ral number with all those that precede it. The ex-

pression 5! is read, “ﬁve factorial,” and is evaluated

as:

Factorials

For any natural number n,

n! ⫽ n

1n ⫺ 12

1n ⫺ 22

5! ⫽ 5

1 ⫽ 120.

u1nMin2⫽ 51, 16

u1nMin2⫽

⫽ 8 ⫹ 13 ⫽ 21.

⫽ 3 ⫹ 5 ⫽ 8, c

⫽ 5 ⫹ 8 ⫽ 13,

⫽ 5 ⫽ 3 ⫽ 2

⫽ 3 ⫹ 2 ⫽ 2 ⫹ 1 ⫽ 1 ⫹ 1

⫽ c

⫹ c

⫽ c

⫹ c

⫽ c

⫹ c

⫽ c

5⫺1

⫹ c

5⫺2

⫽ c

4⫺1

⫹ c

4⫺2

⫽ c

3⫺1

⫹ c

3⫺2

n ⫽ 3.

⫽ c

n⫺1

⫹ c

n⫺2

⫽ 1, c

⫽ 1

2nd

STO

u1n2⫽ 1⫺12

764 CHAPTER 9 Additional Topics in Algebra 9–4

College Algebra Graphs & Models—

WORTHY OF NOTE

One application of the Fibonacci

sequence involves the Fibonacci

spiral, found in the growth of many

ferns and the spiral shell of many

mollusks.

Figure 9.7

Figure 9.8

Figure 9.5Figure 9.6

A. You’ve just seen how

we can write out the terms of

a sequence given the general

or nth term

cob19545_ch09_761-773.qxd 12/17/10 12:44 AM Page 764

9–5 Section 9.1 Sequences and Series 765

College Algebra Graphs & Models—

Rewriting a factorial in equivalent forms often makes it easier to simplify certain

expressions. For example, we can rewrite 5! as or , and so on. Con-

sider Example 4.

EXAMPLE 4

䊳

Simplifying Expressions Using Factorial Notation

Simplify by writing the numerator in an equivalent form.

a. b. c.

Solution

䊳

a. b. c.

Now try Exercises 39 through 44

䊳

Most calculators have a factorial option or key. On many calculator models it is located

on a submenu of the key: PRB 4: !.

EXAMPLE 5

䊳

Computing a Speciﬁed Term from a Sequence Deﬁned Using Factorials

Find and simplify the third term of each sequence.

a. b.

Algebraic Solution

䊳

a. b.

Technology Solution

䊳

For this exercise we enter as u(n), and

as v(n). Once these functions

have been deﬁned on the screen, we can

evaluate them on the home screen as with

other functions (Figure 9.9), or use the

TABLE feature (Figure 9.10).

Now try Exercises 45 through 50

䊳

C. Series and Partial Sums

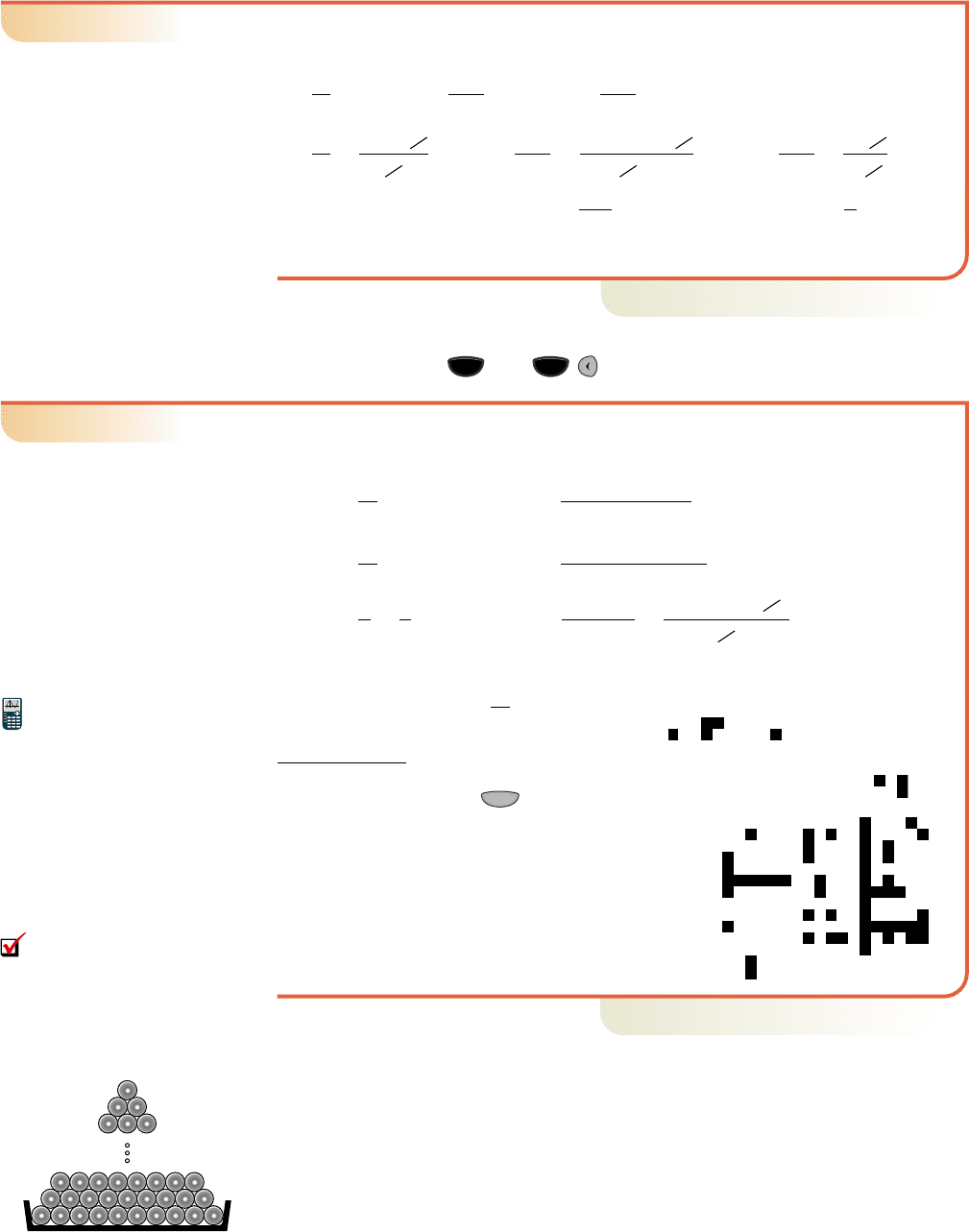
Sometimes the terms of a sequence are dictated by context rather than a formula. Con-

sider the stacking of large pipes in a storage yard. If there are 10 pipes in the bottom

row, then 9 pipes, then 8 (see Figure 9.11), how many pipes are in the stack if there is

a single pipe at the top? The sequence generated is 10, 9, 8, , 3, 2, 1 and to answer

the question we would have to compute the sum of all terms in the sequence. When the

terms of a ﬁnite sequence are added, the result is called a ﬁnite series.

1⫺12

12n ⫺ 12!

⫽⫺20

⫽

1⫺1215!2

⫽

1⫺1235

3!4

⫽

1⫺12

32132⫺ 14!

⫽

1⫺12

12n ⫺ 12!

⫽

MATHMATH

⫽ 1 ⫽ 495 ⫽ 72

⫽

990

⫽ 9

3!5!

⫽

3!5!

11!

8!2!

⫽

8!2!

⫽

3!5!

11!

8!2!

5! ⫽ 5

3!5

Figure 9.9, 9.10

B. You’ve just seen how

we can work with recursive

sequences and sequences

involving a factorial

Figure 9.11

cob19545_ch09_761-773.qxd 11/9/10 8:19 PM Page 765

766 CHAPTER 9 Additional Topics in Algebra 9–6

College Algebra Graphs & Models—

Finite Series

Given the sequence a

, a

, , a

, the sum of the terms is called a ﬁnite series

or partial sum and is denoted S

EXAMPLE 6

䊳

Computing a Partial Sum

Given ﬁnd the value of a. S

b. S

Solution

䊳

Since we eventually need the sum of the ﬁrst seven terms, begin by writing out

these terms: 2, 4, 6, 8, 10, 12, and 14.

a. b.

Now try Exercises 51 through 56

䊳

There are several ways of computing a partial

sum using technology, with the most common

being (1) storing the sequence in a list then com-

puting the sum of the list elements, or (2) computing

the sum of a sequence directly on the home screen

using the appropriate commands. On many calcu-

lators, the “sum(” option is in a MATH sub-

menu, accessed using (LIST)

(MATH) 5:sum(. For the sum in Example 6(b), we

have , with option (1) demonstrated in Figure 9.12 and option (2) in

Figure 9.13.

D. Summation Notation

When the general term of a sequence is known, the Greek letter sigma can be used to

write the related series as a formula. For instance, to indicate the sum of the ﬁrst four term

of we write with this notation indicating we are to compute

the sum of all terms generated as i cycles from 1 through 4. This result is called sum-

mation or sigma notation and the letter i is called the index of summation. The letters

j, k, l, and m are also used as index numbers, and the summation need not start at 1.

EXAMPLE 7

䊳

Computing a Partial Sum

Compute each sum:

a. b. c.

d. Check each sum using a graphing calculator.

Solution

䊳

⫽

⫹

⫽

137

兺

j⫽1

⫽

⫹

⫽ 5 ⫹ 8 ⫹ 11 ⫹ 14 ⫽ 38

兺

i⫽1

13i ⫹ 22⫽ 13

1 ⫹ 22⫹ 13

2 ⫹ 22⫹ 13

3 ⫹ 22⫹ 13

4 ⫹ 22

兺

k⫽3

1⫺12

兺

j⫽1

兺

i⫽1

13i ⫹ 22

兺

i⫽1

13i ⫹ 22a

⫽ 3n ⫹ 2,

u1n2⫽ 2n

STAT

2nd

⫽ 56 ⫽ 20

⫽ 2 ⫹ 4 ⫹ 6 ⫹ 8 ⫹ 10 ⫹ 12 ⫹ 14 ⫽ 2 ⫹ 4 ⫹ 6 ⫹ 8

⫽ a

⫹ a

⫽ a

⫹ a

⫽ 2n,

⫽ a

⫹ a

⫹

⫹ a

n⫺1

⫹ a

Figure 9.12

Figure 9.13

C. You’ve just seen how

we can ﬁnd the partial sum

of a series

cob19545_ch09_761-773.qxd 11/9/10 8:19 PM Page 766

9–7 Section 9.1 Sequences and Series 767

College Algebra Graphs & Models—

d. Begin by entering the functions in parts (a), (b), and (c) as u(n), v(n), and w(n)

respectively on the screen (Figure 9.14). Note that while different indices

are used in this example, all are entered into the calculator using the variable n.

The results are shown in Figures 9.15 and 9.16.

⫽⫺9 ⫹ 16 ⫹ 1⫺252⫹ 36 ⫽ 18

兺

k⫽3

1⫺12

⫽ 1⫺12

⫹ 1⫺12

Figure 9.14

Figure 9.15

Figure 9.16

Now try Exercises 57 through 68

䊳

If a deﬁnite pattern is noted in a given series expansion, this process can be

reversed, with the expanded form being expressed in summation notation using the

nth term.

EXAMPLE 8

䊳

Writing a Sum in Sigma Notation

Write each of the following sums in summation (sigma) notation.

a. b.

Solution

䊳

a. The series has ﬁve terms and each term is an odd number, or 1 less than a

multiple of 2. The general term is and the series is

b. The raised ellipsis “ ” indicates the sum continues inﬁnitely. Since the terms

are multiples of 3, we identify the general term as , while noting the

series starts at (instead of ). Since the sum continues indeﬁnitely,

we use the inﬁnity symbol as the “ending” value in sigma notation. The

series is

Now try Exercises 69 through 78

䊳

Since the commutative and associative laws hold for the addition of real numbers,

summations have the following properties:

Properties of Summation

Given any real number c and natural number n,

(I)

If you add a constant c “n” times the result is cn.

(II)

A constant can be factored out of a sum.

兺

i⫽1

⫽ c

兺

i⫽1

兺

i⫽1

c ⫽ cn

兺

n⫽2

3n.

n ⫽ 1n ⫽ 2

⫽ 3n

兺

n⫽1

12n ⫺ 12.a

⫽ 2n ⫺ 1,

6 ⫹ 9 ⫹ 12 ⫹ 15 ⫹

1 ⫹ 3 ⫹ 5 ⫹ 7 ⫹ 9

WORTHY OF NOTE

By varying the function given and/or

where the sum begins, more than

one acceptable form is possible.

For Example 8(b)

also works.

兺

k⫽1

13 ⫹ 3k2

cob19545_ch09_761-773.qxd 11/9/10 8:19 PM Page 767

(III)

A summation can be distributed to two (or more) sequences.

(IV)

A summation is cumulative and can be written as a sum of smaller parts.

The veriﬁcation of property II depends solely on the distributive property.

Proof: expand sum

factor out c

write series in summation form

The veriﬁcations of properties III and IV simply use the commutative and associa-

tive properties. You are asked to prove property III in Exercise 94.

EXAMPLE 9

䊳

Computing a Sum Using Summation Properties

Recompute the sum from Example 7(a) using summation properties.

Solution

䊳

property III

property II

1 ⫹ 2 ⫹ 3 ⫹ 4 ⫽ 10; property I

result

Now try Exercises 79 through 82

䊳

E. Applications of Sequences

To solve applications of sequences, (1) identify where the sequence begins (the initial

term), (2) write out the ﬁrst few terms to help identify the nth term, and (3) decide on

an appropriate approach or strategy.

EXAMPLE 10

䊳

Solving an Application—Accumulation of Stock

Hydra already owned 1420 shares of stock when her company began offering

employees the opportunity to purchase 175 discounted shares per year. If she made

no purchases other than these discounted shares each year, how many shares will

she have 9 yr later? If this continued for the 25 yr she will work for the company,

how many shares will she have at retirement?

Solution

䊳

To begin, it helps to simply write out the ﬁrst few terms of the sequence. Since she

already had 1420 shares before the company made this offer, we let be

the inaugural element, showing (after 1 yr, she owns

1595 shares). The ﬁrst few terms are 1595, 1770, 1945, 2120, and so on. This

supports a general term of a

⫽ 1595 ⫹ 1751n ⫺ 12.

1420 ⫹ 175 ⫽a

⫽ 1595

⫽ 1420

⫽ 38

⫽ 31102⫹ 2142

⫽ 3

兺

i⫽1

i ⫹

兺

i⫽1

兺

i⫽1

13i ⫹ 22⫽

兺

i⫽1

3i ⫹

兺

i⫽1

兺

i⫽1

13i ⫹ 22

⫽ c

兺

i⫽1

⫽ c1a

⫹ a

⫹

⫹ a

兺

i⫽1

⫽ ca

⫹ ca

⫹

⫹ ca

兺

i⫽1

⫹

兺

i⫽m⫹1

⫽

兺

i⫽1

; 1 ⱕ m 6 n

兺

i⫽1

⫾ b

2⫽

兺

i⫽1

⫾

兺

i⫽1

768 CHAPTER 9 Additional Topics in Algebra 9–8

College Algebra Graphs & Models—

D. You’ve just seen how

we can use summation

notation to write and

evaluate series

cob19545_ch09_761-773.qxd 11/10/10 9:09 PM Page 768

After 9 years After 25 years

After 9 yr she would have 2995 shares. Upon retirement she would own 5795

shares of company stock.

Now try Exercises 85 through 90

䊳

Surprisingly, sequences and series have a number of other interesting properties,

applications, and mathematical connections. For instance, some of the most celebrated

numbers in mathematics can be approximated using a series, as demonstrated in

Example 11.

EXAMPLE 11

䊳

Use a calculator to ﬁnd the partial sums S

, S

, and S

for the sequences given. If

any sum seems to be approaching a ﬁxed number, name that number.

a. b.

Solution

䊳

a. Begin by entering as u(n) on the screen. Using the “sum(” and “seq(”

commands as before produces the results shown in Figures 9.17 through 9.19,

where it appears the sum becomes very close to for larger values of n.e ⫺ 1

⫽

⫽ 5795 ⫽ 2995

⫽ 1595 ⫹ 1751242 a

⫽ 1595 ⫹ 175182

9–9 Section 9.1 Sequences and Series 769

College Algebra Graphs & Models—

Figure 9.17

Figure 9.18

Figure 9.19

b. After entering as v(n) on the screen, we once again compute the sums

indicated as shown in Figures 9.20 through 9.22. It appears the sum becomes

very close to for larger values of n.

Now try Exercises 91 and 92

䊳

Figure 9.20

Figure 9.21

Figure 9.22

E. You’ve just seen how

we can use sequences to

solve applications

cob19545_ch09_761-773.qxd 11/9/10 8:20 PM Page 769