Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.


EXAMPLE 8
䊳
Applying the Properties of a Hyperbola—The Location of a Storm
Two amateur meteorologists, living 4 km
apart (4000 m), see a storm approaching. The
one farthest from the storm hears a loud clap
of thunder 9 sec after the one nearest.
Assuming the speed of sound is 340 m/sec,
determine an equation that models possible
locations for the storm at this time.
Solution
䊳
Let M
1
represent the meteorologist nearest
the storm and M
2
the farthest. Since M
2
heard
the thunder 9 sec after M
1
, M
2
must be
m farther away from the
storm S. In other words, from our definition
of a hyperbola, we have
The set of all points that satisfy this equation
will be on the graph of a hyperbola, and we’ll
use this fact to develop an equation model for
possible locations of the storm. Let’s place
the information on a coordinate grid. For
convenience, we’ll use the straight
line distance between M
1
and M
2
as
the x-axis, with the origin an equal
distance from each. With the
constant difference equal to 3060,
we have from
the definition of a hyperbola, giving
. With
(the distance from the origin to M
1
or M
2
), we find the value of b using
the equation or
The equation that models possible
locations of the storm is .
Now try Exercises 85 and 86
䊳
x
2
1530
2
y
2
1288
2
⬇ 1
1,659,100 ⬇ 1288
2
.b
2
120002
2
115302
2
c
2
a
2
b
2
: 2000
2
1530
2
b
2
c 2000 m
x
2
1530
2
y
2
b
2
1
2a 3060, a 1530
冟
d
1
d
2
冟
3060.
9
#
340 3060
740 CHAPTER 8 Analytic Geometry and the Conic Sections 8–34
College Algebra G&M—
x
y
1
1
1
2
2
1 2 3 in 1000s23
M
2
M
1
S
D. You’ve just seen how
we can solve applications
involving foci
䊳
CONCEPTS AND VOCABULARY
Fill in the blank with the appropriate word or phrase. Carefully reread the section if needed.
8.3 EXERCISES
2. The center of a hyperbola is located
between the vertices.
1. The line that passes through the vertices of a
hyperbola is called the axis.
3. The conjugate axis is to the
axis and contains the
of the hyperbola.
4. The center of the hyperbola defined by
is at .
1x 22
2
4
2
1y 32
2
5
2
1
cob19545_ch08_731-745.qxd 12/15/10 10:57 AM Page 740

5. Compare/Contrast the two methods used to find the
asymptotes of a hyperbola. Include an example
illustrating both methods.
6. Explore/Explain why
results in a hyperbola regardless of
whether or Illustrate with an
example.
A B.A B
1A, B 7 02
A1x h2
2
B1y k2
2
F,
䊳
DEVELOPING YOUR SKILLS
Graph each hyperbola. Label the center, vertices, and
any additional points used.
7. 8.
9. 10.
11. 12.
13. 14.
15. 16.
17. 18.
19. 20.
21. 22.
For the graphs given, state the location of the vertices
and the equation of the transverse axis. Then identify
the location of the center and the equation of the
conjugate axis. Note the scale used on each axis.
23. 24.
25. 26.
x
y
1010
10
10
x
y
1010
10
10
x
y
1010
10
10
x
y
1010
10
10
y
2
16
x
2
4
1
y
2
36
x
2
25
1
y
2
4
x
2
4
1
y
2
9
x
2
9
1
y
2
9
x
2
18
1
y
2
12
x
2
4
1
y
2
1
x
2
4
1
y
2
9
x
2
1
1
x
2
81
y
2
16
1
x
2
36
y
2
16
1
x
2
25
y
2
9
1
x
2
49
y
2
16
1
x
2
25
y
2
16
1
x
2
4
y
2
9
1
x
2
16
y
2
9
1
x
2
9
y
2
4
1
Sketch a complete graph of each equation, including the
asymptotes. Be sure to identify the center and vertices.
27. 28.
29.
30.
31.
32.
33.
34.
35.
36.
37.
38.
39. 40.
41. 42.
43. 44.
Graph each hyperbola by writing the equation in
standard form. Label the center and vertices, and sketch
the asymptotes. Then use a graphing calculator to graph
each relation and locate four additional points whose
coordinates are rational.
45.
46.
47.
48.
Classify each equation as that of a circle, ellipse, or
hyperbola. Justify your response (assume all are
nondegenerate).
49.
50. 9y
2
4x
2
36
4x
2
4y
2
24
9x
2
4y
2
18x 24y 9 0
4y
2
x
2
24y 4x 28 0
x
2
4y
2
12x 16y 16 0
4x
2
y
2
40x 4y 60 0
36x
2
20y
2
18012x
2
9y
2
72
25y
2
4x
2
1009y
2
4x
2
36
16x
2
25y
2
40016x
2
9y
2
144
81x 42
2
31y 32
2
24
121x 42
2
51y 32
2
60
91y 42
2
51x 32
2
45
21y 32
2
51x 12
2
50
91x 12
2
1y 32
2
81
1x 22
2
41y 12
2
16
1y 32
2
16
1x 22
2
5
1
1y 12
2
7
1x 52
2
9
1
1x 22
2
9
1y 12
2
4
1
1x 32
2
36
1y 22
2
49
1
y
2
4
1x 22
2
9
1
1y 12
2
4
x
2
25
1
8–35 Section 8.3 The Hyperbola 741
College Algebra G&M—
cob19545_ch08_731-745.qxd 10/25/10 2:51 PM Page 741
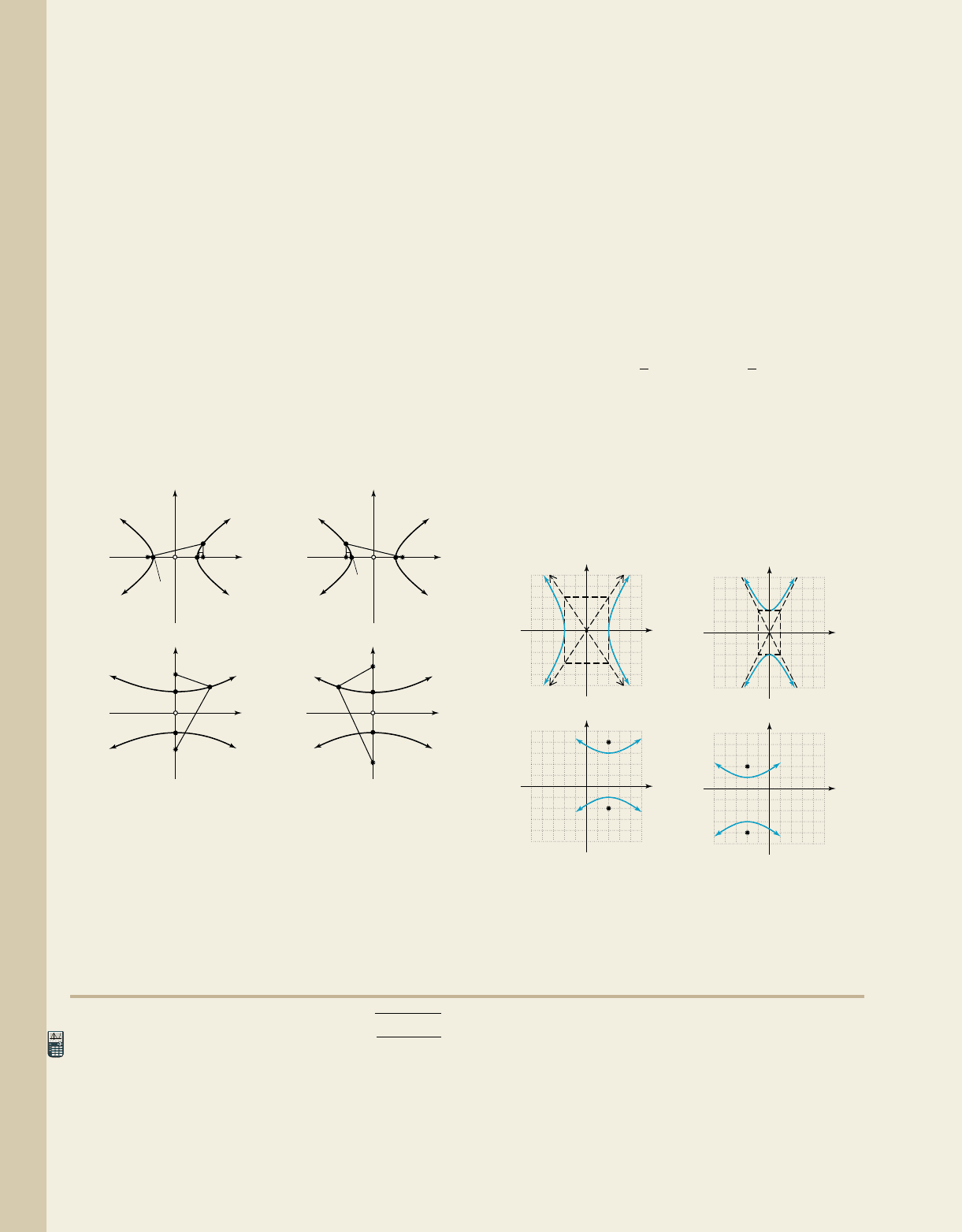
51.
52.
53.
54.
55.
56.
57.
58.
59.
60.
Use the definition of a hyperbola to find the distance
between the vertices and the dimensions of the rectangle
centered at (h, k). Figures are not drawn to scale. Note
that Exercises 63 and 64 are vertical hyperbolas.
61. 62.
63. 64.
Write each equation in standard form to find and list
the coordinates of the (a) center, (b) vertices, (c) foci,
and (d) dimensions of the central rectangle. Then
(e) sketch the graph, including the asymptotes.
65.
66. 4x
2
36y
2
40x 144y 188 0
4x
2
9y
2
24x 72y 144 0
x
y
(0, b)
(9, 6.25)
(0, b)
(0, 13)
(0, 13)
x
y
(0, 10)
(6, 7.5)
(0, 10)
(0, b)
(0, b)
y
x
(15, 0)
(15, 0)
(a, 0)
(a, 0)
(15, 6.75)
y
x
(5, 0)
(5, 0)
(a, 0)
(a, 0)
(5, 2.25)
9x
2
9y
2
9x 12y 4 0
16x
2
5y
2
3x 4y 538
2y
2
3 6x
2
8
2x
2
2y
2
x 20
x y
2
3x
2
9
x
2
5 2y
2
36x
2
25y
2
900
2x
2
4y
2
8
x
2
y
2
6y 7
x
2
y
2
2x 4y 4 67.
68.
69.
70.
Find the equation of the hyperbola (in standard form)
that satisfies the following conditions:
71. vertices at ( ) and (6, 0); foci at ( ) and
(8, 0)
72. vertices at ( ) and (4, 0); foci at ( ) and
(6, 0)
73. foci at and length of
conjugate axis: 6 units
74. foci at ( ) and (7, 2); length of conjugate axis:
8 units
Use the characteristics of a hyperbola and the graph
given to write the related equation and state the location
of the foci (75 and 76) or the dimensions of the central
rectangle (77 and 78).
75. 76.
77. 78.
2
2
4
6
8
10
4
6
8
10
y
864210864210
x
5432154321
1
2
3
4
5
2
3
4
1
5
y
x
2
2
4
6
8
10
4
6
8
10
y
864210864210
x
5432154321
1
2
3
4
5
2
3
4
1
5
y
x
5, 2
12, 312
2;12, 3122
6, 04, 0
8, 06, 0
10x
2
60x 5y
2
20y 20 0
9x
2
3y
2
54x 12y 33 0
4y
2
81x
2
162x 405 0
4y
2
16x
2
24y 28 0
742 CHAPTER 8 Analytic Geometry and the Conic Sections 8–36
College Algebra G&M—
䊳
WORKING WITH FORMULAS
79. Equation of a semi-hyperbola:
The “upper half” of a certain hyperbola is given by the equation shown. (a) Simplify the radicand, (b) state the
domain of the expression, and (c) enter the expression as Y
1
on a graphing calculator and graph. What is the
equation for the “lower half” of this hyperbola?
y ⴝ
B
36 ⴚ 4x
2
ⴚ9
cob19545_ch08_731-745.qxd 10/25/10 2:52 PM Page 742

8–37 Section 8.3 The Hyperbola 743
College Algebra G&M—
䊳
APPLICATIONS
81. Stunt pilots:At an air show, a stunt plane dives along
a hyperbolic path whose vertex is directly over the
grandstands. If the plane’s flight path can be modeled
by the hyperbola what is
the minimum altitude of the plane as it passes over
the stands? Assume x and y are in yards.
82. Flying clubs: To test their skill as pilots, the members
of a flight club attempt to drop sandbags on a target
placed in an open field, by diving along a hyperbolic
path whose vertex is directly over the target area. If
the flight path of the plane flown by the club’s
president is modeled by what
is the minimum altitude of her plane as it passes over
the target? Assume x and y are in feet.
83. Charged particles: It has been shown that when
like particles with a common charge are hurled at
each other, they deflect and travel along paths that
are hyperbolic. Suppose the paths of two such
particles is modeled by the hyperbola
. What is the minimum distance
between the particles as they approach each other?
Assume x and y are in microns.
84. Nuclear cooling towers: The natural draft cooling
towers for nuclear power stations are called
hyperboloids of one sheet. The perpendicular cross
sections of these hyperboloids form two branches
of a hyperbola. Suppose the central cross section of
one such tower is modeled by the hyperbola
. What is the
minimum distance between the sides of the tower?
Assume x and y are in feet.
1600x
2
4001y 502
2
640,000
x
2
9y
2
36
9y
2
16x
2
14,400,
25y
2
1600x
2
40,000,
85. Locating a ship using radar: Under certain
conditions, the properties of a hyperbola can be
used to help locate the position of a ship. Suppose
two radio stations are located 100 km apart along a
straight shoreline. A ship is sailing parallel to the
shore and is 60 km out to sea. The ship sends out a
distress call that is picked up by the closer station
in 0.4 milliseconds (msec—one-thousandth of a
second), while it takes 0.5 msec to reach the station
that is farther away. Radio waves travel at a speed
of approximately 300 km/msec. Use this
information to find the equation of a hyperbola that
will help you find the location of the ship, then find
the coordinates of the ship. (Hint: Draw the
hyperbola on a coordinate system with the radio
stations on the x-axis at the foci, then use the
definition of a hyperbola.)
86. Locating a plane using radar: Two radio stations
are located 80 km apart along a straight shoreline,
when a “mayday” call (a plea for immediate help)
is received from a plane that is about to ditch in the
ocean (attempt a water landing). The plane was
flying at low altitude, parallel to the shoreline, and
20 km out when it ran into trouble. The plane’s
distress call is picked up by the closer station in
0.1 msec, while it takes 0.3 msec to reach the other.
Use this information to construct the equation of a
hyperbola that will help you find the location of the
ditched plane, then find the coordinates of the
plane. Also see Exercise 85.
80. Focal chord of a hyperbola:
The focal chords of a hyperbola are line segments parallel to the conjugate axis with
endpoints on the hyperbola, and containing points f
1
and f
2
(see grid). The length of the
chord is given by the formula shown, where n is the distance from center to vertex and m is
the distance from center to one side of the central rectangle. Use the formula to find the
length of the focal chord for the hyperbola indicated, then compare the calculated value with
the length estimated from the given graph:
.
1x 22
2
4
1y 12
2
5
1
L ⴝ
2m
2
n
x
y
f
1
f
2
108642108642
2
4
6
8
10
4
6
8
10
2
cob19545_ch08_731-745.qxd 10/25/10 2:52 PM Page 743

744 CHAPTER 8 Analytic Geometry and the Conic Sections 8–38
College Algebra G&M—
䊳
EXTENDING THE CONCEPT
87. For a greater understanding as to why the branches
of a hyperbola are asymptotic, solve
for y, then consider what happens as (note
that for large x).x
2
k ⬇ x
2
x Sq
x
2
a
2
y
2
b
2
1
88. Which has a greater area: (a) The central rectangle of
the hyperbola given by ,
(b) the circle given by ,
or (c) the ellipse given by
?91x 52
2
101y 42
2
570
1x 52
2
1y 42
2
57
1x 52
2
1y 42
2
57
89. It is possible for the plane to intersect only the vertex of the cone or to be tangent to the sides. These are called
degenerate cases of a conic section. Many times we’re unable to tell if the equation represents a degenerate case
until it’s written in standard form. Write the following equations in standard form and comment.
a. b. x
2
4x 5y
2
40y 84 04x
2
32x y
2
4y 60 0
䊳
MAINTAINING YOUR SKILLS
90. (2.5) Graph the piecewise-defined function:
91. (4.1) Use synthetic division and the remainder
theorem to determine if is a zero of
If
yes, find its multiplicity.
92. (4.2) The number is a solution to two
out of the three equations given. Which two?
a.
b.
c. x
2
2x 3 0
x
3
6x
2
11x 12 0
x
4
4 0
z 1 i12
g1x2 x
5
5x
4
4x
3
16x
2
32x 16.
x 2
f 1x2 e
4 x
2
2 x 6 3
5 x 3
93. (6.4) A government-approved company is licensed
to haul toxic waste. Each container of solid waste
weighs 800 lb and has a volume of 100 ft
3
. Each
container of liquid waste weighs 1000 lb and is
60 ft
3
in volume. The revenue from hauling solid
waste is $300 per container, while the revenue from
liquid waste is $350 per container. The truck used by
this company has a weight capacity of 39.8 tons and
a volume capacity of 6960 ft
3
. What combination of
solid and liquid waste containers will produce the
maximum revenue?
8.4 The Analytic Parabola; More on Nonlinear Systems
In previous coursework, you likely learned that the
graph of a quadratic function was a parabola. Parabolas
are actually the fourth and final member of the family
of conic sections, and as we saw in Section 8.1, the
graph can be obtained by observing the intersection of
a plane and a cone. If the plane is parallel to the gener-
ator of the cone (shown as a dark line in Figure 8.36), the intersection of the plane with
one nappe forms a parabola. In this section we develop the general equation of a
parabola from its analytic definition, opening a new realm of applications that extends
far beyond those involving only zeroes and extreme values.
A. Parabolas with a Horizontal Axis
An introductory study of parabolas generally involves those with a vertical axis, de-
fined by the equation Unlike the previous conic sections, this equa-
tion has only one second-degree (squared) term in x and defines a function. As a
y ax
2
bx c.
LEARNING OBJECTIVES
In Section 8.4 you will see
how we can:
A. Graph parabolas with a
horizontal axis of
symmetry
B. Identify and use the
focus-directrix form of
the equation of a
parabola
C. Solve nonlinear systems
involving the conic
sections
D. Solve applications of the
analytic parabola
Axis
Element
Parabola
Figure 8.36
cob19545_ch08_731-745.qxd 12/15/10 10:58 AM Page 744

8–39 Section 8.4 The Analytic Parabola; More on Nonlinear Systems 745
College Algebra G&M—
review, the primary characteristics are listed here and illustrated in Figure 8.37. See
Exercises 7 through 12.
Vertical Parabolas
For a second-degree equation of the form , the graph is a vertical
parabola with these characteristics:
1. opens upward if downward if
2. y-intercept: (0, c) (substitute 0 for x)
3. x-intercept(s): substitute 0 for y and solve.
4. axis of symmetry:
5. vertex:
Horizontal Parabolas
Similar to our study of horizontal and vertical hyperbolas, the graph of a parabola can
open to the right or left, as well as up or down. After interchanging the variables x and
y in the standard equation, we obtain the parabola noting the result-
ing graph will be a reflection about the line Here, the axis of symmetry is a hor-
izontal line and factoring or the quadratic formula is used to find the y-intercepts (if they
exist). Note that although the graph is still a parabola—it is not the graph of a function.
Horizontal Parabolas
For a second-degree equation of the form the graph is a
horizontal parabola with these characteristics:
1. opens right if left if
2. x-intercept: (c, 0) (substitute 0 for y)
3. y-intercepts(s): substitute 0 for x and solve.
4. axis of symmetry:
5. vertex:
EXAMPLE 1
䊳
Graphing a Horizontal Parabola
Graph the relation whose equation is then state the domain and
range of the relation.
Solution
䊳
Since the equation has a single squared term in
y, the graph will be a horizontal parabola. With
the parabola opens to the right.
The x-intercept is Factoring shows the
y-intercepts are and The axis of
symmetry is and substituting
this value into the original equation gives
The coordinates of the vertex are
Using horizontal and vertical
boundary lines we find the domain for this
relation is and the range is The graph is shown.
Now try Exercises 13 through 18
䊳
y 僆 1q, q2.x 僆 36.25, q2
16.25, 1.52.
x 6.25.
y
3
2
1.5,
y 1.y 4
14, 02.
a 7 0 1a 12,
x y
2
3y 4,
a
4ac b
2
4a
,
b
2a
b
y
b
2a
a 6 0.a 7 0,
x ay
2
by c,
y x.
x ay
2
by c,
1h,
k2 a
b
2a
,
4ac b
2
4a
b
x
b
2a
a 6 0.a 7 0,
y ax
2
bx c
1. Opens upward
2. y-intercept
4. Axis of symmetry
3. x-intercepts
5. Vertex
y
x
Figure 8.37
10 10
x
(0, 1)
y 1.5
(4, 0)
(0, 4)
(6.25, 1.5)
y
10
10
cob19545_ch08_731-745.qxd 10/25/10 2:52 PM Page 745

As with the vertical parabola, the equation of a horizontal parabola can be written
as a transformation: by completing the square. Note that in this
case, the vertical shift is k units opposite the sign, with a horizontal shift of h units in
the same direction as the sign.
EXAMPLE 2
䊳
Graphing a Horizontal Parabola by Completing the Square
Graph by completing the square: , then state the domain and range.
Solution
䊳
Using the original equation, we note the
graph will be a horizontal parabola opening to
the left and have an x-intercept of
Completing the square gives
so the equation
of this parabola in shifted form is
The vertex is at and is the axis of
symmetry. This means there are no y-intercepts, a
fact that comes to light when we attempt to solve
the equation after substituting 0 for x:
substitute 0 for
x
no real roots
Using symmetry, the point is also on the graph. After plotting these
points we obtain the graph shown. From the graph, the domain is
and the range is .
Now try Exercises 19 through 36
䊳
As with the other relations graphed in this chapter, a horizontal parabola also fails
the vertical line test and we must graph the relation in two pieces. Using the equation
from Example 2 we have
shifted form
isolate
y
-term
divide by 2
take square roots
solve for
y
The graph is given in Figure 8.38, and shows that (3, 1) is also a point on the graph.
B. The Focus-Directrix Form of the Equation of a Parabola
As with the ellipse and hyperbola, many significant applications of the parabola rely on
its analytical definition rather than its algebraic form. From the construction of radio
telescopes to the manufacture of flashlights, the location of the focus of a parabola is
Y
1
2
B
X 1
2
, Y
2
2
B
X 1
2
2
B
x 1
2
y
B
x 1
2
y 2
x 1
2
1y 22
2
x 1 21y 22
2
x 21y 22
2
1
y 僆 ⺢
x 僆 1q,
14
19, 42
1y 22
2
1
2
21y 22
2
1 0
y 211, 22
x 21y 22
2
1
x 21y
2
4y 42 9 8,
19, 02.
1a 22
x2y
2
8y 9
x a1y k2
2
h
746 CHAPTER 8 Analytic Geometry and the Conic Sections 8–40
College Algebra G&M—
(0, 1)
(1, 2)
(9, 0)
(9, 4)
x
y
1010
10
x
y
y 2
13.4 5.4
8.2
4.2
Figure 8.38
A. You’ve just seen how
we can graph parabolas with a
horizontal axis of symmetry
cob19545_ch08_746-754.qxd 10/25/10 2:55 PM Page 746
critical. To understand these and other applications, we use the analytic definition of a
parabola first introduced in Section 8.1.
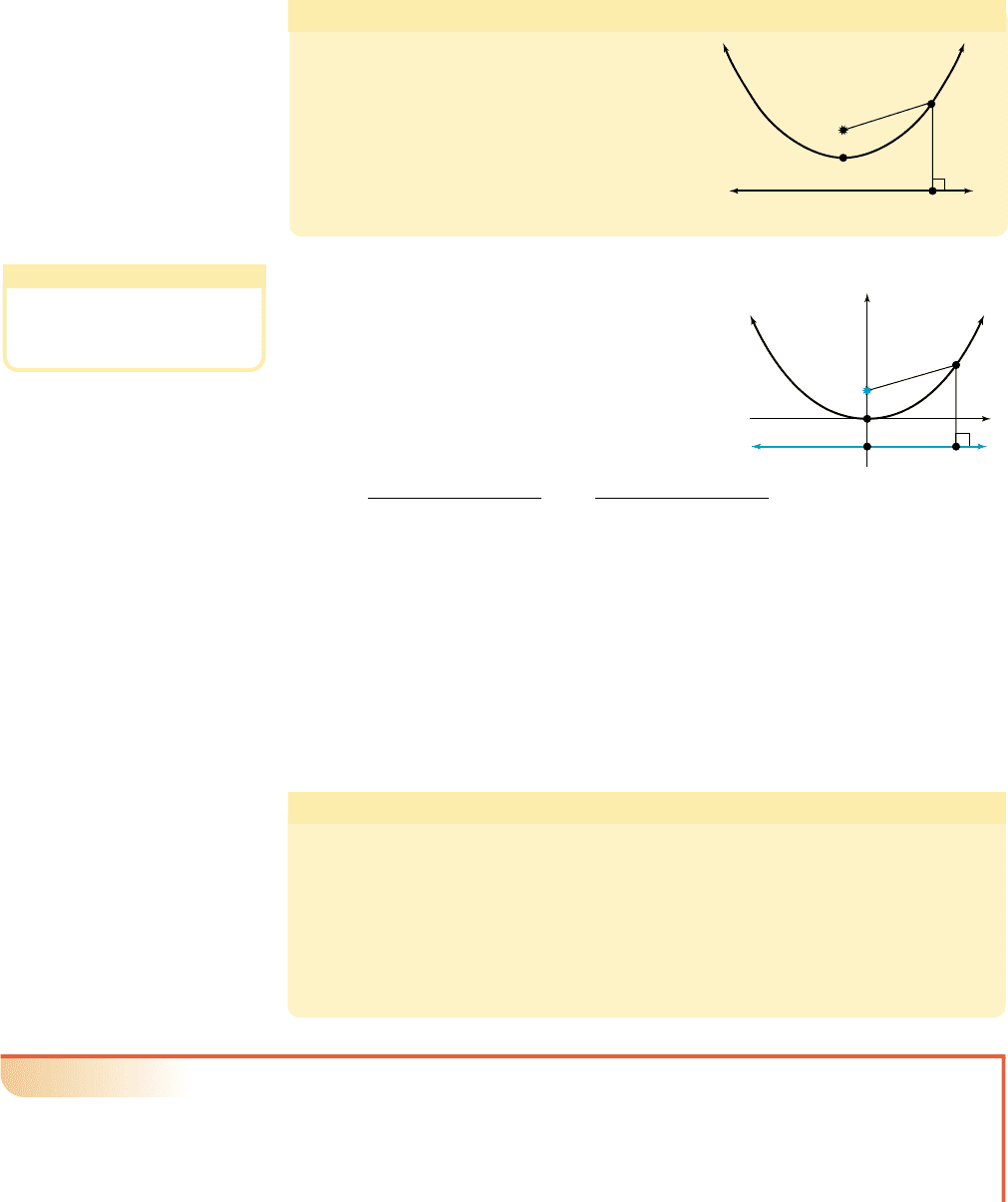
Definition of a Parabola
Given a fixed point f and fixed line D in the plane,
a parabola is the set of all points (x,y) such that the
distance from f to (x, y) is equal to the distance
from line D to (x, y). The fixed point f is the focus
of the parabola, and the fixed line is the directrix.
The general equation of a parabola can be
obtained by combining this definition with the dis-
tance formula. With no loss of generality, we can
assume the parabola shown in the definition box is
oriented in the plane with the vertex at (0, 0) and
the focus at (0, p). As the diagram in Figure 8.39
indicates, this gives the directrix an equation of
with all points on D having coordinates of
Using the distance formula yields
from the definition
square both sides
simplify; expand binomials
subtract
p
2
and
y
2
isolate
x
2
The resulting equation is called the focus-directrix form of a vertical parabola
with center at (0, 0). If we had begun by orienting the parabola so it opened to the right,
we would have obtained the equation of a horizontal parabola with center (0, 0):
The Equation of a Parabola in Focus-Directrix Form
Vertical Parabola Horizontal Parabola
focus (0, p), directrix: focus at (p, 0), directrix:
If opens upward. If opens to the right.
If opens downward. If opens to the left.
For a parabola, note there is only one second-degree term.
EXAMPLE 3
䊳
Locating the Focus and Directrix of a Parabola
Find the vertex, focus, and directrix for the parabola defined by Then
sketch the graph, including the focus and directrix.
Solution
䊳
Since the x-term is squared and no shifts have been applied, the graph will be a
vertical parabola with a vertex of (0, 0). Use a direct comparison between the given
x
2
12y.
p 6 0,p 6 0,
p 7 0,p 7 0,
x py p
y
2
4pxx
2
4py
y
2
4px.
x
2
4py
x
2
2py 2py
x
2
y
2
2py p
2
0 y
2
2py p
2
1x 02
2
1y p2
2
1x x2
2
1y p2
2
21x 02
2
1y p2
2
21x x2
2
1y p2
2
d
1
d
2
1x, p2.
y p
8–41 Section 8.4 The Analytic Parabola; More on Nonlinear Systems 747
College Algebra G&M—
D
f
Vertex
(x, y)
d
1
d
1
d
2
d
2
D
P(x, y)
y p
(0, p)
(0, p)(x, p)
F
(0, 0)
x
y
d
1
d
2
Figure 8.39
WORTHY OF NOTE
For the analytic parabola, we use p
to designate the focus since c is so
commonly used as the constant
term in .y ax
2
bx c
cob19545_ch08_746-754.qxd 10/25/10 9:37 PM Page 747

equation and the focus-directrix form to determine the value of p:
given equation
focus-directrix form
This shows:
Since the parabola opens downward, with the focus at
and directrix To complete the graph we need a few additional points. Since
36 is divisible by 12, we can use inputs of and
giving the points and Note the axis of symmetry is The
graph is shown.
Now try Exercises 37 through 48
䊳
As an alternative to calculating additional points to sketch the graph, we can use what
is called the focal chord of the parabola. Similar to the ellipse and hyperbola, the focal
chord is the line segment that contains the focus, is parallel to the directrix, and has its end-
points on the graph. Using the definition of a parabola and the diagram in Figure 8.40, we
note the vertical distance from (x, y) to the directrix is 2p. Since a line
segment parallel to the directrix from the focus to the graph will also have a length of
and the focal chord of any parabola has a total length of Note that in Example 3, the
points we happened to choose were actually the endpoints of the focal chord.
Finally, if the vertex of a vertical parabola is shifted to (h, k), the equation will have
the form As with the other conic sections, both the horizontal
and vertical shifts are “opposite the sign.”
EXAMPLE 4
䊳
Locating the Focus and Directrix of a Parabola
Find the vertex, focus, and directrix for the parabola whose equation is given,
then sketch the graph, including the focus, focal chord, and directrix:
Solution
䊳
Since only the x-term is squared, the graph will be a vertical parabola. To find the
end-behavior, vertex, focus, and directrix, we complete the square in x and use a
direct comparison between the shifted form and the focus-directrix form:
given equation
complete the square in
x
add 9
factor
Notice the parabola has been shifted 3 units right and 2 up, so all features of the
parabola will likewise be shifted. Since we have (the coefficient of the
linear term), we know and the parabola opens downward. If the
parabola were in standard position, the vertex would be at (0, 0), the focus at (0, )
and the directrix a horizontal line at But since the parabola is shifted 3 right
and 2 up, we add 3 to all x-values and 2 to all y-values to locate the features of the
shifted parabola. The vertex is at The focus is
and the directrix is Finally, the
horizontal distance from the focus to the graph is units (since ),
giving us the additional points and as endpoints of the focal
chord. The graph is shown.
Now try Exercises 49 through 60
䊳
19, 1213, 12
冟
4p
冟
12
冟
2p
冟
6
y 3 2 5.10 3, 3 22 13, 12
10 3, 0 22 13, 22.
y 3.
3
p 3 1p 6 02
4p 12
1x 32
2
121y 22
x
2
6x 9 12y 24
x
2
6x
___
12y 15
x
2
6x 12y 15 0
x
2
6x 12y 15 0.
1x h2
2
4p1y k2.
冟
4p
冟
.
冟
2p
冟
,
d
1
d
2
y p
x 0.16, 32.16, 32
3162
2
6
2
364,x 6x 6
y 3.
10, 32p 3 1p 6 02,
p 3
4 p 12
x
2
4py
T
x
2
12y
748 CHAPTER 8 Analytic Geometry and the Conic Sections 8–42
College Algebra G&M—
Figure 8.40
x
y
(0, 3)
(0, 0)
(6, 3)
(6, 3)
f
1010
10
10
x 0
y 3D
D
x
f
P
p
2p
y
p
Vertex
p
y
(x, y)
d
1
d
2
(3, 1)
(3, 1)
(9, 1)
(3, 2)
x
y
1010
10
10
x 3
y 5
cob19545_ch08_746-754.qxd 10/25/10 2:56 PM Page 748
In many cases, we need to construct the equation of the parabola when only
partial information in known, as illustrated in Example 5.
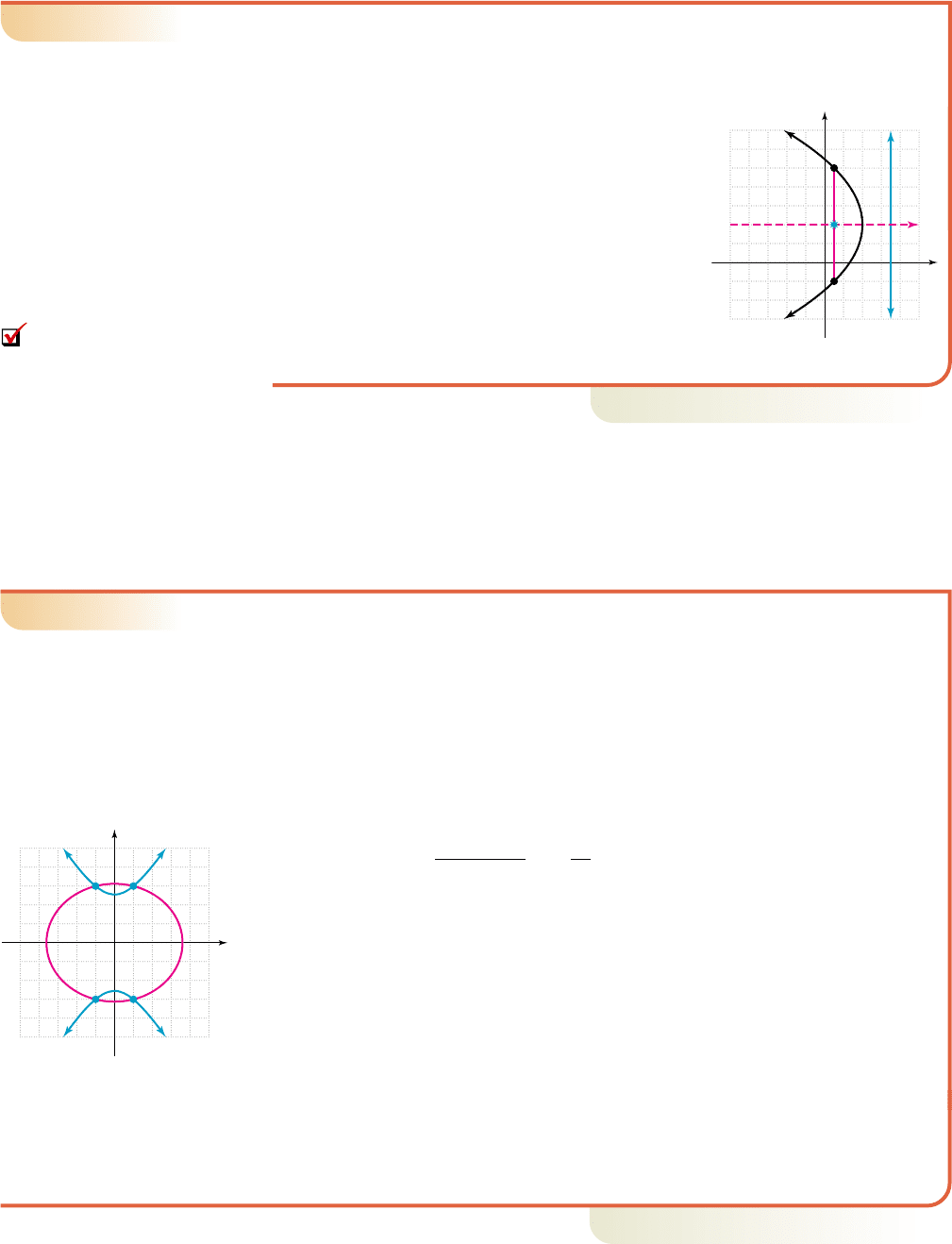
EXAMPLE 5
䊳
Constructing the Equation of a Parabola
Find the equation of the parabola with vertex (4, 4) and focus (1, 4). Then graph
the parabola using the equation and focal chord.
Solution
䊳
As the vertex and focus are on a horizontal line, we
have a horizontal parabola with general equation
. The distance p from vertex to
focus is 3 units, and with the focus to the left of the
vertex, the parabola opens left so . Using the
focal chord, the vertical distance from (1, 4) to the
graph is , giving points (1, 10)
and (1, 2). The vertex is shifted 4 units right
and 4 units up from (0, 0), showing and
, and the equation of the parabola must be
, with directrix . The graph
is shown.
Now try Exercises 61 through 76
䊳
C. Nonlinear Systems and the Conic Sections
Similar to our work with nonlinear systems in Section 6.3, the graphing, substitution,
or elimination method can still be used when the system involves a conic section.
When both equations in the system have at least one second degree term, it is generally
easier to use the elimination method.
EXAMPLE 6
䊳
Solving a System of Nonlinear Equations
Solve the system using elimination:
Solution
䊳
The first equation represents a vertical and central hyperbola, while the second
represents a horizontal and central ellipse. After writing the system with the x- and
y-terms in the same order, we obtain . Using will
eliminate the y-term.
2R1
R2
sum
divide by 13
square root property
Substituting and into the second equation we obtain
Since and 1 each generated two outputs, there are a total of four ordered
pair solutions: (1, ), (1, 3), ( ), and ( , 3). The graph is shown and
supports our results.
Now try Exercises 77 through 82
䊳
11, 33
1
y 3
or
y 3y 3
or
y 3
y
2
9 y
2
9
4 y
2
36 4 y
2
36
3 4y
2
39 3 4y
2
39
3 112
2
4y
2
39 3 112
2
4y
2
39
x 1x 1
x 1
or
x 1
x
2
1
13x
2
0 13
3x
2
4y
2
39
10x
2
4y
2
26
2R1 R2e
5x
2
2y
2
13
3x
2
4y
2
39
e
2y
2
5x
2
13
3x
2
4y
2
39
x 71y 42
2
121x 42
k 4
h 4
冟
2p
冟
冟
2132
冟
6
p 3
1y k2
2
4p1x h2
8–43 Section 8.4 The Analytic Parabola; More on Nonlinear Systems 749
College Algebra G&M—
e
6
10
14
10
x
y
B. You’ve just seen how
we can identify and use the
focus-directrix form of the
equation of a parabola
55
5
5
x
y
5x
2
2y
2
13
3x
2
4y
2
39
(1, 3)
(1, 3) (1, 3)
(1, 3)
cob19545_ch08_746-754.qxd 10/25/10 9:48 PM Page 749
