Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.


80. Pricing pet care products:A metal shop that
manufactures pens for pet rabbits has collected
some data on sales and production over the past
8 weeks. The following table shows the supply and
demand data for these pens. Find the equilibrium
point (round to the nearest cent and whole cage).
590 CHAPTER 6 Systems of Equations and Inequalities 6–16
College Algebra G&M—
81. Tracking supply and demand—oil products:
The U.S. Bureau of Labor and Statistics tracks
important data from many different markets. In
May 2008, it collected the following supply-and-
demand data for refined gasoline. Data were
collected every Tuesday and Friday. Find the
equilibrium point, rounding your answer to the
nearest hundred thousand gallons and whole cent.
Average Price Quantity Demanded Available Inventory
(in U.S. dollars) ( gal) ( gal)
3.17 8.82 9.10
3.12 8.87 9.05
3.04 9.08 8.97
2.84 9.22 8.91
3.11 8.92 9.02
3.15 8.76 9.08
3.10 9.01 8.99
3.11 8.94 9.01
2.93 9.13 8.93
1 ⴛ 10
7
1 ⴛ 10
7
Average Price Quantity Demanded Available Inventory
(in U.S. dollars) (in millions) (in millions)
9.40 0.84 1.23
8.51 1.17 0.95
8.78 1.05 1.11
10.82 0.68 1.29
6.77 1.47 0.77
9.33 0.91 1.21
8.34 1.25 0.88
10.37 0.76 1.27
8.62 1.09 1.02
8.44 1.21 0.92
8.58 1.18 0.97
8.96 1.01 1.17
82. Tracking supply and demand—energy efficient
lightbulbs: The U.S. Bureau of Labor and
Statistics has collected the following supply and
demand data for the energy-efficient fluorescent
lightbulbs sold each month for the past year. Find
the equilibrium point, rounding your answer to the
nearest ten thousand lightbulbs and whole cent.
What is the yearly demand at the equilibrium
point?
Descriptive Translation
83. Important dates in U.S. history: If you sum the
year that the Declaration of Independence was
signed and the year that the Civil War ended, you
get 3641. There are 89 yr that separate the two
events. What year was the Declaration signed?
What year did the Civil War end?
84. Architectural
wonders: When it
was first
constructed in
1889, the Eiffel
Tower in Paris,
France, was the
tallest structure in
the world. In
1975, the CN
Tower in Toronto, Canada, became the world’s tallest
structure. The CN Tower is 153 ft less than twice the
height of the Eiffel Tower, and the sum of their
heights is 2799 ft. How tall is each tower?
85. Pacific islands land area: In the South Pacific, the
island nations of Tahiti and Tonga have a combined
land area of 692 mi
2
. Tahiti’s land area is 112 mi
2
more than Tonga’s. What is the land area of each
island group?
86. Card games: On a cold winter night, in the lobby
of a beautiful hotel in Sante Fe, New Mexico, Marc
and Klay just barely beat John and Steve in a close
game of Trumps. If the sum of the team scores was
990 points, and there was a 12-point margin of
victory, what was the final score?
Average Price Quantity Sold Production
(in U.S. dollars) (Demand) (Supply)
22.99 12 7
21.49 14 6
23.99 11 7
26.99 9 11
25.99 8 10
27.99 8 13
24.49 10 9
26.49 9 11
cob19545_ch06_575-591.qxd 10/5/10 1:15 PM Page 590

6–17 Section 6.2 Linear Systems in Three Variables with Applications 591
College Algebra G&M—
Given any two points, the equation of a line through these points can be found using a system of equations. While
there are certainly more efficient methods, using a system here will show how we can find equations for polynomials
of higher degree. The key is to note that each point will yield an equation of the form . For instance, the
points (3, 6) and yield the system
87. Use a system of equations to find the equation of the line containing the points (2, 7) and .
88. Use a system of equations to find the equation of the line containing the points and .13, 7219, 12
14, 52
e
6 ⴝ 3m ⴙ b
ⴚ4 ⴝⴚ2m ⴙ b
.1ⴚ2, ⴚ42
y ⴝ mx ⴙ b
䊳
EXTENDING THE CONCEPT
89. Federal income tax reform has been a hot political
topic for many years. Suppose tax plan A calls for
a flat tax of 20% tax on all income (no deductions
or loopholes). Tax plan B requires taxpayers to pay
$5000 plus 10% of all income. For what income
level do both plans require the same tax?
90. Suppose a certain amount of money was invested at
6% per year, and another amount at 8.5% per year,
with a total return of $1250. If the amounts
invested at each rate were switched, the yearly
income would have been $1375. To the nearest
whole dollar, how much was invested at each rate?
䊳
MAINTAINING YOUR SKILLS
91. (4.2) Use the rational zeroes theorem to write the
polynomial in completely factored form:
92. (2.2) Given the tool box function sketch
the graph of F1x2
冟
x 3
冟
2.
f 1x2
冟
x
冟
,
3x
4
19x
3
15x
2
27x 10.
93. (3.2) Graph and state the
interval where
94. (5.5) Solve for x (rounded to the nearest
thousandth): 33 77.5e
0.0052x
8.37.
f
1x2 0.
y x
2
6x 16
6.2 Linear Systems in Three Variables with Applications
The transition to systems of three equations in three variables requires a fair amount of
“visual gymnastics” along with good organizational skills. Although the techniques
used are identical and similar results are obtained, the third equation and variable give
us more to track, and we must work more carefully toward the solution.
A. Visualizing Solutions in Three Dimensions
The solution to an equation in one variable is the single number that satisfies the equa-
tion. For the solution is and its graph is a single point on the number
line, a one-dimensional graph. The solution to an equation in two variables, such as
is an ordered pair (x, y) that satisfies the equation. When we graph this
solution set, the result is a line on the xy-coordinate grid, a two-dimensional graph.
The solutions to an equation in three variables, such as are the ordered
triples (x, y, z) that satisfy the equation. When we graph this solution set, the result is a
plane in space, a graph in three dimensions. Recall a plane is a flat surface having infi-
nite length and width, but no depth. We can graph this plane using the intercept
method and the result is shown in Figure 6.15. For graphs in three dimensions, the xy-
plane is parallel to the ground (the y-axis points to the right) and z is the vertical axis.
To find an additional point on this plane, we use any three numbers whose sum is 6,
such as (2, 3, 1). Move 2 units along the x-axis, 3 units parallel to the y-axis, and 1 unit
parallel to the z-axis, as shown in Figure 6.16.
x y z 6,
x y 3,
x 2x 1 3,
LEARNING OBJECTIVES
In Section 6.2 you will see
how we can:
A. Visualize a solution in
three dimensions
B. Check ordered triple
solutions
C. Solve linear systems in
three variables
D. Recognize inconsistent
and dependent systems
E. Use a system of three
equations in three
variables to solve
applications
cob19545_ch06_575-591.qxd 11/26/10 2:17 PM Page 591
592 CHAPTER 6 Systems of Equations and Inequalities 6–18
College Algebra Graphs & Models—
WORTHY OF NOTE
We can visualize the location of a
point in space by considering a
large rectangular box 2 ft long
3 ft wide 1 ft tall, placed snugly
in the corner of a room. The floor is
the xy-plane, one wall is the
xz-plane, and the other wall is the
yz-plane. The z-axis is formed
where the two walls meet and the
corner of the room is the origin
(0, 0, 0). To find the corner of the
box located at (2, 3, 1), first locate
the point (2, 3) in the xy-plane (the
floor), then move up 1 ft.
y
x
z
(0, 0, 6)
(6, 0, 0)
(0, 6, 0)
Figure 6.15
y
x
z
(0, 0, 6)
(6, 0, 0)
(0, 6, 0)
2 units along x
(2, 3, 1)
3 units parallel y
1 unit parallel z
Figure 6.16
EXAMPLE 1
䊳
Finding Solutions to an Equation in Three Variables
Use a guess-and-check method to find four additional points on the plane
determined by
Solution
䊳
We can begin by letting then use any combination of y and z that sum to 6.
Two examples are (0, 2, 4) and (0, 5, 1). We could also select any two values for x
and y, then determine a value for z that results in a sum of 6. Two examples are
and
Now try Exercises 7 through 10
䊳
B. Solutions to a System of Three Equations in Three Variables
When solving a system of three equations in three variables, remember each equation
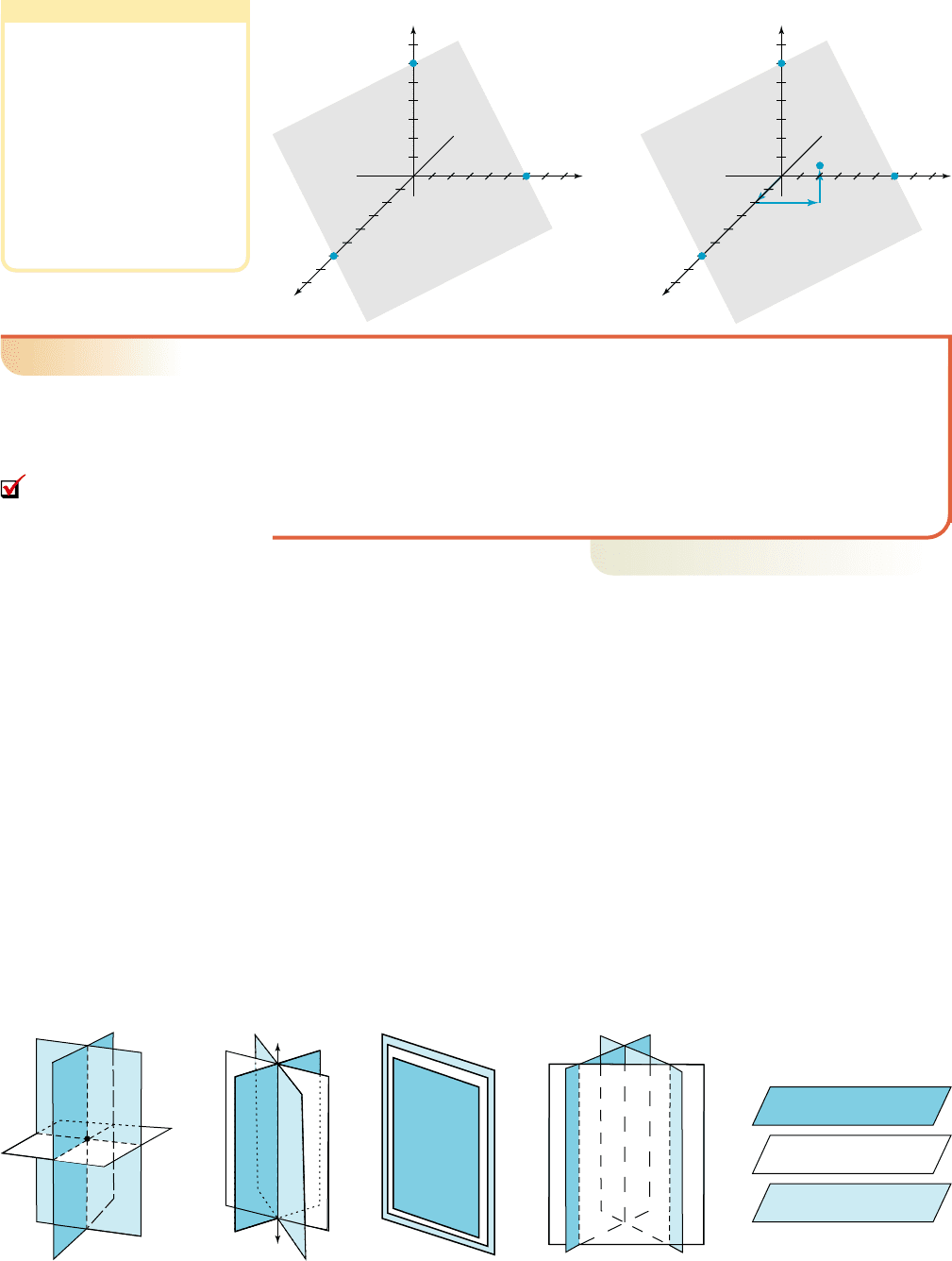
represents a plane in space. These planes can intersect in various ways, creating different
possibilities for a solution set (see Figures 6.17 to 6.20). The system could have a unique
solution (a, b, c), if the planes intersect at a single point (Figure 6.17) (the point satisfies
all three equations simultaneously). If the planes intersect in a line (Figure 6.18), the sys-
tem is linearly dependent and there is an infinite number of solutions. Unlike the two-
dimensional case, the equation of a line in three dimensions is somewhat complex, and the
coordinates of all points on this line are usually representedby a specialized ordered triple,
which we use to state the solution set. If the planes intersect at all points, the system has
coincident dependence (see Figure 6.18). This indicates the equations of the system
differ by only a constant multiple—they are all “disguised forms” of the same equation.
The solution set is any ordered triple (a, b, c) satisfying this equation. Finally, the system
may have no solutions. This can happen a number of different ways, most notably if
the planes either intersect or are parallel, as shown in Figure 6.20 (other possibilities
are discussed in the exercises). In the case of “no solutions,” an ordered triple may
satisfy none of the equations, only one of the equations, only two of the equations, but
not all three equations.
18, 3, 12.12, 9, 12
x 0,
x y z 6.
Figure 6.17 Figure 6.18 Figure 6.19 Figure 6.20
Unique solution Linear
dependence
Coincident
dependence
No solutions
A. You’ve just seen how
we can visualize a solution in
three dimensions
cob19545_ch06_592-604.qxd 10/5/10 1:16 PM Page 592

6–19 Section 6.2 Linear Systems in Three Variables with Applications 593
College Algebra Graphs & Models—
EXAMPLE 2
䊳
Determining If an Ordered Triple Is a Solution
Determine if the ordered triple is a solution to the systems shown.
a. b.
Solution
䊳
Substitute 1 for x, for y, and 3 for z in the first system.
a.
No, the ordered triple is not a solution to the first system. Now use
the same substitutions in the second system.
b.
The ordered triple is a solution to the second system only.
Now try Exercises 11 and 12
䊳
As with systems of two equations in two variables, solutions to larger systems can also
be checked by storing values using the keys, and entering each equation on the
home screen of a graphing calculator. The screens shown in Figures 6.21 and 6.22
illustrate this process for Example 2(b).
ALPHA
11, 2, 32
•
3x 2y z 4
2x 3y 2z 2
x y 2z 9
S •
3112 2122 1324
2112 3122 2132 2
112 122 2132 9
S •
4 4 true
2 2 true
9 9 true
11, 2, 32
•
x 4y z10
2x 5y 8z 4
x 2y 3z4
S •
112 4122 13210
2112 5122 8132 4
112 2122 31324
S •
10 10 true
16 4 false
4 4 true
2
•
3x 2y z 4
2x 3y 2z 2
x y 2z 9
•
x 4y z 10
2x 5y 8z 4
x 2y 3z 4
11, 2, 32
B. You’ve just seen how
we can check ordered triple
solutions
C. Solving Systems of Three Equations in Three Variables
Using Elimination
From Section 6.1, we know that two systems of equations are equivalent if they have
the same solution set. The systems
are equivalent, as both have the unique solution In addition, it is evident that
the second system can be solved more easily, since R2 and R3 have fewer variables
than the first system. In the simpler system, mentally substituting 1 for z into R2 im-
mediately gives and these values can be back-substituted into the first equation
to find that This observation guides us to a general approach for solving larger
systems—we would like to eliminate variables in the second and third equations, un-
til we obtain an equivalent system that can easily be solved by back-substitution. To
begin, let’s review the three operations that “transform” a given system, and produce
an equivalent system.
x 3.
y 1,
13, 1, 12.
and
•
2x y 2z 7
y 4z 5
z 1
•
2x y 2z 7
x y z 1
2y z 3
Figure 6.21 Figure 6.22
cob19545_ch06_592-604.qxd 10/5/10 1:16 PM Page 593

594 CHAPTER 6 Systems of Equations and Inequalities 6–20
College Algebra Graphs & Models—
Operations That Produce an Equivalent System
1. Changing the order of the equations.
2. Replacing an equation by a nonzero constant multiple of that equation.
3. Replacing an equation with the sum of two equations from the system.
Building on the ideas from Section 6.1, we develop the following approach for
solving a system of three equations in three variables.
Solving a System of Three Equations in Three Variables
1. Write each equation in standard form:
2. If the “x” term in any equation has a coefficient of 1, interchange equations
(if necessary) so this equation becomes R1.
3. Use the x-term in R1 to eliminate the x-terms from R2 and R3. The original
R1, with the new R2 and R3, form an equivalent system that contains a
smaller “subsystem” of two equations in two variables.
4. Solve the subsystem for either x or y and keep the result as the new R3. The
result is an equivalent system that can be solved using back-substitution.
We’ll begin by solving the system using the elimination
method and the procedure outlined. In Example 3, the notation
indicates the equation in row 1 has been multiplied by and added to the equation in
row 2, with the result placed in the system as the new row 2.
2
2R1 R2 S R2
•
2x y 2z 7
x y z 1
2y z 3
Ax By Cz D.
EXAMPLE 3
䊳
Solving a System of Three Equations in Three Variables
Solve using elimination: .
Solution
䊳
1. The system is in standard form.
2. If the x-term in any equation has a coefficient of 1, interchange equations so
this equation becomes R1.
3. Use R1 to eliminate the x-term in R2 and R3. Since R3 has no x-term, the only
elimination needed is the x-term from R2. Using will eliminate
this term:
The new R2 is The original R1 and R3, along with the new R2
form an equivalent system that contains a smaller subsystem
•
x y z 1
y 4z 5
2y z 3
S
2R1 R2 S R2
R3 S R3
•
x y z 1
2x y 2z 7
2y z 3
y 4z 5.
2R1
2x 2y 2z 2
R2
2x y 2z 7
0x 1y 4z 5
y 4z 5
2R1 R2
•
x y z 1
2x y 2z 7
2y z 3
S
R2 4 R1
•
2x y 2z 7
x y z 1
2y z 3
•
2x y 2z 7
x y z 1
2y z 3
sum
simplify
new
equivalent
system
cob19545_ch06_592-604.qxd 10/5/10 1:16 PM Page 594

6–21 Section 6.2 Linear Systems in Three Variables with Applications 595
College Algebra Graphs & Models—
4. Solve the subsystem for either y or z, and keep the result as a new R3. We
choose to eliminate y using
The new R3 is
The new R3, along with the original R1 and R2 from step 3, form an
equivalent system that can be solved using back-substitution. Substituting
1 for z in R2 yields y 1. Substituting 1 for z and 1 for y in R1 yields
The solution is Check this result using the keys, as illustrated
following Example 2.
Now try Exercises 13 through 16
䊳
While not absolutely needed for the elimination process, there are two reasons for
wanting the coefficient of x to be “1” in R1. First, it makes the elimination method
more efficient since we can more easily see what to use as a multiplier. Second, it lays
the foundation for developing other methods of solving larger systems. If no equation
has an x-coefficient of 1, we simply use the y- or z-variable instead (see Example 7).
Since solutions to larger systems generally are worked out in stages, we will some-
times track the transformations used by writing them between the original system and
the equivalent system, rather than to the left as we did in Section 6.1.
Here is an additional example illustrating the elimination process, but in abbrevi-
ated form. Verify the calculations indicated using a separate sheet.
EXAMPLE 4
䊳
Solving a System of Three Equations in Three Variables
Solve using elimination:
Solution
䊳
1. Write the equations in standard form:
2.
3. Using will eliminate the x-term from R2, yielding
Using eliminates the x-term from R3, yielding
4. Using will eliminate z from the subsystem, leaving
•
x 3y z 5
5y 2z 18
11y z 18
2R3 R2 S R3
•
x 3y z 5
5y 2z 18
27y 54
27y 54.2R3 R2
•
x 3y z 5
x 2y 3z 13
2x 5y z 8
R1 R2 S R2
2R1 R3 S R3
•
x 3y z 5
5y 2z 18
11y z 18
11y z 18.2R1 R3
5y 2z 18.R1 R2
•
2x 5y z 8
x 2y 3z 13
x 3y z 5
R3 4 R1
•
x 3y z 5
x 2y 3z 13
2x 5y z 8
•
2x 5y z 8
x 2y 3z 13
x 3y z 5
•
5y 2x z 8
x 3z 2y 13
z 3y x 5
.
ALPHA
13, 1, 12.
x 3.
•
x y z 1
y 4z 5
z 1
S
2R2 R3 S R3
•
x y z 1
y 4z 5
2y z 3
z 1.
2R2
2y 8z 10
R3
2y z 3
0y 7z 7
z 1
2R2 R3:
S
S
S
equivalent
system
equivalent
system
equivalent
system
sum
simplify
new
equivalent
system
cob19545_ch06_592-604.qxd 10/5/10 1:16 PM Page 595

596 CHAPTER 6 Systems of Equations and Inequalities 6–22
College Algebra Graphs & Models—
Solving for y in R3 yields: , showing y 2. Substituting 2 for y in R2 gives,
substitute 2 for
y
simplify
subtract 10
divide by 2
Substituting 2 for y and 4 for z in R1 gives,
substitute 2 for
y
, 4 for
z
simplify
subtract 2
The solution is (3, 2, 4).
Now try Exercises 17 through 20
䊳
D. Inconsistent and Dependent Systems
As mentioned, it is possible for larger systems to have no solutions or an infinite num-
ber of solutions. As with our work in Section 6.1, an inconsistent system (no solutions)
will produce inconsistent results, ending with a statement such as or some
other contradiction.
EXAMPLE 5
䊳
Attempting to Solve an Inconsistent System
Solve using elimination:
Solution
䊳
1. This system has no equation where the coefficient of x is 1.
2. We can still use R1 to begin the solution process, but this time we’ll use the
variable y since it does have coefficient 1.
Using eliminates the y-term from R2, leaving But
using to eliminate the y-term from R3 results in a contradiction:2R1 R3
7x 2z 4.2R1 R2
•
2x y 3z 3
3x 2y 4z 2
4x 2y 6z 7
.
0 3
x 3
x 2 5
x 3122 4 5
z 4
2 z 8
10 2z 18
5 122 2z 18
27
y
27
54
27
C. You’ve just seen how
we can solve linear systems in
three variables
We conclude the system is inconsistent. The answer is the empty set and
we need work no further.
Now try Exercises 21 and 22
䊳
Unlike our work with systems having only two variables, systems in three variables
can have two forms of dependence—linear dependence (Figure 6.18) or coincident
dependence (Figure 6.19). To help understand linear dependence, consider a system of
two equations in three variables: Each of these equations
represents a plane, and unless the planes are parallel, their intersection will be a line. As
in Section 6.1, we can state solutions to a dependent system using set notation with two
of the variables written in terms of the third, or as an ordered triple using a parameter.
The relationships named can then be used to generate specific solutions to the system.
e
2x 3y z 5
x 3y 2z 1
.
,
4x 2y 6z 6
4x 2y 6z 7
0x 0y 0z 1
0 1
2R1
R3
2R1
R2
4x 2y 6z 6
3x 2y 4z 2
7x 2z 4
contradiction
cob19545_ch06_592-604.qxd 10/5/10 1:16 PM Page 596

6–23 Section 6.2 Linear Systems in Three Variables with Applications 597
College Algebra Graphs & Models—
Systems with two equations and two variables or three equations and three vari-
ables are called square systems, meaning there are exactly as many equations as there
are variables. A system of linear equations cannot have a unique solution unless there
are at least as many equations as there are variables in the system.
EXAMPLE 6
䊳
Solving a Dependent System
Solve using elimination:
Solution
䊳
We immediately note that eliminates the y-term from R2, yielding
and the new system . This means (x, y, z) will
satisfy both equations only when (the x-coordinate must be 4 less than
the z-coordinate). Since x is written in terms of z, we substitute for x in
either equation to find how y is related to z. Using R2 in the original system we
have: , which yields (verify). This means the
y-coordinate of the solution must be more than . In set notation, the solution is
. Randomly choosing 2, and 7,
the solutions would be , respectively. Verify
that these satisfy both equations. Using p as a parameter, the solution could be
written in parameterized form.
Now try Exercises 23 through 26
䊳
The system in Example 6 was nonsquare, and we knew ahead of time the system
would be dependent. The system in Example 7 is square, but only by applying the
elimination process can we determine the nature of its solution(s).
EXAMPLE 7
䊳
Solving a Dependent System
Solve using elimination:
Solution
䊳
This system has no equation where the coefficient of x is 1. We will still use R1,
noting that eliminates the z-term from R2, yielding (there is
no z-term in R3).
We next solve the subsystem. Using eliminates the y-term in R3, but
also all other terms:
Since R3 is the same as 2R2, the system is linearly dependent and equivalent to
We can solve for y in R2 to write y in terms of x:
Substituting for y in R1 enables us to also write z in terms of x:5x ⫺ 4
y ⫽ 5x ⫺ 4.e
3x ⫺ 2y ⫹ z ⫽⫺1
5x ⫺ y ⫽ 4
.
⫺10x ⫹ 2y ⫽⫺8
10x ⫺ 2y ⫽
8
0x ⫹ 0y ⫽ 0
0 ⫽ 0
⫺2R2
⫹
R3
⫺2R2 ⫹ R3
•
3x ⫺ 2y ⫹ z ⫽⫺1
2x ⫹ y ⫺ z ⫽ 5
10x ⫺ 2y ⫽ 8
R1 ⫹ R2 S R2
R3 S R3
•
3x ⫺ 2y ⫹ z ⫽⫺1
5x ⫺ y ⫽ 4
10x ⫺ 2y ⫽ 8
5x ⫺ y ⫽ 4R1 ⫹ R2
•
3x ⫺ 2y ⫹ z ⫽⫺1
2x ⫹ y ⫺ z ⫽ 5
10x ⫺ 2y ⫽ 8
.
1
p ⫺ 4,
1
5
p ⫹
3
5
, p2
1⫺7, 0, ⫺32, 1⫺2, 1, 22, and 13, 2, 72
z ⫽⫺3,51x, y, z,2 | x ⫽ z ⫺ 4, y ⫽
1
5
z ⫹
3
5
, z 僆 ⺢6
1
5
z
3
5
y ⫽
1
5
z ⫹
3
5
⫺1z ⫺ 42⫺ 5y ⫹ 2z ⫽ 1
z ⫺ 4
x ⫽ z ⫺ 4
e
2x ⫹ 5y ⫺ 3z ⫽⫺5
x ⫺z ⫽⫺4
x ⫺ z ⫽⫺4
R1 ⫹ R2
e
2x ⫹ 5y ⫺ 3z ⫽⫺5
⫺x ⫺ 5y ⫹ 2z ⫽ 1
.
S
sum
result
cob19545_ch06_592-604.qxd 12/1/10 3:07 PM Page 597

598 CHAPTER 6 Systems of Equations and Inequalities 6–24
College Algebra Graphs & Models—
R1
substitute for
y
distribute
simplify
solve for
z
The solution set is Three of the
infinite number of solutions are for for
Verify these triples satisfy all three equations. Again
using the parameter p, the solution could be written as .
Now try Exercises 27 through 30
䊳
For coincident dependence the equations in a system differ by only a constant
multiple. After applying the elimination process—all variables are eliminated from the
other equations, leaving statements that are always true (such as or some other).
For additional practice solving various kinds of systems, see Exercises 31 to 44.
E. Applications
Applications of larger systems are simply an extension of our work with systems of
two equations in two variables. Once again, the applications come in a variety of forms
and from many fields. In the world of business and finance, systems can be used to
diversify investments or spread out liabilities, a financial strategy hinted at in Example 8.
EXAMPLE 8
䊳
Modeling the Finances of a Business
A small business borrowed $225,000 from three different lenders to expand their
product line. The interest rates were 5%, 6%, and 7%. Find how much was
borrowed at each rate if the annual interest came to $13,000 and twice as much
was borrowed at the 5% rate than was borrowed at the 7% rate.
Solution
䊳
Let x, y, and z represent the amounts borrowed at 5%, 6%, and 7%, respectively.
This means our first equation is (in thousands). The second
equation is determined by the total interest paid, which was $13,000:
The third is found by carefully reading the problem.
“twice as much was borrowed at the 5% rate than was borrowed at the 7% rate,”
or
These equations form the system: The x-term of
the first equation has a coefficient of 1. Written in standard form we have:
multiply R2 by 100
Using will eliminate the x term in R2, while will
eliminate the x-term in R3.
R1 x y z 225
R3 x 2z 0
y 3z 225
5R1 5x 5y 5z 1125
R2 5x 6y 7z 1300
y 2z 175
R1 R35R1 R2
•
x y z 225
5x 6y 7z 1300
x 2z 0
R1
R2
R3
•
x y z 225
0.05x 0.06y 0.07z 13
x 2z
.
x 2z.
0.05x 0.06y 0.07z 13.
x y z 225
2 2
1
p, 5p 4, 7p 92
11, 9, 162 for x 1.
x 2, andx 0, 12, 6, 5210, 4, 92
51x, y, z2
|
x 僆 ⺢, y 5x 4, z 7x 96.
z 7x 9
7x z 9
3 x 10x 8 z 1
5x 4 3 x 215x 42 z 1
3 x 2y z 1
D. You’ve just seen how
we can recognize inconsistent
and dependent systems
cob19545_ch06_592-604.qxd 10/5/10 1:16 PM Page 598

6–25 Section 6.2 Linear Systems in Three Variables with Applications 599
College Algebra Graphs & Models—
The new R2 is and the new R3 (after multiplying by ) is
yielding the equivalent system
Solving the subsystem using yields Back-substitution
shows and yielding the solution (100, 75, 50). This means $50,000
was borrowed at the 7% rate, $75,000 was borrowed at 6%, and $100,000 at 5%.
A “substitution check” on a graphing calculator verifies this solution is correct
(see Figures 6.23 and 6.24).
x 100,y 75
z 50.R2 R32 2
•
x y z 225
y 2z 175
y 3z 225
.y 3z 225,
1y 2z 175,
Figure 6.23
Figure 6.24
E. You’ve just seen how
we can use a system of three
equations in three variables to
solve applications
Now try Exercises 47 through 56
䊳
4. If a system is linearly dependent, the
ordered triple solutions can be written in terms of a
single variable called a(n) .
3 3
䊳
CONCEPTS AND VOCABULARY
Fill in the blank with the appropriate word or phrase. Carefully reread the section if needed.
1. The solution to an equation in three variables is an
ordered .
2. The graph of the solutions to an equation in three
variables is a(n) .
5. Find a value of z that makes the ordered triple
a solution to
Discuss/Explain how this is accomplished.
2x y z 4.12, 5, z2
3. Systems that have the same solution set are called
.
6. Explain the difference between linear dependence
and coincident dependence, and describe how the
equations are related.
6.2 EXERCISES
Use the keys on a graphing calculator to determine
if the given ordered triples are solutions to the system. If
not a solution, identify which equation(s) are not satisfied.
11.
12. •
2x 3y z 9
5x 2y z 32;
14, 5, 22
x y 2z 13
15, 4, 112
•
x y 2z 1
4x y 3z 3
;
10, 3, 22
3x 2y z 4
13, 4, 12
ALPHA
䊳
DEVELOPING YOUR SKILLS
Find any four ordered triples that satisfy the equation
given.
7.
8.
9.
10. 2x y 3z 12
x y 2z 6
3x y z 8
x 2y z 9
cob19545_ch06_592-604.qxd 10/5/10 1:16 PM Page 599
