Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models

Подождите немного. Документ загружается.

EXERCISES

Solve each application.

47. Jeffery borrows $600.00 from his dad, who decides it’s best to charge him interest. Three months later Jeff repays

the loan plus interest, a total of $627.75. What was the annual interest rate on the loan?

48. To save money for her ﬁrst car, Cheryl invests the $7500 she inherited in an account paying 7.8% interest compounded

monthly. She hopes to buy the car in 6 yr and needs $12,000. Is this possible?

49. To save up for the vacation of a lifetime, Al-Harwi decides to save $15,000 over the next 4 yr. For this purpose he

invests $260 every month in an account paying interest compounded monthly. (a) Is this monthly amount

sufﬁcient to meet the four-year goal? (b) If not, ﬁnd the minimum amount he needs to deposit each month that will

enable him to meet this goal in 4 yr.

50. Eighty prairie dogs are released in a wilderness area in an effort to repopulate the species. Five years later a

statistical survey reveals the population has reached 1250 dogs. Assuming the growth was exponential,

approximate the growth rate to the nearest tenth of a percent.

SECTION 5.7 Exponential, Logarithmic, and Logistic Equation Models

KEY CONCEPTS

•

The choice of regression models generally depends on: (a) whether the graph appears to ﬁt the data, (b) the

context or situation that generated the data, and (c) certain tests applied to the data.

•

The regression equation can be used to extrapolate or predict future values or occurrences. When using

extrapolation, values are projected beyond the given set of data.

•

The regression equation can be used to interpolate or approximate intermediate values. When using interpolation,

the values occur between those given in the data set.

EXERCISES

51. Vehicle fuel economy: While the average fuel economy of light trucks rose

signiﬁcantly in the late 1970s and early 1980s, this growth seemed to slow

signiﬁcantly thereafter, and increased at a much slower rate through the 1990s

and beyond. The fuel economy for selected years is shown in the table

. Draw a scatterplot of the data then complete the following.

Source:

Data from the Pew Charitable Trusts.

a. Decide on an appropriate form of regression and ﬁnd a regression equation.

b. Use the regression equation to estimate the average fuel economy for light

trucks in the year 1988.

c. If current trends continue, in what year will average fuel economy

surpass 18.5 mi/gal?

52. Biological studies—cell division: The relationship between cell size and cell

division (mitosis) is a common object of biological research. In many cells, a

natural mechanism exists that triggers cell division only after the cell has reached

a certain size. If the supply of nutrients is scarce, cell growth slows after an initial

spurt, and the time between cell divisions is lengthened. Suppose the normal size

of a certain cell is 4 microns (four millionths of a meter), and the data in the table

track the growth of this cell over time. Draw a scatterplot for the data and complete

the following.

a. Decide on an appropriate form of regression and ﬁnd a regression equation.

b. Use the regression equation to estimate the size of the cell after 2.5 hr.

c. If mitosis (cell division) begins when the cell has grown to 196% of its

original size, how long until mitosis occurs?

11975 S 02

570 CHAPTER 5 Exponential and Logarithmic Functions 5–92

College Algebra G&M—

Year Average

Miles per Gal

1 12.5

5 15.5

10 16.8

15 17.5

20 17.6

25 17.6

30 17.8

11975 S 02

Time t Cell Growth G

(hr) (microns)

1 5.3

2 6.4

3 7.1

4 7.5

5 7.8

6 7.9

cob19545_ch05_567-574.qxd 9/2/10 9:53 PM Page 570

5–93 Practice Test 571

College Algebra G&M—

1. Write the expression in exponential

form.

2. Write the expression in logarithmic form.

3. Write the expression as a sum or

difference of logarithmic terms.

4. Write the expression as a

single logarithm.

Solve for x using the uniqueness property.

5. 6.

Given and evaluate the

following without the use of a calculator:

7. 8.

Graph using transformations of the parent function.

Verify answers using a graphing calculator.

10.

11. Use the change-of-base formula to evaluate. Verify

results using a calculator.

a. b.

12. State the domain and range of

and determine if f is a one-to-one function. If so,

ﬁnd its inverse. If not, restrict the domain of f to

create a one-to-one function, then ﬁnd the inverse of

this new function, including the domain and range.

Solve each equation.

13.

14.

15. A copier is purchased new for $8000. The machine

loses 18% of its value each year and must be

replaced when its value drops below $3000. How

many years will the machine be in service?

16. In 1957, scientist

Stanley Stevens

proposed a

mathematical

model that

attempted to

compare the actual

strength of a

physical stimulus

log

x ⫹ log

1x ⫹ 42⫽ 1

x⫺1

⫽ 89

1x2⫽ 1x ⫺ 22

⫺ 3

log

0.235log

100

h1x2⫽ log

1x ⫺ 22⫹ 1

g1x2⫽⫺2

x⫺1

⫹ 3

log

0.6log

log

5 ⬇ 1.72,log

3 ⬇ 0.48

⫽

x⫺7

⫽ 125

log

m ⫹ 1

2log

n ⫺

log

1/2

⫽ 5

log

81 ⫽ 4

with the human perception (dead-reckoning) of its

strength. The model has been widely applied in

comparisons of weight, sound, pressure, and other

areas. If M represents the measured strength of the

stimulus, and P the human perception of its

strength, Stevens’law can be written as

, where and k are

constants determined by the type of stimulation

applied. In a controlled experiment, subjects were

given a known amount of weight to lift, then asked to

select an unmarked weight they felt was equal to half

the known weight. (a) Solve the equation for P and

(b) use the result to determine what was perceived to

be half of a 40-lb weight (assume and

17. The number of ounces of unreﬁned platinum

drawn from a mine is modeled by

where Q(t) represents

the number of ounces mined in t months. How many

months did it take for the number of ounces mined

to exceed 3000?

18. Jacob decides to save $4000 over the next 5 yr so

that he can present his wife with a new diamond ring

for their 20th anniversary. He invests $50 every

month in an account paying interest

compounded monthly. (a) Is this amount sufﬁcient to

meet the 5-yr goal? (b) If not, ﬁnd the minimum

amount he needs to save monthly that will enable

him to meet this goal.

19. Chaucer is a typical Welsh Corgi puppy. During his

ﬁrst year of life, his weight very closely follows the

model , where W(t) is his

weight in pounds after t weeks and

a. How much will Chaucer weigh when he is 26

weeks old (to the nearest one-tenth pound)?

b. To the nearest week, how old is Chaucer when he

weighs 12 lb?

20. Using time-lapse photography,

the growth of a stain is tracked in

0.2 second intervals, as a small

amount of liquid is dropped on

various fabrics. Use the data

given to draw a scatterplot and

decide on an appropriate

regression model. How

long, to the nearest hundredth of

a second, did it take the stain to

reach a size of 15 mm?

8 ⱕ t ⱕ 52.

W1t2⫽ 6.79 ln t ⫺ 11.97

Q1t2⫽⫺2600 ⫹ 1900 ln 1t2,

␣ ⫽ 0.95

k ⫽ 0.89

␣log P ⫽ log k ⫹ ␣ log M

PRACTICE TEST

Time Size

(sec) (mm)

0.2 0.39

0.4 1.27

0.6 3.90

0.8 10.60

1.0 21.50

1.2 31.30

1.4 36.30

1.6 38.10

1.8 39.00

Exercise 20

cob19545_ch05_567-574.qxd 9/3/10 8:37 PM Page 571

572 CHAPTER 5 Exponential and Logarithmic Functions 5–94

College Algebra G&M—

CALCULATOR EXPLORATION AND DISCOVERY

Investigating Logistic Equations

As we saw in Section 5.5, logistic models have the form where a, b, and c are constants and P(t)

represents the population at time t. For populations modeled by a logistic curve (sometimes called an “S” curve), growth

is very rapid at ﬁrst (like an exponential function), but this growth begins to slow down and level off due to various factors.

This Calculator Exploration and Discovery is designed to investigate the effects that a and c have on the resulting graph.

I. Investigating a: From our earlier observation, as t becomes larger and larger,

the term becomes smaller and smaller (approaching 0) because it is a

decreasing function: as If we allow that the term

eventually becomes so small it can be disregarded, what remains is

or c. This is why c is called the capacity constant and the population can get no

larger than c. In Figure 5.65, the graph of

and is shown using a lighter line, while the graph of

and is given in bold.

Also note that if a is held constant, smaller values of c cause the “interior” of the S curve to grow at a slower rate than

larger values, a concept studied in some detail in a Calculus I class.

II. Investigating c: If and we note the ratio represents the initial population.

This also means for constant values of c, larger values of a make the ratio smaller; while smaller values

of a make the ratio larger. From this we conclude that a primarily affects the initial population. In

Figures 5.66 and 5.67 shown next, (from I) is graphed using a lighter line, while the graph of

and are shown in bold.P1t2⫽

1000

1 ⫹ 500e

⫺1x

1a ⫽ 50021a ⫽ 52P1t2⫽

1000

1 ⫹ 5e

⫺1x

P1t2⫽

1000

1 ⫹ 50e

⫺1x

1 ⫹ a

P102⫽

1 ⫹ a

t ⫽ 0, ae

⫺bt

⫽ ae

⫽ a,

c ⫽ 7502,P1t2⫽

750

1 ⫹ 50e

⫺1x

1a ⫽ 50, b ⫽ 1,

c ⫽ 10002

P1t2⫽

1000

1 ⫹ 50e

⫺1x

1a ⫽ 50, b ⫽ 1,

P1t2⫽

⫺bt

S 0.t Sq,

⫺bt

P1t2⫽

1 ⫹ ae

⫺bt

⫺150

1100

10⫺1

Figure 5.65

⫺150

1100

10⫺1

Figure 5.66

⫺150

1100

⫺110

Figure 5.67

Note that changes in a appear to have no effect on the rate of growth in the interior of the S curve.

The following exercises are based on the population of an ant colony, modeled by the logistic function

. Respond to Exercises 1 through 6 without the use of a calculator.

Exercise 1: Identify the values of a, b, and c for this logistics curve.

Exercise 2: What was the approximate initial population of the colony?

Exercise 3: Which gives a larger initial population:(a) and or (b) and

Exercise 4: What is the maximum population capacity for this colony?

Exercise 5: Which causes a slower population growth: (a) and or (b) and

Exercise 6: Verify your responses to Exercises 2 through 6 using a graphing calculator.

a ⫽ 25?c ⫽ 3000a ⫽ 25c ⫽ 2000

a ⫽ 15?c ⫽ 3000a ⫽ 25c ⫽ 2500

P1t2⫽

2500

1 ⫹ 25e

⫺0.5x

cob19545_ch05_567-574.qxd 11/30/10 6:11 PM Page 572

5–95 Strengthening Core Skills 573

College Algebra G&M—

The HerdBurn Scale—What’s Hot and What’s Not

The human mouth can easily distinguish between heat levels (the

burning sensation) when eating foods “spiced” with various peppers.

The level of “heat” is generally given in Scoville units, which is a

measure of the element capsaicin that causes the burn. Sweet bell

peppers and others have no capsaicin and a Scoville rating of 0, while

red habanero peppers have a Scoville rating of near 500,000. Although

inedible, laboratory grades of capsaicin can have a Scoville rating of

near 16,000,000! This range of values makes a unit scale impractical for

common use, and a logarithmic scale once again becomes more

desirable. Using the newly developed HerdBurn scale (hb), we have the

following measures of “heat” for well known peppers of various types.

STRENGTHENING CORE SKILLS

HerdBurn Units (hb) Chili Pepper General Sensation Caustic Power

0 sweet banana peppers not sensed none

1 cherry peppers delicate warmth none

2 pepperoncini peppers strong warmth none

2.5 Sonora peppers slight burn some reaction

3 ancho peppers moderate burn fanning the mouth

3.5 jalapeno peppers strong burn eyes water

4 hidalgo peppers sizzling burn pain threshold

4.5 cayenne peppers scorching burn painful

5 Bahamian peppers blistering burn very painful

5.5 habanero peppers ruthless burn intense pain

6 naga jolokia peppers merciless burn debilitating

6.5 military grade pepper spray inedible incapacitating

7 laboratory grade capsaicin inedible ruinous

7.2 pure capsaicin inedible deadly

The HerdBurn Scale

Similar to working with decibel levels or the Richter scale, we compare how many times hotter one pepper is than

another by recognizing the values given are powers of 10. For example, a red habanero (5.7 hb), is about two times as

hot as an orange habanero (5.4 hb): , but nearly 100 times hotter than a red jalapeno pepper

(3.7 hb): . Use this information to complete the following exercises.

Exercise 1: The “heat” in a rocotillo pepper measures about 3.4 on the HerdBurn scale, while a Jamaican hot pepper

measures near 5.5. How many times hotter is the Jamaican pepper?

Exercise 2: A naga jolokia (6.0 hb) pepper is about 63 times as hot as a serrano pepper. What is the HerdBurn number

for a serrano pepper?

5.7

3.7

⫽ 10

5.7

5.4

⫽ 10

0.3

⬇ 2

cob19545_ch05_567-574.qxd 11/30/10 5:33 PM Page 573

574 CHAPTER 5 Exponential and Logarithmic Functions 5–96

College Algebra G&M—

Use the quadratic formula to solve for x.

3. Use substitution to show that is a zero of

4. Graph using transformations of a basic function:

5. Find and and comment on what

you notice: .

6. State the domain of h(x) in interval notation:

7. According to the 2002 National Vital Statistics

Report (Vol. 50, No. 5, page 19) there were 3100

sets of triplets born in the United States in 1991, and

6740 sets of triplets born in 1999. Assuming the

relationship (year, sets of triplets) is linear: (a) ﬁnd

an equation of the line, (b) explain the meaning of

the slope in this context, and (c) use the equation to

estimate the number of sets born in 1996, and to

project the number of sets that will be born in 2007

if this trend continues.

8. State the following geometric formulas:

a. area of a circle c. perimeter of a rectangle

b. Pythagorean theorem d. area of a trapezoid

9. Graph the following piecewise-deﬁned function and

state its domain, range, and intervals where it is

increasing and decreasing.

10. Solve the inequality and write the solution in

interval notation: .

11. Use the rational roots theorem to ﬁnd all zeroes of

12. Given ﬁnd k, where

Then ﬁnd the inverse function using the algebraic

method, and verify that .

13. Solve the formula (the

volume of a paraboloid) for the

variable b.

V ⫽

␲b

⫺1

1k2⫽ 25

k ⫽ f1252.f 1c2⫽

c ⫹ 32,

1x2⫽ x

⫺ 3x

⫺ 12x

⫹ 52x ⫺ 48

2x ⫹ 1

x ⫺ 3

ⱖ 0

h1x2⫽ •

⫺4 ⫺10 ⱕ x 6 ⫺2

⫺x

⫺2 ⱕ x 6 3

3x ⫺ 18 x ⱖ 3

h1x2⫽

1x ⫹ 3

⫹ 6x ⫹ 8

1x2⫽ x

⫺ 2; g1x2⫽ 1

x ⫹ 2

1g ⴰ f 21x21f ⴰ g21x2

y ⫽ 21x ⫹ 2

⫺ 3.

1x2⫽ x

⫺ 8x ⫹ 41

4 ⫹ 5i

⫹ 19x ⫽ 36

⫺ 4x ⫹ 53 ⫽ 0

14. Use the Guidelines for Graphing to graph

a. b.

15. For , (a) ﬁnd , (b) graph both

functions and verify they are symmetric to the line

, and (c) show they are inverses using

composition.

16. Solve for x:

17. Solve for x:

18. Once in orbit, satellites are often powered by

radioactive isotopes. From the natural process of

radioactive decay, the power output declines over a

period of time. For an initial amount of 50 g,

suppose the power output is modeled by the function

where p(t) is the power output in

watts, t days after the satellite has been put into

service. (a) Approximately how much power

remains 6 months later (assume 1 mo.

days)? (b) How many years until only one-fourth of

the original power remains?

19. Simon and Christine own a sport wagon and a

minivan. The sport wagon has a power curve

that is closely modeled by

where H(r) is the horsepower at r rpm, with

. The power curve for the minivan

is , for .

a. How much horsepower is generated by each

engine at 3000 rpm?

b. At what rpm are the engines generating the same

horsepower?

c. If Christine wants the maximum horsepower

available, which vehicle should she drive? What

is the maximum horsepower?

20. Wilson’s disease is a hereditary disease that causes

the body to retain copper. Radioactive copper,

Cu,

has been used extensively to study and understand

this disease.

Cu has a relatively short half-life of

12.7 hr. How many hours will it take for a 5-g mass

Cu to decay to 1 g?

Solve using a graphing calculator.

21.

22.

23.

24.

25. 2

⫺x⫺6

⫽ x

⫹ x ⫺ 6

⫺ 25

⫺ 9

⫽ ln1x ⫹ 92⫹ 33

⫽ 1x ⫹ 5

5.2 ⫺ e

0.25 x

⫽ 4 ⫺ ln1x ⫹ 62

⫺ 9.2 ⫽ 5 ⫺ ln x

2600 6 r ⱕ 5800h1r2⫽ 193 ln r ⫺ 1464

2200 ⱕ r ⱕ 5600

H1r2⫽ 123 ln r ⫺ 897,

⬇ 30.5

p1t2⫽ 50e

⫺0.002t

ln1x ⫹ 32⫹ ln1x ⫺ 22⫽ ln1242.

10 ⫽⫺2e

⫺0.05x

⫹ 25.

y ⫽ x

⫺1

f 1x2⫽

2x ⫹ 3

r1x2⫽

⫹ 4

.p1x2⫽ x

⫺ 4x

⫹ x ⫹ 6.

CUMULATIVE REVIEW CHAPTERS R–5

cob19545_ch05_567-574.qxd 11/27/10 12:22 AM Page 574

College Algebra G&M—

Systems of

Equations and

Inequalities

CHAPTER OUTLINE

6.1 Linear Systems in Two Variables

with Applications 576

6.2 Linear Systems in Three Variables

with Applications 591

6.3 Nonlinear Systems of Equations

and Inequalities 604

6.4 Systems of Inequalities and

Linear Programming 615

CHAPTER CONNECTIONS

At the turn of the century, there was an

explosion in the number of handheld electronic

devices available to consumers. One device in

particular, the popular MP3 player, experienced

a phenomenal growth in demand. With high

demand and a large market, competition

between manufacturers and suppliers is often

ﬁerce, with each ﬁghting to earn and hold a

share of the market. One signiﬁcant factor in

who gains the largest share is the price charged

for the player, with suppliers willing to supply

more at a greater price, and consumers willing to

buy more at a lesser price. Determining where

the price will stabilize is an important component

in the economics of

“supply and demand.

” This

application occurs as Exercise 74 in Section 6.1.

Check out these other real-world connections:

䊳

Appropriate Measurements in Dietetics

(Section 6.1, Exercise 64)

䊳

Allocating Winnings to Different Investments

(Section 6.2, Exercise 53)

䊳

Market Pricing for Organic Produce

(Section 6.3, Exercise 66)

䊳

Minimizing Shipping Costs

(Section 6.4, Exercise 69)

575

cob19545_ch06_575-591.qxd 10/5/10 1:14 PM Page 575

6.1 Linear Systems in Two Variables with Applications

576 6–2

College Algebra G&M—

In earlier chapters, we used linear equations in two variables to model a number of

real-world situations. Graphing these equations gave us a visual image of how the

variables were related, and helped us better understand this relationship. In many

applications, two different measures of the independent variable must be considered

simultaneously, leading to a system of two linear equations in two unknowns. Here,

a graphical presentation once again supports a better understanding, as we explore sys-

tems and their many applications.

A. Solutions to a System of Equations

A system of equations is a set of two or more equations for which a common solution

is sought. Systems are widely used to model and solve applications when the informa-

tion given enables the relationship between variables to be stated in different ways. For

example, consider an amusement park that brought in $3100 in revenue by charging

$9.00 for adults and $5.00 for children, while selling 500 tickets. Using a for adult and

c for children, we could write one equation modeling the number of tickets sold:

, and a second modeling the amount of revenue brought in:

. To show that we’re considering both equations simultaneously, a

large “left brace” is used and the result is called a system of two equations in two

variables:

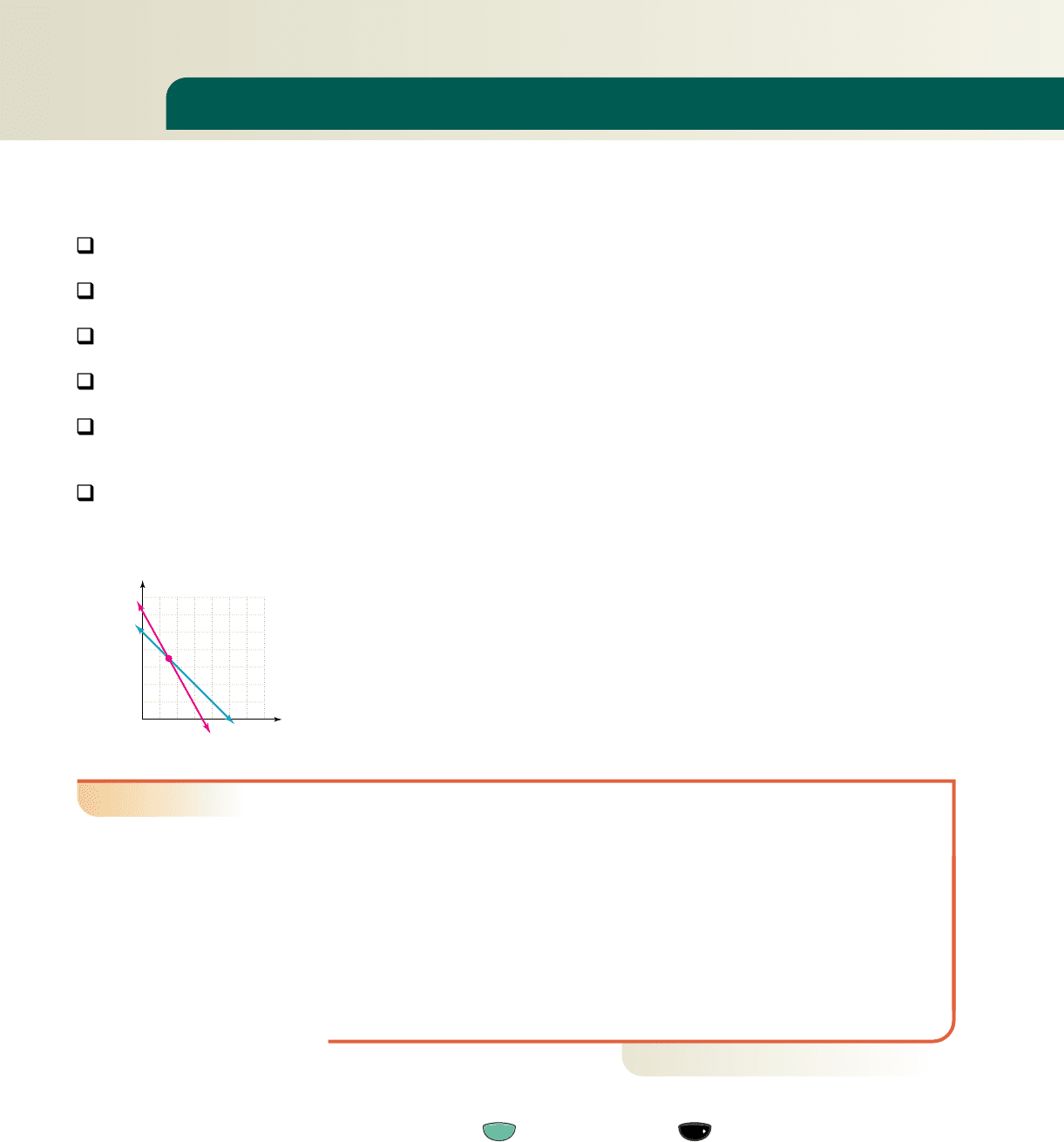
We note that both equations are linear and will have different slope values, so their

graphs must intersect at some point. Since every point on a line satisﬁes the equation

of that line, this point of intersection must satisfy both equations simultaneously and is

the solution to the system. The ﬁgure that accompanies Example 1 shows the point of

intersecion for this system is (150, 350).

EXAMPLE 1

䊳

Verifying Solutions to a System

Verify that (150, 350) is a solution to

Solution

䊳

Substitute the 150 for a and 350 for c in each equation.

ﬁrst equation second equation

✓✓

Since (150, 350) satisﬁes both equations, it is the solution to the system and we

ﬁnd the park sold 150 adult tickets and 350 tickets for children.

Now try Exercises 7 through 18

䊳

To check the solution to Example 1 on a graphing calculator, recall that we can store

values in any of the characters using the key. The home screen shown in

Figure 6.1 shows that we’ve stored a value of 150 in alpha location A, and 350 in loca-

tion C. The solution to a system can then be checked using these alpha keys and the

operations indicated, as shown in Figure 6. 2.

STO

ALPHA

3100  3100 500  500

9 11502 513502 3100 11502 13502 500

9 a  5c  3100 a  c  500

a  c  500

9a  5c  3100

number of tickets

amount of revenue

a  c  500

9a  5c  3100

a  c  500

LEARNING OBJECTIVES

In Section 6.1 you will see

how we can:

A. Verify ordered pair

solutions

B. Solve linear systems by

graphing

C. Solve linear systems by

substitution

D. Solve linear systems by

elimination

E. Recognize inconsistent

systems and dependent

systems

F. Use a system of

equations to model and

solve applications

100

100 300 500 700

300

500

700

Children

Adults

9a  5c  3100

a  c  500

(150, 350)

cob19545_ch06_575-591.qxd 10/5/10 1:14 PM Page 576

B. Solving Systems Graphically

To solve a system of equations means we apply various methods in an attempt to ﬁnd

ordered pair solutions. As Example 1 suggests, one method for ﬁnding solutions is to

graph the system.Any method for graphing the lines can be employed, but to keep im-

portant concepts fresh, the slope-intercept method is used here.

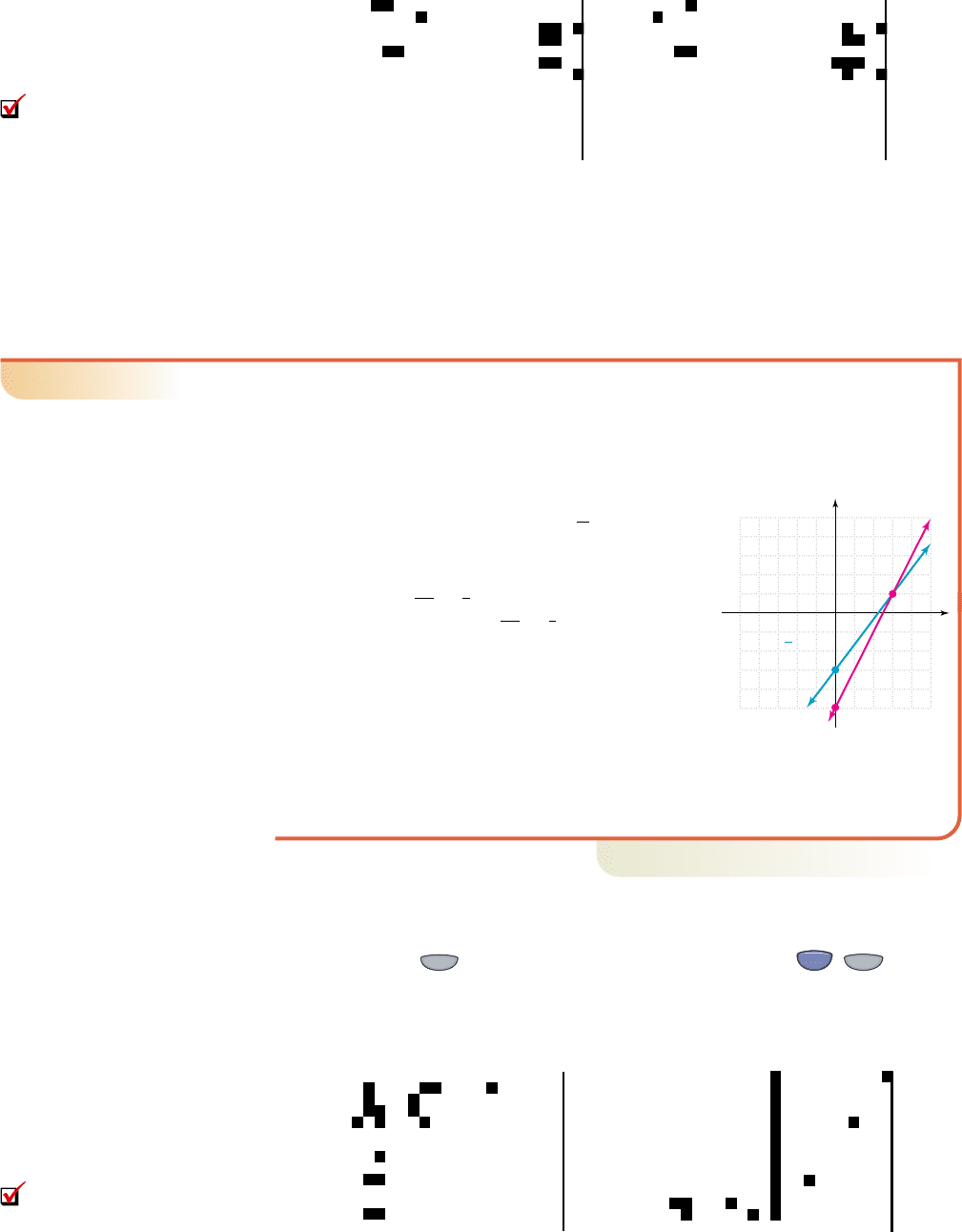
EXAMPLE 2

䊳

Solving a System Graphically

Solve the system by graphing: .

Solution

䊳

First write each equation in slope-intercept form (solve for y):

For the ﬁrst line, with y-intercept

The second equation yields with as

the y-intercept. Both are then graphed on the grid as

shown. The point of intersection appears to be (3, 1),

and checking this point in both equations gives

substitute 3

✓

for

and 1 for

✓

This veriﬁes that (3, 1) is the solution to the system.

Now try Exercises 19 through 22

䊳

Graphical solutions to a system of equations can be found using a graphing calculator

and the intersection-of-graphs method seen earlier. After solving for y and entering the

equations on the screen (Figure 6.3), use the keystrokes (CALC)

5:Intersect to determine the point of intersection, if it exists (Figure 6.4).

TRACE

2nd

⫺5 ⫽⫺5 9 ⫽ 9

⫺2132⫹ 112⫽⫺5 4 132⫺ 3112⫽ 9

⫺2x ⫹ y ⫽⫺5 4 x ⫺ 3y ⫽ 9

10, ⫺52

¢y

¢x

⫽

10, ⫺32.

¢y

¢x

⫽

•

4x ⫺ 3y ⫽ 9

⫺2x ⫹ y ⫽⫺5

•

y ⫽

x ⫺ 3

y ⫽ 2x ⫺ 5

4x ⫺ 3y ⫽ 9

⫺2x ⫹ y ⫽⫺5

6–3 Section 6.1 Linear Systems in Two Variables with Applications 577

College Algebra G&M—

A. You’ve just seen how

we can verify ordered pair

solutions

B. You’ve just seen how

we can solve linear systems by

graphing

Figure 6.1 Figure 6.2

Figure 6.3

⫺55

⫺5

Figure 6.4

5⫺5

⫺5

(3, 1)

(0, ⫺3)

(0, ⫺5)

y ⫽ 2x ⫺ 5

y ⫽ x ⫺ 3

cob19545_ch06_575-591.qxd 10/6/10 7:16 PM Page 577

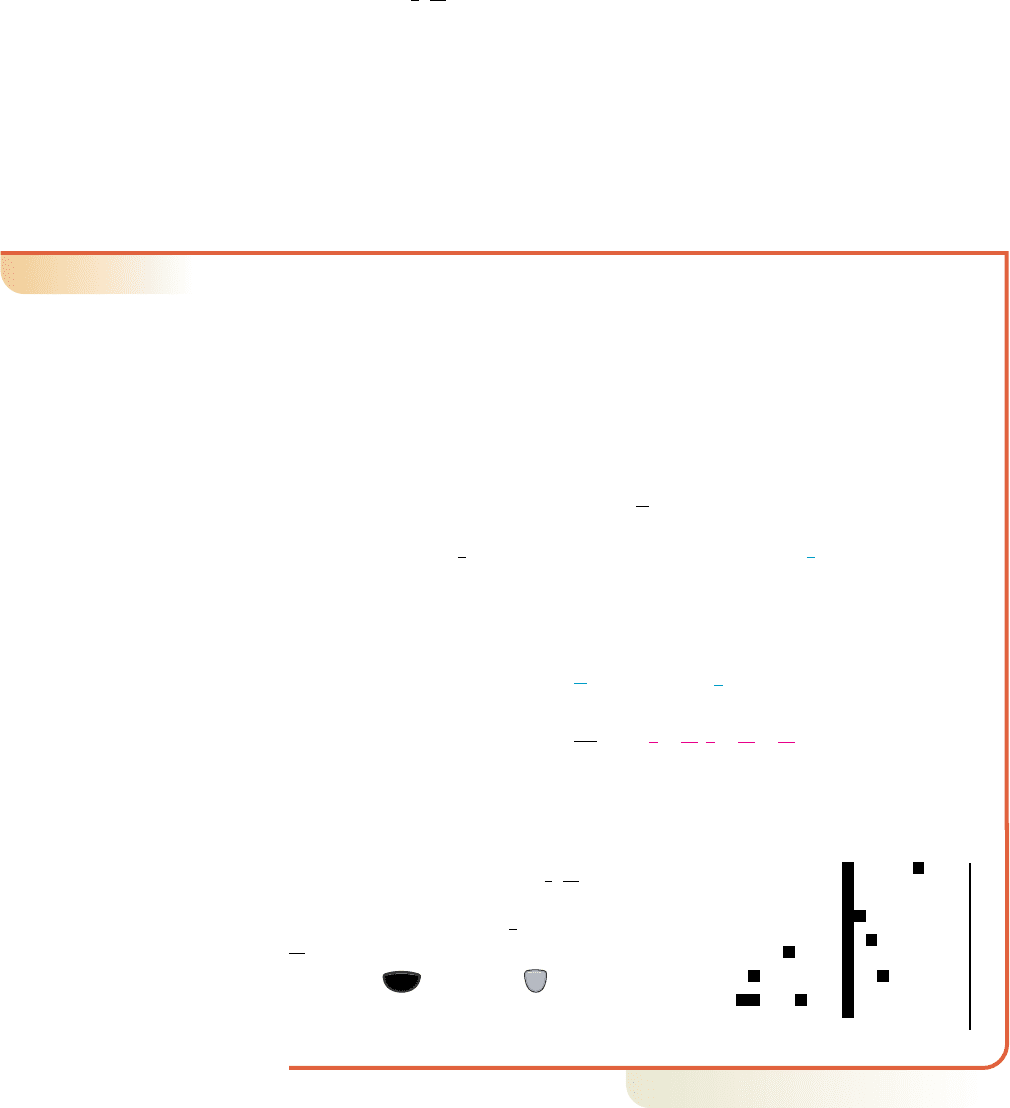
C. Solving Systems by Substitution

While a graphical approach best illustrates why the solution must be an ordered pair, it

does have one obvious drawback—noninteger solutions are difﬁcult to spot. The

ordered pair is the solution to but this would be difﬁcult to

“pinpoint” as a precise location on a hand-drawn graph. To overcome this limitation,

we next consider a method known as substitution. The method involves converting a

system of two equations in two variables into a single equation in one variable by

using an appropriate substitution. For the second equation says “y is two

more than x.” We reason that all points on this line are related this way, including the

point where this line intersects the other. For this reason, we can substitute for y

in the ﬁrst equation, obtaining a single equation in x.

EXAMPLE 3

䊳

Solving a System Using Substitution

Solve using substitution:

Solution

䊳

Since we can replace y with in the ﬁrst equation.

ﬁrst equation

substitute for

simplify

result

The x-coordinate is To ﬁnd the y-coordinate, we substitute for x into either of

the original equations, a process known as back-substitution. Substituting in the

second equation gives

second equation

substitute for

The solution to the system is , which

can be veriﬁed using the intersection-of-

graphs method, and noting and

. See Figure 6.5. Recall that the

keystrokes 1:䉴FRAC can be used to

convert decimal numbers to fractions.

Now try Exercises 23 through 32

䊳

If neither equation allows an immediate substitution, we ﬁrst solve for one of the

variables, either x or y, and then substitute. The method is summarized here, and can

actually be used with either like variables or like variable expressions. See Exer-

cises 33 to 36.

ENTER

MATH

⫽ 2.4

⫽ 0.4

⫽

⫹

⫽

⫹ 2

y ⫽ x ⫹ 2

x ⫽

5 x ⫹ 2 ⫽ 4

x ⫹ 2 4 x ⫹ 1x ⫹ 22⫽ 4

4 x ⫹ y ⫽ 4

x ⫹ 2y ⫽ x ⫹ 2,

4x ⫹ y ⫽ 4

y ⫽ x ⫹ 2

x ⫹ 2

4x ⫹ y ⫽ 4

y ⫽ x ⫹ 2

4x ⫹ y ⫽ 4

y ⫽ x ⫹ 2

578 CHAPTER 6 Systems of Equations and Inequalities 6–4

College Algebra G&M—

55

5

 4X  4, Y

 X  2

Figure 6.5

cob19545_ch06_575-591.qxd 1/8/11 3:28 PM Page 578

Solving Systems Using Substitution

1. Solve one of the equations for x in terms of y or y in terms of x.

2. Substitute for the appropriate variable in the other equation and solve for the

variable that remains.

3. Substitute the value from step 2 into either of the original equations and solve

for the other unknown.

4. Write the answer as an ordered pair and check the solution in both original

equations.

D. Solving Systems Using Elimination

Now consider the system where solving for any one of the

variables will result in fractional values. The substitution method can still be used, but

often the elimination method is more efﬁcient. The method takes its name from what

happens when you add certain equations in a system (by adding the like terms from

each). If the coefﬁcients of either x or y are additive inverses—they sum to zero and

are eliminated. For the system shown, “adding the equations” produces , giving

, then using back-substitution (verify).

If neither of the like-variable terms sum to zero, we can multiply one or both equa-

tions by a nonzero constant to “match up” the coefﬁcients, so an elimination will take

place. In doing so, we create an equivalent system of equations, meaning one that has

the same solution as the original system. For , multiplying the

second equation by 2 produces , and after adding the equations,

we see that . Note the three systems produced are equivalent, and all have (4, 3)

as a solution ( was found using back-substitution).

1. 2. 3.

In summary,

Operations that Produce an Equivalent System

1. Changing the order of the equations.

2. Replacing an equation by a nonzero constant multiple of that equation.

3. Replacing an equation with the sum of two equations from the system.

Before beginning a solution using elimination, check to make sure the equations

are written in the standard form so that like terms will appear

above/below each other. Throughout this chapter, we will use R1 to represent the

equation in row 1 of the system, R2 to represent the equation in row 2, and so on. These

designations are used to help describe and document the steps being used to solve a

system, as in Example 4 where indicates the ﬁrst equation has been

multiplied by two, with the result added to the second equation.

EXAMPLE 4

䊳

Solving a System by Elimination

Solve using elimination: e

2x  3y  7

6y  5x  4

2R1  R2

Ax  By  C,

7x  4y  16

x  4

7x  4y  16

6x  4y 12

7x  4y  16

3x  2y 6

y  3

x  4

7x  4y  16

6x  4y 12

7x  4y  16

3x  2y 6

x  1y  3

2y  6

2x  5y  13

2x  3y 7

6–5 Section 6.1 Linear Systems in Two Variables with Applications 579

College Algebra G&M—

C. You’ve just seen how

we can solve linear systems by

substitution

cob19545_ch06_575-591.qxd 10/5/10 1:14 PM Page 579