Coburn J.W., Herdlick J.D. College Algebra: Graphs and Models
Подождите немного. Документ загружается.


For some equations, it’s helpful to apply the multiplicative property of absolute
value:
Multiplicative Property of Absolute Value
If A and B represent algebraic expressions,
.
Note that if the property says More generally
the property is applied where A is any constant.
EXAMPLE 3
䊳
Solving Equations Using the Multiplicative Property of Absolute Value
Solve:
Solution
䊳
original equation
subtract 5
apply multiplicative property of absolute value
simplify
divide by 2
apply property of absolute value equations
Both solutions check. The solution set is
Now try Exercises 23 and 24
䊳
In some instances, we have one absolute value quantity equal to another, as in .
From this equation, four possible solutions are immediately apparent:
(1) A B (2) A B (3) A B (4) A B
However, basic properties of equality show that equations (1) and (4) are equivalent, as
are equations (2) and (3), meaning all solutions can be found using only equations (1)
and (2).
EXAMPLE 4
䊳
Solving Absolute Value Equations with Two Absolute Value Expressions
Solve the equation .
Solution
䊳
This equation has the form , where and . From our
previous discussion, all solutions can be found using and .
solution template
substitute
subtract 7
subtract
x
x 8
2 x x 8
2 x 7 x 1
A B
A BA B
B x 1A 2x 7
冟
A
冟
冟
B
冟
冟
2x 7
冟
冟
x 1
冟
冟
A
冟
冟
B
冟
54, 46.
x 4
or
x 4
冟
x
冟
4
2
冟
x
冟
8
冟
2
冟冟
x
冟
8
冟
2x
冟
8
冟
2x
冟
5 13
冟
2x
冟
5 13.
冟
1
#
B
冟
冟
1
冟
冟
B
冟
冟
B
冟
.A 1
then
冟
AB
冟
冟
A
冟冟
B
冟
220 CHAPTER 2 More on Functions 2–34
College Algebra G&M—
solution template
substitute
distribute
add
x
, subtract 7
divide by 3 x 2
3 x 6
2 x 7 x 1
2 x 7 1x 12
A B
The solutions are and . Verify the solutions by substituting them
into the original equation.
Now try Exercises 25 and 26
䊳
x 2x 8
A. You’ve just seen how
we can solve absolute value
equations
cob19545_ch02_218-229.qxd 11/1/10 8:11 AM Page 220

2–35 Section 2.3 Absolute Value Functions, Equations, and Inequalities 221
College Algebra G&M—
B. Solving “Less Than” Absolute Value Inequalities
Absolute value inequalities can be solved using the basic concept underlying the
property of absolute value equalities. Whereas the equation asks for all numbers
x whose distance from zero is equal to 4, the inequality asks for all numbers x
whose distance from zero is less than 4.
冟
x
冟
6 4
冟
x
冟
4
0
Distance from zero is less than 4
)
)
1 2 345
⫺5 ⫺4 ⫺3 ⫺2 ⫺1
As Figure 2.42 illustrates, the solutions are and , which can be written
as the joint inequality This idea can likewise be extended to include
the absolute value of an algebraic expression X as follows.
Property I: Absolute Value Inequalities (Less Than)
If X represents an algebraic expression and k is a positive real number,
Property I can also be applied when the “ ” symbol is used. Also notice that if
, the solution is the empty set since the absolute value of any quantity is always
positive or zero.
EXAMPLE 5
䊳
Solving “Less Than” Absolute Value Inequalities
Solve the inequalities:
a. b.
Solution
䊳
a. original inequality
multiply by 4
apply Property I
subtract 2 from all three parts
divide all three parts by 3
The solution interval is
b.
original inequality
Since the absolute value of any quantity is always positive or zero, the solution
for this inequality is the empty set: { }.
Now try Exercises 27 through 38
䊳
As with the inequalities from Section 1.5, solutions to absolute value inequalities
can be checked using a test value. For Example 5(a), substituting from the
solution interval yields:
✓
1
2
1
x 0
冟
2x 7
冟
6 5
32,
2
3
4.
2 x
2
3
6 3x 2
4 3x 2 4
冟
3x 2
冟
4
冟
3x 2
冟
4
1
冟
2x 7
冟
6 5
冟
3x 2
冟
4
1
k 6 0
implies k 6 X 6 k
then
冟
X
冟
6 k
4 6 x 6 4.
x 6 4x 7 4
Figure 2.42
cob19545_ch02_218-229.qxd 11/1/10 8:11 AM Page 221

In addition to checking absolute value inequalities using a test value, the TABLE
feature of a graphing calculator can be used, alone or in conjunction with a relational
test. Relational tests have the calculator return a “1” if a given statement is true, and a
“0” otherwise. To illustrate, consider the inequality . Enter the
expression on the left as Y
1
, recalling the “abs(” notation is accessed in the menu:
(NUM) “1:abs(” (note this option gives only the left parenthesis, you must
supply the right). We can then simply inspect the Y
1
column of the TABLE to find out-
puts that are less than or equal to 5. To use a relational test, we enter as Y
2
(Figure 2.43), with the “less than or equal to” symbol accessed using .
Now the calculator will automatically check the truth of the statement for any value of x
(but note we are only checking integer values), and display the result in the Y
2
column
of the TABLE (Figure 2.44). After scrolling through the table, both approaches
show that for [1, 5].
C. Solving “Greater Than” Absolute Value Inequalities
For “greater than” inequalities, consider Now we’re asked to find all numbers
x whose distance from zero is greater than 4. As Figure 2.45 shows, solutions are
found in the interval to the left of or to the right of 4. The fact the intervals are
disjoint (disconnected) is reflected in this graph, in the inequalities or
as well as the interval notation
As before, we can extend this idea to include algebraic expressions, as follows:
Property II: Absolute Value Inequalities (Greater Than)
If X represents an algebraic expression and k is a positive real number,
EXAMPLE 6
䊳
Solving “Greater Than” Absolute Value Inequalities
Solve the inequalities:
a. b.
冟
5x 2
冟
3
2
1
3
`3
x
2
` 6 2
implies X 6 k
or
X 7 k
then
冟
X
冟
7 k
0
Distance from zero
is greater than 4
Distance from zero
is greater than 4
)
)
1 2 34 76
5
⫺7 ⫺6 ⫺5 ⫺4 ⫺3 ⫺2 ⫺1
x 僆 1q, 42 ´ 14, q2.
x 7 4,x 6 4
4,
冟
x
冟
7 4.
Figure 2.43 Figure 2.44
x 僆2
冟
x 3
冟
1 5
6:ⱕ
MATH
2nd
Y
1
5
ENTER
MATH
MATH
2
冟
x 3
冟
1 5
222 CHAPTER 2 More on Functions 2–36
College Algebra G&M—
B. You’ve just seen how
we can solve “less than”
absolute value inequalities
Figure 2.45
cob19545_ch02_218-229.qxd 11/1/10 8:11 AM Page 222

Solution
䊳
a. Note the exercise is given as a less than inequality, but as we multiply both
sides by we must reverse the inequality symbol.
original inequality
multiply by ⴚ3,
reverse the symbol
apply Property II
subtract 3
multiply by 2
Property II yields the disjoint intervals as the solution.
b.
original inequality
Since the absolute value of any quantity is always positive or zero, the solution
for this inequality is all real numbers:
Now try Exercises 39 through 54
䊳
A calculator check is shown for part (a) in Figures 2.46 through 2.48.
This helps to verify the solution interval is .
Due to the nature of absolute value functions, there are times when an absolute
value relation cannot be satisfied. For instance the equation has no solu-
tions, as the left-hand expression will always represent a non-negative value. The in-
equality has no solutions for the same reason. On the other hand, the
inequality is true for all real numbers, since any value substituted for x will
result in a nonnegative value. We can generalize many of these special cases as follows.
Absolute Value Functions—Special Cases
Given k is a positive real number and A represents an algebraic expression,
has no solutions has no solutions is true for all
real numbers
See Exercises 51 through 54.
CAUTION
䊳
Be sure you note the difference between the individual solutions of an absolute value
equation, and the solution intervals that often result from solving absolute value inequali-
ties. The solution indicates that both and are solutions, while the so-
lution indicates that all numbers between and 5, including are solutions.2,232, 52
x 5x 252, 56
冟
A
冟
7 k
冟
A
冟
6 k
冟
A
冟
k
冟
9 x
冟
0
冟
2x 3
冟
6 1
冟
x 4
冟
2
x 僆 1q, 182 ´ 16, q2
x 僆 ⺢.
冟
5x 2
冟
3
2
x 僆 1q, 182 ´ 16, q2
x 6 18
or
x 7 6
x
2
6 9
or
x
2
7 3
3
x
2
6 6
or
3
x
2
7 6
`3
x
2
` 7 6
1
3
`3
x
2
` 6 2
3,
2–37 Section 2.3 Absolute Value Functions, Equations, and Inequalities 223
College Algebra G&M—
Figure 2.46 Figure 2.47 Figure 2.48
0
)
)
6 12 18 24 30
⫺30 ⫺24 ⫺18 ⫺12 ⫺6
C. You’ve just seen how
we can solve “greater than”
absolute value inequalities
cob19545_ch02_218-229.qxd 11/23/10 8:17 AM Page 223

below the other (inequalities). For , enter the expression
as Y
1
on the screen, and as Y
2
. Using 4:ZDecimal
produces the graph shown in Figure 2.49. Using (CALC) 5:intersect, we
find the graphs intersect at and (Figure 2.50), and the graph of Y
1
is
above the graph of Y
2
in this interval. Since this is a “less than” inequality, the solutions
are outside of this interval, which gives as the solution
interval. Note that the zeroes/x-intercept method could also have been used.
EXAMPLE 7
䊳
Solving Absolute Equations and Inequalities Graphically
For and , solve
a. b. c.
Solution
䊳
a. With as Y
1
and
as Y
2
(set to graph in bold),
using (CALC) 5:intersect
shows the graphs intersect at
and (see figure). These are
the solutions to .
b. The graph of Y
1
is below the graph of Y
2
between these points of
intersection, so the solution interval for is [0, 5].
c. The graph of Y
1
is above the graph of Y
2
outside this interval,
giving a solution of for .
Now try Exercises 55 through 58
䊳
E. Applications Involving Absolute Value
Applications of absolute value often involve finding a range of values for which a given
statement is true. Many times, the equation or inequality used must be modeled after
a given description or from given information, as in Example 8.
2.5
冟
x 2
冟
8 7
1
2
x 3x 僆 1q, 02 ´ 15, q2
1Y
1
7 Y
2
2
x 僆2.5
冟
x 2
冟
8
1
2
x 3
1Y
1
6 Y
2
2
2.5
冟
x 2
冟
8
1
2
x 3
x 5x 0
1Y
1
Y
2
2
TRACE
2nd
g1x2
1
2
x 3
f 1x2 2.5
冟
x 2
冟
8
f
1x27 g1x2f 1x2 g1x2f 1x2 g1x2
g1x2
1
2
x 3f 1x2 2.5
冟
x 2
冟
8
x 僆 1q, 1.52 ´ 13.5, q2
x 3.5x 1.5
TRACE
2nd
ZOOM
2
Y=
2
冟
X 1
冟
3
2
冟
x 1
冟
3 6 2
224 CHAPTER 2 More on Functions 2–38
College Algebra G&M—
4.7
3.1
3.1
4.7
4.7
3.1
3.1
4.7
10
10
10
10
D. You’ve just seen how
we can solve absolute value
equations and inequalities
graphically
D. Solving Absolute Value Equations
and Inequalities Graphically
The concepts studied in Section 1.5 (solving linear equations and inequalities
graphically) are easily extended to other kinds of relations. Essentially, we treat
each expression forming the equation or inequality as a separate function, then graph
both functions to find points of intersection (equations) or where one graph is above or
Figure 2.49 Figure 2.50
cob19545_ch02_218-229.qxd 11/1/10 8:12 AM Page 224

EXAMPLE 8
䊳
Solving Applications Involving Absolute Value Inequalities
For new cars, the number of miles per gallon (mpg) a car will get is heavily
dependent on whether it is used mainly for short trips and city driving, or primarily
on the highway for longer trips. For a certain car, the number of miles per gallon
that a driver can expect varies by no more than 6.5 mpg above or below its field
tested average of 28.4 mpg. What range of mileage values can a driver expect
for this car?
Solution
䊳
Field tested average: 28.4 mpg gather information
mileage varies by no more than 6.5 mpg highlight key phrases
make the problem visual
Let m represent the miles per gallon a driver can expect. assign a variable
Then the difference between m and 28.4 can be no more
than 6.5, or
write an equation model
equation model
apply Property I
add 28.4 to all three parts
The mileage that a driver can expect ranges from a low of 21.9 mpg
to a high of 34.9 mpg.
Now try Exercises 61 through 70
䊳
21.9 m 34.9
6.5 m 28.4 6.5
冟
m 28.4
冟
6.5
冟
m 28.4
冟
6.5.
28.4
⫺6.5 ⫹6.5
2–39 Section 2.3 Absolute Value Functions, Equations, and Inequalities 225
College Algebra G&M—
E. You’ve just seen how
we can solve applications
involving absolute value
2.3 EXERCISES
䊳
CONCEPTS AND VOCABULARY
Fill in the blank with the appropriate word or phrase. Carefully reread the section if needed.
1. When multiplying or dividing by a negative
quantity, we the inequality symbol to
maintain a true statement.
2. To write an absolute value equation or inequality in
simplified form, we the absolute value
expression on one side.
3. The absolute value equation is true
when or when .
2x 3 2x 3
冟
2x 3
冟
7 4. The absolute value inequality is
true when and .3x 6 63x 6 7
冟
3x 6
冟
6 12
Describe the solution set for each inequality (assume k > 0). Justify your answer.
5.
冟
ax b
冟
6 k 6.
冟
ax b
冟
7 k
cob19545_ch02_218-229.qxd 11/23/10 8:18 AM Page 225

226 CHAPTER 2 More on Functions 2–40
College Algebra G&M—
䊳
DEVELOPING YOUR SKILLS
Solve each absolute value equation. Write the solution in
set notation. For Exercises 7 to 18, verify solutions by
substituting into the original equation. For Exercises
19–26 verify solutions using a calculator.
7.
8.
9.
10.
11.
12.
13.
14.
15.
16.
17.
18.
19.
20.
21.
22.
23.
24.
25.
26.
Solve each absolute value inequality. Write solutions in
interval notation. Check solutions by back substitution,
or using a calculator.
27.
28.
29.
30.
31.
32.
33.
34.
冟
2 3u
冟
5 4
冟
4 3z
冟
12 6 7
冟
2c 3
冟
5 6 1
冟
3b 11
冟
6 9
2
冟
n
冟
3 7 7
3
冟
m
冟
2 7 4
5
冟
q 2
冟
7 8
3
冟
p 4
冟
5 6 8
冟
2x 1
冟
冟
x 3
冟
冟
x 2
冟
冟
3x 4
冟
5.3
冟
1.25n
冟
6.7 43.8
8.7
冟
2.5x
冟
26.6 8.2
5.3
冟
q 9.2
冟
6.7 43.8
8.7
冟
p 7.5
冟
26.6 8.2
2 `3
v
3
` 1 5
3 `
w
2
4 ` 1 4
5
冟
2y
冟
14 6
2
冟
3x
冟
17 5
3
冟
c
冟
5 6
2
冟
b
冟
3 4
冟
3q 4
冟
3 5
冟
7p 3
冟
6 5
7
冟
2w 5
冟
6.3 11.2
2
冟
4v 5
冟
6.5 10.3
2
冟
y 3
冟
4 14
3
冟
x 5
冟
6 15
3
冟
n 5
冟
14 2
2
冟
m 1
冟
7 3
35.
36.
37.
38.
39.
40.
41.
42.
43.
44.
45.
46.
47.
48.
49.
50.
51.
52.
53.
54.
Use the intersect command on a graphing calculator
and the given functions to solve (a) ,
(b) , and (c) .
55. ,
56. ,
57. ,
58. f
1x2 2
冟
x 3
冟
2, g1x2
冟
x 4
冟
6
g1x22
冟
x 1
冟
5f
1x2 0.5
冟
x 3
冟
1
g1x2
3
2
x 9f 1x2
冟
x 2
冟
1
g1x2
1
2
x 2f 1x2
冟
x 3
冟
2
f 1x26 g1x2f 1x2 g1x2
f 1x2 g1x2
冟
5u 3
冟
8 7 6
冟
4z 9
冟
6 4
0.9
冟
2p 7
冟
16.11 10.89
3.9
冟
4q 5
冟
8.7 22.5
3
冟
7 2k
冟
11 7 10
4
冟
5 2h
冟
9 7 11
4 `
5
4
2n `
3
4
2 6 `3m
4
5
`
1
5
5
冟
2c 7
冟
1 11
3
冟
5 7d
冟
9 15
冟
p
冟
5
3
2
9
4
冟
q
冟
2
5
6
1
3
5
冟
v
冟
3 23
2
冟
w
冟
5 11
冟
m 1
冟
7 5
冟
n 3
冟
7 7
15
16
`
2y 3
4
3
8
`
`
4x 5
3
1
2
`
7
6
冟
3w 2
冟
2
6 6 8
冟
5v 1
冟
4
8 6 9
cob19545_ch02_218-229.qxd 11/23/10 8:18 AM Page 226

2–41 Section 2.3 Absolute Value Functions, Equations, and Inequalities 227
College Algebra G&M—
䊳
WORKING WITH FORMULAS
59. Spring Oscillation:
A weight attached to a spring hangs at rest a distance
of x in. off the ground. If the weight is pulled down
(stretched) a distance of L inches and released, the
weight begins to bounce and its distance d off the
ground must satisfy the indicated formula. (a) If x
equals 4 ft and the spring is stretched 3 in. and
released, solve the inequality to find what distances
from the ground the weight will oscillate between.
(b) Solve for x in terms of L and d.
冟
d x
冟
L
60. A “Fair” Coin:
If we flipped a coin 100 times, we expect “heads” to
come up about 50 times if the coin is “fair.” In a study
of probability, it can be shown that the number of
heads h that appears in such an experiment should
satisfy the given inequality to be considered “fair.”
(a) Solve this inequality for h. (b) If you flipped a
coin 100 times and obtained 40 heads, is the coin
“fair”?
`
h 50
5
` 6 1.645
䊳
APPLICATIONS
Solve each application of absolute value.
61. Altitude of jet stream: To take advantage of the jet
stream, an airplane must fly at a height h (in feet)
that satisfies the inequality .
Solve the inequality and determine if an altitude of
34,000 ft will place the plane in the jet stream.
62. Quality control tests: In order to satisfy quality
control, the marble columns a company produces
must earn a stress test score S that satisfies the
inequality Solve the inequality
and determine if a score of 17,500 is in the passing
range.
63. Submarine depth: The sonar operator on a
submarine detects an old World War II submarine
net and must decide to detour over or under the
net. The computer gives him a depth model
, where d is the depth in feet
that represents safe passage. At what depth should the
submarine travel to go under or over the net? Answer
using simple inequalities.
64. Optimal fishing depth: When deep-sea fishing,
the optimal depths d (in feet) for catching a
certain type of fish satisfy the inequality
Find the range of depths
that offer the best fishing. Answer using simple
inequalities.
For Exercises 65 through 68, (a) develop a model that
uses an absolute value inequality, and (b) solve.
65. Stock value: My stock in MMM Corporation
fluctuated a great deal in 2009, but never by more
than $3.35 from its current value. If the stock is
worth $37.58 today, what was its range in 2009?
28
冟
d 350
冟
1400 6 0.
20 7 164
冟
d 394
冟
冟
S 17,750
冟
275.
冟
h 35,050
冟
2550
66. Traffic studies: On a
given day, the volume
of traffic at a busy
intersection averages
726 cars per hour
(cph). During rush hour
the volume is much
higher, during “off
hours” much lower.
Find the range of this
volume if it never
varies by more than
235 cph from the
average.
67. Physical training for recruits: For all recruits in the
3rd Armored Battalion, the average number of sit-ups
is 125. For an individual recruit, the amount varies
by no more than 23 sit-ups from the battalion
average. Find the range of sit-ups for this battalion.
68. Computer consultant salaries: The national
average salary for a computer consultant is
$53,336. For a large computer firm, the salaries
offered to their employees vary by no more than
$11,994 from this national average. Find the range
of salaries offered by this company.
69. Tolerances for sport balls:According to the official
rules for golf, baseball, pool, and bowling, (a) golf
balls must be within 0.03 mm of
(b) baseballs must be within 1.01 mm of
(c) billiard balls must be within
0.127 mm of and (d) bowling balls
must be within 12.05 mm of Write
each statement using an absolute value inequality,
then (e) determine which sport gives the least
tolerance t for the diameter
of the ball.
at
width of interval
average value
b
d 2171.05 mm.
d 57.150 mm,
d 73.78 mm,
d 42.7 mm,
cob19545_ch02_218-229.qxd 11/23/10 8:19 AM Page 227

70. Automated packaging: The machines that fill
boxes of breakfast cereal are programmed to fill
each box within a certain tolerance. If the box is
overfilled, the company loses money. If it is
underfilled, it is considered unsuitable for sale.
Suppose that boxes marked “14 ounces” of cereal
must be filled to within 0.1 oz. Find the acceptable
range of weights for this cereal.
228 CHAPTER 2 More on Functions 2–42
College Algebra G&M—
䊳
EXTENDING THE CONCEPT
71. Determine the value or values (if any) that will
make the equation or inequality true.
a. b.
c. d.
e.
72. The equation has only one
solution. Find it and explain why there is only one.
73. In many cases, it can be helpful to view the solutions
to absolute value equations and inequalities as
follows. For any algebraic expression X and positive
冟
5 2x
冟
冟
3 2x
冟
冟
2x 1
冟
x 3
冟
x 3
冟
6xx
冟
x
冟
x
冟
x
冟
冟
x 2
冟
x
2
冟
x
冟
x 8
constant k, the equation has solutions
and , since the absolute value of either
quantity on the left will indeed yield the positive
constant k. Likewise, has solutions
and . Note the inequality symbol has not
been reversed as yet, but will naturally be reversed
as part of the solution process. Solve the following
equations or inequalities using this idea.
a.
b.
c.
d. 3
冟
x 4
冟
7 11
3
冟
x 2
冟
12
冟
x 7
冟
7 4
冟
x 3
冟
5
X 6 k
X 6 k
冟
X
冟
6 k
X k
X k
冟
X
冟
k
䊳
MAINTAINING YOUR SKILLS
74. (R.4) Factor the expression completely:
18x
3
21x
2
60x.
75. (1.5) Solve for (physics).V
2
2W
CA
76. (R.7) Simplify by rationalizing the
denominator. State the result in exact form and
approximate form (to hundredths).
1
3 23
77. (R.3) Solve the inequality, then write the solution
set in interval notation:
312x 527 21x 12 7.
1. Determine whether the following function is even,
odd, or neither.
2. Use a graphing calculator to find the maximum and
minimum values of
. Round to
the nearest hundredth.
3. Use interval notation to identify the interval(s)
where the function from Exercise 2 is increasing,
decreasing, or constant. Round to the nearest
hundredth.
f
1x21.91x
4
2.3x
3
2.2x 5.12
f
1x2 x
2
冟
x
冟
4x
4. Write the equation of the function that has the same
graph of , shifted left 4 units and up 2
units.
5. For the graph given, (a) identify
the function family, (b) describe
or identify the end-behavior,
inflection point, and x- and
y-intercepts, (c) determine
the domain and range, and
(d) determine the value of k if
. Assume required
features have integer values.
f
1k2 2.5
f
1x2 2x
Exercise 5
5⫺5
⫺5
5
x
y
f(x)
MID-CHAPTER CHECK
cob19545_ch02_218-229.qxd 11/23/10 8:19 AM Page 228
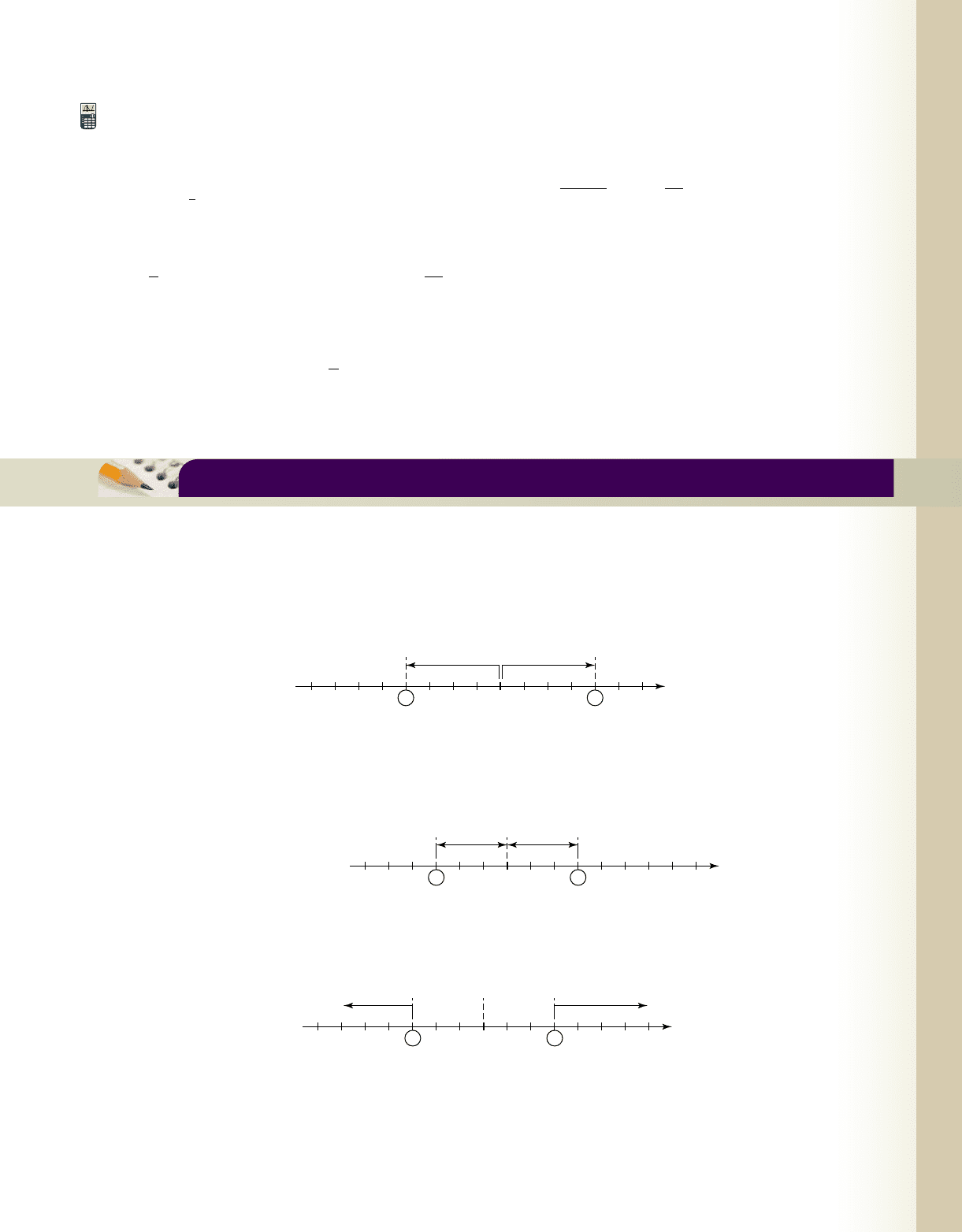
6. Use a graphing calculator to graph the given
functions in the same window and comment on
what you observe.
7
. Solve the following absolute value equations. Write
the solution in set notation.
a. b.
8. Solve the following absolute value inequalities.
Write solutions in interval notation.
a. b. `
x
3
2 ` 5 53
冟
q 4
冟
2 6 10
5
冟
s 3
冟
11
2
2
3
冟
d 5
冟
1 7
r1x2
1
2
1x 32
2
q1x21x 32
2
p1x2 1x 32
2
2–43 Reinforcing Basic Concepts 229
College Algebra G&M—
9. Solve the following absolute value inequalities.
Write solutions in interval notation.
a.
b.
c.
10. Kiteboarding: With the correct sized kite, a person
can kiteboard when the wind is blowing at a speed
w (in mph) that satisfies the inequality
Solve the inequality and determine if a person can
kiteboard with a windspeed of (a) 5 mph?
(b) 12 mph?
冟
w 17
冟
9.
5
冟
k 2
冟
3 6 4
冟
1 y
冟
3
2 7
11
2
3.1
冟
d 2
冟
1.1 7.3
REINFORCING BASIC CONCEPTS
Using Distance to Understand Absolute Value Equations and Inequalities
For any two numbers a and b on the number line, the distance between a and b can be written or In exactly
the same way, the equation can be read, “the distance between 3 and an unknown number is equal to 4.”
The advantage of reading it in this way (instead of “the absolute value of x minus 3 is 4”), is that a much clearer
visualization is formed, giving a constant reminder there are two solutions. In diagram form we have Figure 2.51.
From this we note the solutions are and
In the case of an inequality such as we rewrite the inequality as and read it, “the distance
between and an unknown number is less than or equal to 3.” With some practice, visualizing this relationship
mentally enables a quick statement of the solution: In diagram form we have Figure 2.52.
Equations and inequalities where the coefficient of x is not 1 still lend themselves to this form of conceptual under-
standing. For we read, “the distance between 1 and twice an unknown number is greater than or equal to 3.”
On the number line (Figure 2.53), the number 3 units to the right of 1 is 4, and the number 3 units to the left of 1 is
For and for and the solution set is
Attempt to solve the following equations and inequalities by visualizing a number line. Check all results algebraically.
Exercise 1: Exercise 2: Exercise 3:
冟
2x 3
冟
5
冟
x 1
冟
4
冟
x 2
冟
5
x 僆 1q, 14 ´ 32, q2.2x 4, x 2,2x 2, x 1,
1
3 units 3 unitsDistance between 1 and
2x is greater than or equal to 3.
Distance between 1 and
2x is greater than or equal to 3
13456234 50 678ⴚ2
2.
冟
2x 1
冟
3
1
3 units 3 unitsDistance between 2
and x is less than or equal to 3.
Distance between 2
and x is less than or equal to 3.
34 12 2345065678
x 僆 35, 14.
2
冟
x 122
冟
3
冟
x 2
冟
3,
x 7.x 1
1
4 units 4 units Distance between
3 and x is 4.
Distance between
3 and x is 4.
⫺2⫺3⫺4⫺5 2 3 4 50 6 7 8 9⫺1
冟
x 3
冟
4
冟
b a
冟
.
冟
a b
冟
Figure 2.51
Figure 2.52
Figure 2.53
cob19545_ch02_218-229.qxd 11/1/10 8:15 AM Page 229
